充分发挥“直观想象”让解题更具韵味
2017-01-23张圣官
新高考·高二数学 2016年7期
张圣官


[编者的话]教育部《普通高中数学课程标准》修订组组长、博士生导师王尚志教授提出中国学生在数学学习中应培养好数学抽象、逻辑推理、数学建模、数学运算、直观想象、数据分析六大核心素养,这期请四位老师和两位同学分别谈谈心中的核心素养。
“直观想象”指的是借助几何直观和空间想象感知事物的形态与变化,利用图形理解和解决数学问题的过程,主要包括:借助空间认识事物的位置关系、形态变化与运动规律;利用图形描述、分析数学问题;建立形与数的联系;构建数学问题的直观模型,探索解决问题的思路,直观想象是发现和提出数学问题、分析和解决数学问题的重要手段,是探索和形成论证思路、进行逻辑推理、构建抽象结构的思维基础。
在数学解题中充分发挥直观想象,可以让解题过程具体、生动、形象,更具韵味,
一、利用图形变换,让解题过程更形象
英国心理学家查得·斯根普认为,几何图形是一种视觉符号,与表象的形成密切相关,因此,图形以及图形的加工、变换能力在培养与发展空间想象能力的过程中起了关键作用,图形的变换一般有三种类型:(1)图形的运动与变式;(2)图形的分解与组合;(3)平面图形与空间图形的对比、类比与转换。
例2给出两块相同的正三角形纸片,要求用其中一块剪拼成一个正三棱锥模型,另一块剪拼成一个正三棱柱模型,使它们的全面积都与原三角形的面积相等。
(1)请设计一种剪拼方法,分别用虚线标示在图中,并作简要说明;
(2)试比较你剪拼的正三棱锥与正三棱柱的体积的大小。
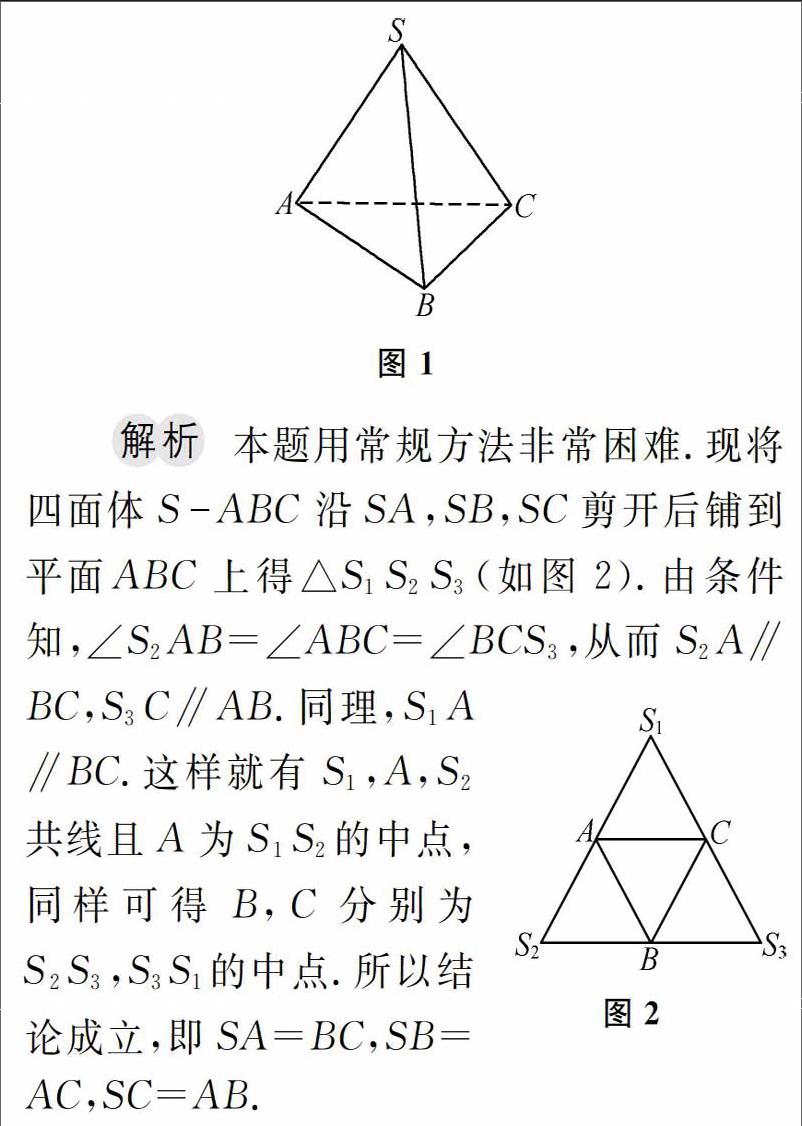
解析(1)如图3,为简化运算,设计正三棱锥为正四面体,设所给正三角形边长为。