一类加法幂等半环簇的自由对象的模型

王丽丽

(重庆理工大学 理学院， 重庆 400054)

设(S,+,·)是(2，2)-型代数,其中“+”和“·”是S上的二元运算。若S满足：① (S，+)和(S，·)都是半群；② (S,+,·)满足等式x(y+z)≈xy+xz和(x+y)z=xz+yz，则称(S,+,·)是半环。 如果一个半环的加法导出半群是一个半格,则称此半环为加法幂等半环[1-6]。

设(S,+,·)是加法幂等半环，对任意的a,b∈(S,+,·)，定义关系a≤b⟺a+b=b，则此关系即是其加法半格上的偏序关系。已知半格的自同态半环是一个加法幂等半环,且每一个ai半环都可以嵌入到某一个半格的自同态半环中。近年来,出现了许多关于加法幂等半环研究的文献[7-12]。众所众知,所有的加法幂等半环形成一个簇,许多的学者对加法幂等半环簇进行了研究,并且得到了许多有趣的结果[2,5,7-11]。同时,一些学者对某些加法幂等半环簇的自由对象进行了刻画,给出了由某些特定等式所确定的加法幂等半环簇的自由对象的模型[6-7,9]。

令S是一个半群， 用P(S) 和Pf(S)分别表示S的所有子集的集合和所有非空子集的集合，在P(S)上定义运算:

A+B=A∪B，AB={ab|a∈A，b∈B}

则P(S) 和Pf(S)在上述运算下形成加法幂等半环。事实上,若X+表示非空集合X上的一个自由半群,则Pf(X+)是加法幂等半环簇中相应于映射k：X→Pf(X+)，x→{x}的自由对象。Zhao等[6]利用半群的闭子半群的概念给出了加法导出是半格的幂等元半环簇中自由对象的模型。令S是一个半群,C是其子半群，称C是S的一个闭子半群，当且仅当对任意的a,b∈S，s,t∈S1，

sat,sbt∈C⟹sabt∈C

A+B=[A∪B]，A∘B=[AB],

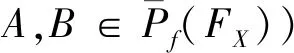
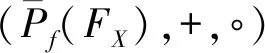
给出下列记号：[n]表示集合{1,2,…,n}；Sg(2,n,1)表示由(x1x2)n≈x1x2定义的半群簇；Sr(2,n,1)表示由(x1x2)n≈x1x2定义的ai-半环簇。

本文引入了半群的(2,n,1)-闭子半群的概念,并利用Sg(2,n,1)的自由对象来构造Sr(2,n,1)的自由对象。 因此,本文的结果推广和丰富了文献 [2，5-6，8-9]中的结果。本文中用到的其他概念和术语,可参考文献[1，3-4]。

1 (2,n,1)-闭子集的概念及性质

令S是一个半群，且M是其子集,则称M为S的(2,n,1)-闭子集,如果：

(∀p,q∈S1,ai1,aj2∈S,i,j=1,2,…,n)pai1aj2q∈M⟹

(∀bsl∈{aml|m=1,2,…,n},s∈[n],l=1,2})

pb11b12b21b22…bn1bn2q∈M

令S是一个半群且A是S的一个子集，容易验证,S的所有包含A的(2,n,1)-闭子集 (至少,S是一个包含A的闭子集) 的交集仍然是S的一个(2,n,1)-闭子集，并且是包含A的S的最小的(2,n,1)-闭子集，称其为由A生成的S的(2,n,1)-闭子集,记作[A]。如果S是一个有限子集,则称[A]是有限生成的。

引理1 令S是一个半群。且A是其子集，定义A(k)(k≥0)如下:

A(0)=A

A(k+1)={pb11b12b21b22…bn1bn2q|p,q∈S1,ai1

aj2∈S,i,j=1,2,…n,pai1aj2q∈A(k)

bsl∈{aml|m=1,2,…,n},s∈[n]

l=1,2}∪A(k)

则对任意的A,B∈P(S),

1)A(0)⊆A(1)⊆…⊆A(k)⊆A(k+1)⊆…;

2) (∀k)A⊆B⟹Ak⊆Bk;

证明

1)是显然的。

2) 令A⊆B。将通过对k用归纳法来证明A(k)⊆B(k)。

当k=0时，因为A(0)=A和B(0)=B,有A(0)⊆B(0)；当k≥0时，假设A(k)⊆B(k)，将要证明A(k+1)⊆B(k+1)。令x∈A(k+1)，需考虑下列2种情况:

①x∈A(k)。 因为A(k)⊆B(k),有x∈B(k)，由B(k)⊆B(k+1)可以推出x∈B(k+1)；

②x=pb11b12b21b22…bn1bn2q,p,q∈S1,ai1,aj2∈S,i,j=1,2,…n,pai1aj2q∈A(k),bsl∈{aml|m=1,2,…,n},s∈[n],l=1,2。因为Ak⊆Bk,有

{pai1aj2q|ai1,aj2∈S,i,j=1,2,…,n}⊆B(k)

因此x=pb11b12b21b22…bn1bn2q∈B(k+1)，从而证明了A(k+1)⊆B(k+1)。

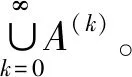
{pai1aj2q|ai1,aj2∈S,i,j=1,2,…,n}⊆A(k0)

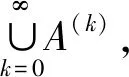
{pai1aj2q|ai1,aj2∈S,i,j=1,2,…,n}⊆M

因为M是(2,n,1)-闭子集，从而可以推出x=pb11b12b21b22…bn1bn2q∈M，证明完毕。

引理2 令S∈Sg(2,n,1)，则对任意的k和A,B,C∈P(S)， 有A⊆B(k)⟹AC⊆(BC)(k)和CA⊆(CB)(k)。

证明由对偶原理,只需要证明对任意的k和任意的A,B,C∈P(S)，A⊆B(k)⟹AC⊆ (BC)(k)。将通过对k归纳来证明这个结论。

1)k=0， 如果A⊆B(0),则A⊆B。进一步,有AC⊆BC，从而推出AC⊆(BC)0。

2)k≥1， 令A⊆B(k)，a∈A,c∈C。 因为a∈B(k),只需要考虑下列情况：

①a∈B(k-1)。 由归纳假设有ac∈(BC)(k-1)，因为(BC)(k-1)⊆(BC)k,得到ac∈(BC)(k)；

②a=pb11b12b21b22…bn1bn2q,p,q∈S1,ai1,aj2∈S,i,j=1,2,…n,pbi1bj2q∈A(k),bsl∈{aml|m=1,2,…,n},s∈[n],l=1,2。显然,{pai1aj2q|ai1,aj2∈S,i,j=1,2,…n}⊆B(k-1)。

由归纳假设有

{pai1aj2qc|ai1,aj2∈S,i,j=1,2,…n}⊆B(k-1)

从而可以得到ac=pb11b12b21b22…bn1bn2qc∈(BC)(k)，因此有ac∈(BC)(k)， 从而有AC⊆(BC)(k)，证明完毕。

令S是一个半群。在Pf(S)定义二元关系ρ如下:

AB∈ρ⟺[A]=[B]

显然,ρ是Pf(S)上的一个等价关系，事实上有：

定理1 令S∈Sg(2,n,1),则ρ是Pf(S)上的一个同余且Pf(S)/ρ∈Sr(2,n,1)。

证明令A,B,C∈P(S)使得(A,B)∈ρ， 要证明ρ是一个半环同余,只要证明(A∪B,B∪C)∈ρ，(AC,BC)∈ρ和(CA,CB)∈ρ。

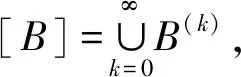
A∪C⊆B(k0)∪C⊆B(k0)∪C(k0)⊆

(B∪C)(k0)⊆[B∪C]

从而[A∪C]⊆[B∪C]。类似地，[B∪C]⊆[A∪C]， 因此[A∪C]=[B∪C],并且(A∪B,B∪C)∈ρ。

2) (AC,BC)∈ρ。类似于 1) 的证明,对某个k0，由引理 2可得(AC)⊆(BC)(k0)。 因为(BC)(k0)⊆[BC],推导出AC⊆[BC],从而[AC]⊆[BC]。类似地,[BC]⊆[AC]，因此[AC]=[BC],从而有(AC,BC)∈ρ。

3) (CA,CB)∈ρ。类似于2)的证明，要证Pf(S)/ρ∈Sr(2,n,1),只需证A1,A2∈Pf(S),((A1A2)n,A1A2)∈ρ,即[(A1A2)n]= [A1A2]。 令bi∈Ai,i=1,2,则

b1b2=(b1b2)n∈(A1A2)n

因此A1A2⊆(A1A2)n,进一步有[A1A2]⊆[(A1A2)n]。

如果x∈(A1A2)n,则存在

ai1,aj2∈S,i,j=1,2,…，n

ai1aj2∈A1A2,bsl∈{aml|m=1,2,…,n}

s∈[n],l=1,2

使得

x=b11b12b21b22…bn1bn2

因为b11b12b21b22…bn1bn2∈(A1A2)(1)⊆[A1A2],所以

x=b11b12b21b22…bn1bn2∈[A1A2]

因此(A1A2)n⊆[A1A2]，并且[(A1A2)n]⊆[A1A2]，得到 [(A1A2)n]=[A1A2]， 证明完毕。

2 满足(x1x2)n=x1x2的ai-半环簇的自由对象

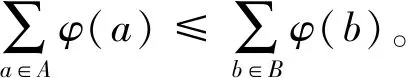
证明将通过对k的归纳来证明这一结果。

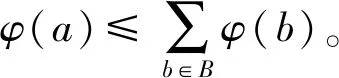
②a=pb11b12b21b22…bn1bn2q,p,q∈S1,ai1,aj2∈S,i,j=1,2,…n,pai1aj2q∈A(k),

bsl∈{aml|m=1,2,…,n},s∈[n],l=1,2

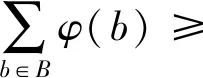
φ(p)(φ(a11)+φ(a12)+…+

φ(a1n))(φ(a21)+φ(a22)+…

+φ(a2n))φ(q)=φ(p)((φ(a11)+

φ(a12)+…+φ(a1n))(φ(a21)+

φ(a22)+…+φ(a2n)))nφ(q)≥

φ(p)φ(b11)φ(b12)φ(b21)φ(b22)…

φ(bn1)φ(bn2)φ(q)≥

φ(pb11b12b21b22…bn1bn2q)=φ(a)

以上是对p,q∈S的情况的证明，p∉S或q∉S的情况可类似证明。证明完毕。

接下来利用Sg(2,n,1)的自由对象来构造Sr(2,n,1)的自由对象，这一结果推广了文献[6]中的定理 3.5。

证明由定理 1 可知Pf(FX)/ρ是Sr(2,n,1)的一个半环， 假设S∈Sr(2,n,1)且λ：X→S是任意一个映射。因为(S,·)∈Sg(2,n,1)且FX是Sg(2,n,1) 的自由对象,则存在唯一的一个φ：FX→(S,·)，使得图1是一个交换图,即φ∘ι=λ。定义一个映射ψ：Pf(FX)/ρ:

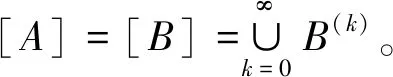
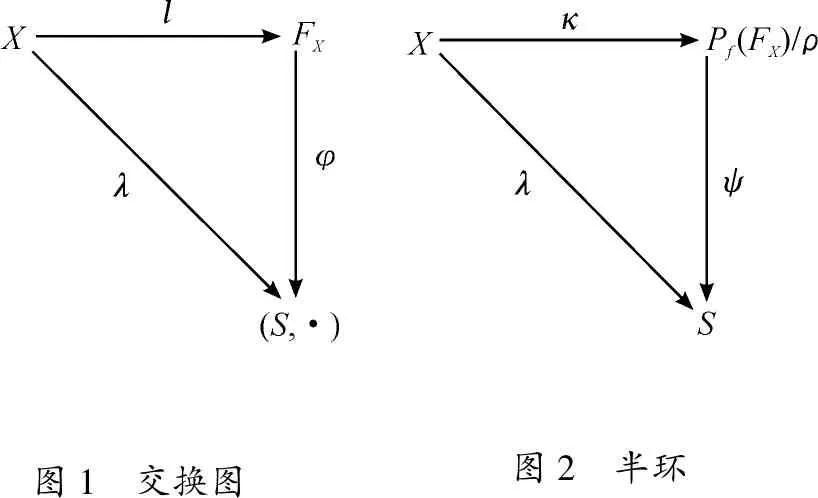
图1 交换图图2 半环

首先,对任意的A,B∈Pf(FX),

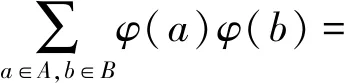
因此ψ是Pf(FX)到S上的半环同态。

其次,选取任意的x∈X,则

(ψ∘κ)(x)=ψ(κ(x))=ψ({ι(x)}ρ)=

ψ(ι(x))=(ψ∘ι)(x)=λ(x)

因而ψ∘κ=λ。

最后,令θ∶Pf(FX)/ρ→S是一个半环同态且使得θ∘κ=λ， 定义一个映射α∶FX→(S,·):

α(a)=θ({a}ρ)(a∈FX)

容易验证α是一个半群同态，并且对任意的x∈X,

(α∘ι)(x)=α(ι(x))=θ({ι(x)}ρ)=

θ(κ(x))=(θ∘κ)(x)=λ(x)

因此α∘ι=λ，由φ的唯一性,有α=φ。 令A∈Pf(FX),则

从而有θ=ψ，证明完毕。

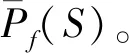
[A]+[B]=[A∪B],[A]∘[B]=

[AB](A,B∈Pf(S))

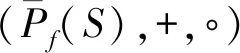
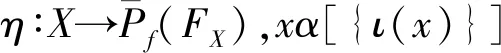
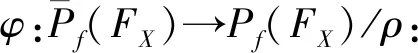
φ([A])=Aρ(A∈Pf(FX))

φ([A])=φ([B])⟺Aρ=Bρ⟺(A,B)∈ρ⟺

[A]=[B]

所以φ的定义是良好的且是一个单设。

另外,φ显然是一个满设且对任意的A,B∈Pf(FX),

φ([A]+[B])=φ([A∪B])=(A∪B)ρ=

Aρ+Bρ=φ([A])+φ([B])

φ([A]∘[B])=φ([AB])=(AB)ρ=

(Aρ)(Bρ)=φ([A])φ([B])