一类具有垂直传播食饵捕食模型的动力学行为

苏 强,赵亚飞，吕贵臣

(重庆理工大学 理学院， 重庆 400054)

20世纪Kermack和Mckendrick[1]提出的传染病仓室模型引起了流行病学家的广泛关注，近年来，传染病动力学的研究进展迅速。经典的方法是在明确某种疾病传播机理的基础上，建立该疾病传播的数学模型，然后对模型进行动力学行为分析，进而给出疾病控制策略。

1 模型的建立及解的有界性

(1)

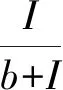
定理1 系统(1)所有满足初值问题的正解是最终一致有界的。

证明令ζ=S+I+Y，沿系统对ζ求导，则

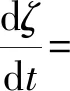
r-d1S-(d2-a)I-d3Y≤r-ηζ

其中η=min{d1,d2-a,d3}，由比较原理[8]可知，存在T>0，当t>T时：

Ω是其最终有界集。

2 非负平衡点的存在性及局部渐近稳定性

通过计算，容易得出系统(1)存在下列非负的平衡点：

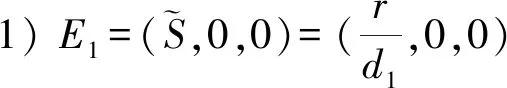
E3=(S*,I*,Y*)

存在，其中：

由于系统是非线性自治系统，可利用Lyapunov稳定性定理间接法[8]结合Routh-Hurwitz判据[9]研究非负平衡点E1、E2、E3的局部渐近稳定。

定理2

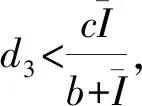
3) 若k1>0，k2>0且k1k2-k3>0，则平衡点E3局部渐近稳定。其中

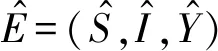
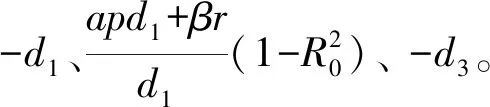
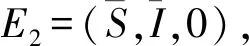
(λ-λ*)f(λ)=0

其中：

由E2的存在性知

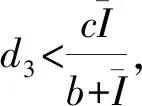
对于平衡点E3=(S*,I*,Y*)，系统(1)的线性近似系统在E3的特征方程为

λ3+k1λ2+k2λ+k3=0

其中：

由Hurwitz判据知，当k1,k2>0，且k1k2-k3>0时，特征方程的所有特征根具有负实部，则平衡点E3局部渐近稳定。

3 Hopf分支和系统的持久性

以下将考虑当内部平衡点E3出现Hopf分支的情况，取感染者死亡率d2作为分支参数。

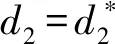
1)k1(d2)k2(d2)-k3(d2)=0;

其中ki(d2)>0(i=1,2,3)。由条件1)直接计算可得：

(ρ1+ρ2-d3ρ3)

(2)

其中:

A1=c(βI*+d1)(b+I*)2

A2=(βI*+d1)(b+I*)2-Y*I*

A3=(β2S*-βa(1-p))(b+I*)3

A4=c-(βI*+d1)(b+I*)

因此式(2)等于零得Hopf分支参数值

接下来考虑条件2)，直接计算可得：

(k3(d2)-k1(d2)k2(d2))′=

因为k1,k2>0，则

为了研究系统(1)的持久性，先引入以下定义和引理。

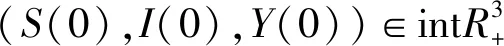
设X为完备度量空间，X0是开集并在X中稠密，X=X0∪∂X0,X0∩∂X0=∅。T(t)为X上的连续半流且满足如下性质：

Tt∘Ts=Tt+s,t,s≥0,T0(x)=x,x∈X

WS(A)=xx∈X,ω(x)≠∅,ω(x)⊂A

引理1[10]假设流T(t)满足以下条件：

1)T(t):X0→X0,∂X0→∂X0；

2) 存在一个t0≥0，使得对t≥t0时，T(t)是紧的；

3)T(t)在X中是点耗散的；

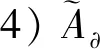
M=M1,M2,…,Mn

则T(t)是一致持久的，当且仅当对任意Mi∈M有WS(E1)∩X0=∅。

通过运用引理1，可以得到系统(1)的一致持久性，见定理4。

证明定义如下集合：

X0=S,I,YS>0,I>0,Y>0

∂X0=S,I,YI=0,Y≥0

显然，X0⊂X,∂X0⊂X,∂X0∩X0=∅。

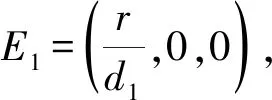
接下来证明WS(E1)∩X0=∅。假设WS(E1)∩X0≠∅，那么存在系统(1)的一个正解(S(t),I(t),Y(t))满足

故存在ε>0和T>0，使得当t>T时，

于是当t>T时，由系统(1)的第2个方程得：

所以，

这与系统(1)解的有界性矛盾，故WS(E1)∩X0=∅。因此由引理1知系统(1)是一致持久的。

4 结束语

本文建立了食饵患病且具有垂直传播带Holling Ⅱ功能反应函数的生态流行病模型，对该模型进行了动力学行为分析，得到了3个平衡点E1、E2、E3局部渐近稳定、内部平衡点E3出现Hopf分支和系统一致持久的充分条件。