一类随机时滞捕食者-食饵模型的定性分析
2019-04-16尹文倩刘桂荣
尹文倩,刘桂荣
(山西大学 数学科学学院, 太原 030006)
随着现代工业和农业的发展,环境污染已成为重要的社会生态问题之一。环境中各种毒素的存在导致许多物种灭绝,这促使很多学者研究毒素对种群的影响[1-4]。
在现实生活中生物会受到环境噪声的影响。为此,建立下列随机时滞捕食者-食饵模型:
(1)

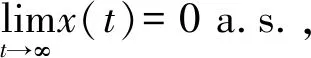
1 主要结论
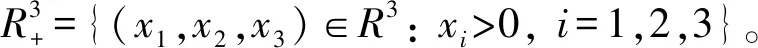
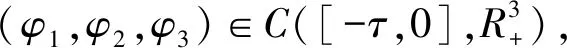
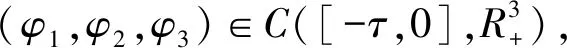
下面采用反证法来证明τ∞=∞ a.s.。若这个结论不成立,则存在常数T>τ和ε∈(0,1)使得P{τ∞≤T}>ε。因此,对任意n≥n0,令Ωn={τn≤T},从而
P{Ωn}≥ε
(2)
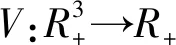
任取n≥n0且0≤t≤(τn∧T),由It公式得
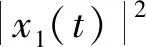
a13(t)x3(t-τ13)]-0.5a21(t)x1(t-τ21)-0.5a31(t)x1(t-τ31)-
a23(t)x3(t-τ23)]+0.5a12(t)x2(t-τ12)+0.5a32(t)x2(t-τ32)-
a32(t)x2(t-τ32)]+0.5a13(t)x3(t-τ13)+0.5a23(t)x3(t-τ23)+
0.5[-r1(t)+r01(t)c01(t)+r2(t)+r02(t)c02(t)+r3(t)+r03(t)c03(t)]+
(3)
其中:
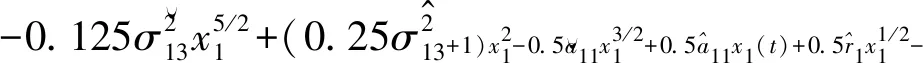
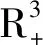
(4)
对式(4)两边同时从0到τn∧T积分并取数学期望得
E[Q(x(τn∧T))+V(x(τn∧T))]≤Q(x(0))+V(x(0))+KE(τn∧T)
由此可得EV(x(τn∧T))≤Q(x(0))+V(x(0))+KT。对n≥n0,由τn的定义可知,对每个ω∈Ωn,存在x(τn,ω)的某个分量xi(τn,ω)等于n或者1/n。结合式(2)可得
(5)
其中IΩn代表Ωn上的示性函数。令n→∞可得,等式(5)的右端等于∞,这与式(5)矛盾。因此τ∞=∞ a.s.,从而模型(1)在[-τ,∞)上存在唯一正解。
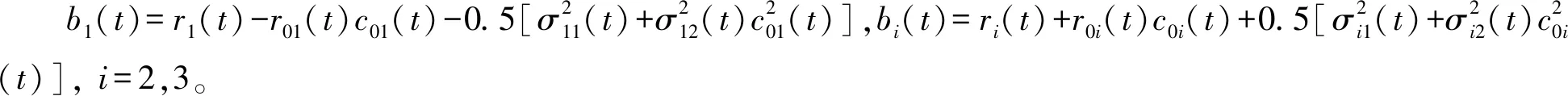
定理2
1) 对于模型(1)中的食饵种群x1,若〈b1(t)〉*<0,种群x1灭绝;若〈b1(t)〉*=0,则种群x1随机非平均持久。
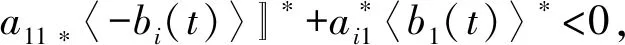
证明
1) 对于lnx1(t)应用It公式[8]并积分得
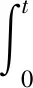
(6)
同理:
(7)
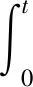
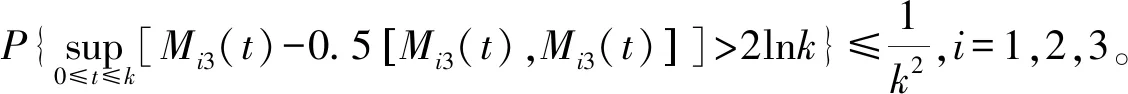
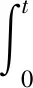
(8)
同理
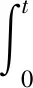
(9)
由此可得,对0 注意到,M1i(t)是初值为M1i(0)=0的连续局部鞅,i=1,2,且 从而 (10) 注意到存在常数T2>T1,使得对于T2≤k-1≤t≤k及k≥k0,都有 (2lnk)/t≤ε/6,M11(t)/t≤ε/6,M12(t)/t≤ε/6 (11) 将其代入式(10)可得 (12) 根据洛必达法则可知 2) 若〈b1(t)〉*≤0,由 1) 知,〈x1(t)〉*=0。注意到〈-bi(t)〉*<0,从而存在充分小的ε>0和T3>0,使得当t>T3时有〈-bi(t)〉<〈-bi(t)〉*+ε<0,i=2,3。由式(7)及式(9)得,对几乎所有的ω∈Ω,存在一个整数值随机变量k0=k0(ω)使得当k≥k0时, t-1lnxi(t)≤t-1lnxi(0)+〈-bi(t)〉+t-1Mi1(t)+t-1Mi2(t)+t-1(2lnk)+ (13) 两边同时取上极限,则由强大数定律得 若〈b1(t)〉*>0时,下面证明结论(2)仍成立。由式(6)及(11)得 t-1lnx1(t)≤t-1lnx1(0)+〈b1(t)〉*+ε/2-(a11*-ε)〈x1(t)+ε/2,t>T2 类似于 1)中情形〈b1(t)〉*=0的证明方法,可得 〈x1(t)〉*≤〈b1(t)〉*/11*a.s. (14) 根据式(7)及(13)知,对几乎所有的ω∈Ω,存在整数值随机变量k0=k0(ω)使得当k≥k0时, t-1lnxi(t)≤t-1lnxi(0)+〈-bi(t)〉+t-1Mi1(t)+t-1Mi2(t)+t-1(2lnk)+ 两边同时取上极限,由强大数定律得 (15) 另一方面,对于固定的ε>0,对几乎所有的ω∈Ω,存在一个整数值随机变量k0=k0(ω),T2>0,使得当k≥k0,t>T4时, 由式(7)及(9)可得,对任意的t>T4有 注:由定理2的证明过程可知,当食饵种群灭绝时,捕食者种群也灭绝。 假设模型(1)的初值为φ1(t)=φ2(t)=φ3(t)=0.3e0.5t,t∈[-τ,0]。为了验证本文的理论结果的合理性,选取下列参数:r1(t)=0.1+0.01sint,r01(t)=0.1+0.01sint,c01(t)=0.4sint,r2(t)=0.1+0.04sint,r02(t)=0.03sint,c02(t)=0.5sint,r3(t)=0.1+0.03sint,r03(t)=0.04sint,c03(t)=0.3×sint,a11(t)=a12(t)=a13(t)=0.3,a21(t)=a22(t)=a23(t)=a31(t)=a32(t)=a33(t)=0.4,τ12=τ13=τ21=τ23=τ31=τ32=1。 图1 种群的数量变化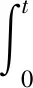
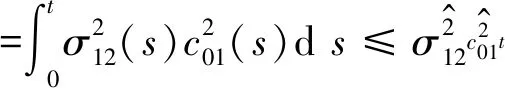
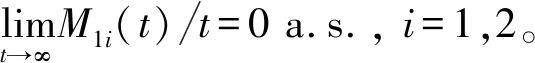
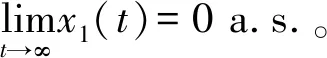

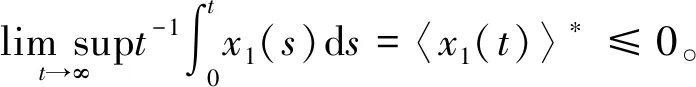
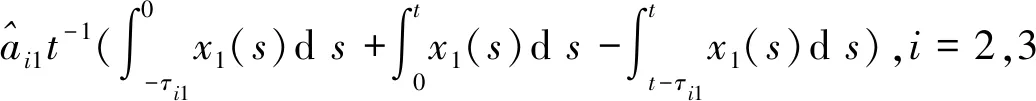

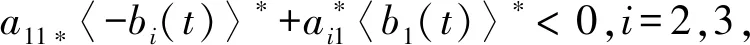
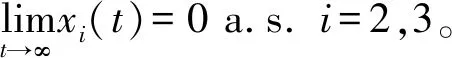
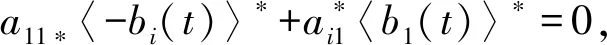
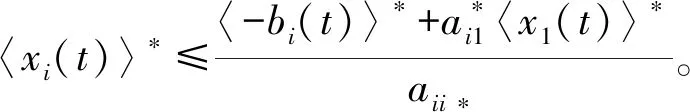
2 数值模拟