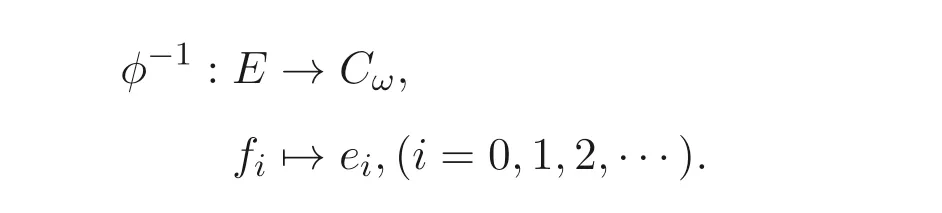关于一致半格的注记

程彦亮, 邵勇

(西北大学数学学院, 陕西 西安 710127)

1 引言

设(S,·) 是交换半群. 若对任意a ∈S有a2=a成立, 则称(S,·) 为半格. 设(S,·)为半格, 在S上定义偏序如下:

由偏序的定义, 对任意a,b ∈S, 易知,ab是a与b的最大下界. 若存在c ∈S,有a ≤c ≤b ⇒c=a或c=b, 则称b覆盖a或a被b覆盖, 记为a ≺b[2]. 设X是偏序集(S,≤) 的非空子集, 若存在a ∈X, 使得对任意x ∈X, 有x ≤a ⇒x=a,则称a为X的极小元. 若存在b ∈X, 使得对任意y ∈X, 有b ≤y ⇒b=y, 则称b为X的极大元. 设(S,·) 为半格, 对任意M ⊆S,M ̸=∅, 若M含有极小元, 则称S满足极小条件. 若M含有极大元, 则称S满足极大条件. 设(S,≤) 为偏序集, 若对任意a,b ∈S,总有a ≤b或b ≤a成立, 则称S为链. 若链满足极小条件, 则称该链为良序链.

定义1.1[1]设E是链, 若对e ∈E, 集合{x ∈E|x

定义1.2[3]设E是半格, 若对任意e ∈E, 有Ee={f ∈E|f ≤e}, 则称Ee为由e生成的主理想.

定义1.3[4]设E是半格, 若对任意e,f ∈E, 有Ee～=Ef, 则称E为一致半格.

若Ee～=Ef ⇒e=f, 则称E为反一致半格.

例1.1设E=Cω={e0,e1,e2,···}, 其中e0>e1>e2>···, 则对任意en ∈Cω,由en生成的主理想为Cωen={en,en+1,en+2,···}. 易知对任意em,en ∈Cω, 其中m,n ∈N={0,1,2,···}, 有Cωem～=Cωen成立. 因此Cω为一致半格.

定义1.4[1]设S是半群, 若对任意a ∈S,a有唯一的逆元, 则称S为逆半群. 若在逆半群S上, 格林D关系为泛关系, 即D=S×S, 则称S为双单逆半群.

由文献[5] 知, 若S是双单逆半群, 则由S的幂等元形成的半格为一致半格, 而半格为一致半格的逆半群并非都是双单逆半群. 例如, 一致半格自身是逆半群, 但是它不是双单逆半群. 但是, 的确存在一个这样的双单逆半群, 即由该一致半格对应的Munn半群. 由文献[1] 知, 不同类型的一致半格所对应的双单逆半群具有不同的结构, 例如,半格同构于Cω的双单逆半群为双单逆ω- 半群. 文献[3] 通过半格之间的一个类型积构造了一致半格M(r). 文献[6] 探究了半格同构于M(r) 的双单逆半群的结构. 显然,Cω是满足极大条件的无限链, 本文探究了满足极大条件的无限链与Cω的关系, 并且给出了满足极大条件的无限链的等价刻画. 讨论了极小条件与一致半格以及极大条件与反一致半格的关系.

若E为半格,E中仅含有一个元素e, 即E={e}, 则称E为平凡半格[7], 易知,平凡半格既是一致的又是反一致的. 下文中所提到的半格, 若无特别说明, 均为至少包含两个元素的非平凡半格.

2 主要结论

引理2.1设E是一致半格, 则E必是无限的.

证明假设E是有限的, 不妨设E={e1,e2,··· ,en},那么存在

因此, 对任意k ∈{1,2,··· ,n}, 有ei ≤ek. 故ei是E的最小元. 进而,Eei={ei}. 然而对任意ej ∈E,(j ̸=i), 则有Eej至少包含两个元素{ei,ej}, 因此|Eej|≥2, 显然,Eei≇Eej,(i ̸=j), 这与E是一致的矛盾, 故E是无限的.

由该引理知, 一致半格必是无限的, 因此在探究极大条件与一致半格的关系时, 仅从无限的角度出发.

引理2.2任何满足极大条件的无限链同构于Cω, 即它是一致半格.

证明设E是满足极大条件的无限链, 则E含有最大元, 记为f0.

通过以下方式定义映射φ:Cω →E.

首先,Cω={e0,e1,e2,···}, 其中e0>e1>e2>···, 令φ将Cω中的最大元映到E中的最大元, 即e0φ=f0.

然后, 由E是无限链知,E {f0} ̸=∅. 又由E满足极大条件知, 存在唯一的f1∈E {f0}, 使得对任意的x1∈E {f0}, 有x1≤f1. 因此, 令φ将e1∈Cω映到E{f0}中的最大元, 即e1φ=f1.

以此类推知,E {f0,f1,··· ,fi−1} ̸=∅. 又由E满足极大条件知, 存在唯一的fi ∈E{f0,f1,··· ,fi−1}, 使得对任意的xi ∈E{f0,f1,··· ,fi−1}, 有xi ≤fi. 因此,令φ将ei ∈Cω映到E{f0,f1,··· ,fi−1}中的最大元, 即eiφ=fi.

综上所述,

容易验证,φ是良定义的, 下证φ是双射:

对于任意ei ̸=ej,(i ̸=j), 有

由E是链知, 当i ̸=j时, 有fi ̸=fj成立, 从而eiφ ̸=ejφ, 故φ是单射.

要证φ是满射. 只需说明以上取法能够取遍E, 即证对于E{f0}中任意元素, 总存在另一元素将其覆盖, 这是因为, 若对任意f ∈E{f0}, 存在唯一元素f′∈E, 使得f ≺f′, 那么f就是集合E{f0,f1,··· ,f′}的最大元, 又由f的任意性知, 以上取法取遍E.

要证对于E{f0}中的任意元素, 总存在另一元素将其覆盖, 由E中元素的任意性知, 只需证对于任意f′∈E, 存在唯一的元素f ∈E, 使得f ≺f′. 假设E中不存在f, 使得f ≺f′成立, 那么集合E{f0,f1,··· ,f′} ⊂E没有最大元. 又由E是无限链知,E{f0,f1,··· ,f′}没有极大元, 且E{f0,f1,··· ,f′}̸=∅. 这与E满足极大条件矛盾, 从而对任意的f′∈E, 存在唯一的f ∈E, 使得f ≺f′.

因此以上取法能够取遍E. 故对于任意的f∗∈E, 总存在k ∈N, 使得fk=f∗, 由于存在ek ∈Cω, 使得ekφ=fk=f∗, 因此φ是满射, 故φ是双射. 下证φ和φ−1都是保序的:

定义

对任意fi,fj ∈E,其中i ̸=j. 不妨设i

由以上引理可知, 若E是满足极大条件的无限链, 那么E是一致半格. 而一致半格并非都是满足极大条件的无限链. 如下例2.1:

例2.1设E是链,并且E的链序同构于整数,即E={··· ,e−2,e−1,e0,e1,e2,···},并且···

证明对于任意em,en ∈E,m,n ∈Z={··· ,−2,−1,0,1,2,···}, 则有

定义映射

容易验证,φ是同构映射, 故Eem～=Een. 因此,E是一致半格.

显然,E是无限链, 但E不满足极大条件, 这是由于E自身没有最大元.E的Hasse 图如图1:

图1

例2.2设E=Cω×Cω, 其中Cω={e0,e1,e2,···},e0>e1>e2>···, 则E是一致半格, 并且满足极大条件, 但E不是无限链.

证明设E=Cω×Cω={em,n|m,n ∈N}, 其中

E的Hasse 图如图2:

图2

对于任意em,n,ep,q ∈E, 则有

类似的,

定义映射

容易验证,φ是双射, 下证φ是同态映射:

对任意er1,s1,er2,s2∈Eem,n, 其中ri,si ∈N,ri ≥m,si ≥n,i=1,2.

从而φ是同构映射, 因此E是一致半格, 显然E有最大元e0.0, 并且E的任意非空子集都含有极大元, 因此E满足极大条件, 但E不是无限链.

以上例子说明, 一致半格不一定为满足极大条件的无限链.

由文献[1] 知, 满足极小条件的反一致半格必为良序链. 由例2.2 表明, 满足极大条件的一致半格未必是无限链.

定理2.1设E是满足极大条件的半格, 则E是无限链当且仅当E是含有幺元的一致半格, 并且每一个主理想都是链.

证明设E是一致半格,|E|≥2. 由引理2.1 知,E是无限的. 由于E含有幺元,并且每一个主理想都是链. 设幺元为e, 则E=Ee, 即E是由e生成的主理想, 故E是无限链.

另一方面, 若E是满足极大条件的无限链, 由引理2.2 知,E是一致半格. 由于E是无限链, 且满足极大条件, 因此,E含有幺元. 显然,E的每一个主理想都是链.

该定理中的任何条件不可缺失, 若E不满足每一个主理想都是链, 则由例2.2 知,E=Cω×Cω,E包含幺元e0,0, 并且E是满足极大条件的一致半格, 易见,E不是无限链.

若E不含有幺元, 设E={e1,e2,e3,e4,...},E的Hasse 图如图3:

图3

由图3 可知,E有3 个极大元, 故E不含有幺元, 显然,E是满足极大条件的一致半格, 并且每一个主理想均为链, 但E不是无限链.

对于定理2.1 而言, 条件“E满足极大条件” 是必要的. 一方面, 若E是含有幺元的一致半格, 并且每一个主理想都是链, 由引理2.1 知,E是无限的, 又由E=Ee知,E是无限链, (e是E的幺元). 另一方面, 若E是无限链, 则E可能是反一致的半格,例如,E是一个链序同构于非负整数的无限链. 即使E包含幺元, 并且每一个主理想都是链,E也未必是一致半格. 如下例:

则E是含有幺元的无限链, 且每一个主理想都是链, 但E不是一致半格.

证明显然, 在(1) 式所定义的偏序下,E是无限链, 从而E的每一个主理想均为链, 又由对于∀(q,m)∈E(q ≥0, m ≥0),

(i) 如果q=0,m ≥0, 那么(q,m)=(0,m)≤(0,0);

(ii) 如果q>0,m ≥0, 那么(q,m)≤(0,0).

因此, (0,0) 是E的幺元, 从而E是含有幺元的无限链, 下证E不是一致的:

假设E是一致的, 则对任意(q,m),(r,n)∈E, 有E(q,m)～=E(r,n), 设φ是E(q,m) 到E(r,n) 的同构映射. 只需取(q,m) = (q,0),(q ̸= 0), (r,n) = (r,rε), 考虑E(q,0) 和E(r,rε),E(q,0) 有最大元(q,0),E(r,rε) 有最大元(r,rε), 由同构映射保序, 故φ将(q,0) 映到(r,rε). 由于集合{x ∈E|x< (r,rε)}没有最大元, 由定义1.1知, (r,rε) 没有紧接后元, 集合{x ∈E|x< (q,0)}(q ̸= 0) 有最大元(q,1), 从而(q,0)有紧接后元, 这与φ是同构映射矛盾, 故E不是一致半格.

经过上述分析, 定理2.1 中的条件缺一不可, 由例2.3 知, 该定理中的条件“E满足极大条件” 是必要的.

在文献[1] 中, 探讨了极小条件与反一致半格的关系, 类似地, 由定理2.1 探究了极大条件与一致半格的关系, 现在继续讨论一致半格与极小条件以及反一致半格与极大条件的关系.

定理2.2E是满足极小条件的一致半格当且仅当E是平凡半格(|E|=1).

证明首先, 若E是平凡半格, 设E={e}, 显然,E是一致的. 由E的非空子集只能是自身, 从而极小元为e, 故E是满足极小条件的一致半格.

另一方面,设E是一致半格,并且满足极小条件.假设E不是平凡半格,即|E|≥2.由于E满足极小条件, 从而E包含唯一的极小元e, 这是因为, 假设E包含两个不同的极小元e,f, 则有ef ≤e,ef ≤f, 由于e,f都是极小元, 从而ef=e,ef=f,故e=f. 因此,E包含唯一的极小元e. 进而, 由e生成的主理想Ee={e}. 由E不是平凡半格, 故存在f ∈E,f ̸=e, 则由f生成的主理想Ef至少包含两个元素{e,f},从而Ee≇Ef. 这与E是一致半格矛盾, 故E必为平凡半格.

由文献[1] 知, 设E是有限半格, 若E为链, 则E必是反一致的. 接下来探究E是非链的情况.

引理2.3若E是非链的有限半格, 则E既不是一致的也不是反一致的.

证明设E是非链有限半格, 由引理2.1 知, 非平凡一致半格一定是无限的, 故E不是一致的. 下证E不是反一致的:

假设E是反一致的, 由于E是有限半格, 故E满足极小条件, 因此,E是满足极小条件的反一致半格, 则E是良序链, 这与E是非链的矛盾. 因此E不是反一致的.

定理2.3若E是满足极大条件的反一致半格, 则

证明若|E|< +∞, 即E是有限半格, 假设E不是链, 即E是非链的有限半格,由引理2.3 知,E不是反一致的, 矛盾. 从而,E是链.

另一方面, 若E是链, 假设E是无限的, 即E是无限链, 由E满足极大条件, 即E为满足极大条件的无限链, 又由引理2.2 知,E是一致半格, 这与E是反一致的矛盾,从而E是有限的, 即|E|<+∞.

由以上定理可知, 设E是满足极大条件的反一致半格, 则E只可能出现两种情况,一种是有限链, 另一种是非链的无限半格.

例2.4设E是半格,E的Hasse 图如图4:

图4

由图4 可知, 对于任意e,f ∈E,(e ̸=f), 有Ee≇Ef, 即

由定义1.4 可知,E是反一致半格, 显然,E满足极大条件, 从而E是满足极大条件的反一致半格. 由图4 可见,E是无下界的非链半格, 即E是非链无限半格.

上述例子表明, 满足极大条件的反一致半格是非链的无限半格. 易知, 任何有限链都是满足极大条件的反一致半格.