感应电机模型预测起动控制策略

刘 聪，韩亚丽

(中原工学院 信息商务学院，郑州 451191)

0 引 言

近年来，模型预测控制(Model Predictive Control，MPC)已广泛应用于电机驱动领域[1-2]。其中研究热点集中在参数鲁棒性分析，以及一些实际应用问题[3]。对于大功率电气传动系统，文献[4]提出了一种球形译码算法来解决MPC控制中的预测周期较长的问题。对于小功率驱动系统，主要是研究如何降低复杂性和扩展应用范围，如文献[5]提出的模型预测磁链控制和文献[6]提出的模型预测占空比优化算法等。

感应电机驱动通常使用无速度传感器方案，因为其有诸多优点，具体实现方法通常有模型参考算法[7]，卡尔曼滤波器算法[8]和自适应全阶观测器算法[9]等。无速度传感器控制通常和MPC控制结合使用，并在较宽转速范围内可实现较好的性能，但鲜有文献报道MPC控制起动问题，而实际中却存在电机起动问题[10]。由于感应电机驱动系统重起时的初始转速未知，若不能正确判断，则将产生较大浪涌电流，导致保护停机。而自适应全阶观测器(Adaptive Full Order Observer，AFO)算法由于引入了定子电流误差反馈，在较宽的转速范围内具有很好的转速估计精度和对系统参数较高的鲁棒性[11]，故考虑引入到重起控制设计中。综上，本文提出了一种感应电机模型预测起动控制策略，新方案实施简单，不仅适用于电机初速估计，而且适用于正常运行。最后，基于实验平台进行了实验验证。

1 感应电机数学模型

将定子磁链ψs和定子电流is选为状态变量时，感应电机的数学模型可表示为[12]

px=Ax+Bu

(1)

(2)

B=[λLr1]T

(3)

(4)

电磁转矩可表示为

(5)

式中，Np为极对数，⊗表示交叉乘积。

2 自适应全阶观测器

2.1 AFO的数学方程

基于式(1)，可以构造AFO如下[13]：

(6)

式中,us为定子电压，上标“^”代表估计值，G为AFO的反馈增益矩阵，具体为

(7)

式中,g1和g2为G的元素，而g1r和g1i为g1的实部和虚部，g2r和g2i为g2的实部和虚部。基于Lyapunov定理，估计转速自适应定律为

(8)

进一步推导为

(9)

(10)

2.2 基于AFO的电机重起过程分析

基于式(1)至式(6)，可以推导出误差动态方程为

(11)

(12)

(13)

a1=-λ(RsLr+RrLs)

(14)

(15)

m=λ(RsLr+RrLs)+g1r-j(ωr-g1i)

(16)

n=λRr(Rs+g2r)+λLrωrg2i-j·y

(17)

y=λLrωr(Rs+g2r)-λRrg2i

(18)

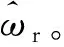
(19)

(20)

(21)

现在可定义Lyapunov函数V如下：

(22)

假设ωr在一个控制周期内不变，则V的导数为

(23)

pV<0

(24)

(25)

基于式(15)和式(19)，式(9)中的sinθ可计算如下：

(26)

因此，如果在整个重起过程中式(27)成立，则式(9)中的sinθ值将和ωr一起改变符号，故满足式(25)。

(27)

通过对上式进行求解，如果设置反馈增益矩阵G为零矩阵，则可获得以下不等式：

(28)

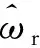
(29)

式中,ωmax为最大转速的绝对值，上式还意味着必须估计电机旋转方向。然而，如果在旋转方向上存在检测误差，估计转速将会收敛到零，这是因为一旦估计转速过零，式(25)就不会满足。为了避免转速方向信息的依赖性，可选择g2为

g2=-Rs

(30)

那么，式(19)可重写为

(31)

d=λ(RsLr+RrLs)+g1r

(32)

类似式(27)推导，应使下式成立以满足式(25)。

d>0

(33)

从式(32)可看出，不再需要选取合适的初值来确保收敛。通过求解式(33)可得到g1r为

g1r=hλ(RsLr+RrLs)

(34)

h>-1

(35)

考虑到g1i对本文研究无任何影响，将其设置为0。因此，提出的反馈增益矩阵可总结为

(36)

3 MPC控制

3.1 基本原理

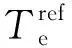
(37)

图1 MPC控制器框图

考虑到数字控制器实现MPC控制时需要对延迟进行补偿，这里采用了两步预测方案[14]。成本函数可以构造为如下形式：

(38)

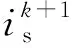
(39)

对于两电平变频器，有8个开关状态和7个不同的电压矢量，如图2所示。将每个可行电压矢量代入成本函数计算选择具有最小结果的矢量作为下一个控制周期的输出。

图2 两电平变频器输出电压矢量

在高速运行期间，定子电阻上的压降可忽略不计。若采用圆形磁通轨迹，则所需电压可近似为us=pψs=jωeψs。在实际应用中，轨迹应控制在图2中六边形内部，故定子磁链的最大值应满足下面的不等式。

(40)

式中,Udc为直流电压。考虑到式(40)的约束，可将磁链幅值ψref设置如下形式，以实现弱磁工况。

(41)

3.2 无速度传感器MPC控制下的重起策略

为了实现无速度传感器MPC控制，将第2节中设计的AFO引入到MPC控制器中，并使用估计转速代替测量转速用于预测计算。在对转速进行估计时，转矩参考设置为0，并且以前馈方式给出定子磁链的参考值为

(42)

(43)

初始转速估计值置为0，从而可快速响应两个不同的旋转方向。为了避免触发过流保护，需要在成本函数中增加电流幅值的限制，具体如下。

(44)

(45)

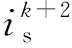
基于式(1)至式(4)推导，可得以下等式：

pψr=λLmRrψs-(λLsRr-jωr)ψr

(46)

(47)

从上式可看出，如果实际转速和估计转速之间存较大差异，则ψr的幅值将远小于ψs的幅值。若估计转速等于实际转速，则ψr的幅值为

|ψr|=Lm|ψs|/Ls

(48)

因此，|ψr|和Lm|ψr|/Lr之间的误差越小则表示估计转速逼近实际转速。在实际应用中，当下式成立时，起动过程完成且随后恢复到正常运行。

(49)

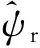
值得注意的是，在对转速进行估计后，反馈增益矩阵G可切换到正常运行下更为优化的类型，具体如下所示[2]：

(50)

其中,b为恒定的负增益。

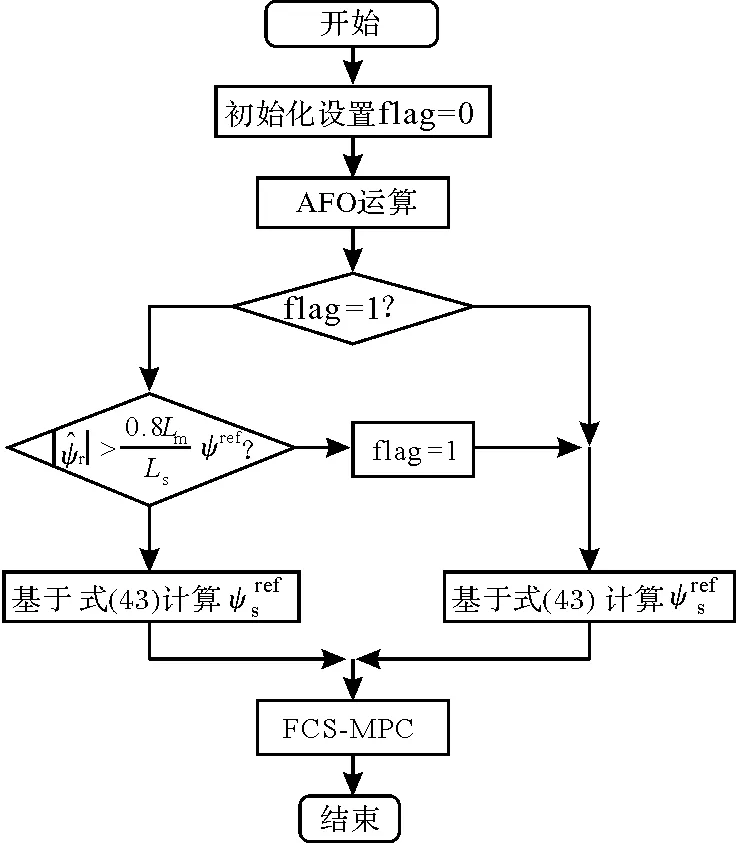
图3 无速度传感器MPC控制下的重起策略流程图

4 实验验证

为了验证新的基于MPC和AFO的感应电机重起策略，构建了如图4所示的测试平台。控制算法基于TI公司32位浮点DSP(TMS320F28335)上实现。控制器内部变量通过DSP的DA接口最终显示在示波器上，定子电流波形由电流LEM传感器测量得到，实际转速通过增量式编码器进行测量得到，只用于示波器显示比较，不参与控制。感应电机和测试系统的主要参数如表1所示。

图4 实验平台

表1 感应电机和实验系统参数

图5 电机重起实验波形

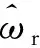
图6 电机带额定负载起动波形

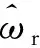
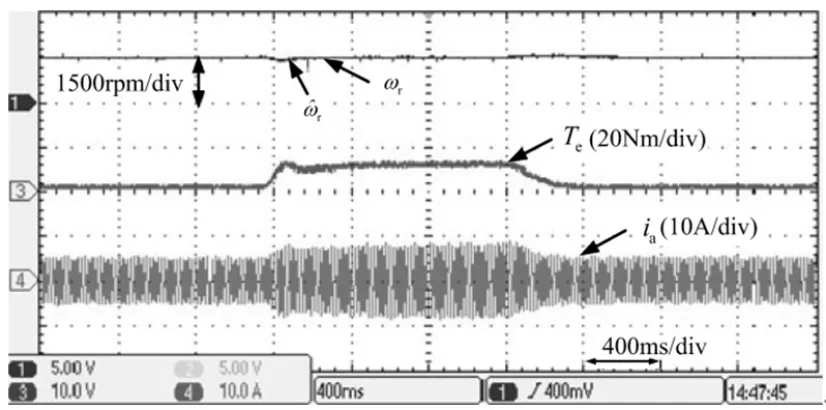
图7 突加负载测试波形

5 结 语

针对基于感应电机的电力传动系统在工程实践中出现的飞车起动问题，本文设计了一种基于AFO和MPC的无速度传感器重启控制策略。对设计和实验过程进行总结，可得到如下结论：(1)首先，分析了系统重启过程中AFO的收敛条件，然后推导出反馈增益矩阵，免去了对旋转方向的估计，同时保证了估计转速可收敛至任何初始转速；(2)在MPC控制的基础上，融入AFO，并考虑将输出电流限值融入到成本函数，保证了重启过程的安全、平稳和快速；(3)通过重启实验、带载起动实验和突加负载实验，验证了所设计控制器的有效性。