基于等宽极厚调制的永磁电机优化设计
2019-03-26朱一昕张高峰
朱一昕,张高峰,钱 新
(江南大学,无锡 214122)
0 引 言
随着高性能永磁材料的出现和市场对高精度电机的迫切需求,永磁同步电机以其高效率、高功率密度等优点在各行各业都得到了广泛的应用。高性能永磁电机对电机转矩脉动具有较高要求,永磁同步电机转矩脉动与电磁转矩脉动和齿槽转矩密切相关,电机气隙磁密的谐波含量将导致电机反电动势正弦度变差,产生电磁转矩。因此,提高永磁同步电机气隙磁密正弦度和削弱齿槽转矩对生产高性能电机具有十分重要的意义[1]。
对于表贴式永磁同步电机,永磁电机的气隙磁密接近矩形波,含有大量谐波。文献[2-3]分别采用Halbach阵列和不均匀气隙的方法来优化永磁同步电机气隙磁密,取得了较好的效果;文献[4]采用永磁体正弦充磁优化永磁电机气隙磁密,提高了气隙磁密正弦度。电机齿槽转矩是电机固有问题,会导致永磁电机转矩脉动。文献[5-7]采用永磁体斜槽方法来削弱齿槽转矩;文献[8-9]采用分组磁极和槽口偏移来优化永磁电机齿槽转矩;文献[10-11]提出采用永磁体等厚极宽调制来抑制电机齿槽转矩。
本文提出了采用等宽极厚正弦调制的方法来优化永磁同步电机气隙磁密和齿槽转矩,通过将整块永磁体分成多块极弧系数相等、厚度按正弦调制的分块磁体来抑制气隙磁密谐波和齿槽转矩,相比前人提出的永磁体等厚极宽正弦调制的方法,该方法使气隙磁密波形更加平滑,更有利于气隙磁密和齿槽转矩的优化;为了验证该优化方法的正确性,使用Ansoft有限元软件搭建电机模型进行了仿真分析,结果表明该方法能有效的改善永磁同步电机气隙磁密,并在一定极弧系数范围内能削弱电机齿槽转矩。
1 理论基础
1.1 等宽磁极厚度调制
由文献[12]可知,忽略饱和、漏磁,假设永磁体的磁导率与空气相同,气隙磁密可表示为
(1)
式中,B为剩磁,与永磁体材料相关,为常数;hm为永磁体厚度;δ为气隙长度;对表贴式永磁同步电机,忽略定子齿槽影响,hm+δ为转子外表面和定子内表面间距,定子和转子是同心圆,则hm+δ为常数。则
Bδ=khhm
(2)
式中,kh为磁密与永磁体高度比例系数,为常数。因此,当永磁同步电机磁极厚度正弦分布时,气隙磁密将接近正弦波,能够削弱永磁电机气隙磁密中的谐波含量。
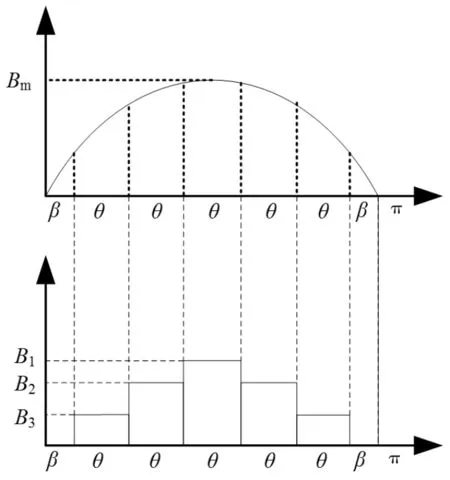
图1 分块磁极阵列图
根据文献[10-11],等宽磁极厚度正弦调制的原理为,一个磁极期望实现的正弦气隙磁场波形可表示为B=Bmsinθ将其分成N等分,将整个磁极看成由N个等宽不等厚的永磁磁势序列产生的气隙磁场合成波形。用N个等宽不等高的矩形磁场分量波形来代替期望的正弦气隙磁场波形,使矩形波的中点和相应正弦波分割部分的中点重合,当矩形波和相应正弦波分量部分的面积相等时,矩形波产生的磁场分量可近似表示为正弦波当前位置的磁场分量,假设永磁体分块数为5,则可表示为图1所示。
图中,Bm为气隙磁密基波分量幅值;N为永磁体分块数,不同极性的相邻永磁体间距为2β,βi表示第i块磁极产生的气隙磁密。
设普通电机永磁体厚度为h0,气隙磁密基波分量对应的永磁体厚度为hm,根据式(2)可得
(3)
式中,B0为矩形波气隙磁密幅值;根据矩形波与基波分量关系可得
(4)
各分块永磁体厚度与磁密的关系为
(5)
根据图1,式(4)和式(5),可得分块永磁体厚度在一个磁极下与空间电角度的关系如下
(6)
其中,i=1,2,…, 0≤Nθ≤π
(7)
式中,θ为每块磁极所占的电角度;N为永磁体分块数;hi为第i块永磁体的厚度;相邻永磁体间距为2β电角度;p为磁极对数;αp为极弧系数。
式(6)可进一步表示为
(8)
1.2 齿槽转矩
永磁同步电机齿槽转矩来源于永磁体与电枢齿之间的相互作用力,定义为磁场能W量与位置角α之间的偏导数之比,即:
(9)
在转子旋转过程中,永磁体能量基本不变,故电机的磁场能量可近似为
(10)
气隙磁密沿电枢表面的分布为
(11)
则
(12)
对于普通电机,一对磁极下的气隙磁密分布可表示为
(13)
式中,θ为机械角度,p为永磁同步电机极对数,αp为极弧系数;B2(θ)为偶函数,在一个周期内,B2(θ)可展开为
(14)
(h(θ)/(h(θ)+δ(θ,α)))2为偶函数,在一个周期内可展开为
(15)
式中,Ba和Ga为常数;Q为电机槽数,α为定转子相对位置;Bn和Gn为傅里叶系数。
将式(14)和式(15)带入式(12),再将式(12)代入式(9)可得
(16)
式中,kcog为齿槽转矩相关系数。
为简化计算,采用永磁体等宽极厚调制的气隙磁密可近似为
(17)
式中
分别对B2(θ)和B′2(θ)进行傅里叶展开
B2(θ)的傅里叶系数为
(19)
B′2(θ)的傅里叶系数为

(20)

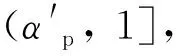
2 仿真验证
2.1 气隙磁密
采用Ansoft软件进行仿真验证,设计一台标准表贴式永磁同步伺服电机样机模型参数如表1所示。

表1 电机模型
设置电机极弧系数为1,采用等宽极厚正弦调制方法对普通永磁同步电机气隙磁密进行优化,由表1可得h0=2mm,根据式(4)可得hm=2.5mm;极弧系数为1,则β=0,以永磁体分块数为5块为例,由式(8)可得各块永磁体厚度为h1=0.32hm,h2=0.8hm,h3=0.98hm,h4=0.8hm,h5=0.32hm,搭建电机模型如图2所示。

图2 永磁体分块数为5的电机模型
同理,可得到永磁体分块数为3和7时的永磁同步电机参数。对普通电机和分块数为3、5、7的永磁同步电机进行仿真分析,得到结果如图3所示。
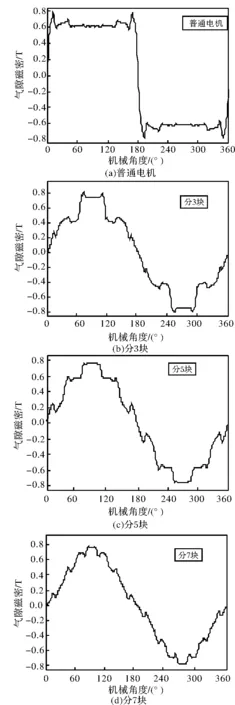
图3 电机气隙磁密
由图3可知,当极弧系数为1时,普通永磁同步电机的气隙磁密谐波含量很高,采用等宽极厚调制后,电机气隙磁密得到改善,普通电机的气隙磁密畸变率为40%,永磁体分3块进行正弦调制的气隙磁密畸变率为22%,分5块的气隙磁密畸变率为10%,分7块的气隙磁密畸变率为9.6%;对比文献[10]可知,采用该方法的气隙磁密比较平滑,可知,该方法能够很好的优化永磁同步电机气隙磁密,大大减小了电机气隙磁密谐波含量;同时也可以得到,随着分块数逐渐增加,气隙磁密优化效果逐渐减弱。
一般情况下,极弧系数不会为1,设置极弧系数为0.75,由式(7)可得,此时β=π/8,由式(8)可计算电机相关参数。使用Ansoft有限元分析软件进行仿真分析,得到气隙磁密谐波幅值如图4所示。从图中可知,普通电机的谐波畸变率为20%,分3块的气隙磁密畸变率为16%,分5块的气隙磁密波形畸变率为8%,分7块的气息磁密畸变率为9%,可知,当极弧系数为0.75时,该方法也能很好的优化永磁同步电机气隙磁密。同时也可以看到,采用磁极等宽极厚正弦调制时,基波幅值和普通电机基本一致,表示该方法不会导致气隙磁密基波分量的下降,因此不会导致平均电磁转矩降低。
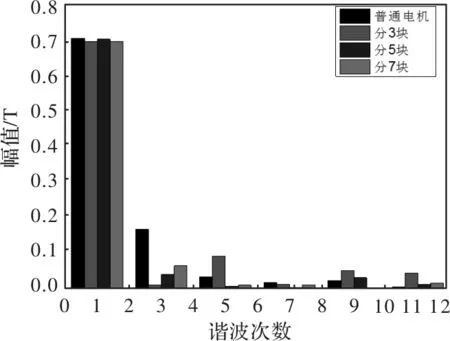
图4 极弧系数为0.75气隙磁密谐波幅值
2.2 齿槽转矩
分别搭建搭建24槽4极、18槽4极和18槽2极永磁同步电机仿真模型,由式(16)可知,24槽4极电机的n=6次磁密谐波对应齿槽转矩的基波分量,n较大,式(21)满足要求,同理可得18槽4极和18槽2极永磁同步电机同样满足要求。如图5是不同极槽下普通电机和等宽极厚调制电机齿槽转矩随极弧系数变化曲线


图5 永磁电机齿槽转矩随极弧系数变化曲线
如图6为24槽4极永磁同步电机不同分块数下的齿槽转矩随极弧系数变化曲线。

图6 不同分块齿槽转矩随极弧系数变化曲线
从图6可以看到,整体上,随着分块数的增加,齿槽转矩逐渐减小,分块数为7时,齿槽转矩最小。
2.3 转矩脉动
如图7所示为24槽4极永磁同步电机在极弧系数为0.75时,永磁同步电机带额定负载的输出转矩波形图。

图7 电机输出转矩波形
从图7可以看到,普通永磁同步电机输出平均转矩为7.64N,转矩脉动为5.3%;分5块的永磁同步电机输出平均转矩为7.8N,转矩脉动为3.5%;分7块的永磁同步电机平均输出转矩为7.5N,转矩脉动为1.8%。可知采用等宽极厚调制的电机输出转矩和普通电机没有太大差别,没有出现输出转矩变小的问题,同时转矩脉动比普通电机转矩脉动要小,证明了该方法能够削弱永磁同步电机转矩脉动。
综上所述,采用磁极极宽等厚正弦调制设计永磁同步电机时,选择分块数为7能够取得较好的效果,气隙磁密、齿槽转矩以及转矩脉动都得到了优化。
3 结 论
本文提出了采用分块磁极等宽极厚正弦调制方法来优化电机气隙磁密和齿槽转矩,通过对分块永磁体的厚度进行正弦调制,提高了永磁同步电机气隙磁密的正弦度,减小了气隙磁密的谐波含量;同时,在一定极弧系数范围内,该方法也能够削弱永磁同步电机齿槽转矩。使用Ansoft有限元分析软件设计永磁同步电机进行仿真验证,结果表明该方法能够较好的优化永磁同步电机气隙磁密和齿槽转矩,减小电机转矩脉动,并且不会导致电机平均输出转矩出现下降,并且分块数为7时各方面优化都取得较好的效果。相比采用永磁体等厚极宽调制的方法,该方法气隙磁密更加平滑,同时,相比其他优化方法,该方法不会导致电机电磁转矩的下降。
