双定子球形电机空间磁场的谐波分析

张冰娇，吴凤英，张宗楠

(天津理工大学 天津市复杂控制理论与应用重点实验室，天津 300384)

0 引 言

具有多自由度的球形电动机因其高机械集成度、有效材料利用率高引起人们广泛的关注。球形电动机按其原理可以分为:自整角机式、感应式、永磁式、多自由度电动机等[1]。随着稀土永磁材料的发展和在电机中的应用,具有多自由度的永磁式球形电动机的研制开发具有前沿性。目前永磁球形电动机研究较多的是步进、变磁阻和同步电机[2]。球形电机结构的差异性和复杂型使得在对磁场分布进行分析时需采用不同的方法，而解析法虽然可以得到较好的分析结果，但只适用于特殊构型的球形电机。

针对以上问题，为提高球形电机的转矩，设计一种新型双定子永磁球形电动机，具有特殊的内部开域外转子结构。该电机可以充分利用内部空间，内外部磁场耦合良好，由于谐波不产生转矩，对球形电机进行磁场建模和磁场分析是对后续运动控制研究的基础。并且对电机转子结构参数磁场气隙磁场分布分析是实现电机磁场分析必不可少的环节[3]。最后搭建的样机实验平台，实验表明基波分量实验值较理论值可以基本符合变化规律。

1 电机机械结构及其运行原理

新型双定子球形电机的定子是单层铝材料球体，壳体上分布三层集中绕组，每层八个电枢线圈，分布于赤道两侧的线圈结构尺寸相同。球形转子由支撑杆支撑，与定子绕组间形成内外两层气隙，其中稀土永磁体分为铁心外永磁体和铁心内永磁体，分别吸附在铁心内外且同一组铁心内外永磁体固定在同一水平线上。四对固定在铁心上的永磁体均匀排列在铁心四周且相邻两个永磁体磁极方向相反。通过对定子线圈通电进行控制，实现三自由度运动，球形电机的结构示意图如图1所示。

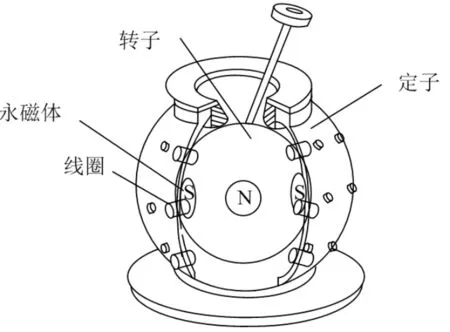
图1 电机结构示意图

电机的运行原理及其磁化方式如图2所示。电机可以在线圈不同的通电方式产生的足够大的电磁转矩作用下，实现不同形式的运动，分别为自转、俯仰、偏航3种方式的运动[4]。电机的永磁体排列方式，可以看成两台永磁电机的并联，内部的电机是开域的外转子形式且内外磁场独立。合理配置内外气隙使电机获得最大磁通密度，从而有效利用电机的内部空间。磁通密度分布围绕在永磁体周围，所以磁化方向从S极到N极，其中Ri是铁心的内半径，Ro是外半径。

图2 电机运行原理及磁化图

2 基于ANSYS气隙磁通密度谐波分析

2.1 建立三维有限元模型

有限元法是电磁场分析中电磁计算的主要方法，通常使用有限元法在较复杂的电机模型中。同解析法相比较，有限元法更简单、更快速且计算精度更高[5]，因此其常作为球形电机的电磁场计算方法。

由于双定子永磁球形电机结构的对称性，因此只选择一个定子和电机转子为研究对象，即分析单定子结构时的情况并对其进行建模。模型按照统一的国际单位制来定义材料属性、几何尺寸等输入数值，进行3-D磁场分析方法为棱边单元法，选用三维矢量位SOLID117单元，是六面体节点的单元，具有自由度：AX、AY、AZ。

通过Ansys APDL语言对转子铁心、永磁体、定子线圈、气隙进行参数几何建模。电机的主要结构参数如表1所示。

表1 电机结构主要参数

定子部分均采用硬铝材料制成，定子线圈为空心线圈，磁导率近似为空气磁导率。电机采用NdFeB(钕铁硼)永磁材料的矫顽力Hc为868kA/m，相对磁导率为 1.06。矫顽力分量MGXX、MGYY和MGZZ根据四对磁体在电机中的分布设定值。分别对体对象的线圈、永磁体和铁心，面对象的空气场分配属性如图3所示，用不同的颜色区分不同属性。

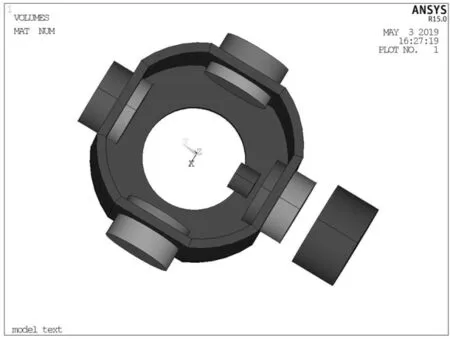
图3 电机的材料属性模型图

选择模型中所有的体单元，智能化网格划分参数并且设置尺寸等级为2，指定划分单元的形状为3D四面体单元。对选择的体单元进行网格划分，双定子永磁球形电机的三维定子网格划分有限元模型如图4所示。

图4 电机转子有限元模型

在施加边界条件时，要求磁力线平行于模型表面。根据电磁场边值理论，空气场的外表面约束表述为第一类边值问题，边界上无穷远处的磁力线平行[6]。在双定子球形电机有限元模型分析中，由于转子铁心是由硅钢片叠压而成，所以可以认为磁力线完全在模型内部，于是其边界条件如图5所示。边界条件的施加原则如表2所示。

图5 电机的空气场边界条件图

表2 边界条件的AZ值列表

模型中定子部分均采用硬铝材料制成，且定子线圈为空心线圈，磁导率近似为空气磁导率。给一对线圈施加环形电流密度5×106A/m2，线圈上的电流如图6所示。

图6 电机的线圈上的环形电流图

2.2 二维傅里叶变换

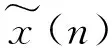
(1)

式中，r为任意整数。周期序列可用离散傅里叶级数来表示，周期为N的复指数序列的基频序列，表示为

(2)

式中，k次谐波序列表示为

(3)

对离散傅里叶级数，只能取k=0到N-1的N个独立谐波分量，因而式(1)可展开为如下

(4)

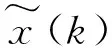
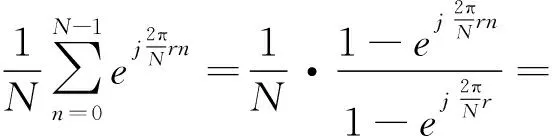
(5)

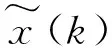
(6)

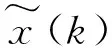
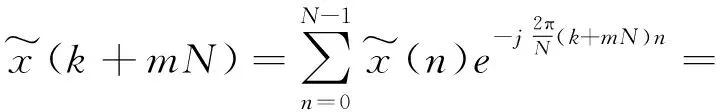
(7)

式(4)与式(6)为周期序列的离散傅里叶级数(DFS)对，并表示为

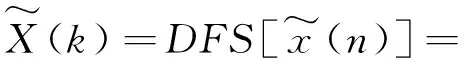
(8)

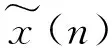
(9)

(10)

如果有

(11)

则有

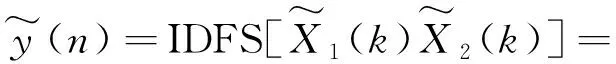
(12)

(13)

将式(13)带入式(12)则

(14)

将变量换元等价表示为

(15)

周期序列实际上只有有限个序列值有意义，因而其离散傅里叶级数表示式也适用于有限长序列，即为有限长序列的离散傅里叶变换。把长度为N的有限长序列x(n)看成周期为N的周期序列的一个周期，利用离散傅里叶级数计算周期序列的一个周期也就是计算了有限长序列。

快速傅里叶变换是离散傅里叶变换(DFT)的一种快速算法，由于球形电机球面上的数值分布，需要对获取的数据进行二维傅里叶变换。选用Matlab对双定子永磁球形电机有限元分析的径向磁通密度分量值进行二维傅里叶变换，其算法处理流程图如图7所示。根据离散傅里叶级数的复数形式和DFS的周期卷积和性质，径向分量值进行二维傅里叶分析后将得到各个频率上的数值即电机的基波分量。并且，分析傅里叶变换后的数值将符合原始数据的变换规则。

图7 电机气隙磁密谐波处理流程图

(1)获取气隙磁密数据

Ansys支持数据的导出，获取气隙磁通密度径向分量的数值，选定60mm处电机球面上的数值。设置径、纬度方向每间隔10°计算径向磁密，将614个数据写入.txt文件。

(2)数据分析

在Matlab分析之前，Ansys提取的球面数据将要展开为矩阵形式，即对获取的数据进行分析，删除位置重叠处的数值。

(3)移动频谱中心

永磁体磁极均匀分布在球面上，气隙磁密的数值在球面上的分布和磁极的分布一致。但为了分析电机基波分量的分布规律，需要对频谱图移动频谱的中心。

2.3 二维傅里叶谐波分析

由于气隙磁通径向基波分量在产生电磁转矩时为主要磁场，对气隙磁通密度的基波进行分析。永磁球形电动机气隙磁场沿φ和θ方向具有不同的谐波含量，反映了磁场的大小，又反映了磁场的分布形式[8]。通过Matlab处理有限元分析的数据，得到磁通密度径向分量的三维谐波分量。图8为气隙磁通密度基波径向分量随φ和θ的变化的空间分布图。

由图中可以看出，球形电动机气隙磁通密度谐波分量B1r沿φ方向主要含有 2、4、6、8、10 次谐波，θ方向含有1、2、3、4、5次谐波。同时可以看出，双定子永磁球形电机具有较大的气隙磁通密度基波幅值。根据傅里叶级数的复数形式和DFS的周期卷积性质[9]，数值符合周期性，波形符合卷积性。故而，理论上基波分量的数值是正确的，基波磁场的幅值比磁场磁通密度的幅值约高出10%。

图8 气隙径向磁密谐波分量

2.4 电机转子结构参数谐波分析

为了改善气隙的分布，选择径向气隙流密度中的高次谐波含量作为目标[10]，进行参数的敏感性分析。对于双定子永磁体转子，表3列出了永磁体阵列的分析变量和参数取值。

表3 转子结构参数取值范围

改变程序中转子结构参数的取值，分别进行有限元分析，将得到的数值矩阵导入Matlab中进行二维傅里叶变换。参数变化与谐波幅值、体积的曲线图如图9～图11所示。

如图9(a)所示，随着永磁体厚度的增加气隙磁通密度基波幅度减少。永磁体越厚，产生的磁场越大，但在Di=4mm左右增幅开始发生变化，厚度的增加对磁场的影响越来越小。

从图9(b)中可以看出外部永磁体，气隙磁通密度基波谐波幅度与磁体的相对体积变化相近。外部的磁体的体积变化对磁场有较明显的影响，但这种增幅在Do=11mm左右开始发生变化。

图9 永磁体厚度基波幅度随体积的变化

图10 永磁体半径基波幅度随体积的变化

从图10(b)中可以看出外部永磁体，气隙磁通密度基波谐波幅度与磁体的相对体积变化相近，成正比例增长。说明外部的磁体的体积变化对磁场有较明显的影响，但在实际制作中需要考虑电机机械结构要求的限制。

图11 铁心厚底基波幅度随体积的变化

3 实验验证

根据双定子球形电机的试验台的设计，在有限的工艺和条件下，将试验台的基本结构加工出来。搭建电机样机实验平台，对实际磁场的分布进行测量，对比仿真的气隙磁场磁通密度。图12为转子磁场分布的测量系统。3个增量式光电编码器用来测量球形电动机3个正交轴方向的角度，以确定球形转子方位，使用高斯计测量电机空间位置的磁通密度。

图12 电机磁场分布的测量系统

利用高斯计对磁场进行测量，高斯计是根据霍尔效应原理制成的测量磁感应强度的仪器，它由霍尔探头和测量仪表构成。霍尔探头在磁场中因霍尔效应而产生霍尔电压，测出霍尔电压后根据霍尔电压公式与已知的霍尔系数就可以确定磁感应强度的大小。采用 HT108毫特斯拉计，表4为HT108 毫特斯拉计的技术参数。

表4 HT108 毫特斯拉计的技术参数

获得电机在各个位置角度的各个气隙磁通密度径向分量值所采取的实验方法是固定电机各个参数和电机定子的位置，在转子处于不同电角度情况下进行一系列的仿真计算并得到一系列的结果，再使用高斯计测量相同电角度下的测量结果，得到实验和仿真结果的对比。

图13 B1r分析结果与实验结果磁场分布对比图

为了验证本文所采用的双定子永磁球形电机气隙磁场有限元计算的准确性，将本文的仿真结果与实验结果进行了对比。基于有限元方法对电机性能进行仿真，并改变电机转子在电机中的电角度，进行一系列的仿真计算，相比较高斯计测得的试验数据。对电机不同位置下，沿纬度角θ方向和经度角φ方向的气隙磁通密度进行了对比，图13为r= 60mm和φ= 0°,φ=90°,θ= 90°方向仿真结果与实验结果所得变化曲线对比图。

可以看出，该分析方法得到的磁场结果与实验结果分布基本一致，由于电机磁场的漏磁和实际电机模型产生的偏差，实验的幅值大小与仿真得到的结果存在一定的误差但保持在20%～30%，实验允许存在。

然而考虑实际情况，制作的球形电机结构的各个参数之间由于高度的非线性会影响电机的性能。同时考虑到电机成本、绕线工艺等问题，电机结构参数的精确度比较难做到，在参数化有限元谐波分析的研究基础上，仿真的原始样本数据需要进行进一步的分析研究。

4 结 论

提出了一种新型双定子永磁球形电动机，分析了电机径向气隙磁通密度的分析谐波模型，以及转子结构参数对基波谐振幅度的影响。永磁体的厚度，半径和转子铁心的径向磁通密度谐波分析表明，对于给定的体积，存在最小的谐波振幅。搭建电机的样机实验平台，实验进一步验证了有限元模型的适用性以及转子结构参数对电磁场作用的影响。