微观企业全要素生产率的度量

王 健，胡美玲

（1.济南大学 商学院，济南 250002；2.山东管理学院 经贸学院，济南 250357）

0 引言

新常态经济的一个显著特征就是增长动力的转换，即从“规模速度粗放增长”向“质量效率集约增长”的转换过程。根据Solow（1956）提出的核算框架，经济增长的决定因素主要依靠要素投入量的增加和全要素生产率（total factor productivity，TFP）的提升[1]。但要素投入量的增加是一种粗放的要素驱动型增长，是不可持续的，因此TFP的增长成为新常态下经济增长的源泉。但是过去关于TFP的研究多基于宏观层面，而忽略了微观企业的异质性，导致不能正确衡量各个企业间的要素报酬，无法评估特定政策环境下企业的技术选择倾向，达不到资源的优化配置[2]。近年来学者们开始关注FDI、研发资本、创新对TFP的提升效应，企业间、产业间配置效率的差异性，制度环境、政府管制对TFP的影响等，这一切研究的前提都是合理度量企业的TFP。

学者们通过不同方法度量微观企业的TFP。覃家琦等（2009）[3]采用随机边界生产函数度量微观企业的投资效率。刘小玄和吴延兵（2009）[4]采用生产率理论中的DEA-M指数法度量企业生产率增长及来源。聂辉华等（2014）[5]运用OP法来估计企业TFP。赵奇伟（2016）[6]采用LP法度量TFP，研究企业生产率的动态演化。杨汝岱（2015）[7]通过运用OP、LP法研究我国制造业企业TFP的动态化，分析我国经济结构转型问题。李唐等（2016）[8]分别采用时间序列DEA、随机前沿SFA和LP模型进行度量，并运用主成分分析对这三种模型得到的企业TFP进行线性加总，得到新常态下企业的TFP。张志强（2015）[9]指出OP、LP、ACF法高估了企业的TFP，De Loecker、GRN和联合估计的TFP度量方法能够得到TFP的稳健估计。因此，准确合理地度量企业TFP成为迫切需要解决的问题。本文首先分析OLS法度量企业TFP时存在的偏误及其对模型估计的影响，然后对度量生产函数的常见方法进行梳理和比较，为度量微观企业TFP选择合适的度量方法。

1 企业全要素生产率的OLS度量

经典的企业TFP度量是用最小二乘法（ordinary least square，OLS）测算索罗余值（Solow Residual，指企业实际观察值和由OLS计算所得的估计值之间的差额）来实现的。下面介绍OLS法度量企业TFP的基本原理。

假定企业的生产函数为柯布-道格拉斯形式：

式（1）中，Yit、Mit、Kit和Lit分别是企业i在t年的产出、中间投入、资本和劳动，Ait是Hicks中性效率（Hicksian neutral efficiency），βl、βk和βm分别表示劳动、资本和中间投入的产出收入弹性。将式（1）对数化，得到其线性形式：

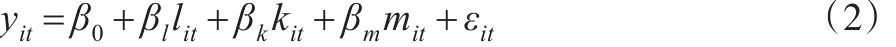
其中，log(Ait)=β0+εit；β0指全部样本企业的平均效率；εit表示误差项，指企业i的生产效率与样本企业平均效率的偏离水平，可以进一步分解为两部分，即εit=ωit+μit。其中，uit为随机扰动项，代表模型的度量误差或者企业不可观测的技术冲击，且uit与投入要素不相关；ωit为企业i在t时刻的生产率水平，是企业可观测但研究者不可观测的部分，指企业的技术管理水平或者是企业已预料到的冲击[10]。式（2）可以表示为：

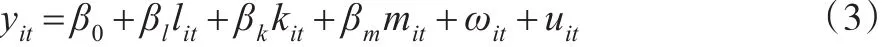
通过式（3）可知，ωit的估计值ω̂it为：

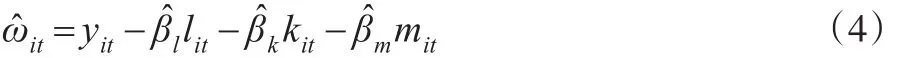
因此，企业i在t年的生产率可计算为

2 OLS度量企业TFP时存在的问题

2.1 联立性偏误

Andrews（1945）指出企业对自身生产过程较为熟悉，能够察觉部分生产率的变动，及时调整要素投入数量，使其利润最大化。企业生产过程中的投入要素与生产率变动的相关性，使得企业的生产率（被观测部分）的变动影响到投入要素的选择[11]。Loecker（2011）把联立性偏误定义为企业的要素投入决策与生产率的冲击（productivity shocks）相关而导致的估计偏差[12]。在这种情况下，高生产率冲击将导致企业增加要素投入，即E(xitωit)＞0，其中，xit=(lit，mit)①本文全部假定劳动力和中间投入为自由变量，企业在短期内根据对生产率的判断来调整劳动力和原材料的投入，他们与生产率的相关性更高。。当用OLS回归式（3）时，造成劳动力、中间投入被高估，资本系数被低估[13]②当存在多种投入要素的内生性问题时，OLS估计量的资本要素系数偏差未知。。

2.2 选择性偏误

在选择样本企业时，会碰到某些样本值缺失的情况，如果该样本值的缺失是由于生产率低、经营不善等原因退出市场的，则该缺失值是非随机因素。Henckman（1974）指出样本企业的非随机选择，将会导致度量企业TFP时出现选择性偏误。一些学者通过使用平衡样本来解决选择性偏误，但是平衡样本中的企业都是在观察期间内生产率维持较高而没有被淘汰的成功企业，不包括那些生产率水平较低、破产而被动退出市场的失败企业[8，14]。鲁晓东和连玉君（2012）[15]指出相对于资本存量小的企业，规模大、资本存量高的企业应对危机能力更高，在面对低生产率冲击时退出市场的概率较小，表明企业资本kit与企业退出市场概率负相关，导致资本系数βk被低估，继而引起企业的TFP被高估。

2.3 遗漏价格偏误

度量企业TFP时，由于各个企业的产品价格数据很难获得，通常使用工业产品出厂价格指数平减后的销售额来替代企业实际产出。Melitz（2001）[16]和指出只有在完全竞争产品市场、产品同质、无限需求价格弹性（infinite price elasticity of demand）时，才可使用行业价格指数作为企业产品价格的代理变量。Klette和Griliches（1996）[17]指出企业产品价格与要素投入相关时，投入要素的估计量有偏，造成度量企业生产率时存在遗漏产品价格偏误。把平减后的销售额代入式（3），得到对数化模型：

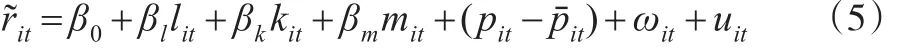
这里表示平减后的销售额，pit是企业产品价格，指行业产品价格。当企业产品价格高于行业产品价格时，使用行业产品价格进行平减，使得平减后的企业产量被高估，导致企业的TFP被高估。当要素投入量与公司产品价格相关时，，其中，xit=(lit，mit)。基于供求理论可知：企业要素投入量与企业产品数量正相关，企业产品数量与企业产品价格负相关，得到投入要素量与企业产品价格负相关，即，造成劳动力、中间投入被低估，资本被高估。

同理，鉴于企业各个投入要素价格的不可得性，企业的资本存量一般使用固定资产投资价格指数进行平减，中间投入使用原材料、燃料和动力购进价格指数进行平减，劳动人数表示的劳动力投入则不需要进行平减。如果投入要素市场处于不完全竞争条件下，将产生遗漏投入要素价格偏误。当投入要素价格高于行业要素价格时，使用行业要素价格进行平减，使得平减后的要素投入量被高估，导致企业的TFP被低估。把行业价格指数平减后的投入要素代入模型，得到：

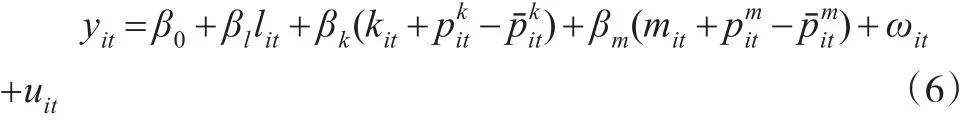
2.4 多产品问题

柯布-道格拉斯生产函数是建立在企业的生产技术水平不变，且只能生产单一产品的基础上的。当企业生产多种产品，并且多种产品具有不同的生产技术和产品需求时，企业会根据利润最大化原则，调整不同产品的产出，导致产生产品结构内生性问题。多产品问题仅存在于多产出公司（multi-product firms），当多产品企业的产出结构，投入产出水平和价格数据可得时，可以得到企业TFP的一致估计量。Bernard等（2007）[18]指出当数据不能获得时，通过考虑产出种类和每类产出的需求；或把企业分成若干组，每组企业生产单一产品的方式解决多产品的产出结构内生性问题。Loecker和Warzynski（2012）基于多产品厂商的行为框架，研究多产品企业的TFP。与多产品企业相比，单产品企业不能根据市场情况及时调整产品产出，导致其投入要素系数被低估。

综上所述，通过OLS度量微观企业TFP是有偏的。

3 解决方法

通过分析可知，运用OLS估算索罗余值的方法，度量微观企业TFP是不精确和有偏的，存在联立性偏误、样本选择偏误、遗漏价格偏误及多产品内生性问题。最新的研究关注于应用控制函数法（Control Function）度量企业的TFP，如OP模型、LP模型、ACF模型等，在这些模型框架下，Loecker（2011）[12]、Beveren（2012）[13]进一步提出相应的拓展模型。接下来针对OLS度量企业TFP时存在问题，梳理相应的解决方法并进行比较。

3.1OP模型

Olley和Pakes（1996）[19]最早运用半参数估计法（semi-parametric estimator）度量微观企业生产率，该方法使用投资作为生产率冲击的代理变量来解决联立性偏误，使用生存概率（survival probability）解决样本选择偏误。

假定劳动力和中间投入是自由变量（freely variable）①自由变量也称为可变要素，能够随时调整，对将来投资无影响且不进入投资函数。；资本是状态变量（state variable），当期资本取决于上期资本和上期投资，与当期投资无关，即假定投资是生产率的严格单调递增函数，在投资为正的情况下，投资函数对生产率的反函数为ωit=ω(iit，kit)。用投资函数的反函数作为代理函数，式（3）转换为：

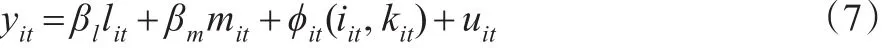
第二步：考虑样本的退出问题。根据Olley和Pakes（1996）[19]给出的Bellman方程，把企业生存状态记为dit，当企业持续经营时，dit=1；企业退出市场时，dit=0。企投资量和资本存量对数值的多项式。为说明半参数估计法对生产率的测算，将具体的估计过程分为三步。

第一步：依据式（8）进行回归，得到劳动、中间投入的一致估计量业是否退出市场取决于技术临界值当企业的生产率否则dit=1。通过Probit模型得到企业的生存概率P，即：

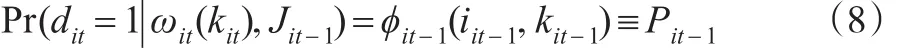
第三步：估计资本系数。生产率服从一阶马尔可夫过程，ξit是ωit期望的冲击，与投入要素不相关，是企业不可观测部分。将yit-βllit-βmmit的条件期望写成β0+βkkit加上生产率的条件期望，并整理得到：

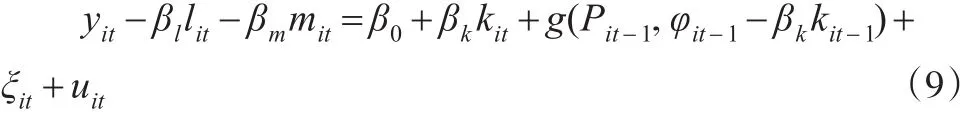
将在第一步和第二步估计中得到的β̂l、β̂m、φ̂it和代入式（9）得：

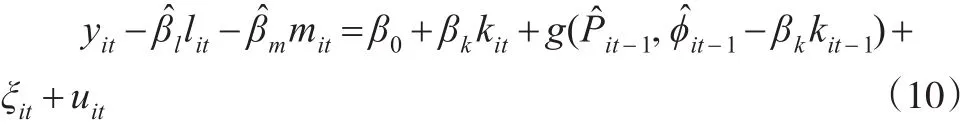
式（10）非线性模型有两种估计方法，第一种是通过搜索不同的βk取值，使得残差平方和最小的值就是③为 βk的任一可能的备选值，则可以预测 ωit每一期的值。即：使用这些预测值，通过可以得到的非参数一致估计那么关于的残差为因为kit取决于iit-1，那么当期的kit与当期的μit不相关，因此 βk的一致有效性估计可以通过得到。；第二种是再次利用四次多项式将近似展开。

3.2 LP模型

Levinsohn和Petrin（2003）[20]指出，OP模型中利用投资作为代理变量存在以下问题:一方面企业存在调整成本，使得部分企业的投资额为零。假定投资与总产出存在单调递增关系，表明投资额为零的数据无法估计，使得大量样本数据不能使用；另一方面存在非凸性调整成本，这使得误差项与投资之间存在相关性，导致投资不能完全响应生产率的冲击。Levinsohn和Petrin（2003）[20]使用中间投入作为代理变量，认为与投资作为代理变量相比，中间投入作为代理变量时，样本量损失较少，能够较好地解决生产函数的内生性问题，获得投入要素的一致性有效估计。LP法与OP法相比，在估计的第一阶段仅得到劳动的一致估计量，由于中间投入为代理变量，因此中间投入的估计是在第二阶段得到的。其次，在处理样本选择时，OP在第二阶段考虑了公司的生存概率，而LP没有考虑样本退出问题[21]。

3.3ACF模型

ACF模型认为OP和LP的生产函数估计在第一阶段将遇到共线性问题。OP、LP方法假定，劳动力lit是自由变量，能够随时调整，因此劳动并不是状态变量，并不影响生产率，没有进入投资函数。ACF认为，企业劳动调整成本很高（即劳动力并不是自由要素），劳动作为自由变量的假设过于严格。ACF假设lit是资本和生产率的函数：lit=f(ωit，kit)。在这种情况下，劳动力需求为：lit=f(ωit可知lit为资本和代理变量的函数，因而劳动力的系数βl在第一阶段不能通过四阶多项式估计得出。ACF模型是对OP模型的拓展，该模型假定所有的投入要素都是状态变量，生产率和投入要素影响到企业的投资决策，企业的投资函数为估计过程与OP法相似，但是第一步只能得到而劳动、资本、中间投入系数最后同时估计，通过非参数估计法得到要素投入的系数。

3.4 De Loecker模型

Klette 和 Griliches（1996）、Levinsohn 和Melitz（2002）提出使用有条件的需求系统（conditional demand system）解决不完全竞争市场中产品价格遗漏偏误[17，22]，基于此，Loecker（2011）[12]对OP模型进行拓展，假设企业生产单一产品面临的需求函数为：

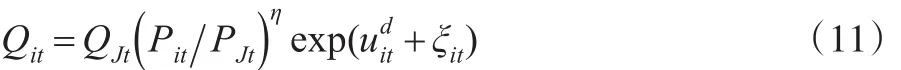
这里：Qit指企业i在t时的产品需求；QJt指行业J在t时的产品；Pit指企业i的价格；PJt指行业J的价格；指企业面临的需求冲击；η指行业内不同产品需求的替代弹性；ξit指不可观测的需求冲击（demand shocks），ξit与产出价格相关。将式（11）对数化，得：

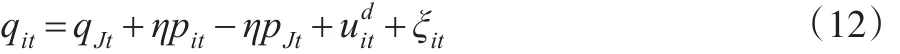
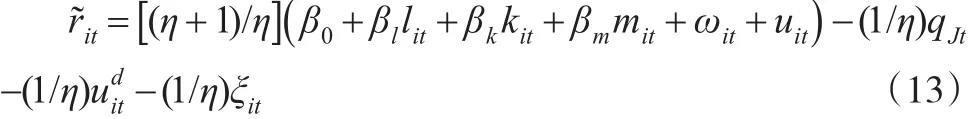
这里ωit的代理变量是投资①由于模型是对不完全竞争产品市场中OP模型的拓展，因此代理变量是投资；如果是对LP模型的拓展，代理变量则是中间投入。。从式（13）可知，通过添加( 1/ η )qJt到生产函数中代理不可观测的企业产品价格，把式（13）转化为最终测算公式，得到不完全竞争产品市场中投入要素的一致估计量：

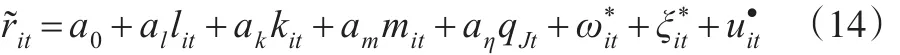
3.5 Beveren模型

不完全竞争产品市场下De Loecker模型涉及的是单一产品面临的需求函数，当涉及多产品企业时，需要考虑产品种类和每种产品的需求来解决多产品的产出结构内生性问题。假定行业内（industry）有N个企业生产M中产品，把行业细分为S个次级部门（sub-sector），当次级部门有不同的需求价格弹性时，生产函数为：

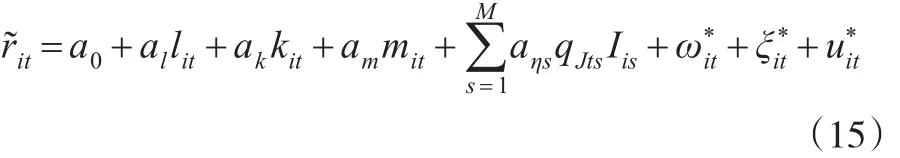
其中：s代表次级部门，M表示次级部门总量；Iis表示虚拟变量，如果公司i有次级部门s，Iis=1，否则为0；qJts指行业内不同次级部门的需求变动（demand shifter），用不同次级部门的产出表示；ηs指次级部门产品需求的替代弹性表示行业产出。从式（15）中可知，如果不同次级部门的需求价格弹性ηs不同，那么不同次级部门的投入要素系数βh和生产率ωit也不同，每个次级部门的βh、ωit等于式（15）测算出的的乘积。

综上所述，OP、LP、ACF、De Loecker、Beveren模型都是假定代理变量是生产率ωit的严格单调函数，ωit是唯一不可观测的状态变量，通过使用代理变量替代不可观测的生产率，解决联立性偏误（见下页表1）。在选择样本时，OP模型在评估第二阶段时解决了企业生存概率问题。De Loecker、Beveren模型是OP的扩展模型，通过把OP模型中的竞争性市场、公司生产单一产品的前提假设进一步放松，可以解决不完全竞争市场下的遗漏价格偏误和多产品公司的内生性问题。

4 结论

本文首先分析了使用OLS度量企业TFP时，产生的各种偏误及对估计结果的影响，然后对度量企业生产率的方法进行梳理和比较，得出的结论主要有以下几点：

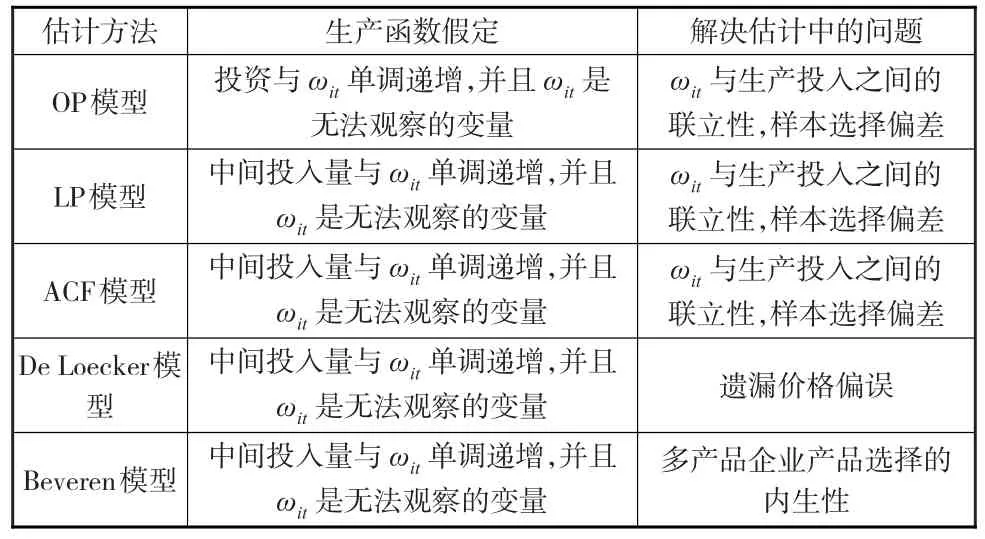
表1 企业TFP度量的解决方法

（1）通过OLS估算索罗余值来度量企业TFP时，首先分析了投入要素与企业生产率相关引起的联立性偏误和企业退出因素与生产率相关引起的样本选择偏误，得知这两种偏误都导致资本系数被低估。然后分析了不完全竞争市场中，企业价格与行业价格的差异引起的遗漏价格偏误，当企业产品价格高于行业产品价格时，导致企业TFP被高估；当企业投入价格高于行业投入价格时，导致企业TFP被低估。最后分析多产品企业存在产出结构内生性问题，导致投入要素系数被低估。因此，直接使用OLS度量企业层面TFP时，将导致估计结果非偏不一致。

（2）OP模型不但可以很好地处理联立性偏误，而且还能处理样本选择偏误。而LP与OP模型相比，较好地解决了数据丢失的问题，但是没有考虑样本退出问题，因此以中间投入品作为工具变量的LP模型并不显著地优于以投资额作为代理变量的OP模型。ACF模型放松了OP模型中的部分假设，认为企业投资决策不仅是资本的函数，还是劳动（或者其他投入要素）的函数，ACF模型的设定比OP模型更具一般性。De Loecker模型和Beveren模型主要针对不完全竞争市场和多产品企业的TFP度量。因此，在衡量企业TFP时，应该针对估计时存在的具体问题，选择合适的估计方法。

（3）就理论基础和度量方法而言，OP模型具有较高的价值，为解决生产函数估计中的联立性和选择性偏误提供了新的途径。寻找合适的代理变量以及构建可靠的企业行为模型，是这一方法的核心。由于OP模型中的生产函数假定完全竞争市场、规模报酬不变以及生产单一产品等，对于解决不完全竞争下价格遗漏偏误以及多产品公司的内生性问题，可以通过放松OP模型的部分假设，拓展OP模型得到企业全要素生产率的估计，这是生产函数估计方法的进步，也是今后的发展趋势。