不平等指数相对性指标的几何图解与实例对比

綦 路，陈 蔚

（山东大学 经济学院，济南 250100）

0 引言

不平等指数是指高收入和低收入的比例和，一般用不平等指数值表示社会不平等程度，反映社会贫富两极人口的分布特征[1]。不平等指数值越低则表示社会中等收入较多，社会分化程度良好，反之，不平等指数值越高则表示社会贫富分化严重[2]。计算不平等指数时，比较难界定高收入和低收入，因此产生了诸多不平等指数计算方法，一般分为两大类别，一类为绝对性指标，如方差、kolm指数和极差等，依据量纲对不平等程度进行绝对性计算。此类方法虽然计算流程简单，但在计算单位变化后，即使不平等程度未变化，计算结果也会变化，无法准确反映不平等程度[3]。另一类为相对性指标，比较常用的有基尼系数、泰尔指数、相对平均离差等，一般认为相对性指标优于绝对性指标，原因在于相对性指标避免了单位对指数的影响。但相对性指标计算方法众多，是否在面对所有问题时，可任意选取相对性指标计算方法。从学术研究成果看，目前没有任何一种相对性指标方法全面优于其他指标，每个不平等指标方法都存在局限性，如基尼系数无法体现不平等分布状态[4]、泰尔指数无法反映收入位置变动情况[5]。因此，在研究不同状态的不平等问题时，需根据不平等问题特征来选取合适的指标方法，特别是运用相对指标计算方法时，此类计算方法过程复杂、涉及变量多，如何选择计算指标方法成为重点。接下来对不平等指数计算中两类（基尼系数和泰尔指数）重要相对性指标方法进行研究，以确定这些相对性指标方法最适应哪种情形下的不平等指数计算。

1 基尼系数框架及其计算方法

1.1 基尼系数的基本理论框架

基尼系数是国际衡量不平等程度的通用指数，赫希曼发明后由基尼发扬壮大。赫希曼从洛伦茨曲线分布中发现不平等程度的面积比关系[6]，设实际收入曲线（洛伦茨曲线）与绝对收入平等线之间的合围面积为X，实际收入曲线（洛伦茨曲线）其他下围面积为Y，则基尼系数G可表示为：

从公式（1）可知，如果X值为0则基尼系数G值为0，表示社会处于完全公平状态；如果Y值为0则基尼系数G值为1，表示社会处于绝对不平等状态。如果以实际收入曲线（洛伦茨曲线）为参照线，实际收入曲线（洛伦茨曲线）孤度越大，基尼系数G值越大，不平等程度越大，反之，实际收入曲线（洛伦茨曲线）孤度越小，基尼系数G值越小，不平等程度越小。为更清楚地反映上述关系，利用几何图解方式将基尼系数表示为图1。

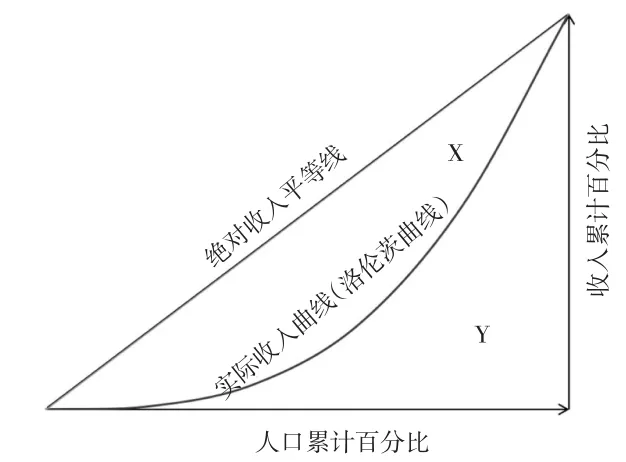
图1 基尼系数的几何图解关系

由几何图解和面积比公式可得基尼系数的取值范围为0～1，联合国开发计划署等组织根据不平等程度将基尼系数划分为5个等级，见表1。国际上将基尼系数0.382设为不平等程度的黄金分割律[7]，超过该数值则表示国家的不平等程度越高，一般发达国家的基尼系数区在0.2～0.38，我国2016年的基尼系数为0.465，远高于国际黄金分割律，不过随着我国经济的快速发展，预测未来5年内基尼系数有望降至黄金分割律之下。

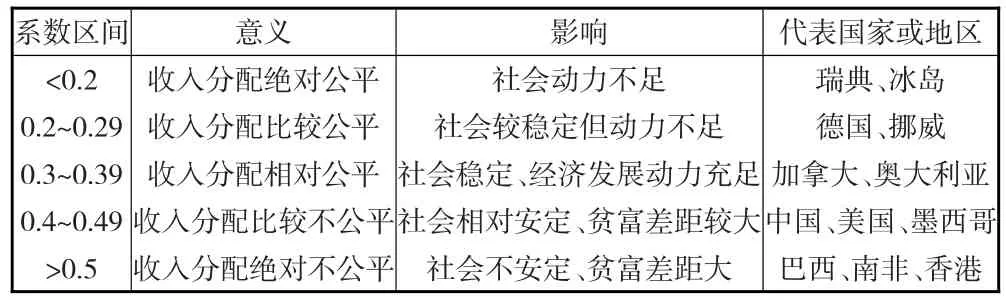
表1 基尼系数的国际等级划分及代表

1.2 基尼系数的计算方法对比

求解基尼系数的关键为计算面积比，而面积比的求解方式众多，因此学者对基尼系数的具体计算方法作了大量探索，椐不完全统计大约在15种左右，如直接法、平均差法、矩阵法、曲线拟合法等，接下来本文对应用比较广泛的积分法和几何分组法进行具体的对比。

第一，积分法。积分法的思路较为简单，由基尼系数的几何图解关系可知，绝对收入平等线下围是一个直角等边三角形，且二条直角边的长度为单位1（100%），按上述思路二条直角边分别定义为OA和OB，见图2。

即得到三角形AOB，那么就有：

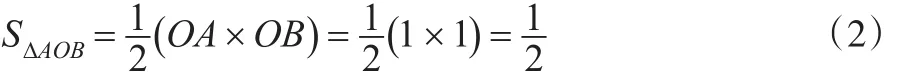
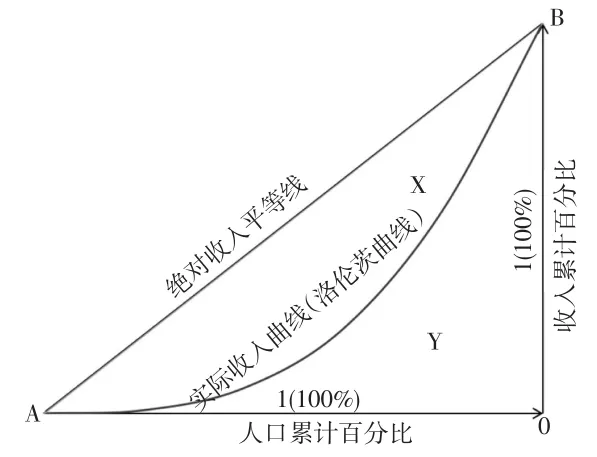
图2 基尼系数积分法的几何图解

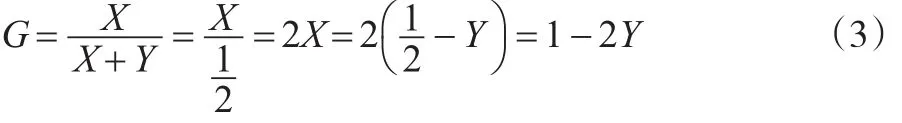
由公式（3）可知，积分法求解基尼系数的关键是图2中Y的面积。为得到Y面积假定实际收入曲线（洛伦茨曲线）满足函数f(x),则Y面积可以用函数f(x)在区间[0,1]的定积分表示。

将式（4）代入式（3），则可得到基尼系数G的最终公式为：

由此可见，积分法的关键是确定函数f(x)的形式，显然函数f(x)与人口累计百分比、收入累计百分比相关，利用回归分析法假定人口累计百分比为x，收入累计百分比为y，则有y=f(x)。在具体的基尼系数计算过程中，人口累计百分比x和收入累计百分比y为成对数据，只要对成对的x、y值进行回归拟合，则可得出函数f(x)的具体形式。

第二，几何分组法。积分法的优点在于能够比较准确地反映基尼系数，劣势在于要求用回归方法求得实际收入曲线（洛伦茨曲线）函数，对于符合函数规律数据而言，积分法无疑是最优求解方式，如果数据为非规律性函数则会产生误差。几何分组法避免了此类问题，在OA轴上取n个点，将面积Y划分为n份，见图3。

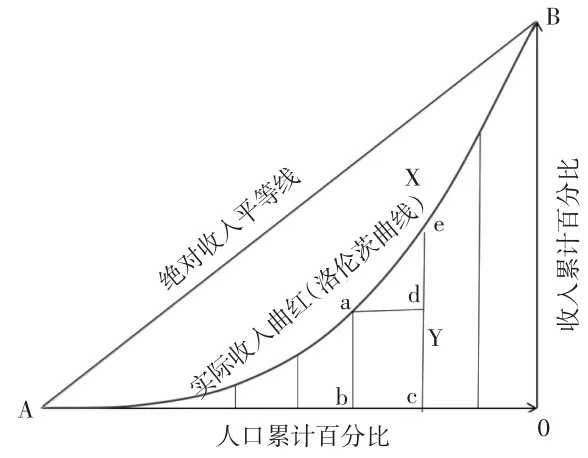
图3 基尼系数几何分组法的几分图解

每部分以直代曲的方法求解面积，最后加成n份的总面积。由于直代曲存在误差，只有将n取值为无穷大时，误差才能降至最低[8]。从图3中可以看出每份的面积由一个长方形（abcd）和一个三角形（ade）组成，则有：

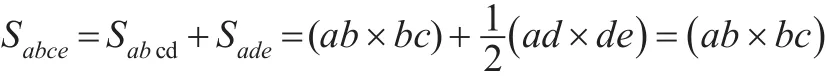
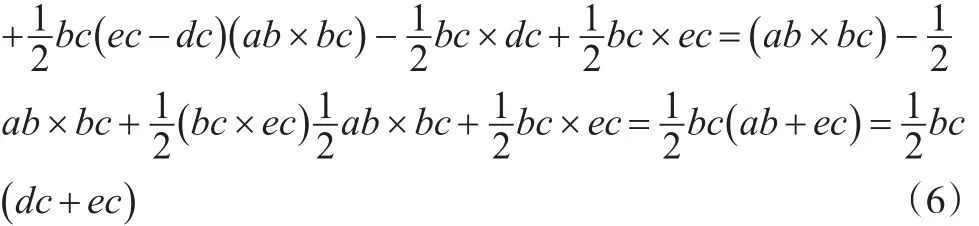
Y的面积由n个Sabce组成，即有：

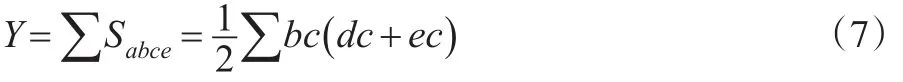
将式（7）与式（3）结合，则可以得出几何分组法的基尼系数：

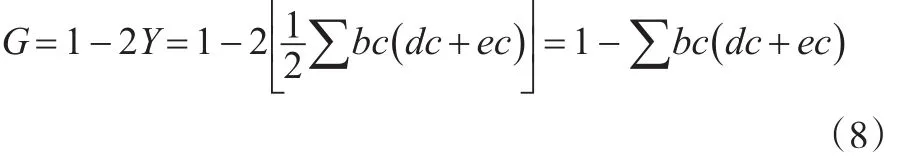
如果将式（8）中的度量单位转换为统计学意义，则有bc为组距，dc为组下限，ec为组上限，利用上述几个统计学指标，即可求得基尼系数。

1.3 积分法和几何分组法的计算结果比较

基尼系数的计算方法众多，但广泛运用的为本文研究的积分法和几何分组法，两种方法的计算方式不同，积分法适应符合函数规律的数据求解，而几何分组法能摆脱实际收入曲线（洛伦茨曲线）函数的限制，对数据特征依赖性不强。为验证两个计算方法的优劣性，选择某城镇居民的2017年收入分配数据为研究样本（见表2），对两种计算方法进行实证检验。

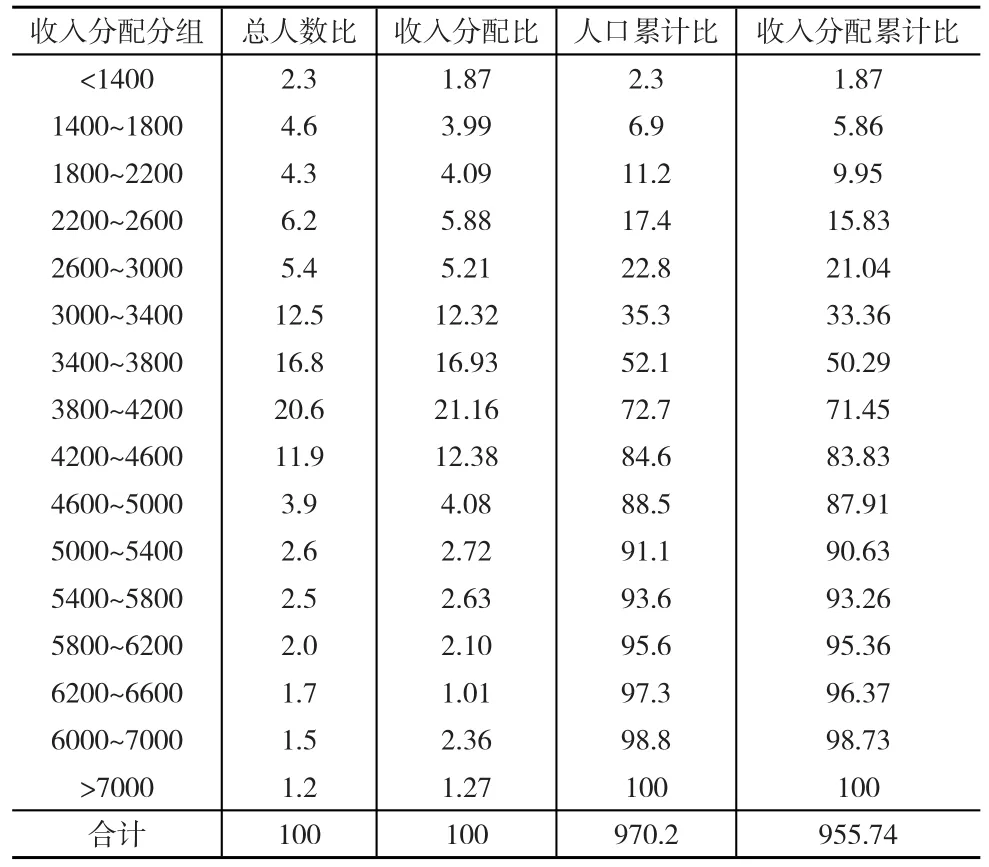
表2 某城镇居民2017年收入分配数据 （单位：100%）

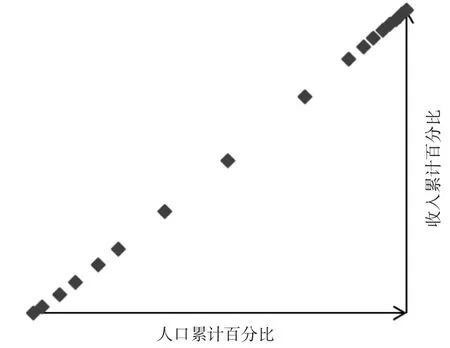
图4 某城镇居民2017年收入分配数据的函数分布规律散点图

如果使用积分法求解基尼系数，关键在于确定函数形式，将表2中的人口累计比和收入分配累计比散点分布用图4表示，以寻求二种数据间的函数关系。

从图4散点分布特征来看，人口累计百分比与收累计百分比之间存在y=axb函数关系。为验证该关系并求得常数a、b值，将所有数据代入y=axb函数，即可得到：

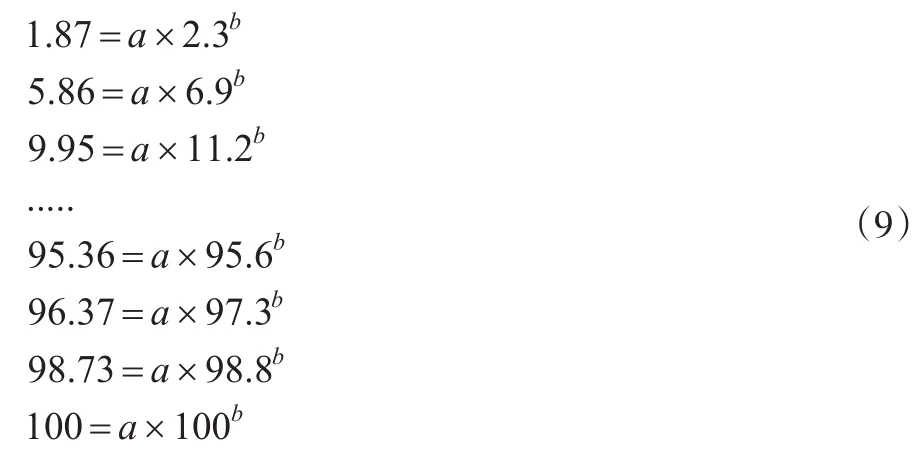
由式（9）求得a=0.7798,b=1.045,将a、b值代入积分法的基尼系数求解公式，则可得到：

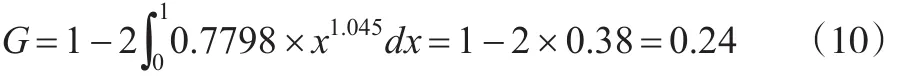
结果表明，积分法计算下该城镇2017年收入分配基尼系数为0.24，属于低水平的基尼系数区间。接下来使用几何分组法对2017年该城镇居民的基尼系数进行运算，由于原始数据已经分组完成，因此几何分组法只需要将数据代入公式（8）即可。

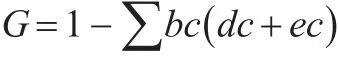
由此可见，积分法和几何分组法求解的基尼系数都为0.24，说明两种方法的准确率相似。但是积分法需要求解函数形式，对于数据的特征性要求更高，而且在实际操作中，寻找数据规律函数难度较大，在数据散点分布图中可能无法找到或无法确定函数形式。而几何分组法只需要将数据进行规律分组，无需依赖实际收入曲线（洛伦茨曲线）函数，对数据的规律依赖较少，适用多数实际性操作。而且几何分组法对数据按不同性质归类分组处理后，可以求解不同层次的基尼系数，便于研究不同层次的贫富差距等问题。

2 泰尔指数理论框架与实例计算

基尼系数对不平等程度反映较为准确，但存在二点不足。第一，基尼系数具有厌恶不平等现象，对穷人观察值较敏感，如果样本中穷人数据较大时，则基尼系数的计算结果误差偏大。第二，相同数量收入转移到研究样本时，基尼系数的结果可能全部转移至低收入样本，对计算结果有不利影响。因此，在计算不平等指数的相对性指标方法中，还有一类泰尔指数较为常用。泰尔指数由泰尔(Theil,1967)利用信息理论熵计算收入不平等而来，假设U为收入分配事件A的发生概率，即有p(A)=U,并且收入分配事件A发生信息量e(U) 服从的减函数形式，那么n个收入分配事件发生概率为U1、U2、U3……Un，并且在所有事件中，某收入分配事件一定会发生，即根据信息熵理论可得：

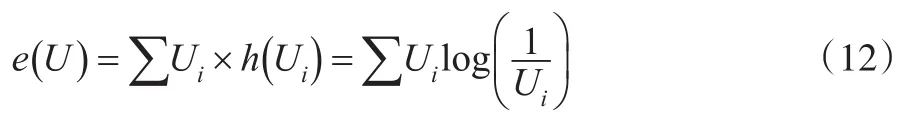
显然，当收入分配事件概率Ui趋近时熵值越大，泰尔认为可以用e（U）来反映收入分配不平等差距，依据信息熵理论e（U）值越大，收入分配越公平[9]，当n个收入分配事件中都有时，则表示n个收入分配事件达到了绝对公平，即e(U)=logn,泰尔在此基础上将定义logn-e(U)为泰尔不平等指数（T）。

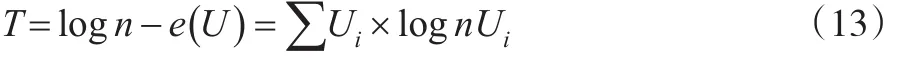
2.1 泰尔指数与广义熵指数的关系

由基本理论框架可知泰尔指数由信息理论熵指数演变而来，那么泰尔指数与信息理论中熵指数有什么关联呢？在信息理论中熵被定义为平均信息量，一般分布形式为连续和离散两种[10]，用公式（14）表示离散的广义熵指数,用公式（15）表示连续的广义熵指数。

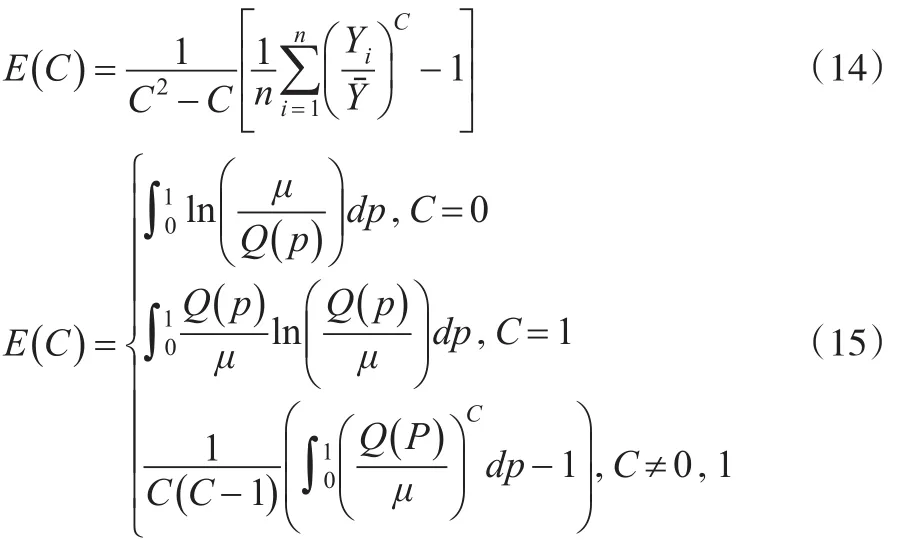
式（14）和式（15）中的C为常数，表示厌恶不平等程度，C值越大，表示厌恶不平等程度越小，Q（p）表示收入累计人口比对应的收入份配，μ表示收入平均值，p表示收入累计人口比。实际上泰尔指数是信息理论熵指数的特例，主要取决于常数C的取值，在离散型和连续型熵指数公式中，常数C不同取值代表不同的指数性质，具体见表3。

由表3可知，在离散型广义熵指数中，当C→0和C→1时，广义熵指数表示为泰尔指数，而在连续型广义熵指数中，当C=0和C=1时，广义熵指数表示为泰尔指数。

2.2 泰尔指数计算公式和计算实例

泰尔指数提出后，因其能够提炼相互独立的组间差异和组内差异，迅速被运用于不平等指数的计算。如果某区域内的收入和累计收入比等于人口和累计人口比，则表明该区域内的泰尔指数为0，收入分配达到绝对公平线。如果某区域内的收入份额较大，人口份额较少，则表明该区域内的泰尔指数趋近1，贫富差距较大，可见泰尔指数的取值范围也为[0,1]，这点与基尼系数有相似之处，甚至泰尔指数和基尼系数具有互补关系。基尼系数的计算方法众多，主要有积分法和几何分组法，而泰尔指数计算方法相对单一，目前国际上比较认同的主要为以下计算公式：

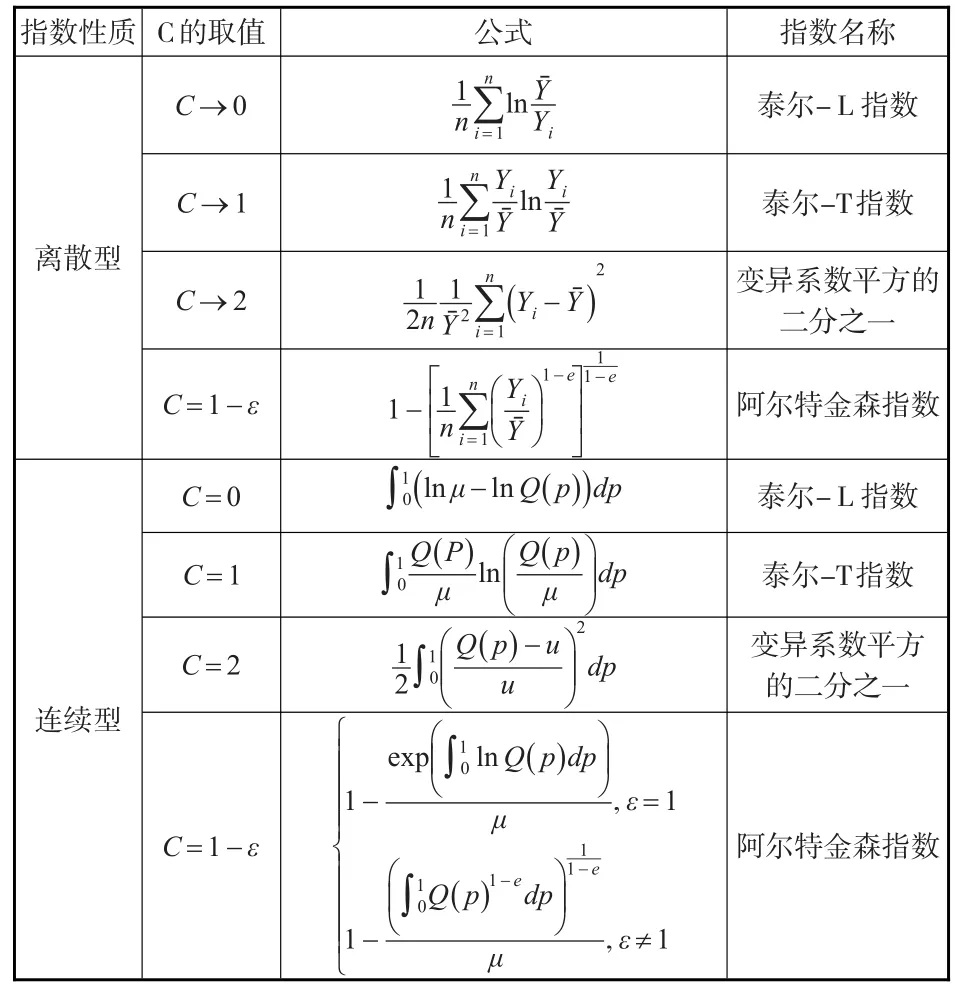
表3 不同C值下广义熵指数的性质

式（16）为总泰尔指数的计算公式，其中Y表示总收入份额，N表示总人口，Yij表示分组单元中的收入份额，Nij表示分组单元中的总人口。由于泰尔指数可以分解为若干个亚收入单元，因此还可以求得组间泰尔指数和组内泰尔指数，其计算公式依次为式（17）和式（18）。

式中Yi表示分组单元中第i个亚收入单元的收入份额，Ni表示分组单元中第i个亚收入单元的总人口。由上述公式可得到一个重要结论T=Tb+Tw，即泰尔指数为组间泰尔指数与组内泰尔指数之和，显然是一个加权后的泰尔指数结果，为体现未加权的泰尔指数关系，可以利用公式（19）计算收入单元内的未加权泰尔指数。

接下来利用沿海某市的人口数量、人均收入、省份总人口、省份人均收入为研究样本，测算该市在2008—2017年的泰尔指数，结果见下页表4。

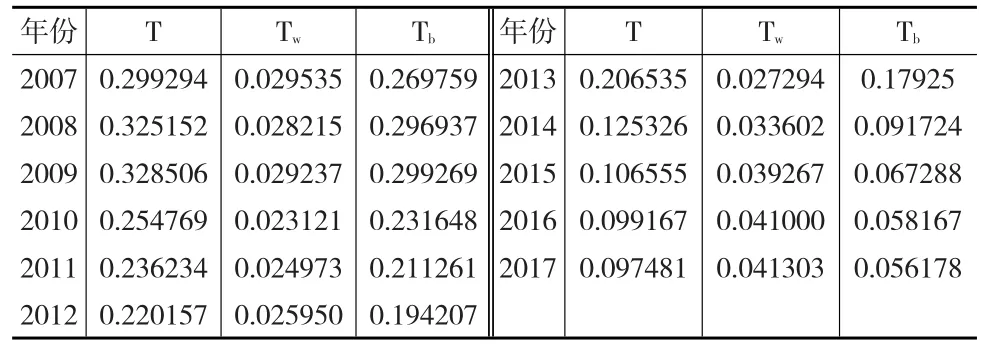
表4 某沿海城市2007—2017年的泰尔指数

由表4可知，总体泰尔指数T呈递减趋势，部分年份泰尔指数的增加未能改变递减趋势，证明在经济发展趋势利好的情形下，收入分配不平等现象正在逐渐降低，通过比较组内泰尔指数和组间泰尔指数的趋势变化，可以进一步佐证该现象。而泰尔指数的走向变化与经济合作与发展组织（OECD）最新公布的数据相吻合，说明泰尔指数在反映不平等程度具有较好的准确率。

3 不平等指数相对性指标对比

前文对基尼系数和泰尔指数的理论框架和计算方法进行了系统分析，但两者在不平等指数测算中实践差异如何，则可通过实际数据库进行验证。本文选择中国家庭动态跟踪调查（CFPS）数据库中的收入数据做样本[11]，时间跨度为2011—2016年，通过多次搜集反复验证，最终选择河南省为研究对象，并采取随机起点、等距抽样方法选取样本。本文侧重点为比较基尼系数与泰尔指数的优劣性，而非计算基尼系数和泰尔指数，因此本文并未区分样本数据中的城乡指标，统一按随机分配方式选择样本。考虑数据的可得性，样本数据以家庭为单位，主要以工资收入为指标，家庭经营性收入、投资性收入等被删除，最终样本量为1055户。为使对比结果具备科学性，对比方式分横、纵两种方式，纵向比较用2011—2016年的整体数据，横向比较用2015年月度数据。本文数据主要由Stata软件处理完成，结果除基尼系数和泰尔指数外，将变异系数和阿尔特金森指数一并列出。为便于比较所有结果精确到万分位，其中纵向比较结果见表5。

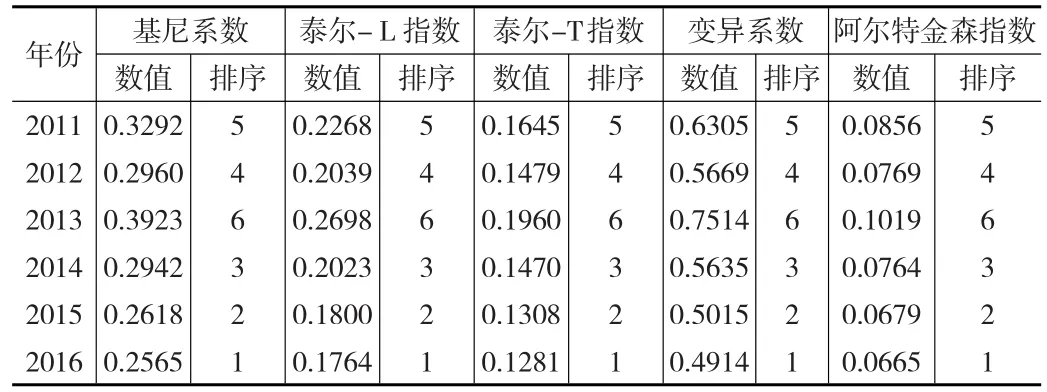
表5 2011—2016年不平等指数相对性指标的纵向对比结果

根据表5，基尼系数和泰尔指数的纵向比较结果类似，特别是排序结果基尼系数、泰尔指数、变异系数和阿尔特金森指数完全一样，证明不平等指数相对性指标方法具有一致性，对于不平等程度都具有解释能力。从基尼系数来看，2011—2016年间样本数据的基尼系数长期处于黄金分割律线0.382之下，说明样本数据中的收入相对较为平等，泰尔指数、变异系数和阿尔特金森指数佐证了该结论。但2013年几种测算方法的测算结果偏高，特别是基尼系数误差明显大于其他几种指标方法，甚至超过了黄金分割律线。研究样本发现，2013年样本中的低收入人群明显高于高收入人群，基尼系数的这种厌恶不平等性质，给基尼系数测算结果造成一定影响。而泰尔指数由于将收入群体进行分解，产生此类测算误差相对较少。那么是否说明泰尔指数优于基尼系数呢？选择较平缓的2015年月度数据作横向比较。由于连续月度数据相近且变化不大，为便于区分，只列出双月的测算结果，见表6。为对比，将变异系数和阿尔特金森指数一并列出。

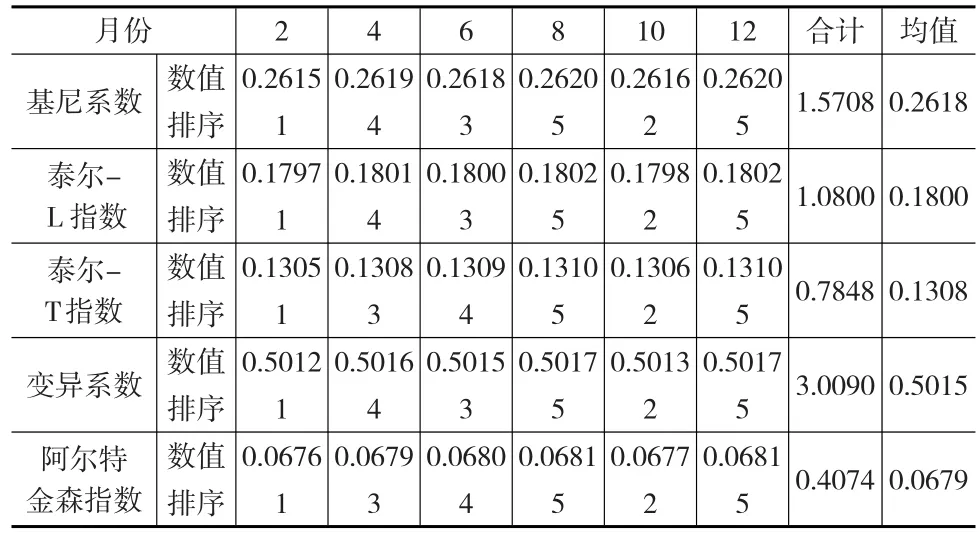
表6 2015年不平等指数相对性指标的横向对比结果

根据表6可知，2015年样本数据收入不平等现象并未发生较大变化，几乎是一个平静的波动过程，各指数的排序结果依然相似，只在个别月份出现微调现象，进一步说明不平等指数相对性指标具有一致性，在条件允许的情况下，可利用多种方法对不平等程度进行验证计算。从计算结果来看，几种相对性指标方法的均值结果约等于该指数全年整体值，说明不平等现象是一个积累过程。基尼系数在该轮验证过程中并未产生较大的误差，说明2013年过多的低收入人群对基尼系数计算结果产生了影响，在低收入人群占样本多数时，建议采用泰尔指数计算不平等指数的研究方法。同时在计算的过程中发现，样本数据6月至8月间中等收入和低收入人群有50%左右的位置更换过，基尼系数由于采用几何分组法，在分组的过程中很容易发现已更换位置的样本。但泰尔指数没有该步骤，即使样本个体位置变动也未被发现。由此可见，泰尔指数与基尼系数相比，泰尔指数无法体现收入位置的变动现象，即使高低收入人群全部进行互换，所得的泰尔指数相等。在研究收入位置变动的不平等指数时不适合采用泰尔指数，而应选择基尼系数。

4 结论与讨论

不平等指数反映社会贫富两极人口的分布特征，对社会和谐发展具有重要的指导作用。学术中将计算不平等指数方法分为绝对性指标和相对性指标，绝对性指数的计算方法简单，但受量纲限制，对单位变化后的不平等指数计算不准确，因此本文在相关研究的基础上认为相对性指标要优于绝对性指标。相对性指标方法众多，比较常用的有基尼系数、泰尔指数、相对平均离差等，如何选择相对性指标方法是本文的重点。通过对比发现基尼系数和泰尔指数是较为成熟的两种方法，对不平等指数具有较好的解释能力。

本文通过系统的几何分解基尼系数和推导泰尔指数后发现以下几点问题。

（1）基尼系数的计算方法众多，比较常用的有积分法和几何分组法，积分法能够较为简单的求得基尼系数，但对数据的规律性要求较高，求解实际收入线（洛伦茨曲线）函数的工作量无法预测，因此积分法的实际操作性不强。几何分组法可依据已知数据，对数据库进行规律性的分组，尽管计算量较大，但可操作性强，相对而言，几何分组法是实际基尼系数计算过程的重要方法之一。另外，几何分组法中存在以直代曲的步骤，是计算结果误差的主要来源，因此，几何分组法计算下的基尼系数是误差值，并不是实际基尼系数值。（2）值得注意的是本文只针对不平等指数相对性指标中的基尼系数和泰尔指数进行了比较，变异系数、阿尔特金森指数只列出了相关结果，仅仅起对比作用，实际上变异系数、阿尔特金森和泰尔指数与熵指数的有着密切的关系，广义熵指数是他们的特例，而基尼系数则与熵指数没有关系，因此不能将基尼系数归类于熵指数。（3）尽管基尼系数不同于泰尔系数，但两者之间具有一定的互补性。首先二者的取值区间都为[0,1]，对于同一样本数据，基尼系数和泰尔指数的变化趋势类似。其次，面对不同不平等指数计算时，可依据样本数据特征进行选择，比如基尼系数具有“厌恶不平等”现象，对低收入人群较为敏感，当低收入样本数据较大时，选择基尼系数会加大计算结果误差，此时可选择泰尔指数替换基尼系数。当研究收入变动的不平等指数时，由于泰尔指数无法体现样本数据的收入变动现象，如果使用泰尔指数反映此类问题则可能得到错误的变动结果，此时可选择基尼系数替换泰尔指数。