农业经济调查缺失数据的贝叶斯和Bootstrap多重插补的比较

熊 巍，潘传快，祁春节

（1.华中农业大学 经济管理学院，武汉430070；2武汉纺织大学 经济学院，武汉430200）

1 问题的提出

对农业、农民、农村问题的研究很多都需要开展农业经济调查以获取数据。理想的情况是这些数据都是完整无缺失的，但其实是很难做到的[1]。通常情况下，农业经济研究人员遇到缺失值都会采取成列删除的方法，即作为无效数据删除所有含缺失值的个案，留下完整数据作为分析[2]。即使农业研究人员忽略了这个问题，但在大部分分析软件中，为了数据分析得以流畅进行，都会自动成列删除缺失数据[3]。如果数据的缺失比重很低，并且是完全随机缺失（MCAR），成列删除相当于在损失很小的情况下得到一个完整数据，而且这个完整数据还是原样本的简单随机子样，就意味着用该数据估计是无偏的[4,5]。但遗憾的是农业经济调查的缺失比重一般较高，而且很多时候即使缺失比重不高，但变量太多，采取成列删除也会引起很大的数据损失[4]。此外，数据缺失往往不是完全随机的，比如产量越高的种植户越不倾向于透露自己的产量，那么成列删除后的数据就是有偏的。所以在处理农业经济调查缺失数据时，删除一般都不是最好的处理方法[6]。更值得推荐的方法是不删除任何数据，而结合数据的经验分布，对其缺失部分进行插补[7]，或对含缺失值的数据进行最大似然估计[8]。插补特别是多重插补由于能更精准地估计模型参数而更多地被采用[9]。因为多重插补可以利用同一缺失值不同填补值之间的差异来抵消估计和检验误差的减少，使估计检验更准确[10]。特别是当农业经济研究人员不需要数据本身，只需要根据数据建立农业经济计量模型以完成研究。一个基本的多重插补思想是将根据完整未缺失数据的均值或回归值加上均值为0的“白噪声”干扰，但其插补值的离散程度仍然偏低，因为利用该方法的模型参数是固定的[11]。可以利用贝叶斯法和Bootstrap法让回归参数随机化，贝叶斯法的基本思想是让插补模型参数来自其后验分布的一个随机抽取[12]，而Bootstrap法的基本思想是让线形模型的参数来自原完整样本的多个Bootstrap样本[13]。Bootstrap法跟贝叶斯法相比，可以不需要两个步骤：Choleski分解和从χ2分布中抽取以完成残差估计，因此效率上会更高一点。

本文主要对一元线性模型下贝叶斯多重插补和Bootstrap多重插补进行比较。作为实证分析案例，本文选取在中国柑橘主产区对种植户所做的调查数据，分别利用两种方法对缺失值进行多重插补，再汇总计算农业经济计量模型所需要参数的估计和检验结果并加以比较。本文所有的数据分析均使用R程序语言软件。

2 模型和方法

2.1 假设

为了方便两种方法的比较，本文的插补模型和方法基于以下假设：

（1）目标缺失变量为单一变量Y且呈正态分布，而用以辅助插补的完整变量X可以是多元的，但仍成正态分布。如果数据中存在多个变量缺失，那就分解成多个插补模型，即每一个缺失变量构建一个插补模型。

（2）目标变量Y为随机缺失（MAR），即Y的缺失跟本身未观测值无关，但跟辅助变量X有关。这意味着只要借助辅助变量而不需要借助缺失变量来完成对缺失值的插补。

（3）Y跟X之间显著存在正态线性相关关系，即：

式（1）中，β为回归系数，是一个q维向量，而σ2为残差标准误差，也即插补模型随机干扰项的平方。

2.2 贝叶斯多重插补

农业经济调查数据由缺失变量Y和未缺失变量X构成，如果未缺失变量不唯一，则X为矩阵。Y有n1个未缺失的观测值记为Yo，其对应的X部分记为Xo；其n0缺失值记为Ym，其对应的X部分记为Xm。根据式（1），利用数据的未缺失部分Yo和Xo，可以获得模型的最小平方估计和：

其中为模型回归参数向量，而残差方差估计值为：

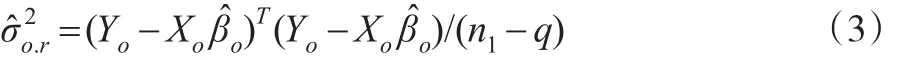
根据贝叶斯思想，β和的后验分布可由构建，其中的后验分布为χ2分布：

而基于的β的条件后验分布为正态分布：

缺失变量的每个缺失值Ym可以采取以下模型产生任意多个插补值：

式（6）中，为根据式（4）确定的后验分布的任意个随机抽取，而来自式（5）给定的后验分布的任意个随机抽取，Z1为n0个标准正态分布值。即：

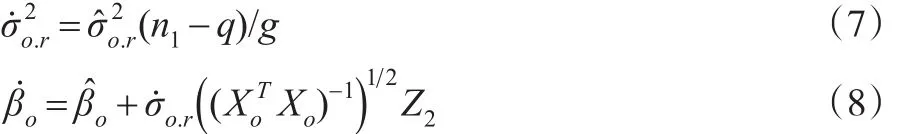
式（7）中，g是来自χ2(n1-q)分布的一个随机值；式（8）中Z2为q个标准正态分布随机值为的Cholesky分解。

2.3 Bootstrap多重插补

Bootstrap多重插补的一个核心思想是，让插补模型的回归参数来自Bootstrap样本的估计，由于Bootstrap样本不唯一，所以根据每一个Bootstrap样本估计的参数也不唯一。设(Yb，Xb)为来自观测部分(Yo，Xo)一个的Bootstrap样本,其容量为n1。根据该Bootstrap样本，模型参数的最小平方估计为：

而残差方差的估计为：

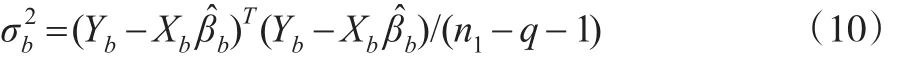
根据式（9）和式（10），可以利用以下模型产生缺失部分Ym的任意插补值插补：

式（11）中，Z1为n0个标准正态分布值。

2.4 汇总估计方法

（1）插补次数的选择

多重插补的思想是利用对同一缺失值的多次插补来弥补估计标准误差的损失，那么需要多少次的插补才能弥补这种损失呢？从理论上来说，插补次数越多估计越准确，如果插补次数趋于无穷大，估计标准误差的估计几乎是完全准确的。但是在实际上，这意味着巨大的计算量，纵使对计算机而言，如果插补次数设定很大计算量也是惊人的。很多研究显示，当插补次数超过10次时，对估计标准误差的改进已经非常有限，因此在实际操作中，只要将插补次数设定为5～10次即可。

（2）多重插补的点估计

假设在一次农业经济调查中建立农业经济计量模型所需要的总体参数为θ，θ可以是单一的标量或者是向量，取决于感兴趣参数的个数，比如想知道农户的平均家庭收入θ=μ。多重插补后θ的汇总估计为：

式（12）中，m为插补次数对，而参数的内部方差：

其中，Uj为插补后数据的的协方差矩阵。而同一缺失值不同插补值之间的方差为：

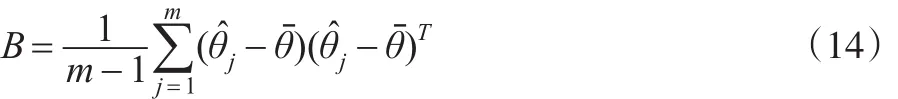
式（14）中，m-1为自由度。因此估计参数θ的总方差为：

式（15）为有限次多重插补的参数方差计算公式，并不精确，可以用下式进行调整：

（3）多重插补的区间估计和检验统计量

统计量ˉ符合一个自由度为νnc的Student-t分布：

式（17）中，自由度νnc的计算方法为：

根据式（17），θ的一个置信水平为(1-α)的置信区间为：

式（19）中，tα2(νnc)为Student-t分布在自由度νnc下的第100(1-α/2)分位数。

在检验时，θ的检验t值如下：

其对应的P值为：

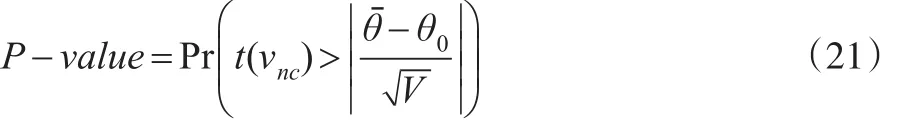
如果利用方差分析检验模型参数的显著性，则F检验统计量构建如下：

其相应的P值为：

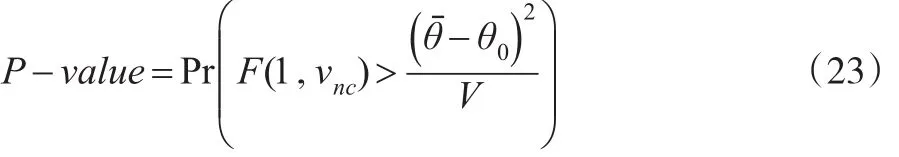
3 实证分析

本文的实证数据为国家现代农业产业技术体系（柑橘）团队在中国柑橘主产区开展的一项调查。调查内容为柑橘种植户的柑橘生产销售成本收益，调查对象为主产区的柑橘种植户，调查方式为入户访问调查，调查问卷以开放性问题为主，调查样本为调查工作人员筛选后的典型种植户。

3.1 缺失信息

本次调查搜集的数据较为庞大，由于篇幅所限和分析需要，本文选取其中的部分典型变量来进行实证分析，选取的这些变量中既有完整数据也有缺失数据，而且变量之间普遍存在相关关系，这些变量的部分数据显示在表1中。

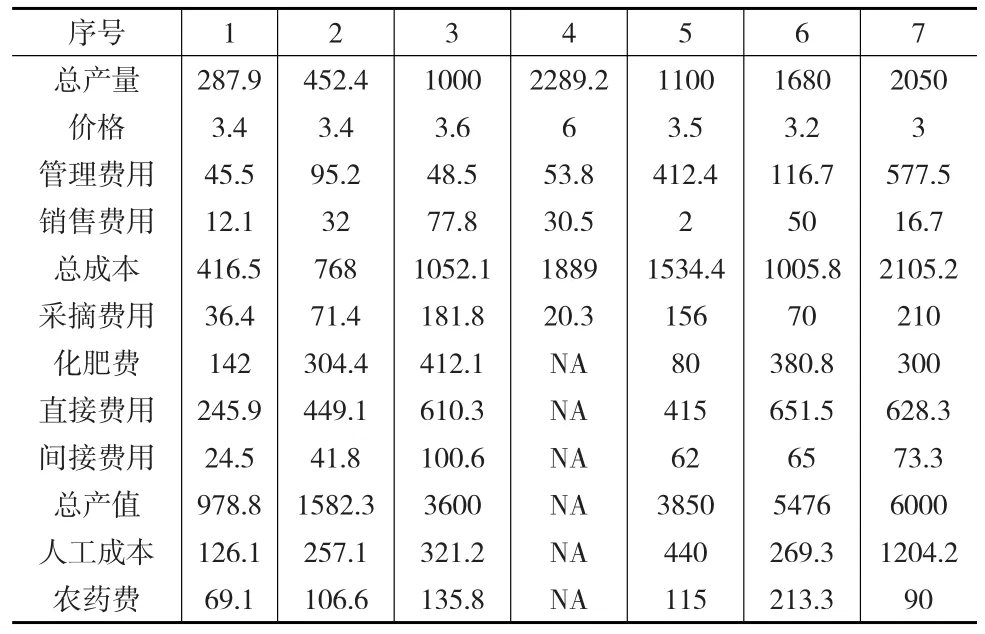
表1 选区的变量的部分单元数据

为了在R中运行，在表1中将缺失值表示为“NA”即为缺失值（Not Available）。表2进一步描述了这些变量的缺失信息。

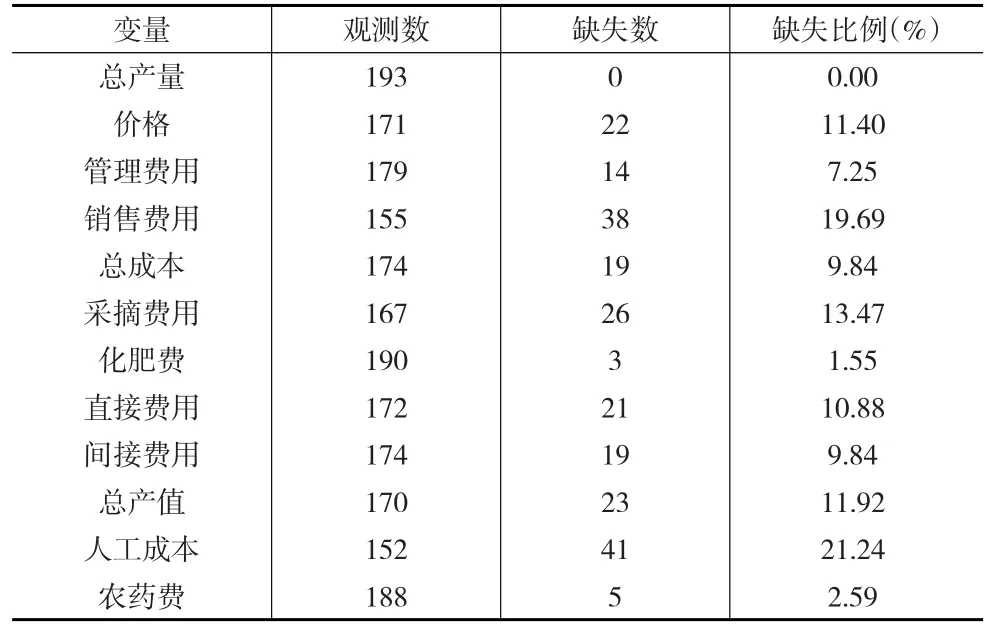
表2 每个变量的缺失信息

从表2可以发现，除了总产量以外，所有的变量都有缺失，但是有些变量缺失比重很高，比如销售费用和人工成本，而有些变量缺失比重非常低，比如农药费和化肥费用，其他变量的缺失比重居中。

3.2 辅助变量选择

本文选取总产值为目标缺失变量，按照模型假设辅助变量必须是完整的，但该数据只有总产量一个变量达到要求，为了提高插补的准确性，再将缺失比例较低的化肥费用和农药费用加进来。这两个变量为数不多的几个缺失值用各自的简单随机抽取进行单一插补，插补效果如图1所示，图中“×”表示插补值。

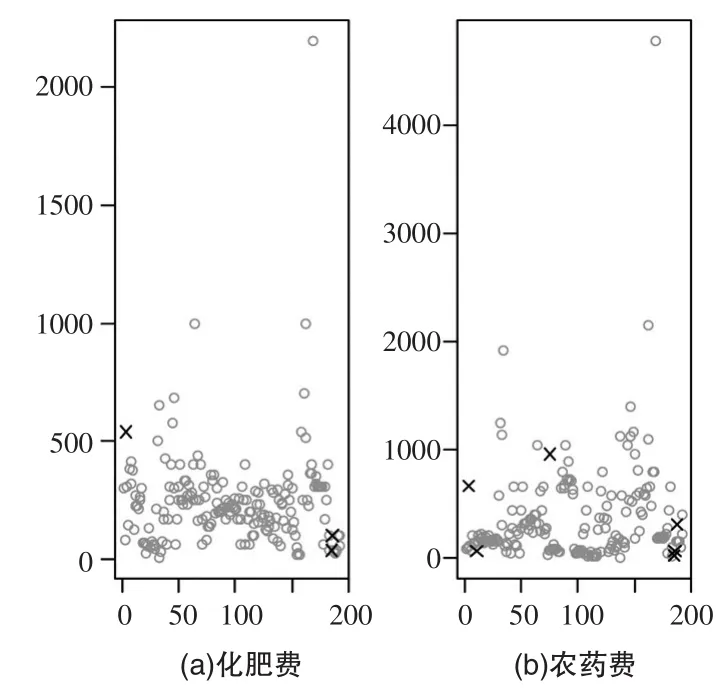
图1 农药费和化肥费的简单随机插补

为进一步考察目标缺失变量和辅助变量之间的相关关系，将这4个变量的完整部分数据绘制成相关散点图,如图2所示。从图中可以发现，4个变量均成正态分布，基本符合正态假设，只是由于数据来自典型种植户调查，而这些典型种植户有很多是种植大户，因此分布明显右偏。虽然极端值存在且破坏了相关关系，但从图中仍可以看出，各个变量之间存在线性相关关系，也基本符合假设需要。

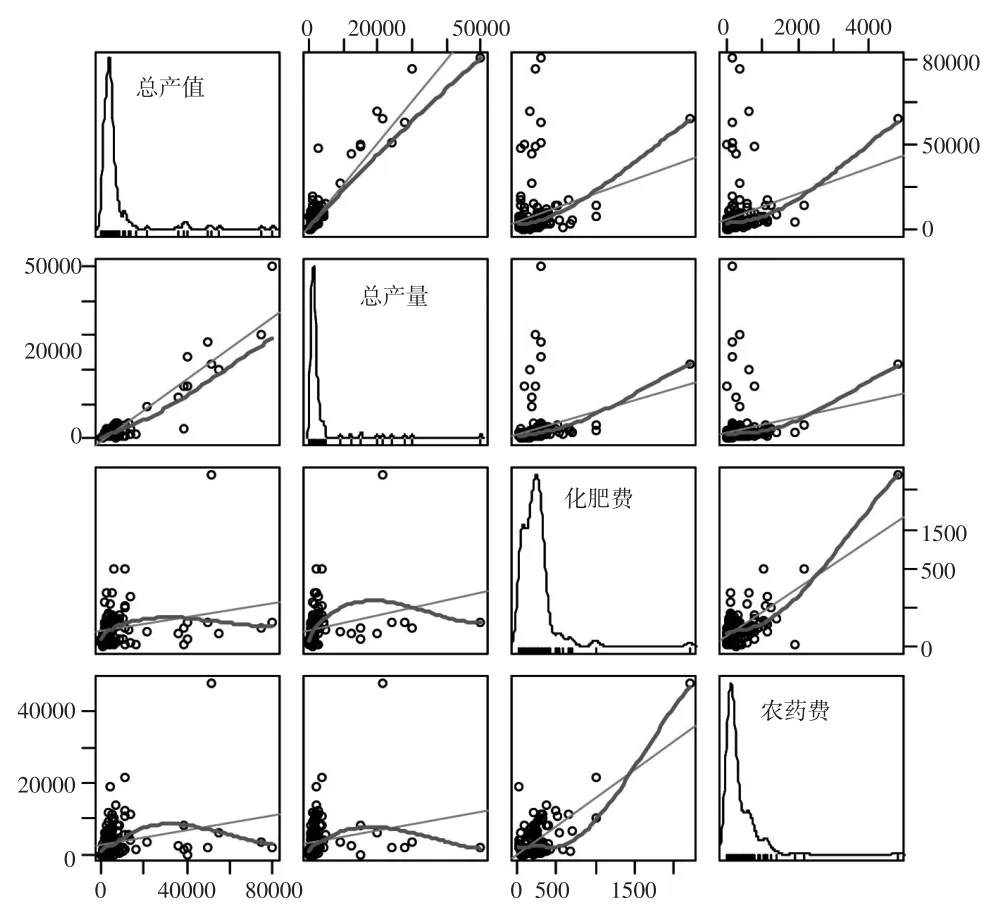
图2 变量之间的相关散点图矩阵

3.3 多重插补

现利用R编程，采用贝叶斯法和Bootstrap法对缺失数据进行多重插补，然后估计经济计量模型的参数，事先假定该经济计量模型为总产值关于化肥费用、农药费用以及总产量的线性回归模型。表3为采取贝叶斯多重插补后估计的模型参数以及相应检验。

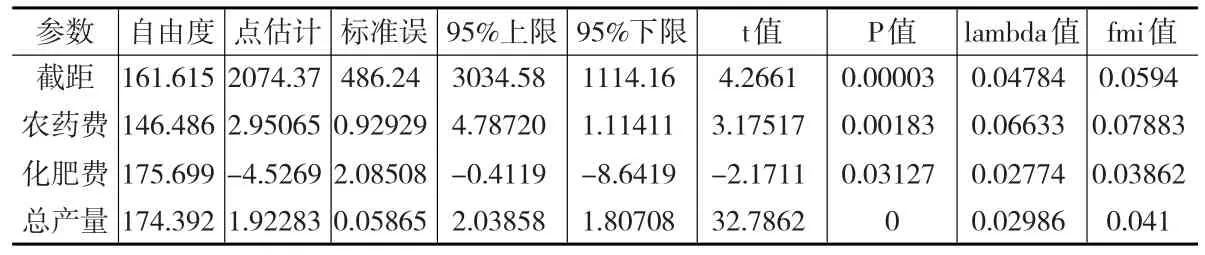
表3 贝叶斯多重插补后数据的估计检验结果

根据贝叶斯多重插补的分析结果，可以得到如下农业经济计量模型：

总产值=2074.37+1.92283×总产量-4.5269×化肥费+2.95065×农药费

表3不仅给出了该模型参数的点估计和区间估计，还给出了标准误差、检验t值和P值。表中的lambda值和fmi值表示因缺失比重的增加而增加的误差。作为比较，再将该缺失数据利用Bootstrap法进行多重插补，其模型的估计检验结果展示在表4中。

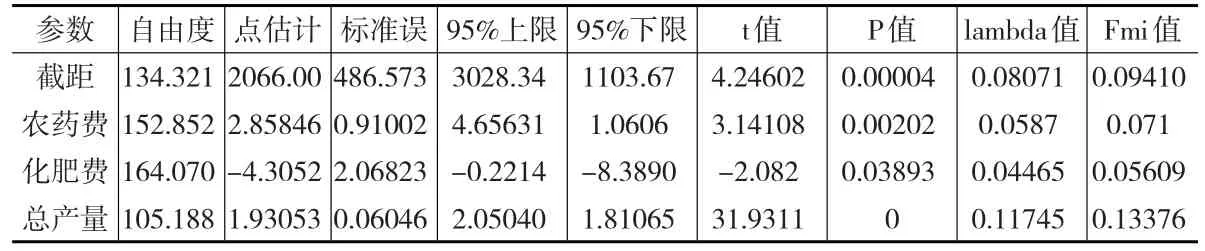
表4 Bootstrap多重插补后数据的估计检验结果

根据Bootstrap多重插补的分析结果，可以得到如下农业经济计量模型：

总产值=2066.00+1.93053×总产量-4.3052×化肥费+2.85846×农药费

3.4 比较分析

通过表3和表4的比较分析，采取贝叶斯法和Bootstrap法多重插补后的参数点估计区别非常小，几乎可以忽略，估计量的标准差也非常接近，检验的t统计量也差别很小，从这点上来看两者似乎没有太大的差别。但可以发现两者对自由度的估计差别还是很大的，采用贝叶斯法估计的参数自由度似乎比Bootstrap法估计的自由度大（农药费用对应的自由度除外），说明贝叶斯法的估计更可靠些（有更大的样本支持），从检验P值上也可以看出，在相同的t值水平下，采用贝叶斯法由于更大的自由度，P值更偏小些，从区间估计上看也具有更窄的置信区间，说明同等置信水平下估计的准确性更高。

两者的fmi值以及λ值区别不大，可以看出由于目标变量缺失的比例不高，因此由于数据缺失而引致的回归模型额外方差比重并不算高。

4 结论

在缺失模式为单一缺失、缺失机制为随机缺失（MAR）的条件下，假设缺失变量和辅助变量的后验分布为正态分布，彼此关系为线性关系，那么就可以构建一元正态线性多重插补模型。在该模型下，通过两个方面来增加插补值的离散型，一是为插补值加入随机干扰项，二是让模型参数随机产生。模型参数的随机产生方法有两种：贝叶斯法和Bootstrap方法，两者产生随机参数的思想截然不同。

根据对中国柑橘主产区的种植户的入户调查数据的实证分析发现，虽然贝叶斯法和Bootstrap法的思路不同，但最终根据两者构建的农业经济计量模型的点估计结果却差异很小。不过值得注意的是，虽然点估计结果差别很小，但是两者对参数自由度的估计却差别较大，采用贝叶斯法估计似乎有更大的自由度，也就意味者有更准确的区间估计和更显著的检验效果。但是从效率上说，Bootstrap方法会更有优势一点，因为其比贝叶斯法省了两个步骤，使计算机编程的难度降低。此外，跟成列删除相比，插补虽然没有损失信息，但加入了额外信息，这需要充分验证缺失值插补模型是否符合假设，否则其插补效果甚至不如删除。