基于辅助粒子滤波与灰色预测的时间序列NAR模型状态估计
2019-03-14马雪莹蔡如华宁巧娇吴孙勇
马雪莹,蔡如华,宁巧娇,吴孙勇
(桂林电子科技大学 数学与计算科学学院,广西 桂林 541004)
0 引言
时间序列预测在很多领域有着极其广泛的应用。对于如何进行时间序列的建模和预测,尤其是线性模型,这方面的研究由来已久,常见的方法有AR模型、最小二乘估计等。但现实中,有很多时间序列的数据是大量的,并且具有非线性的特点,上述方法便不再适用。于是,统计学家们提出了人工神经网络、支持向量机方法等,但是神经网络只适用于短期预测,支持向量机方法计算时间较长,计算过程复杂[1,2]。粒子滤波方法是近年提出的一种适用于视觉目标跟踪的有效算法,该方法简单易行,适用于任何非线性非高斯环境[3]。在非线性时间序列建模过程中可以利用粒子滤波算法,分析解决复杂的积分问题,避免了非线性时间序列分析过程中需要储存大量历史数据的问题,该算法在降低算法复杂度、提高拟合性能上具有一定的优势。
利用粒子滤波(PF)方法估计非线性自回归(NAR)模型的状态,在一定程度上提高了估计的精度,但是粒子滤波方法在计算过程中,容易出现粒子退化现象,增加了由参数估计带来的估计误差[4,5]。辅助粒子滤波(APF)可以自然地从当前量测中产生样本,使之更可能的落在高似然区域内,降低了滤波对外部干扰的敏感度,而灰色预测在不增加计算量的情况下可以对目标状态进行预测,克服粒子退化现象。
本文在NAR模型建模的基础上,利用辅助粒子滤波和灰色预测相结合的方法估计NAR模型的参数和状态,并应用于股票数据的预测和分析。仿真实验及应用实例表明,该方法比传统NAR及粒子滤波方法的效果更好。
1NAR模型
NAR模型是一个时间序列预测模型,主要利用时间序列数据估计未来的预测值,一般使用最小二乘法确定模型的参数和结构[6-8]。NAR模型可以表示为:

其中x(t)为时间序列数据,np为多项式展开的项数,Pl为l阶回归项向量,且P1=1,θl为l阶回归参数,ε(t)为白噪声。
式(1)可用矩阵形式表示为:

其中P是一个n×m的回归项量矩阵,θ是一个m×1的系数向量,ε为白噪声残差。利用QR分解方法分解式(2)中的矩阵P,即:

其中Q为正交矩阵,R为上三角矩阵。定义g:

则:

若P中每一列的误差为ei,基于已定义的g,每一列i的误差值可表示为:

通过观察发现的值越大,模型残差越小,因此可根据式(6)选择出对模型有意义的回归项PM=QMRM,其参数值θM可以通过对式(3)和式(4)利用QR分解方法分解,由式(5)计算得到,记为
通过上述方法可得到NAR最佳模型:

2 辅助粒子滤波与灰色预测的状态估计
2.1 辅助粒子滤波
辅助粒子滤波是标准粒子滤波的一种扩展[9,10]。其中粒子滤波是基于序贯重要性采样(SIS)思想,利用蒙特卡罗(MC)和执行贝叶斯递归估计的一种滤波方法。SIS滤波的基本思想是从概率密度函数p(x)中采集样本,利用带有权值的样本表示后验概率密度,从而得到目标的状态估计。其基本算法为:
令k时的联合后验密度近似为:
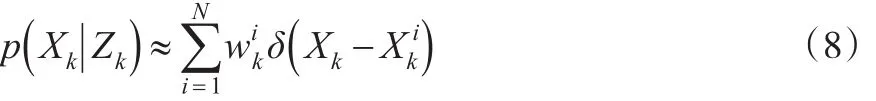
通过增加的样本和新状态获得新样本,并得到权重的更新方程:
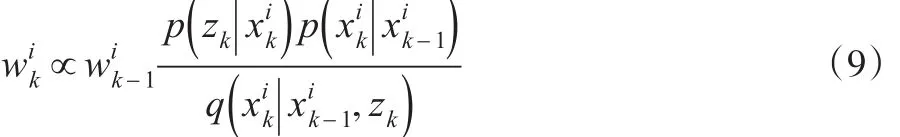
则后验概率密度可近似为:

但是重要权重的方差会随时间增长,在若干次递归后,每个粒子几乎都会带有很小的权重,产生权重退化现象。为了改善这种现象,需要引入重采样方法。
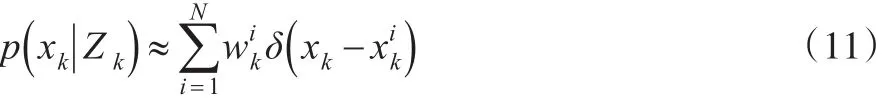
引入重采样算法的SIS滤波构成了基本的粒子滤波算法。但是由于重要性密度是独立于量测zk的,所以这类滤波对外部的干扰是低效且敏感的,并且随着重采样的进行,粒子的多样性会丧失,为了解决这一问题,提出了辅助粒子滤波。
辅助粒子滤波的主要思想是在粒子转移到k时刻之前在k-1时刻实现重采样,主要源自SIS中引入一个重要性密度并且这个重要密度可以导出样本集,其中ij表示粒子在k-1时刻的标记。但是APF的采样获取主要来自于联合密度,这样就可以忽略(xk,i)中的标记i,从联合密度中产生采样用来刻画新采样的重要性密度函数定义为:
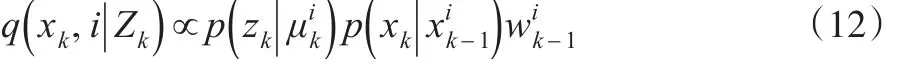
其中μ是在xk-1已知时的xk的信息。均值可以看成的一个样本值,所以式(12)可改写为:
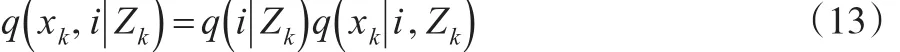
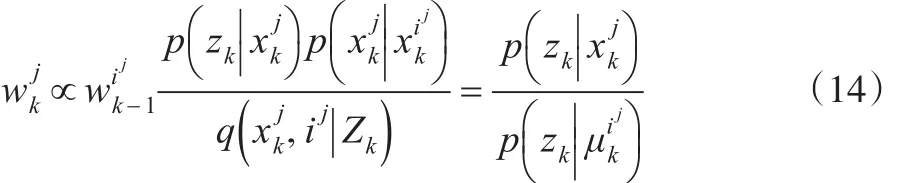
则可得到其状态估计值:

2.2 灰色预测原理
灰色预测方法先由历史数据构建一个序列,通过累加运算(AGO)生成一个累加序列,构建灰色微分方程并利用该累加值估计方程参数,从而预测下一时刻累加值,最后通过逆累加(IAGO)作用于累加预测值,得到目标状态的预测值[11,12]。
利用灰色GM(1,1)进行建模:
(1)构建一个包含最近量测信息的序列X(0)=式中x(0)(n)为量测数据,n为序列长度。
(2)通过对X(0)进行累加运算(AGO)建立一个新序列其中
(3)构建灰色微分方程:

其中a,b是微分方程的系数。
其中z(1)(k)为均值生成序列且
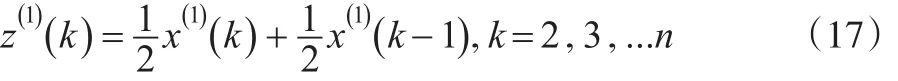
由最小二乘法得到系数a,b的值。
把系数a,b带入,即可得到1-AGO灰色预测模型:
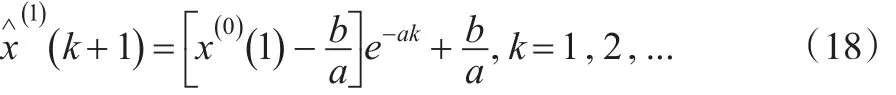
因为1-AGO灰色预测模型为一次累加数据得到的,所以需要将通过逆累加(IAGO)还原成状态预测值,即有:
2.3 NAR模型状态估计
辅助粒子滤波进行了两次加权操作,考虑了当前量测对状态估计的影响,生成的粒子权值变化更稳定,使模型更加接近未知的状态,估计的结果也更加准确。而灰色预测模型主要是在利用粒子滤波对当前的目标状态进行估计的基础上,再把目标历史序列和当前目标状态作为输入信息,利用灰色预测理论对下一时刻的目标状态进行预测,在不增加计算量的情况下,进一步改进粒子退化现象,提高预测效果。于是把辅助粒子滤波和灰色预测方法结合在一起对时间序列的NAR模型状态进行估计,得到以下状态估计的基本步骤:
(4)判断k大小:若k+1≥f(f为灰色系统输入的粒子数),则进行灰色预测算法,反之进行辅助粒子滤波算法。
为了更准确地评价NAR、PF-NAR、APFGM-NAR状态估计方法的好坏,将采用平均绝对误差(MAE)、平均绝对百分比误差(MAPE)、均方根误差(RMSE)三个评价指标:
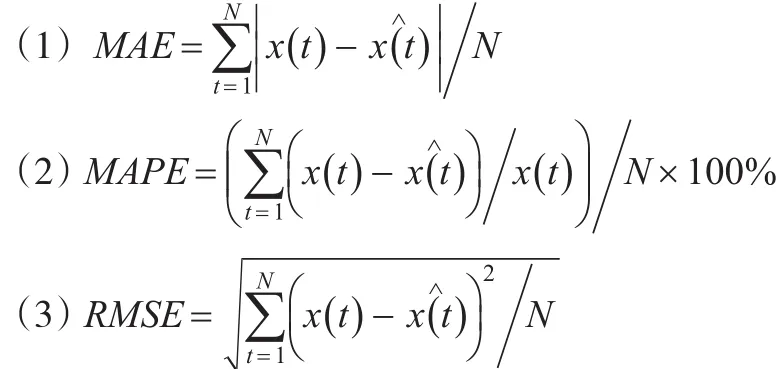
3 仿真实验与应用实例
3.1 仿真实验
为了验证基于辅助粒子滤波及灰色预测对NAR模型状态估计的可行性及优越性,需要建立一个NAR模型,即:
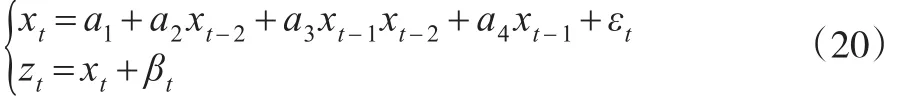
其中xt为状态向量,ai为模型系数,由最小二乘法可得ai值分别为-0.5536,0.7064,0.9966,1.4549,εt为高斯白噪声,zt为量测向量,βt为量测噪声。
由式(20)可以得到模型的状态与量测图形,如图1所示。
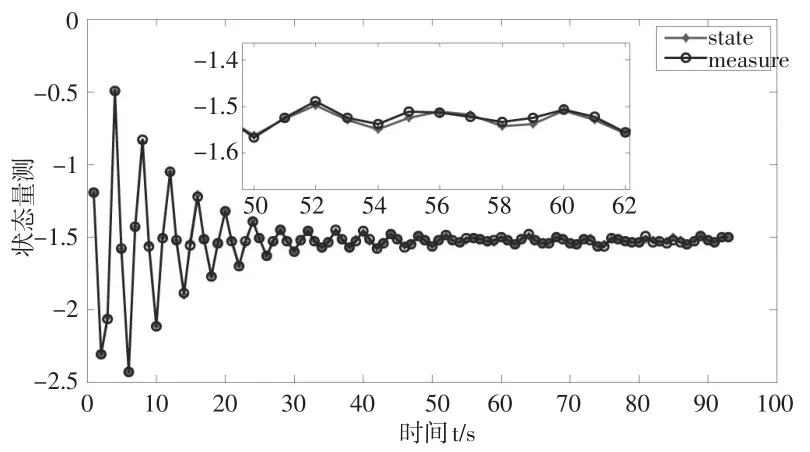
图1 状态与量测图
通过式(20)中的状态方程与量测方程进行粒子的传播与更新,得到NAR模型的状态估计值,并与传统的NAR和PF-NAR方法的估计结果作比较,如图2所示。
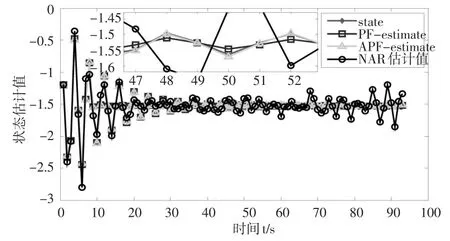
图2 APFGM-NAR、PF-NAR和NAR状态估计图
在得到NAR估计值,PF-NAR估计值与APFGM-NAR估计值后,通过残差计算公式得到残差估计值并进行对比,如图3所示。
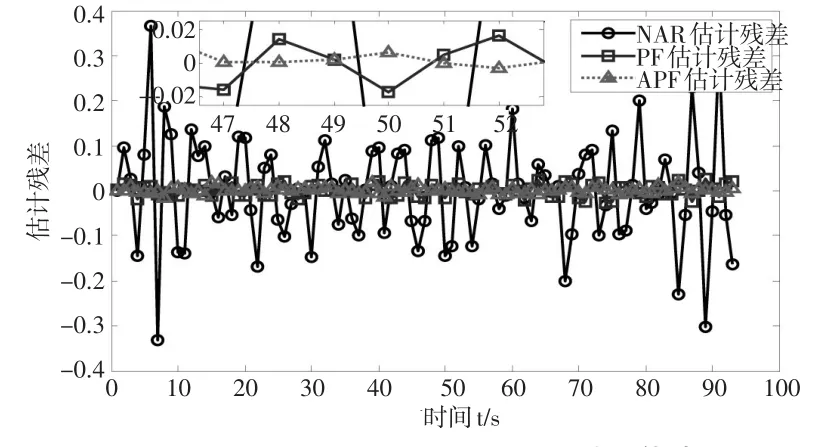
图3 APFGM-NAR、PF-NAR和NAR残差估计图
通过对图2的观察可知,由APFGM-NAR方法得到的状态估计值比传统的NAR和PF方法更加接近真实的状态,因此可以说明由APFGM方法估计NAR模型的参数和状态是可行的。对图3分析可知,APFGM-NAR方法所得到的估计残差值在零均值附近波动且与其他两种方法相比波动较小。为了更好地对比三种方法的估计精度,利用MAE、MAPE和RMSE三种评价指标对估计结果进行评估,结果如表1所示。从表中可以看出APFGM-NAR方法的估计精度最高。

表1 APFGM-NAR、PF-NAR和NAR性能评价指标
3.2 应用实例
本文选取深深宝A股票,提取2014年12月23日至2015年6月12日的115个交易日的收盘价,数据来源通达信金融终端软件。深深宝A股票的时间序列如图4中ture-state所示,通过对图中股票收盘价的走势分析,可以发现其具有很强的非线性,由此,可以把115个交易日的收盘价当做仿真数据,通过上文建立合适的NAR模型,并对模型进行状态估计,如图4中NAR-state所示。观察图4可知,NAR状态估计与真实状态之间的误差较大,因此利用辅助粒子滤波与灰色预测相结合的方法估计NAR模型的参数和状态,并与基于粒子滤波方法的估计结果作比较。
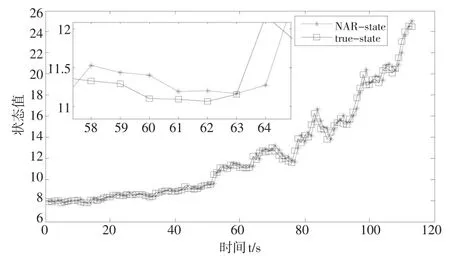
图4 深深宝A股时序和NAR状态估计图
利用辅助粒子滤波与灰色预测相结合的方法估计NAR模型的参数及状态,与粒子滤波估计结果进行对比,如图5。并对两种方法的估计结果进行残差计算,得到残差对比图,如图6所示。
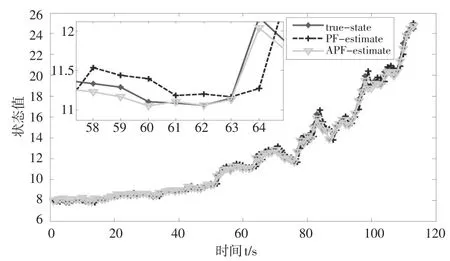
图5 APFGM-NAR和PF-NAR方法的股票价格估计
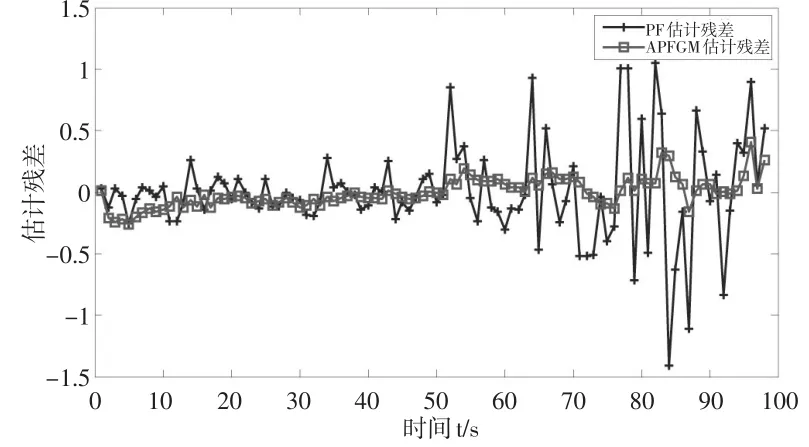
图6 APFGM-NAR和PF-NAR方法的残差估计图
由图5可知基于辅助粒子滤波与灰色预测的方法对NAR模型状态的估计比粒子滤波方法更加接近于真实的状态。由图6可知,基于辅助粒子滤波与灰色预测方法的估计残差比粒子滤波估计残差在0均值上下的波动幅度小,更平稳。为了更加直观地比较这两种方法对股价走势预测的效果,根据性能评价指标,给出了两种方法的MAE、MAPE、RMSE的对比值,如表2所示。

表2 APFGM-NAR和PF-NAR性能评价指标
通过对以上图表的观察分析可知,基于辅助粒子滤波与灰色预测的方法比粒子滤波方法对NAR模型参数及状态的估计更加精确,对股票价格走势的预测更加准确。
4 结束语
粒子滤波方法是一种非线性滤波方法,能很好地解决非线性问题,但是在对非线性自回归模型进行状态估计的过程中容易出现粒子退化现象,所以本文提出了一种基于辅助粒子滤波与灰色预测相结合的NAR模型状态估计算法。通过加入辅助变量,进行两次加权操作,降低了对外界干扰的敏感度,灰色预测理论对重采样后的粒子状态进行了修正,有效地克服了粒子退化现象。结果表明,基于辅助粒子滤波与灰色预测相结合的方法优于传统的NAR和粒子滤波估计方法,更适合于金融时间序列的预测和分析。
