企业物流成本对企业效益影响的多元线性回归分析

袁水林

（山西财经大学 会计学院，太原 030012）

0 引言

中国的物流业发展与发达国家相比，还处于初级阶段，在发展的过程中存在诸多问题，其中最主要的就是过高的物流成本。企业物流成本的高低关乎企业效益，目前我国企业物流成本主要存在管理不完善、运输及存储成本过高、信息管理技术落后等问题。企业财会部门并没有专门设立物流项目，对于物流各环节的成本无法进行合理规划与控制。由于我国物流发展起步较晚且不够成熟，从而其设备以及仓储水平均低于全球平均水平，同时我国大部分企业的物流过程很多都难以实现机械化，无形之中增加了物流成本。我国企业对于物流信息管理目前很难实现及时追踪、沟通以及处理，这也增加了我国企业的物流成本，从而在短时间内很难提高企业效益。同时，物流成本具有隐含性、效益背反以及物流成本削减的乘法效应等特点，这也增加了研究企业物流成本对企业效益影响的难度。

纵观国内外学者对企业物流成本的研究，大都集中于理论方面[1-8]，而数据类的实证研究内容较少。因此，本文以某公司为例对两者进行实证分析，根据多元线性回归模型分析了企业物流成本对经济效益的影响，并根据研究结果对企业未来的经济效益进行了估计,寻找出合理的物流成本管理法，以促进企业经济效益的增加。

1 研究设计

1.1 多元线性回归法

在市场经济活动中，当几个因素对某一经济现象具有决定作用，且这几个影响因素之间无法分析其主次时，就可以构建多元线性回归方程，构建模型的依据是各影响因素之间的关系，根据各变量之间的相关性确定最主要的影响因素。在本文的实证分析当中，某商贸有限责任公司的年销售额受到各个物流成本之间的影响，根据此相关关系建立多元线性回归模型，并对其进行分析[9]。假设x1，x2，…，xm表示自变量，且自变量受因变量Y的因素影响，表达公式为：

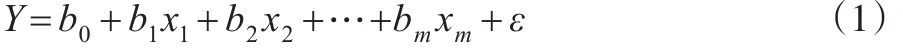
式（1）中，ε为零均值的随机变量；x1，x2，…，xm为可以控制的变量；b0，b1，b2,…，bm为未知参数；也可以将式（1）称为多元线性回归模型，并且m＞1。

通过对可控变量x1，x2，…，xm的n次观察，可以得出n组观察的值为 xi1，xi2，…，xim，yi，其中i取值为1，2，…，n。可以表示为：

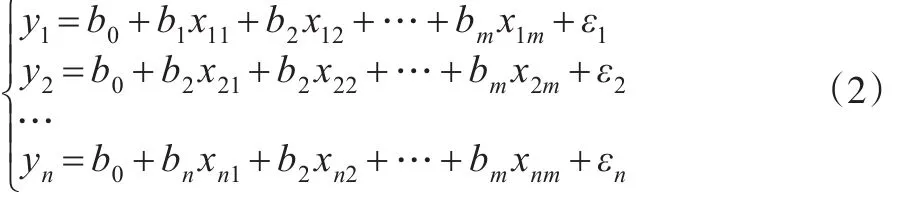
计算未知参数b0，b1，b2,…，bm，可以通过最小二乘法求得，并将计算结果代入式（1）中：

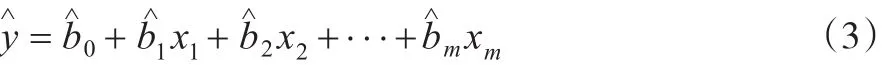
1.2 模型假设与检验基础

1.2.1 模型假设

在物流成本体系当中，可能会有许多个自变量和因变量y之间存在相关性，对变量y和x1、x2、Λ、xp间的定量联系进行研究[10]，此过程就为多元线性回归分析。其表达公式为：

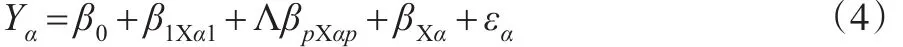
式（4）中，εα是各自独立的，α=1，2，Λ，n。使用最小二乘法对参数β进行计算，从而得出多元线性回归方程：

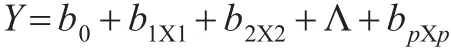
对线性回归模型进行设定，满足以下几个条件，可以将其称为传统线性模型：

（1）正态性的假设，∈i为随机误差项，且其服从平均值为零，满足方差是σ2的正态分布；

（2）等方差的假设，σ2为全部xi和∈i的条件方差，同时σ的取值范围是常数，公式表达为

（3）独立性假设也可称之为零均值假设，对xi进行规定的前提下，∈i的条件期望值是0，那么E( )∈i=0；

（4）没有自相关关系，∈i为随机误差项，其逐观测值之间互补，也就是

（5）∈和自变量x间不存在相关性，∈i和xi均对因变量y产生影响，这就证明了这两个变量对因变量y的影响是可以区分的，

综合上述五种假设，传统线性模型的使用条件比较严格。首先，其所选取的样本数据需满足对应分布特征，分布特征有正态分布和对数正态分布两种；其次是解释变量与那些无相关、独立的变量间能够构建良好的函数关系。

1.2.2 检验基础

构建完成的多元线性回归模型需要对其进行检验，三种常见检验方法为：

（1）判定系数检验，又可称为R检验。多元线性回归模型的判定系数检验和一元线性回归相似。用R来表示判定系数，其公式为R=R，当R值接近1时，代表Y和X1，X2，...，Xk间的线性关系紧密；当R值接近0时，就说明Y和X1，X2，...，Xk间的线性关系不紧密。

（2）回归系数显著性检验，又可称为t检验。在多元回归分析当中，对模型当中各自变量和因变量间有无明显的线性关系进行检验，这种检验称为回归系数显著性检验。其显著性可以由各个回归系数的t检验值计算得出，公式为为回归系数bj的标准差。

在多元线性回归模型中，当一个变量的回归系数未通过t检验，这就说明自变量与因变量之间的线性关系不够显著，因此在对其进行回归分析时，可将此自变量剔除，也可以根据实际情况作出适当的调整[11]。

回归方程的显著性检验，又可称为F检验。其检验方法是将全部自变量当做整体，看其和因变量间有无明显的线性关系。其显著性由F检验可得，公式为：F=(m，n其中为回归平方 和 ，m 为 自由度 ；为剩余平方和，（n-m-1）为自由度。在对自变量进行选取时，可能忽略了重要的因素或者自变量和因变量间的非线性关系，而导致回归方程无法通过F检验，这就需要重新建立模型。

2 实证分析

2.1 数据来源

本文数据来源于某商贸有限责任公司在2007—2016年的经营原始数据（见表1），通过查阅相关资料整理得出，运用SPSS软件对选取指标进行多元线性回归分析。

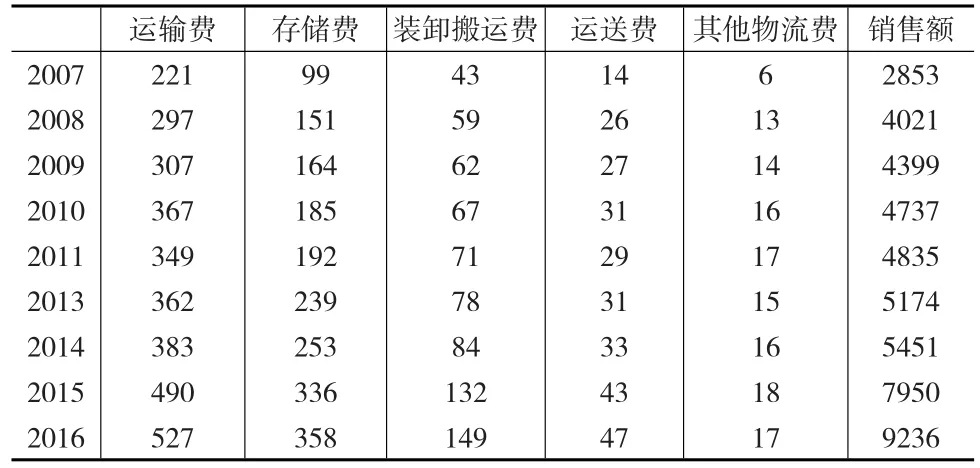
表1 某商贸公司经营原始数据汇总表 （单位：万元）

2.2 变量说明

因该公司在经营过程中，各流通加工以及包装费用的相关数据并不是很全面，同时该商贸公司极少涉及到流通运输和包装相关业务，因此在对原始数据进行整理时就将这两项合为一体总称为其他物流费。自变量参数的选择是：X1为运输费、X2为存储费、X3为装卸搬运费、X4为运送费、X5为其他物流费，因变量参数Y为企业的年销售额，采用SPSS对这些相关数据进行多元线性回归分析。

2.3 模型构建

多元线性回归模型是指线性回归模型中含有两个或者两个以上的自变量。一般情况下，对多元线性回归模型的假设是：设Y为因变量，且因变量所表达的是m个自变量X1,X2，…,Xm的函数，有n组实际观测数据。

设因变量和自变量之间存在线性关系，其函数表达式为：

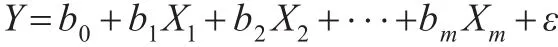
也可以将上式表达为：

其中，Xij为可观察的一般变量；yi为可观察的随机变量，并且其随着Xij的变化而变化，同时受实验误差的影响；εj为独立并且都服从N（0，σ2）的随机变量，也就是，对于b1,b1,b2,…,bm和方差σ2的计算，要从实际观察值来进行估测。

2.4 回归结果分析

采用SPSS软件对上述相关数据进行分析，得到的分析结果如下页表2所示。

根据分析结果可以得知其回归方程式：

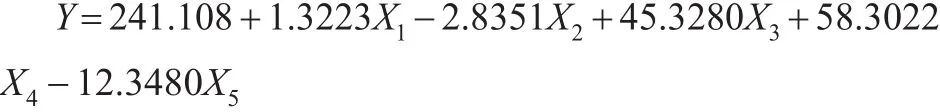
从上述构建的模型中可以得出，该商贸有限责任公司的年销售额估计值和实际销售额非常接近，如下页表3所示。

使用上文中提到的三种检验方法对构建的模型进行检验，其检验结果如下:

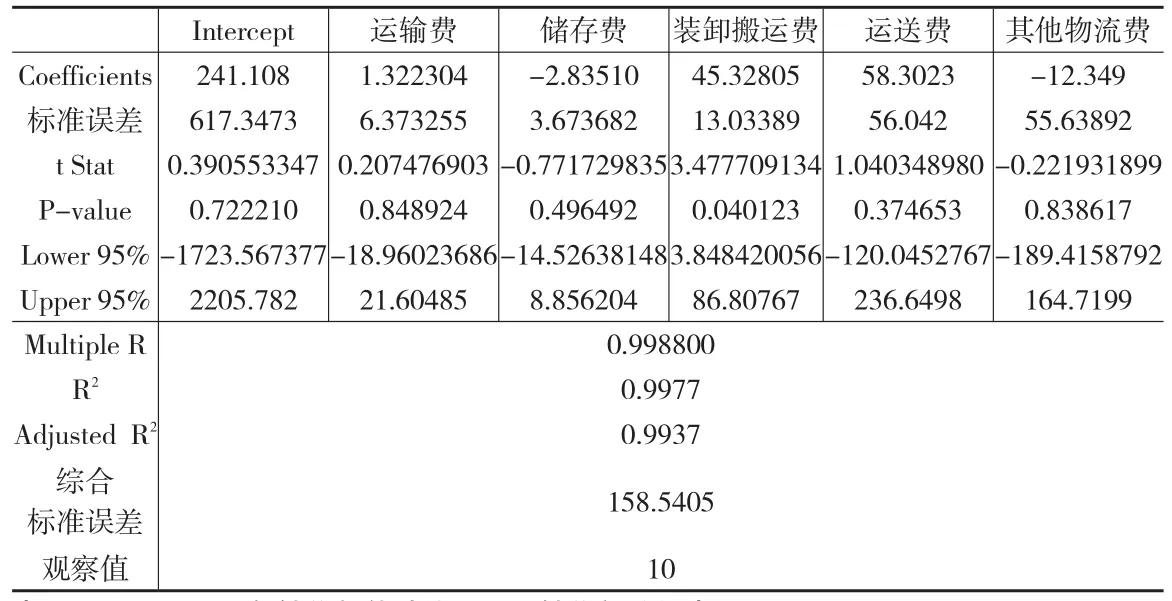
表2 模型回归结果

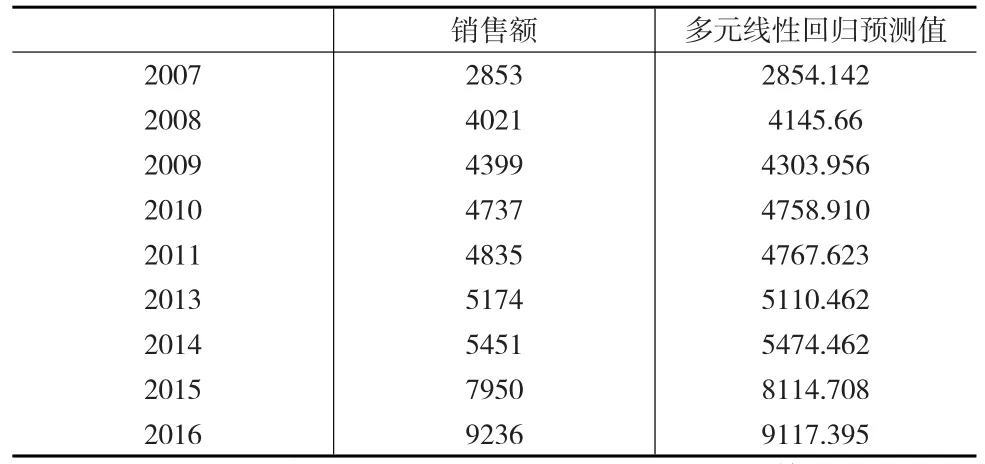
表3 年销售额估计值和实际销售额分析表

（1）定系数检验法（R检验）：R=0.9988，R值接近1，这证明相关关系紧密，也说明模型构建的拟合度很好。

（2）回归方程的显著性检验（F检验）：F=249.4125，查看F分布表可得，α=0.06，F0.06（5,3）=5.42，F=249.4125＞Fα=5.42，这就证明符合线性的假设，其有很明显的回归成果。

（3）回归系数显著性检验（t检验）：如果进行t检验，就需要大量的相关数据，本文所采用的数据不够充足，所以不做此检验，并不会对本文的最终结果产生较大影响。

根据上述的分析结果来看，X1（运输费）、X2（存储费）、X3（装卸搬运费）、X4（运送费）、X5（其他物流费）的相关系数分别是1.332、-2.8351、45.3281、58.3023、-12.349，从上述数据中可以得知公司的年销售额和运输费、装卸搬运费、运送费之间成正比，和存储费、其他物流费成反比。这里所讲的正反比关系并不是数学领域上的，也就是说并不是公司的运输费、装卸搬运费、运送费越高，就代表公司的销售额越好；也不是储存费及其他物流费越低，公司销售额就好；运输费、装卸搬运费、运送费的提高，就代表物流成本费用的增加，这会逐步侵占公司的利润；存储费及其他物流费的减少，也不能表示企业利润的增加，这是由于在企业物流流通过程中，流通加工与包装能够给企业带来附加值。

本文中所讲的正反比关系是指，企业贸易量即企业每年商品销售量的增加，也会相应地增加运输费、装卸搬运费以及运送费，从而导致销售额的增加，这种现象主要是企业规模扩大造成的；企业年销售额和储存费及其他物流费呈反比是指在确定一定销售规模下，企业对储存费及其他物流费进行合理控制，使企业成本降低，并且提高企业经济效益。

3 结论与建议

本文对某商贸企业经营数据构建多元线性回归模型并进行实证分析，得出阻碍企业物流发展重要因素是其管理水平较低，但这也是国内企业物流发展现状。面对这一问题，并结合多元线性回归模型分析的结论，就如何降低企业物流成本从而提高企业效益给出如下建议：

第一，对企业物流成本加强管理控制。加强企业物流成本的管理控制，需要企业从根本上改变企业理念与管理机制，对各方面因素进行综合考虑，制定出可以实施的策略，能够在一定程度上达到物流成本的降低[12]。

第二，企业物流进行第三方外包服务。企业若将物流业务外包给第三方物流，就能节省在物力、财力、人力上的投资，同时专业的第三方物流能够提供更专业的物流运输、存储等业务，为企业及客户提供更好的服务，也能使企业更加注重其核心业务。

第三，完善物流信息体系的构建。物流运输过程中，管理销售订单、商品的跟踪处理系统、货物运输系统等都是其不可或缺的服务体系，但是将这些系统完整地整合在一起，目前的管理体系尚不能做到[13]。因此，就我国目前企业状况来讲，企业将相关物流业务与第三方物流相互合作，能够更好地建立物流信息管理体系，以及将各个供应商与顾客之间联系起来，打造一个完善的物流服务体系。