运用变式教学 提升学习效率

徐忠

摘要：目前在初中数学教学中存在教育观念落实、教学方法较为陈旧、学生的课业负担重等问题，为了新课改的需要，数学教学一定要转变思路，创新教学方法，以提升学生的数学案养，而变式教学的运用为这一切的实现提供了可能。

关键词：变式教学;初中数学;教学效率

目前变式教学已经逐渐得到了人们的认可，尤其在初中数学教学中，得到了普遍的运用，但是在变式教学中还存在一些问题，这就要求老师在教学中要转变教学观念，创新教学理念，突破传统的教学模式，以变式教学来提升学生的数学思维能力，提高初中数学课堂教学效率。

一、重视概念的变式教学

目前在初中数学教学中普遍存在的问题是学生解题思路狭窄，数学思维僵化，不能建构完整的知识系统，导致学生的学习效率低下。如何改变这一现状是每位教学者值得思考的问题，而变式教学的运用，为解决这一弊端提供了可能。

1.运用变式突出概念的本质属性

目前初中数学中关于概念的引导主要采用两种方式，一是通过直观观察获取认知;二是采用变式教学形成抽象概念，体现概念的本质属性。很明显第二方式有利于学生数学思维的提升和能力的提高。

比如在学习“旋转”的概念时，针对一个图形的旋转时，支点不同、角度不同，得到的图形变式就不一样，但是旋转的本质没有改变，通过变式可以掌握旋转的本质属性，使学生的数学能力得到提升。

如图1，等边三角形ABC内有一点O：

如果将三角形AOB旋转到三角形ADC，那么会出现DC=OB、AD=AO，又因為角DAO=60°，就能够得出等边三角形中OD=OA，那么三个线段再经过旋转就会组成一个新的三角形，经过这样的变式之后，就会获取新解题思路。

2.运用变式拓展概念的外延

数学概念之间不是单独存在的，它往往会形成一个概念的体系，每一个概念都会存在于这一体系中，而且又会形成自己独立、清晰的概念边界，这就要求在概念辨析时能够区别其属性。

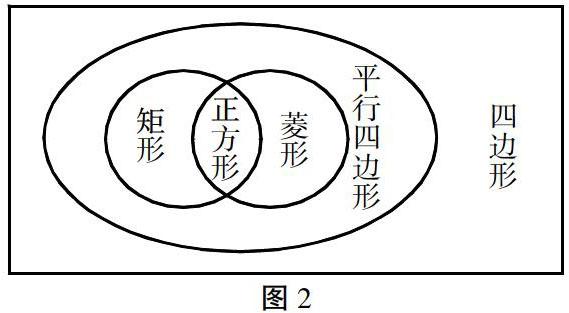
例如图2中就表示出正方形概念与其他概念之间的交叉关系，因此在学习正方形的概念时要注意仔细的区分。

二、重视运用过程性变式，提升学生解题能力

在教学中老师可以通过问题解决式的过程性变式，促使学生建立起问题之间的有效联系，由已知问题推导未知问题，让复杂问题简单化，通过这种变式教学好似给学生的解题搭建了一个脚手架，帮助他们剖析问题，理顺解题思路，提升解决问题的能力，通过这种变式教学，让学生理解了问题的生成过程。

例如有两车，其中一慢一快，快车在慢车的前面，慢车车身长为125米，行驶速度为每秒15米。而快车车身长度为146米，它的行驶速度比慢车每秒多5米，那么，快车从赶上慢车到超过慢车共用了多长时间？

这时可采用如下的变式进行解答：

变式一：小华家在铁路旁边，一天当他看到一列车以25米每秒的速度从眼前经过，列车的总长为145米，那么，列车经过他的身边共花了多少时间？

变式二：小华在铁路旁边锻炼的速度是每秒3米，从他身后驶过一列车，其速度是25米每秒，列车总长为145米，那么列车经过小华身边共用了多少时间？

变式三：有一列车总长为150米，当它以每秒25米的速度经过一长度为600米的隧道时，共需要多长时间？

如图3：在这个关于超车的问题中，经过了三个变式，形成了递进式，帮助学生建构了解题的思路，将复杂的长问题分解为简单的短问题，让学生对整个的解题思路有一个清晰的认识，提升了他们的解题能力。

三、重视变式引导，做好自主创设

老师在教学中一定要做好变式引导，创设有针对性的情境，激发他们的自主思考意识，促进他们的思维活动，逐步弄清问题条件，形成知识间的融合贯通。

在具体的数学问题中，教师可给学生一个全开放式的变式，创设一种问题情境，让学生发挥想象设计题目，这样他们设计的这些问题可构成一个变式系统，在这个系统中的问题都是符合生活且有意义的，然后让学生之间进行互问、互答，以检测问题的真实性，在这种交流的过程中提高了他们的解题能力，促进了数学思维的发展。

总之，在初中数字教学中，变式教学是一种行之有效的教学方式，它可以促进学生学习习惯的养成，能够提升学生数学思维能力。

参考文献：

[1]聂必凯.数学变式教学的探索性研究[D].华东师范大学，2004.

[2]顾泠沅，杨玉东.过程性变式与数学课例研究[J].上海中学数学，2007（Z1）：98.

编辑 鲁翠红