不同形状扰流柱对溢流层板腔内流动与换热特性的影响

高 宇，谭晓茗，单 勇

（南京航空航天大学能源与动力学院航空发动机热环境与热结构工业和信息化部重点实验室，南京 210016）

层板冷却结构集合多种冷却技术于一身，具有冷气使用量少、冷却效率高等优点［1］，成为航空发动机热端部件冷却设计关注的焦点。针对这一冷却结构形式，国内外展开了一系列研究工作。Jeng等［2］利用实验研究了不同排列方式下方形扰流柱的流阻和换热特性，并与圆形扰流柱做了比较，归纳出了压损与热传递之间的关系。Sweeney等［3-4］利用红外摄像仪测量温度的方法对层板冷却有效性进行了实验研究。赵乃芬［5］确定了层板的冷却结构形式，并对其进行了数值计算和实验研究，分析了结构参数对流场特性、换热特性的影响规律。孙启超［6］通过数值模拟和实验的方法，分析不同形状的扰流柱、孔柱之间的排列方式、扰流柱直径、射流雷诺数等参数对层板冷却结构内部流动与换热特性的影响规律。谭晓茗等［7-8］对7种不同的层板结构进行了流动与换热的耦合计算，分析了排布方式、堵塞比等参数对层板冷却效率与相对压损的影响规律，对涡轮叶片尾缘通道中不同形状的扰流柱作用下的流动换热特性进行了实验研究，研究结果表明：圆形和哑铃形的扰流柱换热情况较好而水滴形扰流柱作用下的压损最低。胡娅萍等［9］基于相似理论方法对简化层板的腔内流动与换热特性进行了实验研究，分析了扰流柱为菱形和没有扰流柱时2种实验模型的阻力系数、靶板面的温度和对流换热系数分布。卢元丽等［10］对简化的层板冷却叶片前缘进行了数值模拟研究，比较了冲击双层壁和带有3种不同形状（圆形、方形、菱形）扰流柱的层板冷却叶片前缘的流动与换热情况。王鸣［11］针对2种孔柱排布方式、2种冲击孔轴线与靶面的夹角设置方式对叶片前缘换热的影响进行了数值模拟研究。研究结果表明：冲击孔径越小及数目越多，靶面的换热系数就越高；冲击孔轴线和靶面的夹角对流阻和叶片前缘的换热影响不大。何跃龙等［12］对几种不同形状扰流柱的层板冷却结构的内部进行了流阻实验及数值模拟，发现了层板冷却结构的内部流场极其复杂。Han等［13］研究了3种不同填充比的层板结构，发现适当增大填充比可以提高层板的冷却效果。Funazaki等［14-15］对不同冲击孔直径、气膜孔直径、堵塞比和不同通道高度的层板进行了数值模拟和换热优化分析。Favaretto等［16］对不同结构参数的层板进行了数值模拟和换热优化分析。

上述的研究取得了许多有价值的成果，然而层板冷却结构相对比较复杂，其冷却性能受到很多因素的影响，因此对该技术还需要进行更加系统、详细和深入的研究。本文主要研究在溢流条件下不同形状扰流柱以及射流雷诺数对层板腔内流动与换热特性的影响规律。

1 物理模型和计算方法

1.1 物理模型

考虑到实际多孔层板结构的周期性，本文采用了一个层板单元作为计算模型，其结构如图1和图2所示。层板模型由冲击板、溢流孔板和夹在中间的扰流柱组成，冷气由冲击孔流入由溢流孔流出，冲击板和溢流孔板的尺寸为20 mm×20 mm，高度都为3 mm。扰流柱高度为6 mm。层板单元包括1个冲击孔、4个1／4溢流孔和4个扰流柱（1∶1∶4），冲击孔直径、溢流孔的直径都是4 mm，扰流柱直径为3 mm，其他形状扰流柱占据通道的体积分数保证与圆形扰流柱一样。层板计算模型包括固体域和流体域，冲击板、溢流孔板以及扰流柱为固体域，其余为流体域。

图 1 孔柱排布示意图（1∶1∶4）

图2 层板计算模型

1.2 边界条件

考虑到层板内部流动的对称性，所有侧面均定义为对称性边界条件。冲击孔进口为流量进口，不同的进口流量对应的 Rej＝（2 000～10 000），冷气温度为300 K；溢流孔出口采用压力出口，出口压力为101 325 Pa；溢流孔板面为加热面，热流密度为50 kW／m2；其余壁面采用无滑移壁面边界条件。

1.3 网格划分

利用Gambit软件对计算模型进行网格划分，图3为孔柱附近的网格划分，冲击孔和溢流孔内壁、扰流柱外壁划分了附面层网格。由于壁面附近流动非常复杂，因此对壁面附近进行了加密处理。为了验证网格独立性，本文计算了5套网格，网格数目分别为 150、180、210、250、280万。当计算网格为250万左右时，冲击板表面、溢流孔板表面和扰流柱面的对流换热系数不再随网格的增加而变化，所以不同扰流柱形状对应的层板模型计算网格数控制在250万左右。

图3 孔柱附近网格划分

1.4 湍流模型验证

为了使数值计算的结果更加精确可靠，在数值计算之前验证和选择合适的湍流模型是非常有必要的。本文在湍流模型验证中选择文献［14］里的实验结果作为标准。图4是文献［14］里面的实验值和不同湍流模型计算值之间的比较，对比Target Plate（靶面）、Pin（扰流柱面）、Overall（靶面和扰流柱面）的平均Nu，其中SST k-ε湍流模型的数值计算结果与实验值差距最小，所以在本文中选择SST k-ε湍流模型对层板模型进行数值模拟研究。压力场求解采用SIMPLEC算法进行压力-速度耦合求解，离散方程均采用二阶迎风差分格式进行计算，收敛精度为10-5，残差趋势趋于平直且冲击板面、溢流孔板面和扰流柱面的温度变化不大。

图4 不同湍流模型计算值与实验［14］比较

1.5 参数定义

1.5.1 雷诺数的定义

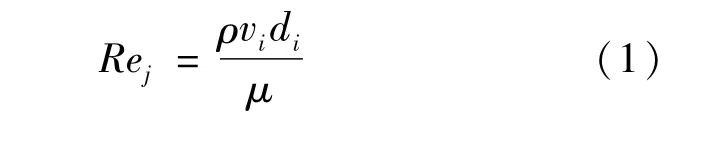
式中：ρ、vi分别表示冲击孔进口的密度和速度；di表示冲击孔直径；μ表示动力黏度。

1.5.2 对流换热系数的定义

式中：qw表示壁面的热流密度；Tw表示壁面温度；Tc表示冲击孔进口冷气温度。

1.5.3 努塞尔数的定义

式中λ表示冷气导热系数。

1.5.4 总压损失系数的定义

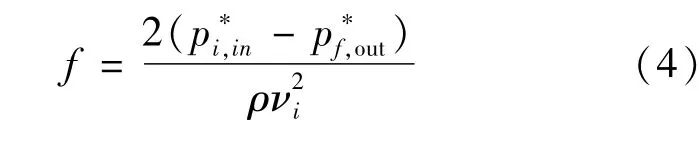
为了衡量层板结构冷却效果的好坏，这里引入一个表征换热性能强弱的K值，K值的定义为

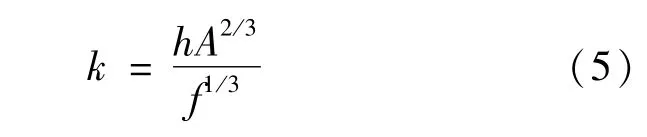
式中A表示湿润面积。

2 计算结果与分析

2.1 扰流柱面换热分析

图5是不同形状扰流柱面的换热系数分布，由图可知：扰流柱底部换热系数的值很高，菱形和椭圆形扰流柱底部换热系数最大，而正方形扰流柱高换热系数区域分布最广，射流沿着正方形扰流柱柱高方向爬升的高度最高，这是因为正方形扰流柱的正对迎风面积比其他几种扰流柱的都大。图6是B-B截面（截面位置如图1）的流线和量纲为一速度云图，很好地揭示了以上现象：射流冲击到溢流孔板上，流向由冲击孔轴向转为径向形成壁面射流直接冲击扰流柱的根部，使得扰流柱迎风面根部换热系数很大，在射流的两侧形成2个方向相反的漩涡，沿着扰流柱柱高方向爬升，对冲击板形成二次冲击。而不同形状的扰流柱正对迎风面积不同，射流沿着扰流柱爬升的高度不同，高换热系数的区域也就不一样。

图5 不同形状扰流柱面换热系数分布

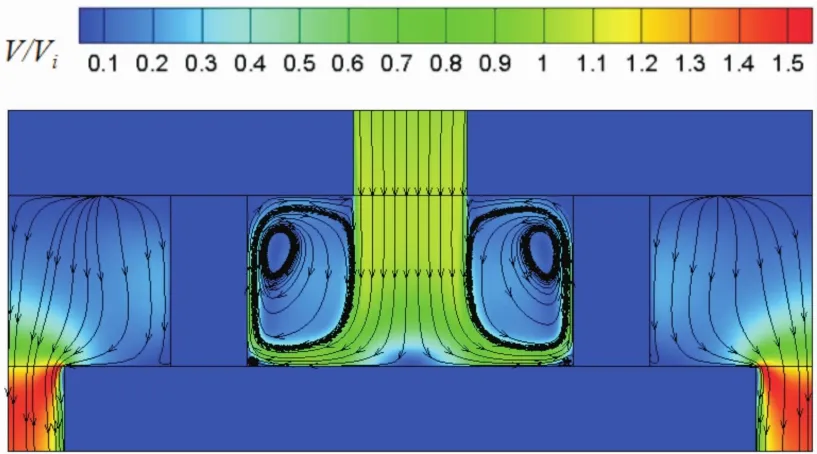
图6 B-B截面的流线和无量纲速度云图

2.2 冲击板和溢流孔板面换热分析

图7 给出了Rej＝10 000时溢流孔板面的换热系数分布云图。从图7可以看出：在驻点附近是高度紊流度区，使得换热得到加强，所以在冲击滞止区换热系数很大；随着离驻点距离慢慢变大，黏性附面层的厚度逐渐增厚，使得换热不断减弱，沿着冲击孔径向换热系数逐渐减小，且滞止区换热系数云图成“十”字形，菱形扰流柱对应的溢流孔板面换热云图“十”字形相对其他形状扰流柱对应的溢流孔板面换热云图旋转了45°。冲击孔之间的换热系数相对较低，在溢流孔周围由于溢流的抽吸作用，会使换热系数比周围有所上升，在扰流柱附近由于正方形扰流柱正对迎风面积最大，对气流的扰动作用最强，导致扰流柱后形成的回流漩涡最大，使得气流流过正方形扰流柱时最容易产生分离而使换热削弱，所以正方形扰流柱周围换热系数和其他几种扰流柱相比是最低的。而水滴形和椭圆形扰流柱的柱型型面更加贴近流线型，这2种扰流柱周围换热系数最高，圆形和菱形则次之。图8为A-A截面（截面位置如图1）的流线和量纲为一速度云图。由图8可知：冷气冲击到溢流孔板面之后滞止，使得溢流孔板面边界层遭到破坏而厚度变薄，从而驻点区换热系数很高，然后冷气由冲击孔的轴向转向径向形成壁面射流，随着射流远离滞止中心边界层逐渐发展使得换热系数逐渐降低。

图7 溢流孔板面换热系数云图

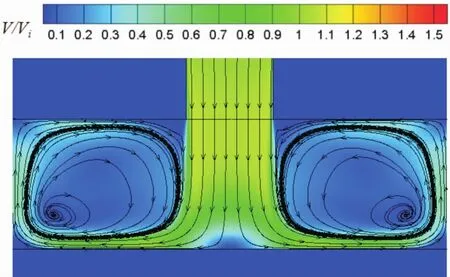
图8 A-A截面的流线和无量纲速度云图

图9 是不同形状扰流柱对应的冲击板面换热系数分布云图。从图9可以看出：2冲击孔之间的换热系数较大，而冲击孔和扰流柱之间的区域换热系数较小，对于正方形扰流柱对应的冲击板，在冷气由冲击孔的轴向转向径向形成壁面射流冲击到扰流柱面，气流就会沿着扰流柱高度方向爬升，由于正方形扰流柱正对迎风面积最大，气流爬升的高度最高，对冲击板面形成二次冲击，强化了冲击板面的换热，所以在正方形扰流柱前缘出现局部高换热区。从图9还可以看出：射流在溢流孔板面的强烈反卷和离开冲击孔后对其周围的流体产生诱导作用，在其两侧形成了2个大小几乎相同方向相反的漩涡。在2个冲击孔漩涡相撞处气板形成了小漩涡，使得溢流孔板面此处换热系数较低。2个漩涡相互作用后，对冲击板而言形成射流冲击，所以在2个冲击孔之间存在换热系数比较大的区域。

图9 不同形状扰流柱对应的冲击板面换热系数云图

2.3 扰流柱形状对溢流孔板面（加热面）温度分布的影响

图10 是不同形状扰流柱对应的溢流孔板面的温度分布云图。以菱形扰流柱对应的溢流孔板面（图10（a））为例，溢流孔板面的中心温度最低，这是由于该区对应冲击驻点区换热强烈，溢流孔孔周围由于溢流的抽吸作用增强了溢流孔内壁的换热，使得溢流孔周围温度也较低，而溢流孔板面的四周由于换热能力较其他地方低，所以温度最高。对比几种扰流柱形状下对溢流孔板面温度的影响发现，菱形扰流柱对应的溢流孔板面温度最低，椭圆形则次之，圆形最高，说明在加热量相同的情况下菱形扰流柱对应的层板结构换热效果最好。

图10 溢流孔板面温度分布云图

2.4 不同扰流柱形状下热量在溢流层板内的分布

图11 是从溢流孔板面（加热面）传递过来的热量在层板内的分布。各个面的导热比重是冷气通过层板各个换热面带走的热量与加热面传递给层板热量的百分比，而各个面的热量是由面上的平均热流与面积的乘积得到的。热量从加热面进入溢流孔板，其中大部分从溢流孔板进入到腔内的冷气，一部分通过溢流孔壁进入冷气，剩下的部分通过扰流柱进入腔内，热量在腔内大部分被冷气带走，其余小部分热量通过扰流柱和冷气传递到冲击板，在冲击板内热量通过冲击孔内壁面被冷气带走。由以下各图可知，随着Rej的增加，不管是何种扰流柱，冲击板面和冲击孔壁面导出的热量所占的比重一直减小。溢流孔板面和溢流孔壁面导出的热量在总热量中所占的比重一直增加，但是溢流孔板面增加得更快。而扰流柱的导热比重随Rej的增加，不同扰流柱形状会略有不同，对于菱形、椭圆形、正方形扰流柱面的导热比重随Rej的增加而无明显变化，而水滴形和圆形扰流柱面的导热比重随Rej的增加而降低。在Rej比较低时，冲击孔壁的导热比重比溢流孔壁大，而随着Rej的增加，在溢流孔内冷气速度随之增加，换热能力大大加强，所以导热比重超过了冲击孔壁。在所有的雷诺数下，从加热面进入层板的热量大部分是在冷气通过层板腔内带走的，因为腔内的冲击冷却使溢流孔板面有很高的换热系数、扰流柱的扰动强化了换热以及腔内有丰富的换热面积。

2.5 不同扰流柱形状对腔内换热性能的影响

图12是层板模型腔内K值随Rej的变化。由图可以看出，针对冲击板面（图12（a））而言，冲击板面的Ki值随Rej的增大而增大，且各种形状扰流柱对应的冲击板面的Ki值随Rej的增大差值越来越大，扰流柱为菱形对应的冲击板面Ki值最大，扰流柱为椭圆形对应的冲击板面Ki值最小，当Rej＝10 000时，扰流柱为菱形对应的冲击板面Ki值比扰流柱为椭圆形对应的冲击板面Ki值增加了44.1%。对于溢流孔板（图12（b）），水滴形对应的溢流孔板面Kf值最大，正方形对应溢流孔板面 Kf值最小，Rej＝10 000前者比后者高出6.4%，其他3种扰流柱对应的溢流孔板面Kf值区别不是很明显。对于扰流柱面（图12（c）），当Rej≦4 000时，各扰流柱面之间的Kp值随Rej的变化不是很敏感，当Rej≧4 000时，圆形扰流柱面和水滴形扰流柱面的Kp值远小于其他3种形状扰流柱面的Kp值，其中正方形扰流柱面的Kp值最大而圆形扰流柱面的Kp值最小，Rej＝10 000前者比后者高出30.3%。下面分析一下腔内的Kt随 Rej的变化（图 12（d）），Kt随 Rej的增大而增大，两者几乎呈线性关系，随Rej的增大各种形状扰流柱对应的腔内的Kt的差值增大。扰流柱形状为菱形时对应的腔内Kt的值最大，扰流柱形状为水滴形时对应的腔内Kt的值最小，Rej＝10 000前者比后者高出8.7%，而对于扰流柱形状为菱形时对应的腔内Kt的值在Rej＝10 000时比Rej＝2 000时高出8.5倍，综上可以得出，扰流柱形状为菱形对应的层板换热效果最好。

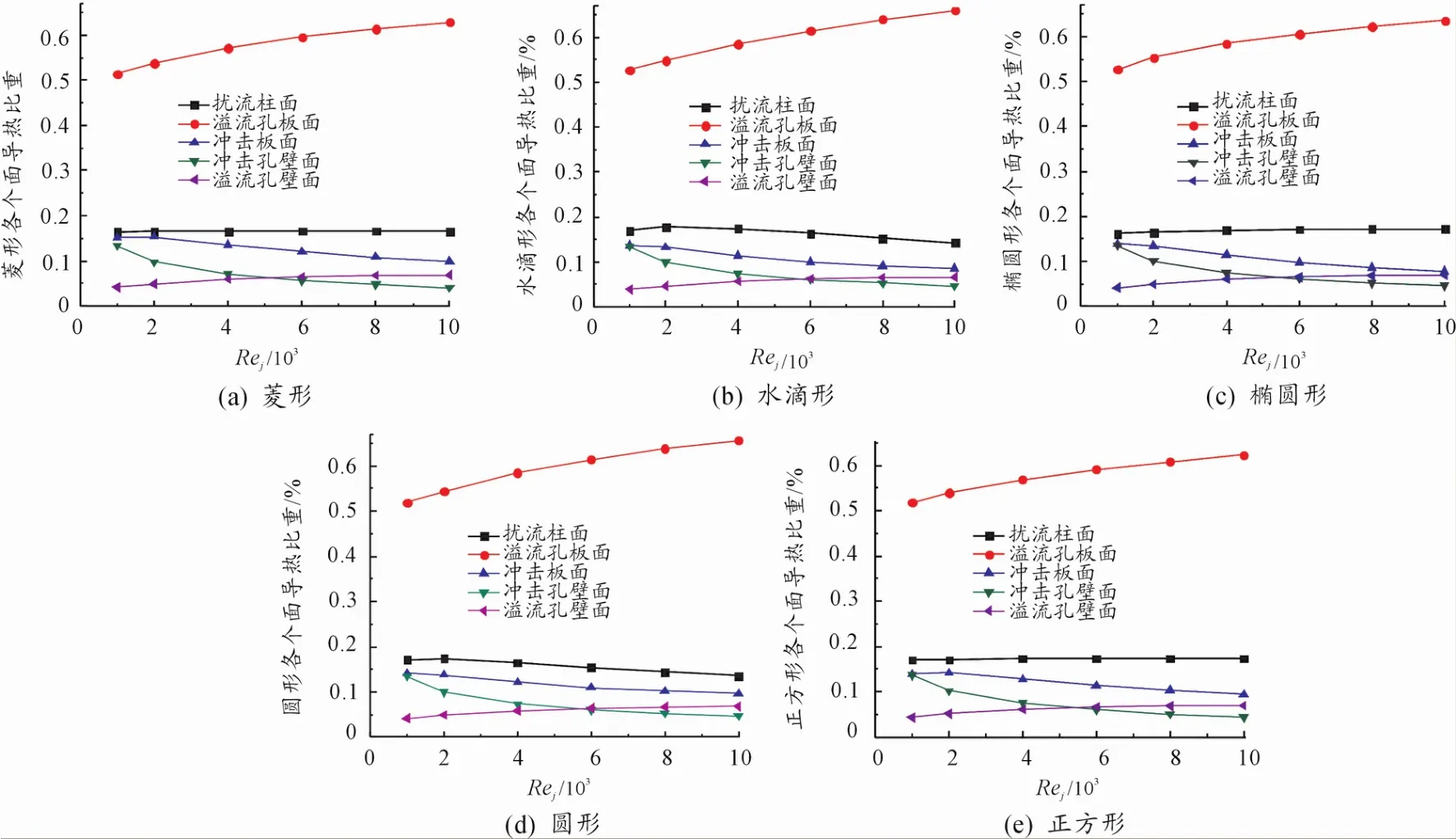
图11 层板模型5处壁面热量传递随Rej的变化

图12 层板模型各壁面和腔内K值随Rej的变化

3 结论

1）在不同扰流柱形状对应的层板结构中，水滴形扰流柱对应的溢流孔板面平均对流换热系数最高，正方形扰流柱对应的溢流孔板面平均换热系数最低；菱形扰流柱对应的冲击板面平均换热系数最高，椭圆形扰流柱对应的冲击板面平均换热系数最低；正方形扰流柱面的平均换热系数最高，圆形扰流柱面的平均换热系数最低。

2）在不同形状扰流柱对应的层板结构中，菱形扰流柱对应的加热面温度最低，圆形扰流柱对应的加热面温度最高。

3）在加热面进入层板内的热量大部分是在冷气通过层板腔内时带走的，当Rej＝10 000时，最高可占到总热量的89.3%，而且冷气通过层板腔内带走的热量随Rej的增大而增加。

4）在几种形状对应的层板结构中，菱形扰流柱对应的层板结构腔内的Kt值最大，换热效果最好，不管是什么形状扰流柱对应的层板结构腔内的K值随Rej的增大几乎呈线性增加。