基于装配机械弹性车轮的车辆平顺性的油气悬架优化研究

赵又群，叶 超，白毅强

（南京航空航天大学，南京 210016）

为使车辆适应恶劣的行驶环境，其平顺性及操纵稳定性的改善具有十分重要的意义。本课题组研究的一种机械弹性车轮，由于拥有较大的侧偏刚度，能增强车辆在复杂路面下的操纵稳定性［1］，但由于其大径向刚度特性导致了平顺性的不足［2-3］。为保证该种车轮的实际应用效果，需要进行悬架优化。而油气悬架的非线性刚度与阻尼特性能较好地改善车辆的平顺性，被广泛地用于越野车、高级轿车以及工程、军事车辆中［4］。二者的结合对提升车辆性能意义重大。

油气悬架的各项参数对其性能有着复杂的影响，传统优化算法难以胜任。随着优化算法的发展，群智能优化算法由于能处理多变量多目标的优化问题逐渐在工程优化上得到普及。目前国内外相关学者对于油气悬架的非线性特性［5］、结构设计［6-7］以及半主动控制［8-9］等方面研究已经做了大量工作，但对于油气悬架的设计参数优化的相关资料较少［10-12］。对于多目标、多参数的油气悬架优化算法的选取以及针对不同车辆参数及环境的优化效果仍需要进一步的研究。

本文以某越野车为例，建立了包含机械弹性车轮与油气悬架的半车模型，在此基础上，以提升平顺性为优化目标确定优化参数，利用量子遗传算法对油气悬架参数进行了多目标、多参数的优化设计，并对优化结果进行了分析。

1 机械弹性车轮

本文所采用的机械弹性车轮结构如图1所示。该车轮主要由轮毂、车轮外圈及连接二者的12个铰链组组成。经仿真分析与实车实验研究后，得知其拥有的大侧偏刚度保证了车辆的操纵稳定性，但是其相对于子午线车轮较大的径向刚度会对车辆的平顺性产生不利影响［2］。

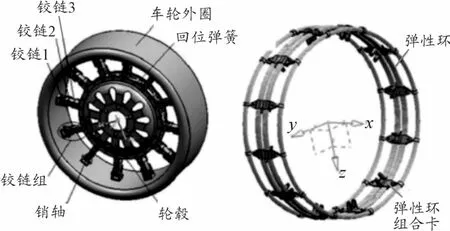
图1 机械弹性车轮结构示意图

已有的研究中，课题组使用轮胎特性静载试验台对车轮的径向刚度进行了测量，并在Adams中建立了车轮的有限元模型对其径向刚度进行仿真，得到车轮的静载径向刚度为630 390 N／m，其值约为普通子午线轮胎的2倍［13］。为简化问题，不失一般性，本文取该刚度进行研究。

2 车辆平顺性仿真模型

2.1 单筒式油气弹簧

油气弹簧是在膜式空气弹簧的基础上发展而来的，是油气悬架的核心部件。本文所研究的一种单筒式油气弹簧的结构示意图如图2所示［14］，它将气室置于活塞杆内部，使得结构更加紧凑。其工作原理是通过气室内的惰性气体的压缩与膨胀缓和冲击，通过活塞与油腔内的油液流动衰减振动。

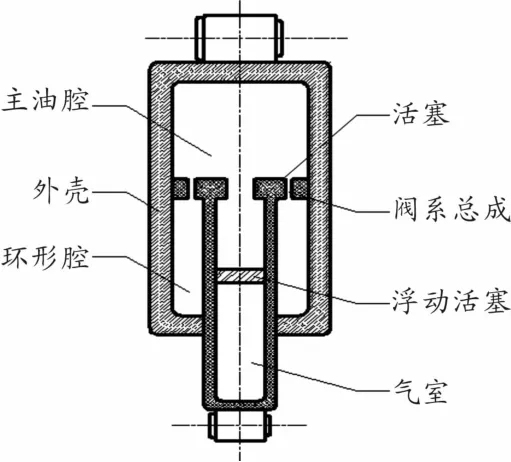
图2 油气弹簧结构示意图

油气弹簧的弹性力主要由气室内的惰性气体的状态变化来提供，一般使用氮气。依据理想气体状态方程可以得到，当活塞位移为x时，此时的弹性力为：

式中：p为活塞位移x时气室内的压强；Ag为活塞杆内腔截面积；ms为前悬架或后悬架的静载质量；V0为初始充气体积；n为气体多变指数，油气弹簧运动速度较快，气室内气体可近似视为绝热状态，这里取n＝1.4。

油气弹簧的阻尼力主要由油液通过阻尼孔与单向阀在主油腔与环形腔之间流动来提供，单向阀仅在压缩行程时打开。由小孔节流公式可以得到，当活塞速度为v时，此时的阻尼力为：

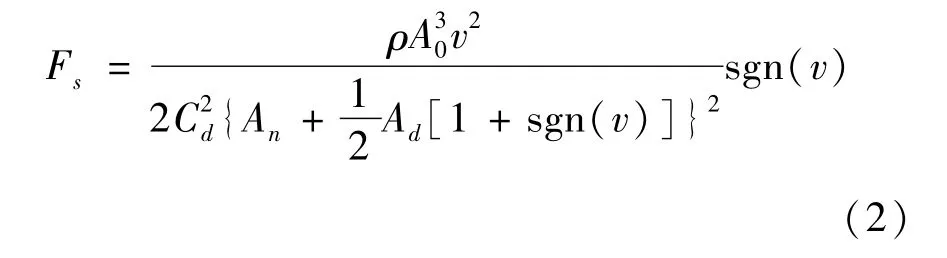
式中：Cd为小孔节流的流量系数，这里取 Cd＝0.68；ρ为油液密度；A0为环形腔横截面积；An为等效阻尼孔面积；Ad为等效单向阀横截面积。本文研究的油气弹簧的初始参数如表1所示。

在Matlab／Simulink中建立该油气弹簧的模型，得到的油气悬架弹性力-位移曲线与阻尼力-速度曲线如图3、4所示。该结果符合油气悬架的非线性特性［5，11-12］，模型较好地完成了油气悬架性能的模拟。

2.2 4自由度半车模型

为提高优化计算的效率，同时考虑车辆前后悬架的差异，本文通过建立一种4自由度半车模型对油气悬架进行平顺性优化［15］，其示意图如图5所示。

表1 油气弹簧参数

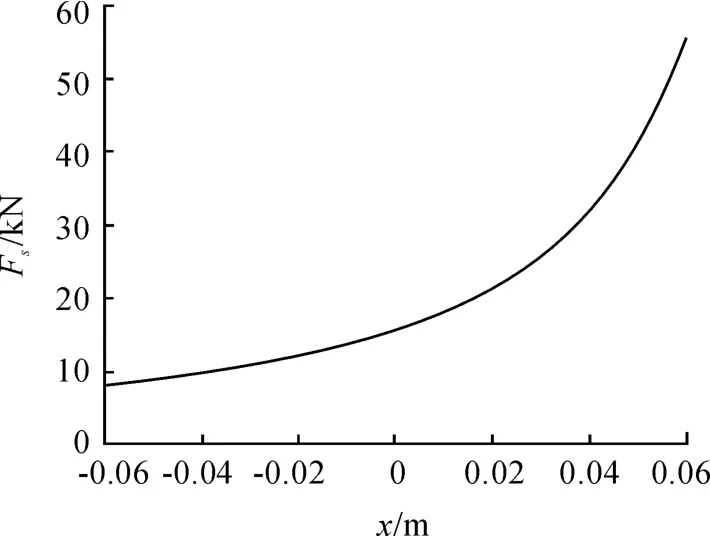
图3 油气悬架弹性力-位移曲线

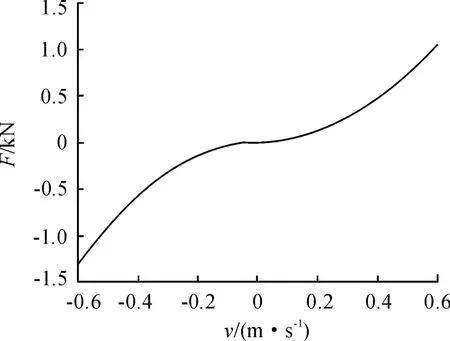
图4 油气悬架阻尼力-速度曲线

图5 中：ms为簧载质量；Jφ为绕y轴的转动惯量；φ为绕y轴的转动角度；xc为质心竖直位移；L为轴距；b为前轴距；xs1、xs2分别为前后轴竖直位移；ks1、ks2分别为前后悬架刚度；cs1、cs2分别为前后悬架阻尼；mt1、mt2分别为前后簧下质量；xk1、xk2分别为前后簧下质量的竖直位移；kt1、kt2分别为前后车轮刚度；xr1、xr2分别为前后路面激励。

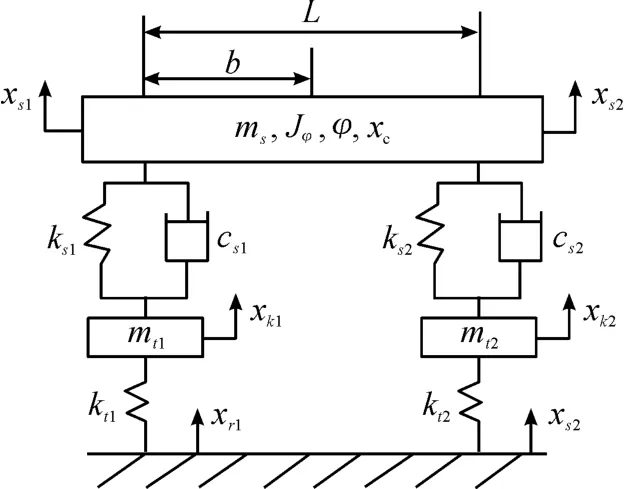
图5 4自由度半车模型

建立半车模型时使用的越野车参数如表2所示。

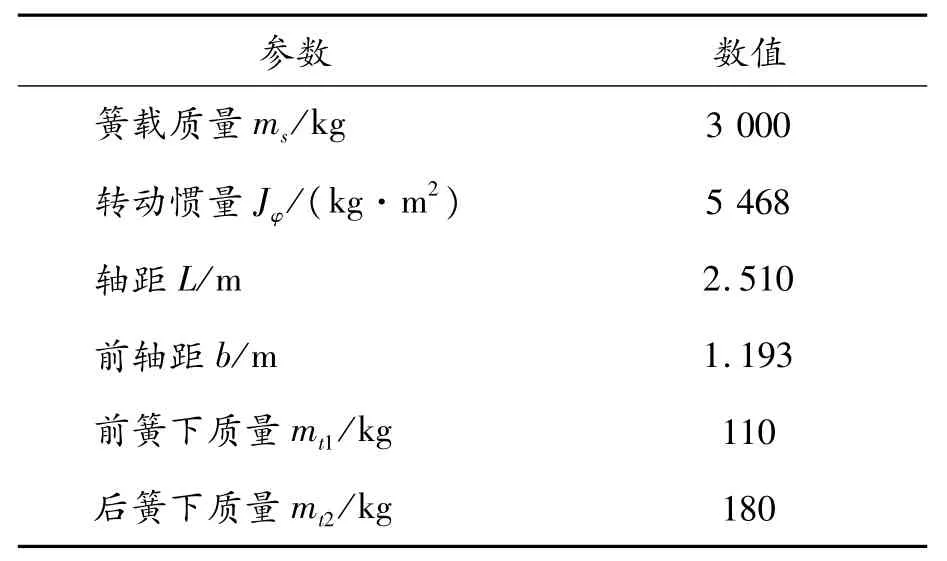
表2 越野车参数

2.3 路面白噪声输入

现阶段主要采用路面的功率谱密度来描述研究车辆振动时路面不平度的统计特性［16］，路面的功率谱密度表达式为

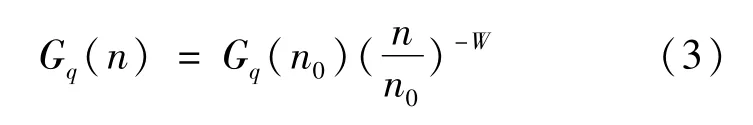
式中：n为空间频率；n0为参考空间频率，n0＝0.1；W为频率指数；Gq（n0）为参考空间频率下的路面不平度系数。本文在优化时以C级路面为研究对象，取 Gq（n0）＝256×10-6，车速设定为20 m／s。

2.4 车辆装配机械弹性车轮与普通子午线轮胎的平顺性对比

为验证机械弹性车轮是否对车辆平顺性造成负面影响，分别使用机械弹性车轮与普通子午线轮胎在不同等级路面下进行仿真实验，这里采用的子午线轮胎径向刚度为 320 450 N／m［13］，平顺性指标为垂向振动与俯仰振动的加权加速度均方根值，实验结果如表3所示。

表3 机械弹性车轮与普通子午线轮胎在不同环境下的平顺性指标

我国规定［16］，在评价车辆平顺性时要考虑椅面x、y、z 3个方向（纵向、侧向、垂向）的振动。这里做出如下假设：

1）假设座椅在车辆质心位置，且与车辆间没有减震系统。

2）车辆加权加速度均方根值是3个方向的均方根值的加权和。由于车辆在x轴与y轴方向的振动加权加速度均方根在不平路面直线行驶时远小于z轴方向，故忽略x轴与y轴方向的影响。

由实验结果可知，在C级及以下等级路面上，普通子午线轮胎车辆的垂向加权加速度均方根值均小于 1，人的主观感觉为“有一点不舒适”（0.315～0.63）到“不舒适”（0.5～1）之间。由于假设1忽略了座椅的减震性能，故实际给人的主观感觉会更好，符合平顺性的要求。在相同的车型、悬架的初始参数以及路面条件与车速下，装配机械弹性车轮车辆的平顺性要差于装配子午线轮胎车辆，而油气弹簧参数的可设计性使得该问题有望得到改善。

3 油气悬架设计参数优化

3.1 量子遗传算法

遗传算法（genetic algorithm，GA）具有极高的鲁棒性，被广泛应用于各个领域的研究。但GA容易出现迭代次数多，或陷入局部极值等问题。因此研究者们对GA进行了一系列的改进［17-18］。

量子遗传算法（quantum genetic algorithm，QGA）是一种将量子计算机与GA结合的概率进化算法。QGA将量子的态矢量表达引入遗传编码，利用量子逻辑门实现染色体的演化，由于采用量子比特编码的染色体可以表达多个态的叠加，相较于常规GA具有更高的多样性，不易陷入局部极值，且能更加逼近全局极值。QGA于1994年由Chor首先提出［19］，是一种新型智能优化算法，并在应用过程中不断得到改进［20］，其已被用于信号处理、智能控制、TSP问题等领域，而工程设计方面的使用目前较少。

3.2 目标函数

质心的加权加速度均方根值是最常用的评价车辆平顺性的指标，根据GB 7031—1987［21］规定，当振动的波形峰值系数小于9时，加权加速度均方根值的计算公式为

式中：Wk（f）为垂向振动频率加权函数；Ga（f）为质心垂向振动加速度的功率谱密度。由此得到目标函数：

考虑车身的俯仰运动带来的平顺性问题，以俯仰角振动加权加速度均方根值来表示：

式中：We（f）为俯仰振动频率加权函数；Gβ（f）为俯仰角振动加速度的功率谱密度。由此得到目标函数：

考虑到不平路面行驶过程中车轮与地面脱离的情况，需要对车轮的接地性进行优化。车轮的动载荷系数是常见的评价车轮接地性的指标，其物理意义为车轮动载荷均方根值与静载荷之比，计算公式为：

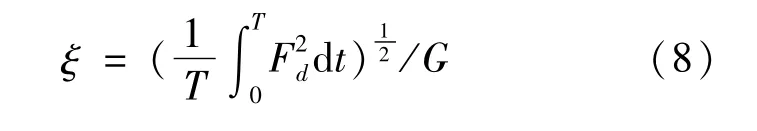
式中：Fd为车轮动载荷；G为车轮静载荷。由此得到目标函数：

式中ξf、ξr分别为前后车轮动载荷系数。

目标函数J1、J2、J3、J4都要求尽可能小。

3.3 设计变量

影响油气悬架性能的参数多且复杂，需兼顾优化效率与实际优化效果进行选取［22］。考虑到实际生产加工的统一，取活塞杆内腔面积Ag以及环形腔面积A0不变，并通过控制变量法研究其他参数对油气弹簧性能的影响。图6～8分别反映了初始充气体积V0、等效阻尼孔面积An与等效单向阀面积Ad对油气弹簧刚度与阻尼特性的影响。

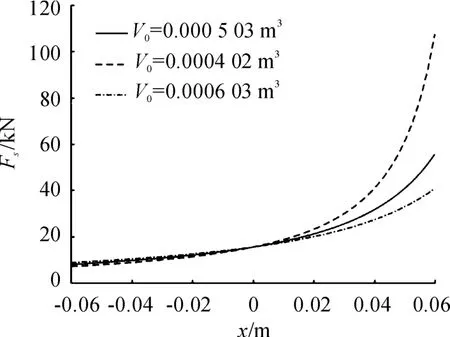
图6 初始充气体积对刚度的影响

图7 阻尼孔面积对阻尼的影响

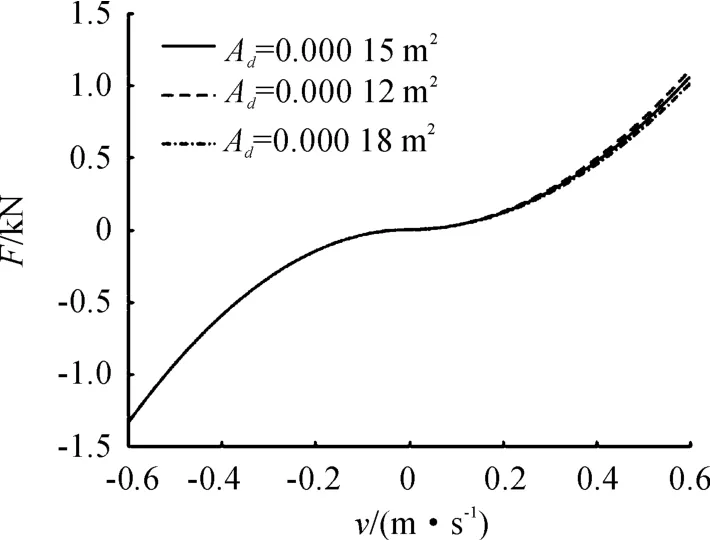
图8 单向阀面积对阻尼的影响

通过仿真结果结合公式易看出，单向阀面积对阻尼特性的影响较小。考虑到油气弹簧的单向阀结构相对复杂，为方便生产，前后弹簧采用相同尺寸的单向阀。综上，可以确定设计变量分别为统一的等效单向阀面积、前后弹簧初始充气体积、前后等效弹簧阻尼孔面积。

3.4 约束条件

3.4.1 边界条件约束

边界条件用于规定个体基因表达的范围。

设计单向阀时需要考虑它与活塞的的相互布置位置。同时，由于是内置式气室，故初始充气体积应小于活塞杆内腔体积。由于使用了小孔节流公式，故等效阻尼孔面积的选取不能太大。

3.4.2 中间变量约束

中间变量以罚函数的形式在算法中表现约束力。

依据加速度均方根值与人的主观感觉评定表，将加权加速度均方根值最大值awmax设定为1.25 m／s2。且一般认为，当车轮的动载荷系数低于1／3时，车轮跳离地面的概率在0.15%以下。当悬架的动行程S的均方根值低于悬架最大动行程Smax的1／3时，限位块撞击概率在0.3%以下。

3.5 数学模型

由此得到的油气悬架优化的数学模型为：

使用表1所提供的初始参数进行计算［11］，得到的4个优化目标的初始值如表4所示。由初始结果可知，质心垂向加速度均方根值为1.055 0，此时人的主观感觉为“相当不舒适”。为保证车辆平顺性，需要对油气悬架进行优化。

表4 各优化目标初始值

经过综合分析，将4个优化目标的权重分别定义为：0.4、0.3、0.15、0.15。考虑到优化方便程度，可将4个优化目标加权相加得到一个整体优化目标，即：

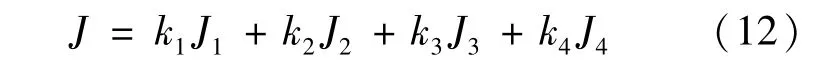
式中ki为第i个优化目标相对应的加权系数，这里采用初始值作为参考，其值按照式（13）计算。

3.6 优化参数选取

本文经过多次尝试后确定的优化参数如表5所示。

表5 参数选取

4 优化结果分析

4.1 优化对比

为保证量子遗传算法结果的可靠性，使用相同的初始参数进行了3次优化运算，优化结果如表6所示。

由表6可知，量子遗传算法多次优化结果之间的差异性在1%左右，说明该算法较为稳定。选取其中综合优化效果最好的第1次优化结果进行研究，其优化过程如图9所示。由图9可知：优化目标绝对值在刚开始计算的时候迅速下降，在100代左右达到最优值附近，并在之后趋于稳定。

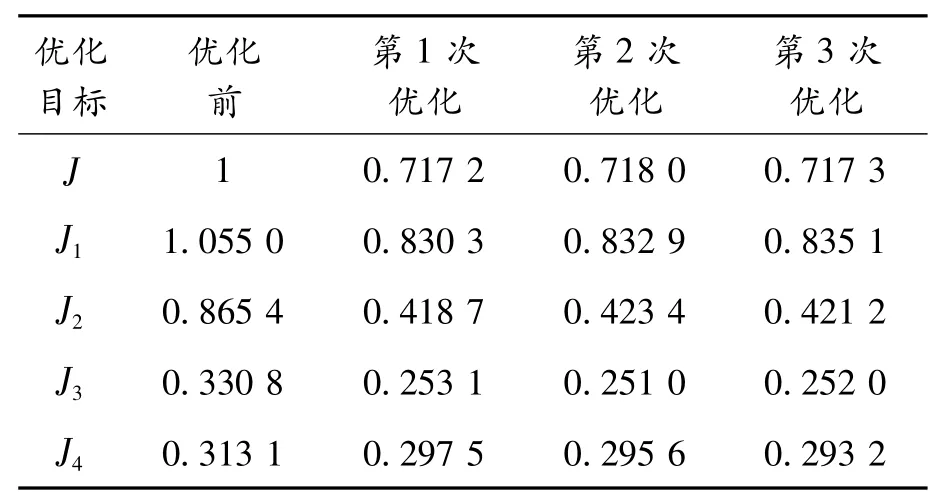
表6 量子遗传算法结果对比

图9 量子遗传算法进化过程

4.2 优化结果

由表6可知，第1次优化后，总的优化目标、垂向振动加权加速度均方根值、俯仰振动加权加速度均方根值、前后车轮动载荷分别改善了29.3%、21.3%、51.1%、23.5%、4.98%，越野车的平顺性得到了较大幅度的提升。

优化前后的各参数参数如表7所示。

表7 优化前后油气悬架各参数值

将表中数据代入模型中进行计算，得到优化前后质心垂向振动加速度、俯仰振动加速度、车轮载荷对比，如图10～13所示。从图中也可以看出，优化后车辆的平顺性得到了改善。

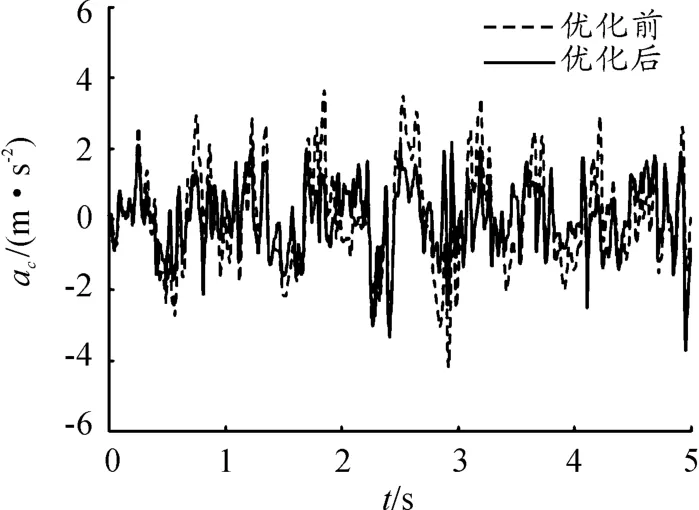
图10 优化前后垂向振动加速度

图11 优化前后俯仰振动加速度

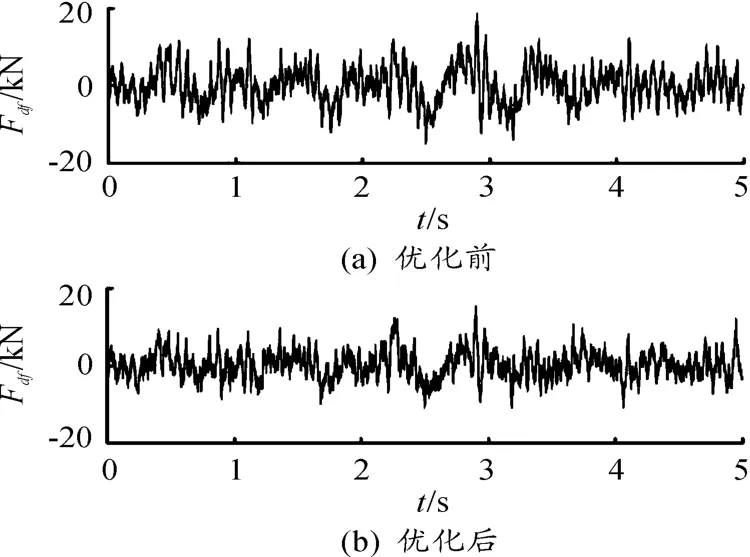
图12 优化前后前轮载荷

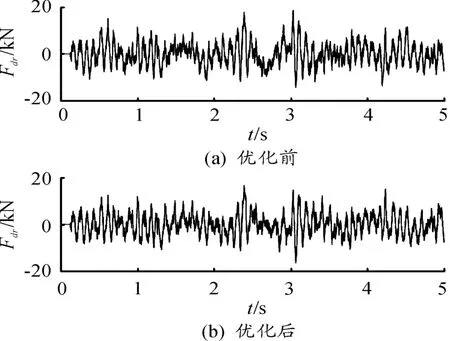
图13 优化前后后轮载荷

4.3 优化效果验证

优化时使用的路面条件为C级路面，车速为20 m／s。油气悬架优化后，在不同的路面条件及车速下进行效果验证，取平顺性的重要评价指标，即垂向振动及俯仰振动的加权加速度均方根值来进行效果比较。验证结果如表8所示。

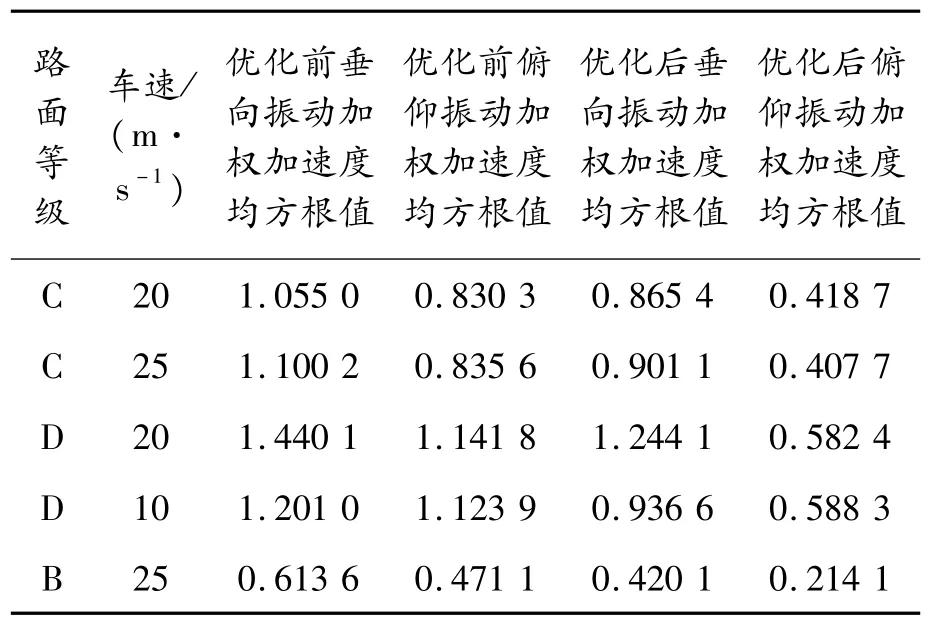
表8 优化前后不同环境下的平顺性指标

由表8可知：不管在怎样的路面条件及车速下，优化后的平顺性都要优于优化前。优化后俯仰振动均有大幅度改善。除在D级路面25 m／s的车速下之外，其他条件下都将垂向振动加权加速度均方根值降至1以下，达到了使用优化前油气悬架的子午线轮胎车辆的平顺性水平，人的主观感受为“有一点不舒适”（0.315～0.63）到“不舒适”（0.5～1）之间。由于忽略了座椅的减震性能，故实际给人的主观感觉会更好，符合平顺性的要求。而对于D级以上路面，则可通过适当降低车速来保证平顺性。

5 结束语

机械弹性车轮的大径向刚度特性会导致车辆平顺性的降低。通过建立车辆平顺性仿真模型，对在C级路面白噪声输入下以20 m／s车速行驶的装配机械弹性车轮的越野车进行平顺性优化，结果表明：各平顺性评价指标皆得到了改善，优化后符合平顺性要求。可见量子遗传算法用于油气悬架的多目标优化设计较好地完成了任务，具有一定的可行性。

本文仅考虑了半车的平顺性，以后的工作可以综合考虑整车、座椅及其他工况下的性能。本文采用的优化算法不失一般性，可以使用本文所阐述的方法同时通过改变各参数、优化目标、边界条件等适用于不同行驶环境、车型以及设计目标，为油气悬架的优化设计提供一种简易可靠的方法。