基于整车卡尔曼观测器的主动悬架控制研究

2019-02-22季云华汪若尘丁仁凯孟祥鹏

重庆理工大学学报(自然科学) 2019年1期

季云华，汪若尘，丁仁凯，孟祥鹏

（江苏大学汽车与交通工程学院，江苏镇江 212013）

传统被动悬架由于其阻尼刚度不可调，只能在特定路况下处于最佳工作状态［1］，而主动悬架能根据不同的路况进行主动控制，从而在很大程度上提高动力学性能［2］。常见的主动控制方法有天棚控制［3］、LQG控制［4］、PID控制［5］、神经网络控制［6］等。其中天棚控制较为简单且能最大限度地提升车辆的舒适性，但会增大轮胎动载荷，影响车辆的操纵稳定性。改进天棚控制是在天棚控制的基础上加入被动阻尼以减小天棚控制对轮胎动载荷的恶化［7］。

（2）施工必须权责分明，使施工人员明确自己的职责，施工出现渗漏问题，往往都是施工不当所引起的所以，在施工中如果工程质量出现了问题，要立刻能够找出责任人，对其进行责任追究，这样可以最大程度的减少施工质量问题的出现。

改进天棚控制需要依据精确的簧上质量绝对速度以及悬架相对速度信号来进行控制［8］。现有传感器很难对线速度进行采集，且通过对加速度积分以获得速度会导致最终误差过大。为了获得精确的速度信号，需要建立状态观测器对改进天棚所需的速度信号进行估计。卡尔曼滤波算法通常被用来对线性定常系统的状态变量进行估计，如文献［9-11］对悬架状态进行估计。但这些研究仅针对1／4悬架进行估计，且建立的悬架模型为连续系统，而在实际应用中传感器采集的是离散信号，并且现在还没有相关研究针对的是改进天棚控制的整车状态估计。

本文针对以上问题，建立了整车七自由度模型，进一步将整车定常连续系统进行精确离散化，利用卡尔曼滤波算法设计了基于改进天棚控制的整车卡尔曼观测器。卡尔曼观测器可利用整车中7个加速度信号（质心垂直加速度、车身俯仰角加速度、车身侧倾角加速度以及各悬架簧下质量加速度）估计出各悬架顶端簧上质量的绝对速度信号以及各悬架的相对速度信号，并将这些速度信号作为反馈输入至改进天棚控制算法中，从而对整车悬架进行控制。

1 整车动力学模型

1.1 整车模型

图1为包括质心垂向、俯仰、侧倾运动以及4个车轮垂向运动的七自由度整车模型。

进一步推导出整车各自由度的运动微分方程：

四十多岁，就疾病缠身，这种遭遇，大抵是悲催的。以至于我长时间处在一种忧虑与焦躁的状态当中。戒酒是必须的。有几次，在泸州和毕节，都是产好酒的地方，却不敢再喝一口。因此，我特别怀念自己还可以喝酒时候的某种癫狂状态。其实，酒解决和带入的是人生的混沌境界，这种混沌是激越和亢奋的，也是欢乐与丰富的，就像去掉了肉身，进入到了纯粹的灵魂仙境一般。

根据文献［12］建立左右轮距特性下的前轴双轮路面输入模型，仿真得到前轴两侧轮胎所受到的路面激励，见图2。

图1 整车动力学模型

1.2 悬架模型

理想天棚控制是在簧上质量上增加一天棚阻尼Csky与虚拟的固定物相连，阻尼器产生的阻尼力能抑制簧上质量的运动，因此能提高车身的舒适性，不过这部分阻尼力会加剧轮胎的运动，使得轮胎动载荷加大。改进天棚控制是在理想天棚控制的基础上增加1个被动阻尼Cs，能减小理想天棚控制对轮胎动载荷的影响。

各悬架改进天棚控制输出的控制力分别为：

朗读是用清晰、响亮的声音把文章读出来，以传达文章思想内容的活动。教学实践表明，大多数不会朗读课文的学生都缺少对语文学习的兴趣。

加上弹簧力之后，整车各悬架力分别为：

式中：Ksj（j＝F，R）表示前／后悬弹簧刚度。

由平均受教育年限的四分位图可见，中国各省的教育水平在空间区域的分布上存在着一定的共性，即可能存在空间相关性，为进一步分析教育程度的空间相关性，以基于数据的全局Moran指数I和局部空间Moran指数LISA来测度空间观测单元的整体及局部聚集程度。

式中：Csj（j＝F，R）表示前／后悬被动阻尼系数；Cskyj（j＝F，R）表示前／后悬天棚阻尼系数。

1.3 路面模型

左前轮胎所受的路面激励的微分方程分别为：

式中：f0为下截至空间频率，f0＝0.011 m-1；v为车速，v＝20 m／s；n0为参考空间频率，n0＝0.1 m-1；G0为路面不平度系数，在C级路面上行驶时G0＝256×10-6m3。

式中：Ms为簧上质量总重；Muj（j＝F，R）表示为前／后悬簧下质量；Iθ、Iφ分别为俯仰转动惯量、侧倾转动惯量；Kt为轮胎刚度；a／b、c／d分别为前／后轴至车身质心距离、1／2前／后轮轮距；Zs、θ、φ分别为簧上质量质心位移、俯仰角、侧倾角；Zs-ij（ij＝LF，RF，LR，RR）为各悬架顶部位移；Zu-ij（ij＝LF，RF，LR，RR）为各轮胎位移；Zr-ij（ij＝LF，RF，LR，RR）为各轮胎受到的路面激励；Fij（ij＝LF，RF，LR，RR）为悬架与车身连接点的悬架力。

图2 路面激励

当车辆沿直线匀速行驶时，后轴轮胎与前轴轮胎受到的路面激励存在固定时差，其值为（a＋b）／v。

2 整车卡尔曼观测器

层次加权分析法缺点有，评价的主观臆断性及其过程的随机性，从而使得结果的可信度降低。此外，当判断因素较多时，常常会因为层次分解和赋值的不一致而出现判断矩阵不一致的现象。

2.1 系统状态方程

在实验中，由于线速度较难测得，为了提高控制精度，可依据卡尔曼滤波原理，通过可精确测得的加速度信号将速度信号估计出。为了构建卡尔曼观测器，结合式（1）～（5），构建车辆状态方程：

2.2 连续系统离散化

由于式（6）为线性定常连续系统，而实际传感器采样的是离散型信号，因此需要将状态空间模型进行离散化。通常连续系统的状态方程的求解方程为：

由于W（τ）为路面白噪声，其均值为0，假设在同一采样周期内其值不变则可推出：

这个案例说明，把注意力投入在一件喜爱的事情上，是有疗愈功效的。它能让原本趋于混乱的精神能量变得有秩序，让人重拾生活的热情和意义。

式中：X（k｜k-1）是利用上一状态预测的结果；X（k-1｜k-1）是上一状态最优结果。之后进行协方差更新：

现在只考虑在采样时刻t＝kT和t＝（k＋1）T时刻之间的状态响应，即对式（7）取 t0＝kT，t＝（k＋1）T，可得：

进一步分析可知式（6）离散化成立的条件为：Φ（T）＝exp（AT）。由于离散化的对象为动态的状态方程，而式（6）中输出状态方程为静态的代数方程，其离散化之后保持不变，令 G＝（At）d t）B1，H＝C，最后得到离散化之后的系统状态方程为：

2.3 卡尔曼滤波算法

式（11）的输出的状态参数为加速度信号，实际传感器测得的加速度信号都带有测量噪音，因此为了使模型更接近实际，需对式（11）中输出状态加入测量噪声V（k）。路面输入的白噪声W（k）以及测量噪声V（k）的均值都为0、方差阵分别为Q与R，且W（k）与V（k）不相关。最终，得到卡尔曼滤波器的状态方程与观测方程分别为：

由于加速度传感器测量精度高，在整车中可用来测量各位置的加速度信号。受技术限制，准确的速度信号一直较难获得，因此对天棚或改进天棚控制的实际实施带来困难。卡尔曼滤波可根据传感器获得的观测信号对相关状态变量进行估计或预测。为了获得精确的速度信号，本文利用卡尔曼滤波算法设计了改进天棚控制的整车状态观测器。

利用卡尔曼滤波算法进行状态估计时，需对现在状态进行预测。首先，进行过程更新：

三、没破坏仓库的任何一处，连窗户上的蛛丝也没碰一下，没留下任何脚印，连个鬼影子都没有，而仓库里的东西又明明丢了，进货我守着，出货我点着，到底是鬼还是神钻了空子？难道真如大家说的，这塔公村里居住更多的菩萨和鬼怪，真是菩萨和鬼怪沦到要干这下贱的活？哎！再怎么说，我都不会相信这世上真有什么鬼神，即使有，那也投胎在人心里。

从业近20年的殷红妹，为了让老百姓直观了解和掌握简易鉴别药品真伪的知识，她编制了宣传册，制作真伪中药实物和展柜，利用周末时间参与社会和大众组织的志愿者活动。

式中：P（k｜k-1）是 X（k｜k-1）对应的协方差；P（k-1｜k-1）是 X（k-1｜k-1）对应的协方差。之后计算卡尔曼增益：

进一步对状态进行更新：

最后计算k状态时的协方差：

3 仿真验证

为了验证基于卡尔曼滤波的改进天棚控制策略的性能，在Simlink中建立了的整车模型控制框架，见图3。整车模型将其质心加速度、俯仰角加速度、侧倾角加速度以及各簧下质量加速度输入至卡尔曼观测器中，卡尔曼观测器实时估计出各悬架顶端的绝度速度以及各悬架的相对速度。之后将卡尔曼观测器估计的速度信号输入至改进天棚控制算法中，经过计算，得出各悬架的控制力信号并输入至悬架系统中。最后悬架系统输出改进天棚控制力至整车模型中。通过对某车辆进行测量，得到车辆参数见表1。

在将卡尔曼观测器估计的速度信号输入至改进天棚控制算法之前，首先需要验证卡尔曼观测器的估计精度。为此在Simulink中将整车模型中的实际速度信号与卡尔曼观测器估计的速度信号进行对比，结果如图4～11所示。

中南佛州水利工程的设计与施工完全由联邦政府主导，到20世纪70年代基本竣工。从本质上讲，该项目有很大的应急成分，因此，在应用、管理过程中一些过去没有考虑到的问题逐渐显现。

由图4～11可看出：无论是各悬架顶端的绝对速度还是各悬架的相对速度，卡尔曼观测器的估计值与实际值相差都非常小，验证了所设计的整车卡尔曼观测器的估计精度非常理想。

与航磁异常类似，本区地面磁场总体上亦呈近EW向展布，其中测区南部和中北部宏观上表现为NWW—近EW向的带状低磁异常，而中东部呈NNE—近SN向相对高磁异常，反映二者所处地质背景不同，结合地球物理和区域地质特征，推测前者分别为高山、宝山岩体及其隐伏岩体引起，而后者主要为NNE向的构造所致。其中在图幅西南部的高山岩体及其隐伏地带磁场相对较平稳，说明该地带后期岩浆活动较少、岩体相对较单一；而在图幅东北部的宝山岩体及其隐伏地带磁场变化大、形态复杂，反映构造发育、岩浆作用频繁，成矿地质条件更为有利。此外，研究区中南部NWW—近EW向的条带状高磁异常带为高压输电线等人文干扰引起的假异常。

图3 控制框架

表1 整车系统参数

图4 左前悬绝对速度

图5 右前悬绝对速度

图6 左后悬绝对速度

图7 右后悬绝对速度

图8 左前悬相对速度

图9 右前悬相对速度

图10 左后悬相对速度

图11 右后悬相对速度

进一步将卡尔曼观测器所估计的速度信号代替模型中的实际速度信号，输入至改进天棚控制算法中，以验证基于卡尔曼观测器的改进天棚控制悬架性能。将传统被动悬架与无卡尔曼观测器的改进天棚控制悬架以及基于卡尔曼观测器的改进天棚控制悬架进行整车性能比较，仿真结果如表2和图12～16所示。

表2 仿真结果

结合表2与仿真图12至图16可知，与无卡尔曼滤波的改进天棚控制悬架相比，利用卡尔曼观测器估计出的速度信号进行改进天棚控制悬架的性能基本没有产生恶化，进一步验证了所设计的卡尔曼观测器状态估计的精确性。

图12 车身质心加速度

图13 俯仰角加速度

图14 侧倾角加速度

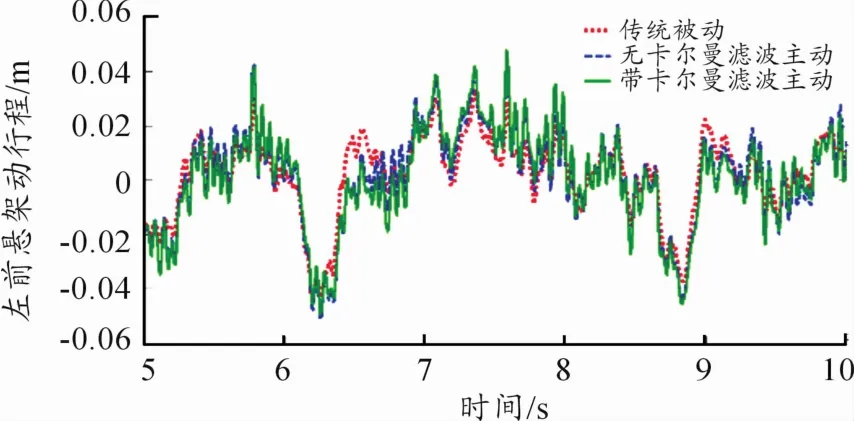
图15 左前悬架动行程

图16 左前轮胎动载荷

带卡尔曼滤波的改进天棚控制悬架较传统被动悬架，车身质心加速度降低了38.01%，俯仰角加速度降低31.11%，侧倾角加速度降低33.33%，从而表明带卡尔曼滤波的改进天棚控制悬架能够大幅度提高车辆的乘坐舒适性。与传统被动悬架相比，带卡尔曼滤波的改进天棚控制的悬架动行程恶化21.33%，但最大值依旧保存在6 cm以内，不会对悬架使用寿命产生影响。由于改进天棚控制中天棚控制阻尼会加剧轮胎的损耗，因此轮胎动挠度恶化31.20%。