质量静矩和惯性矩对水翼流致振动及噪声影响的数值研究

刘 龙， 张怀新， 姚慧岚

(上海交通大学 海洋工程国家重点实验室 高新船舶与深海开发装备协同创新中心，上海 200240)

在船舶行业中，有很多水翼[1-3]结构，像减摇鳍、舵、水翼艇的滑行水翼、潜艇的围壳舵和尾翼等都是典型的水翼结构。水翼结构在水中前行时会产生升力和力矩，如果设计得当可以用翼型的受力特点来改善船舶的水动力性能，应该注意到的是，翼型结构自身可以看成是一个弹性体，在流场力的作用下会产生振动和变形，当流体作用力较小或者说翼型结构强度较大时，这种振动会随时间趋于收敛，但是，当流场作用力达到一种临界状态时，翼型会产生发散或者颤振，发散是指速度大于一定值时，翼型的位移会不断增大，不围绕平衡点做往复振动的情况；颤振是指速度增大到一定值时，振幅不衰减，并有增大趋势。现在，船舶正向高速化发展，当翼型的内部结构(主要是质量静矩和质量惯性矩)设计不合理时，可能会影响水翼的性能和结构安全，另外，潜艇上翼型结构的振动产生的噪声也会威胁其隐身性能。因此，研究水翼的振动和噪声具有重要意义。

流致振动[4-7]是十分常见的问题，在翼型结构的流致振动问题的研究中，人们更多关注的是空气中机翼的流致振动，Theodorsen[8]提出的非定常气动理论可以快速求解颤振问题，从而它在机翼的气动力问题上得到了广泛应用，但是，由于它采用了简谐振动的假定，所以它不能求解发散问题。目前国内外对水翼的研究还比较少，水翼的研究主要集中在空泡[9-11]问题上。相对而言，弹性水翼流致振动问题的研究很少，试验研究主要集中在上个世纪。Woolston等[12]对NACA16-010翼型的稳定性做了试验，研究了相对质量比(质量比的平方根)和临界速度(刚好产生发散或颤振时的速度)的关系，结果表明，相对质量比小于3时，会产生发散；相对质量比大于3时，会发生颤振。Besch等[13]针对水翼，试验研究了NACA16-012翼型在四种不同质量比状态下的临界速度，结果表明，质量比为0.963的模型的颤振速度为24.7 kn，而另外三种质量比相对较小的模型没有发生颤振，只是出现了静态失效(静态发散)，静态失效速度为36 kn。Ducoin等[14]试验研究了NACA66312水翼由于边界层转捩而产生的振动。结果表明，边界层转捩会产生较大的振动，而振动的频率和幅度取决于涡脱落的频率。在数值研究上，刘晓宙等[15]进行了机翼的涡激振动和声辐射的研究，计算侧重于中、低雷诺数。计算结果表明，翼型在大攻角，当系统的频率恰当时，会出现共振；流体绕弹性翼引起的声辐射大于流体绕固定翼引起的声辐射，当弹性翼发生共振时，声辐射达到最大值。Chae等[16]根据Woolston等的试验数据，采用k-ωSST湍流模型数值计算了二维翼型NACA16-010的流致振动问题，数值计算结果和试验结果相吻合。Akcabay等[17]研究了两个自由度二维弹性水翼在空泡情况下的振动和受力特征。刘胡涛等[18]采用大涡模拟的方法数值计算了具有两个自由度的二维弹性水翼NACA0012的振动和声辐射问题，他在文章中指出，随着流速的增加，两个自由度振动的频率会趋于接近，最后会发生颤振，水翼振动主要影响低频噪声。对于水翼噪声问题，通常包括流噪声和流激噪声，流噪声由水翼壁面偶极子噪声和流场中的湍流噪声(四极子噪声)组成，在湍流不强烈的情况下通常不考虑四极子噪声。Kim等[19]采用NACA0018翼型计算了该翼型的涡脱落特性和噪声问题，计算结果表明，涡脱落频率可以在声压频谱图上捕捉到；偶极子噪声明显大于四极子噪声。

从前文的叙述可知，Theodorsen非定常理论在翼型颤振问题上运用广泛，它可以快速在频域里提供一个理论解，对水翼问题有一定的参考意义，但是它也有很多局限性，如不能求解发散问题和没有考虑黏性。基于Theodorsen 非定常理论的不足之处，本文将采用流固耦合的方法计算水翼的流致振动和声辐射问题，流场在Fluent里计算，运动方程在UDF(User Defined Function)里用四阶龙格库塔法求解，在每个时间步里，用UDF控制流场力和水翼位移的相互传递，在时域里模拟水翼的振动。另一方面，质量比会影响翼型振动的临界状态，而实际问题中，翼型的质量比往往是一定的，在这种情况下，要想提高翼型的临界速度就得从翼型的内部结构入手。翼型的内部结构关系到翼型的刚性位置和重心位置，更具体的说法是翼型的内部结构会影响翼型的质量静矩和惯性矩。由于以往研究者对水翼的质量静矩和惯性矩研究较少，所以，本文将采用NACA16-010翼型数值计算具有两个自由度的三维刚性水翼的流致振动和声辐射问题，重点研究质量静矩、质量惯性矩对水翼振动以及临界状态的影响，并分析不同振动情况下的声辐射问题。

1 数值计算

1.1 物理模型

本文将研究两自由度三维刚性水翼(只考虑结构运动，不考虑结构变形)在不可压缩流体中的流致振动问题，流体介质为水，三维水翼具有两个自由度，分别对应垂向运动和绕弹性轴的扭转运动。简化模型如图1所示。

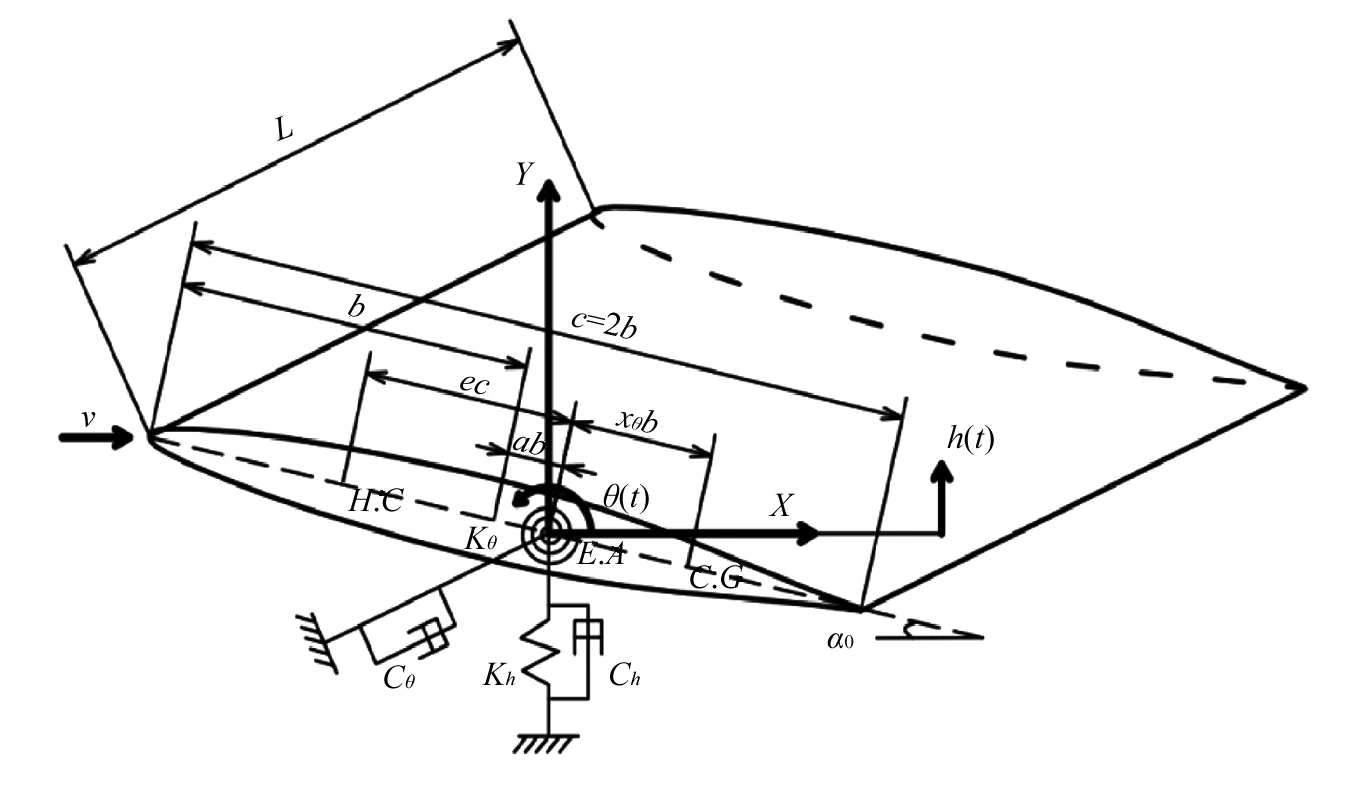
图1 两自由度三维水翼模型Fig.1 The three-dimensional hydrofoil with 2DOF

水翼弦长c=2b，展长为L，来流速度为v，初始攻角为α0。E.A为三维水翼弹性中心，位于翼弦中点后ab处，a为弹性中心到水翼弦长中点距离的无量纲量，定义弹性中心靠近随边，a为正弦长，b为半弦长。翼型在弹性轴处由一个线弹簧和一个扭转弹簧支撑，垂向位移h(t)与扭转角θ(t)均以弹性轴为参考点测量的，h(t)向上为正，θ(t)逆时针为正，在模态上分别对应水翼的第一弯曲模态和第一扭转模态。H.C为水动力中心，是流体作用力合力的作用点，位于弹性中心前缘eb处。重心C.G位于弹性中心后缘xθb处，xθ为重心到弹性轴的无量纲距离。

Woolston等试验研究了质量比对翼型稳定性的影响，翼型为NACA 16-010，材料为桃木，弦长c=0.305 m，展长L=1.219 m。试验的流体介质是空气和氟利昂的混合物，通过改变空气和氟利昂的比例来改变流体的密度，质量比μ=m/πρb2L,m为机翼的质量，ρ为流体介质的密度,在本次计算中，流体介质为水，水的密度不变，质量比是通过改变水翼的质量来实现的，模型的具体参数，如表1所示。

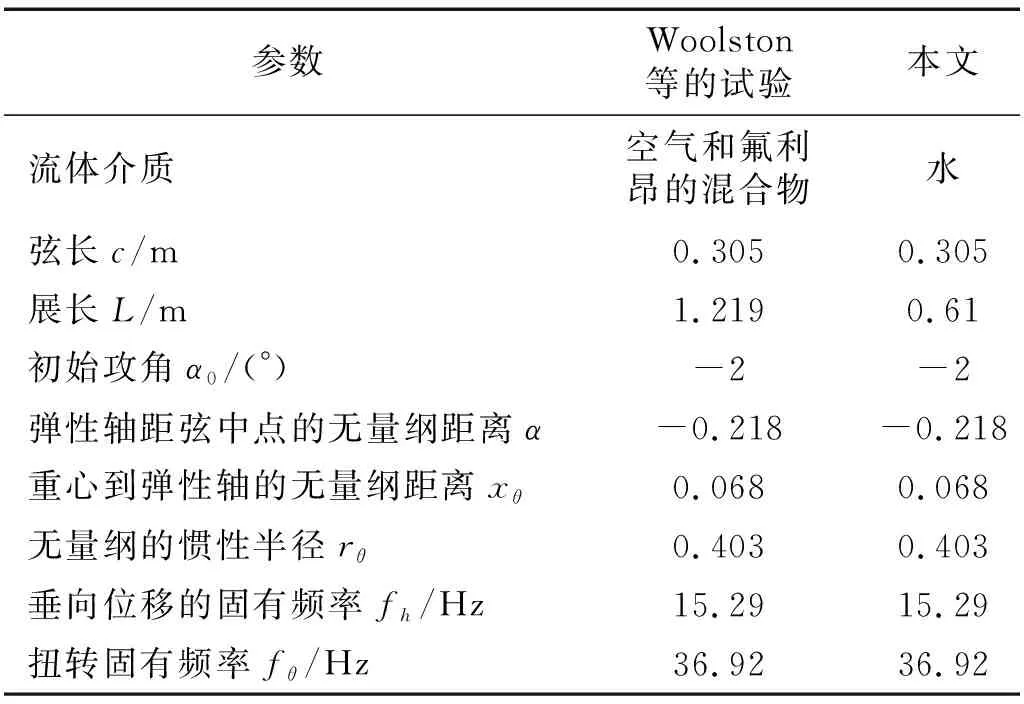
表1 Woolston和本文的模型参数Tab.1 Physical parameters of Woolston and this paper

在本文的验证工作中，参数选取与Woolston等试验模型的参数基本一致，在后面计算质量静矩和惯性矩对振动的影响时，主要计算质量静矩半径xθ和惯性矩半径rθ对振动以及噪声的影响。

1.2 两个自由度刚体的运动方程

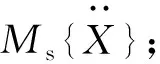
(1)

式中：{Ffluid}=[LfluidMfluid]T，Lfluid，Mfluid分别为水翼受到的升力和绕弹性轴的力矩；{X}=[hθ]T,h为水翼的垂向运动位移，定义向上为正；θ为水翼绕弹性轴的扭转角，定义逆时针为正。

(2)

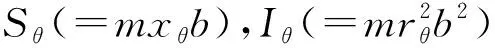
水翼的运动方程组是一个质量耦合方程组，水翼两个自由度的方程实际上是靠xθ和rθ耦合在一起，因此，xθ和rθ会对水翼的振动产生较大影响。求解水翼的振动必须先求解水翼的受力，水翼的受力通常可以用理论公式或CFD(Computational Fluid Dynamics)计算，理论方法一般用Theodorsen非定常理论在频域里求解，而CFD可以考虑黏性的影响，是在时域里采用流固耦合的方式求解水翼振动的时间历程信息。

1.3 流固耦合方法求解水翼的运动方程

本文采用时域法，用流固耦合的方式模拟水翼的流致振动，流体介质是水，流固耦合方式是在Fluent里用UDF实现的，流场在Fluent里求解，水翼的运动方程用UDF求解，并用UDF控制流场力和水翼位移的相互反馈。流场的计算是求解非定常的URANS方程，对于当前的计算，使用k-ωSST湍流模型可以达到一个较高的计算精度。

振动水翼在流场中的计算是一个相互影响的问题，由于本文的计算将水翼作刚性体考虑，不考虑结构变形，只考虑水翼位移，因此，在计算的过程中只需求解流体方程和刚体的运动方程，流体方程和刚体运动方程是交替求解的。耦合计算过程是在Fluent里采用UDF以动网格的形式完成，耦合计算过程如下：首先，Fluent迭代流场至稳定状态，将计算出的流场力传递给UDF，然后UDF根据水翼网格节点受力情况求出总的升力Lfluid和相对于弹性轴的力矩Mfluid，并求解两个自由度的运动方程，得到水翼的位移、速度和加速度并将位移传回流场中，流场网格更新，重新迭代至稳定状态，重复这个过程直到计算时间结束。两个自由度运动方程是采用四阶龙格库塔法求解的，对于流固耦合问题，流场和固体场要相互反馈信息，时间步长对计算精度有较大影响，在计算中将采取小步长和多迭代次数来保证计算精度。具体的计算过程如图2所示。

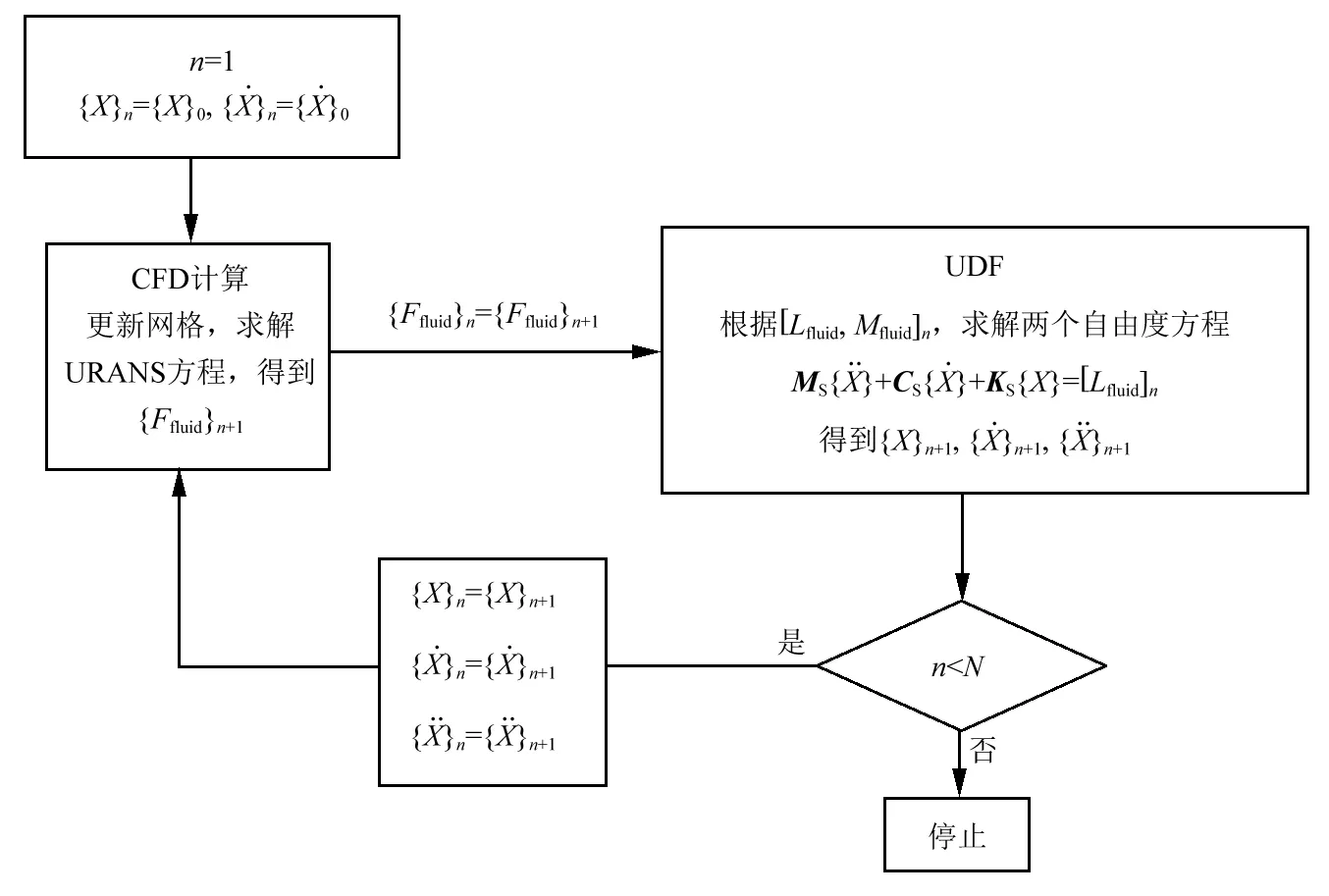
图2 计算流程图Fig.2 Coupled algorithm flow chart

流固耦合方法是在时间范围内模拟水翼振动的，能得到水翼的振动曲线，可求解水翼的一般振动和发散问题。临界速度是指刚好出现颤振或发散时的来流速度，判断依据是通过观察水翼振动的时间历程信息得到，当速度增加到一定值时，刚好出现位移和力的振动曲线的振幅随时间不发生变化，此时的速度为颤振的临界速度；当刚好出现位移和力随时间不断增大，不产生简谐运动，此时对应的速度为发散临界速度。

2 计算结果分析

2.1 网格无关性与时间步长的验证

流场的计算网格如图3所示。采用结构网格和非结构网格结合的形式，边界层采用结构网格以保证计算精度，远场网格采用结构网格以减少网格数量，边界层与远场之间采用非结构网格以实现网格的变形。边界层的y+接近1，并对远场的尾流区进行了加密。

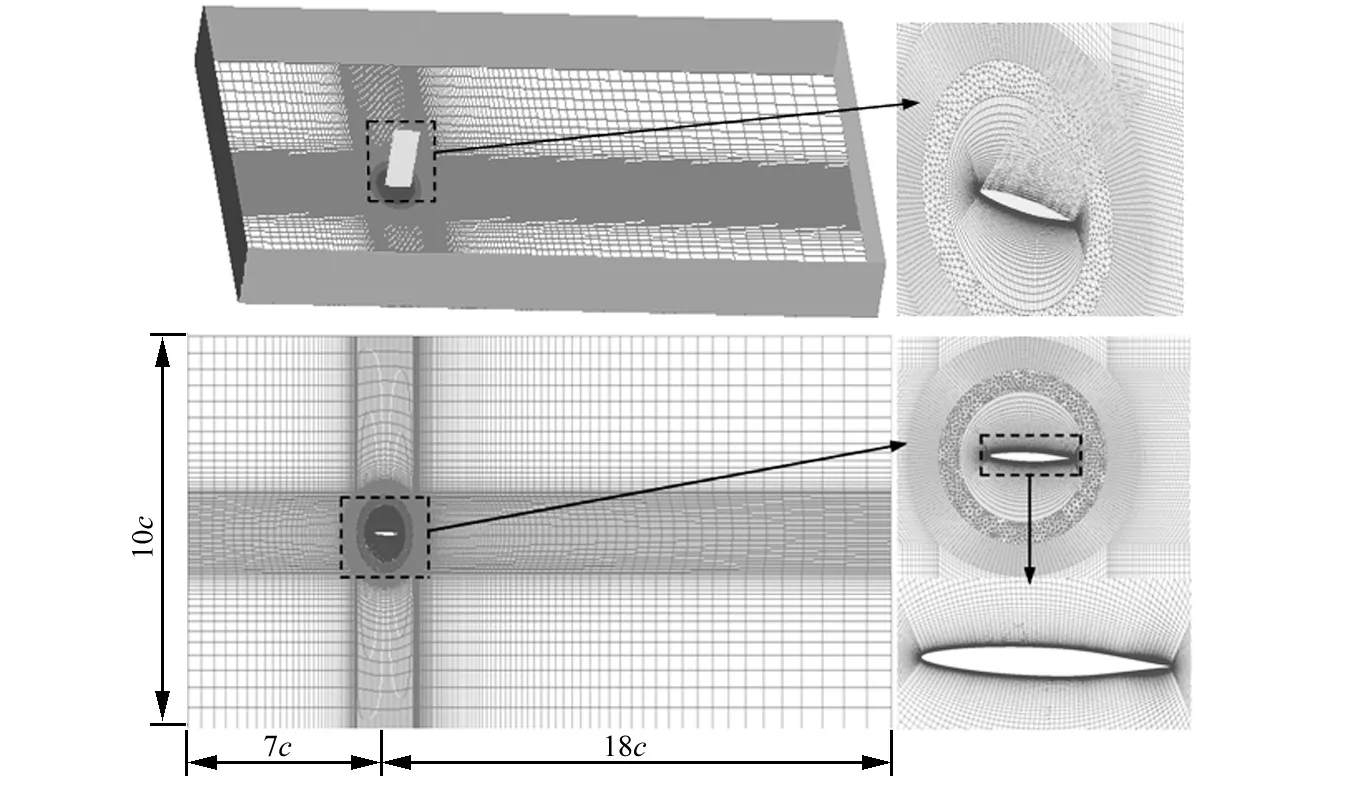
图3 流场计算网格Fig.3 Mesh of hydrofoil

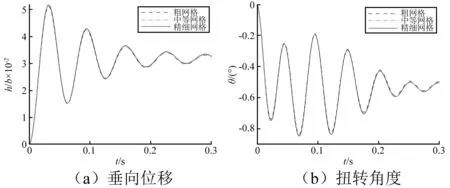
图4 网格无关性的验证Fig.4 The test of mesh

对于流固耦合的数值计算，时间步长对计算结果影响很大，如果时间步长偏大，会带来较大的计算误差，甚至有可能出现完全不同的计算结果，因此，有必要验证时间步长的合理性。在时间步长的验证中，选取三个时间步长计算，三个时间步长分别为dt=0.001，满足T/dt>50；dt=0.000 5，满足T/dt>100；dt=0.000 2，满足T/dt>200。计算结果如图5所示。从图5可知，相对于网格数量，时间步长的影响更大，特别是对扭转角的计算。理论上讲，小的时间步长可以得到更高的计算精度，dt=0.000 5与dt=0.000 2的计算结果比较接近，考虑到计算耗时问题，在后面的计算中，一般都选取dt=0.000 5为计算时间步长，但对于流速较大的计算，采用dt=0.000 2来计算，以保证计算精度。

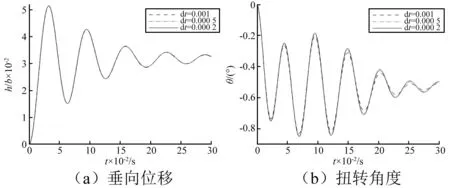
图5 时间步长的验证Fig.5 The test of time step

2.2 临界速度与质量比的关系

图的振动曲线(收敛状态)Fig.6 Vibration curves of

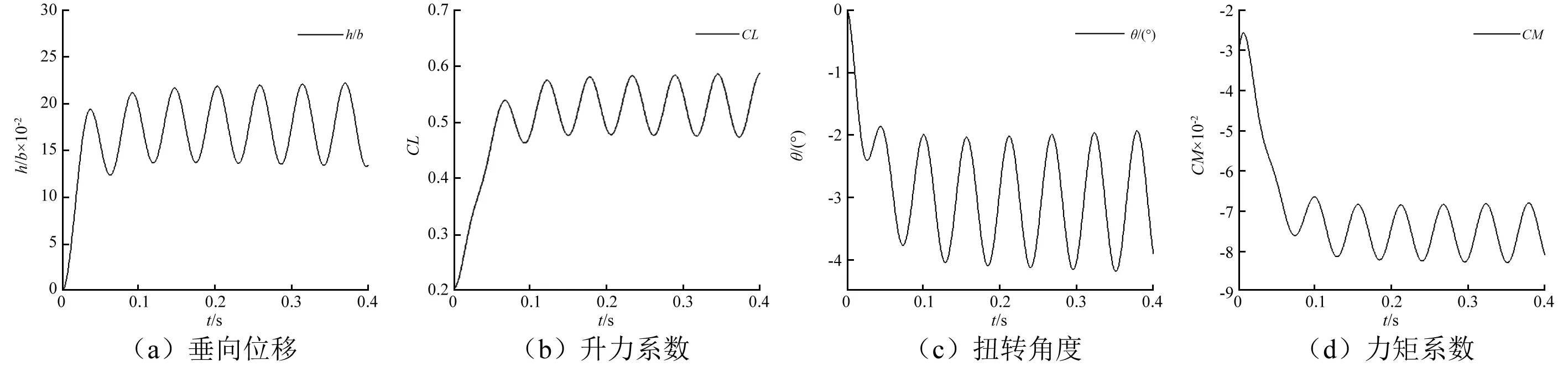
图的振动曲线(临界状态)Fig.7 Vibration curves of (critical state)

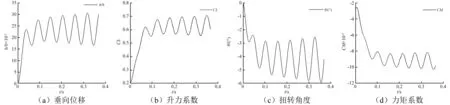
图的振动曲线(颤振状态)Fig.8 Vibration curves of

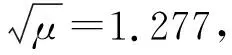
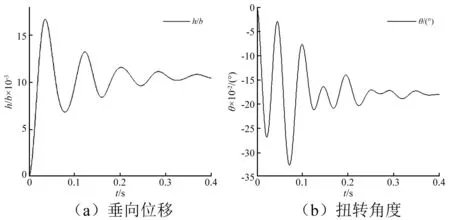
图的振动曲线(收敛状态)Fig.9 Vibration curves of

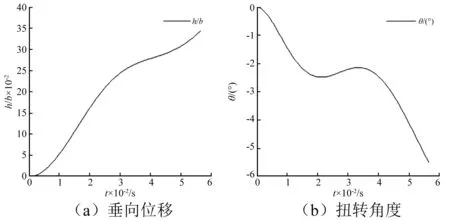
图的振动曲线(发散状态)Fig.10 Vibration curves of

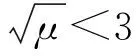
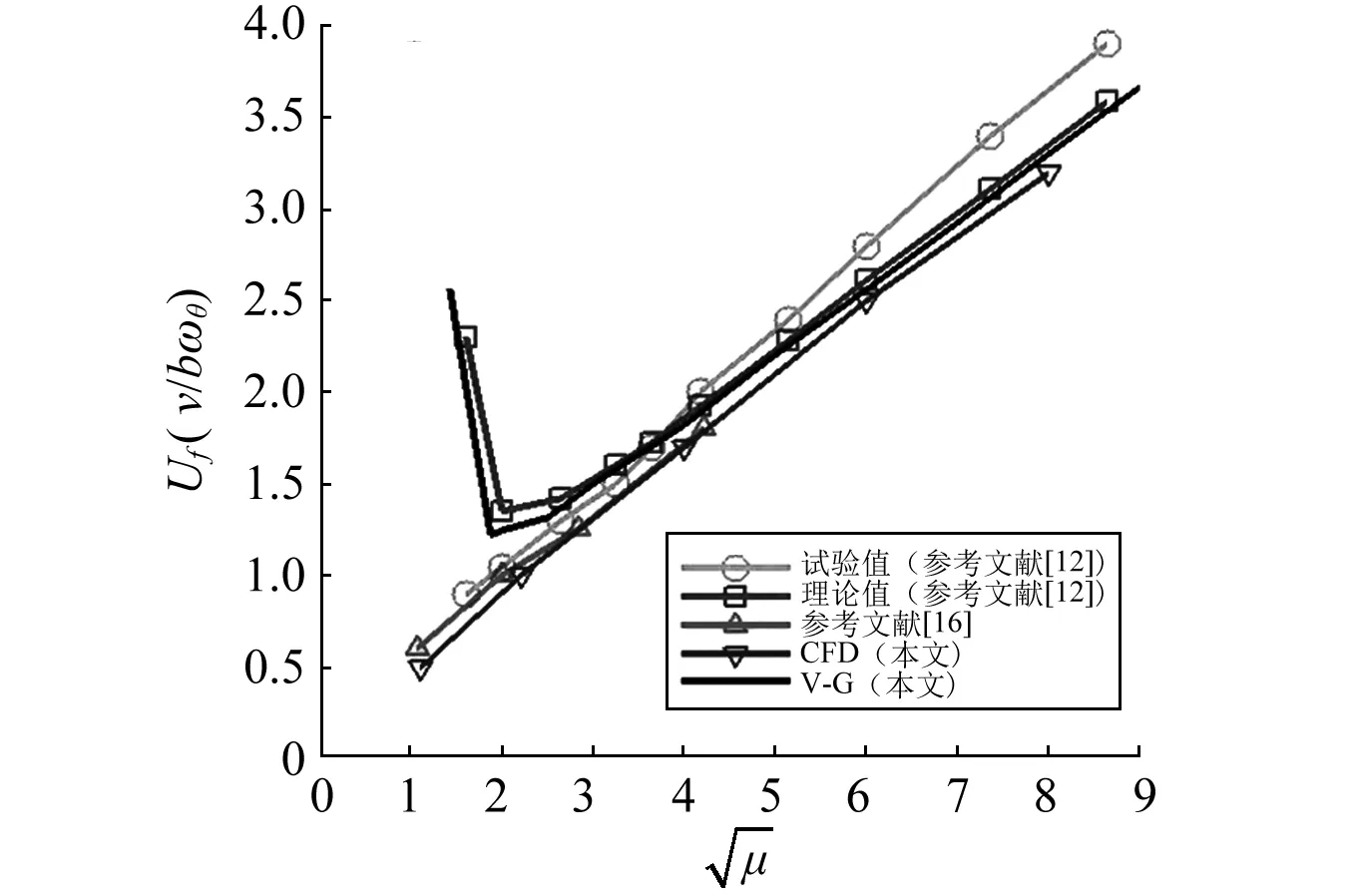
图11 临界速度与相对质量比的关系Fig.11 The relationship between critical velocity and added mas rate

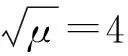
v-g法可以在频域里快速的提供一个理论解，对于高质量比，v-g法提供的理论解具有参考价值，但它不适用于发散问题，且不能提供振动的时间历程信息，对于水翼问题，一般质量比都较小，出现发散的概率大，同时，对于水动力问题，黏性也是不可忽略的因素。流固耦合的方法很好的弥补了v-g法的缺点，可以更真实的模拟水翼的振动，这也说明用流固耦合方法求解水翼振动问题是非常有意义且必要的。

2.3 质量静矩和惯性矩对振动状态的影响

在计算质量静矩对水翼流致振动的影响时，惯性半径保持不变，rθ=0.403，在U=1.4时，计算了三种状态，分别对应的无量纲静矩半径xθ为0.068，0.1和0.2。质量静矩对振动周期基本没有影响，其主要影响振动的幅值，质量静矩增大一定程度时，水翼的振幅会增加，当静矩增加过大时，振动反而衰减的更快，这可能是质量分布不对称，扭转会衰减的更快，从而加速整体的衰减，如图12所示。在计算xθ=0.1和xθ=0.2两种情况的临界状态时发现，xθ=0.1对应的临界速度Uf=1.53，其临界状态的振动曲线，如图13所示。在来流速度U=1.53时，水翼振动刚好处于临界状态，振动不增大也不减小；xθ=0.2对应的临界速度Uf=1.59，其临界状态的振动曲线，如图14所示。前面计算的xθ=0.068所对应的临界速度Uf=1.7，由此发现，质量静矩会影响水翼的临界速度。U=1.6时，对比xθ=0.1和xθ=0.2的振动曲线发现，在颤振状态下，质量静矩对垂向位移影响较小，而对扭转位移影响较大，xθ=0.2的扭转幅值明显比xθ=0.1的大,如图15所示。

在计算质量惯性矩对水翼流致振动的影响时，静矩半径保持不变，xθ=0.068，在U=1.7时，计算了三种状态，分别对应rθ=0.35，rθ=0.403和rθ=0.45。对于垂向位移，惯性矩主要影响振动频率，rθ增大，振动频率会降低；对于扭转角度，惯性矩主要影响振动频率和振幅，rθ增大，振动频率会减小，其减小趋势比垂向振动频率减小趋势要大，当rθ过大时，振幅会变小，如图16所示。由此可见，减小rθ会使fh与fθ的差距增大，因而要达到颤振临界状态(即fh=fθ)，就必须使速度增加。U=1.8时，水翼刚好发生颤振，说明rθ=0.35的临界速度Uf=1.8，如图17所示。在计算rθ=0.3的临界速度时，发现在U=1.95时，刚好出现了发散而没有出现颤振，这可能是由于fh和fθ差别过大，在两者频率相等之前，水翼的位移过大，以致发生破坏，如图18所示。

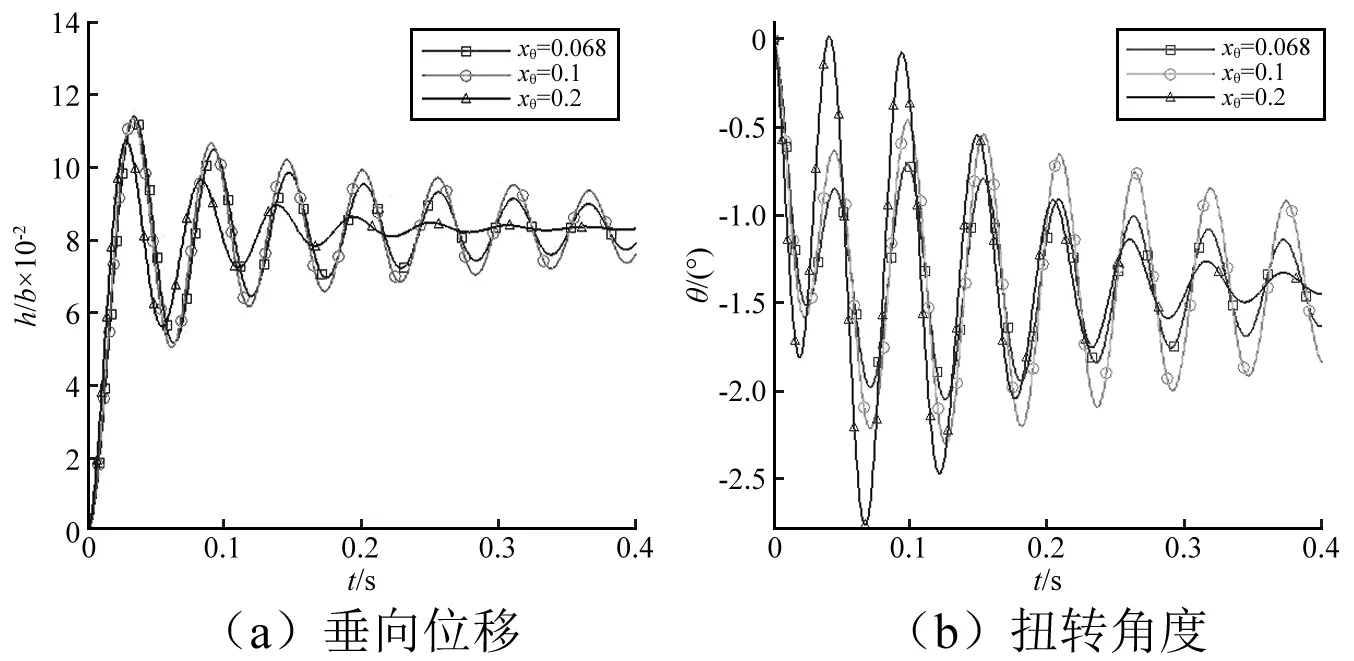
图12 质量静矩对振动的影响,U=1.4Fig.12 The impact of mass moment to the flow induced vibration,U=1.4

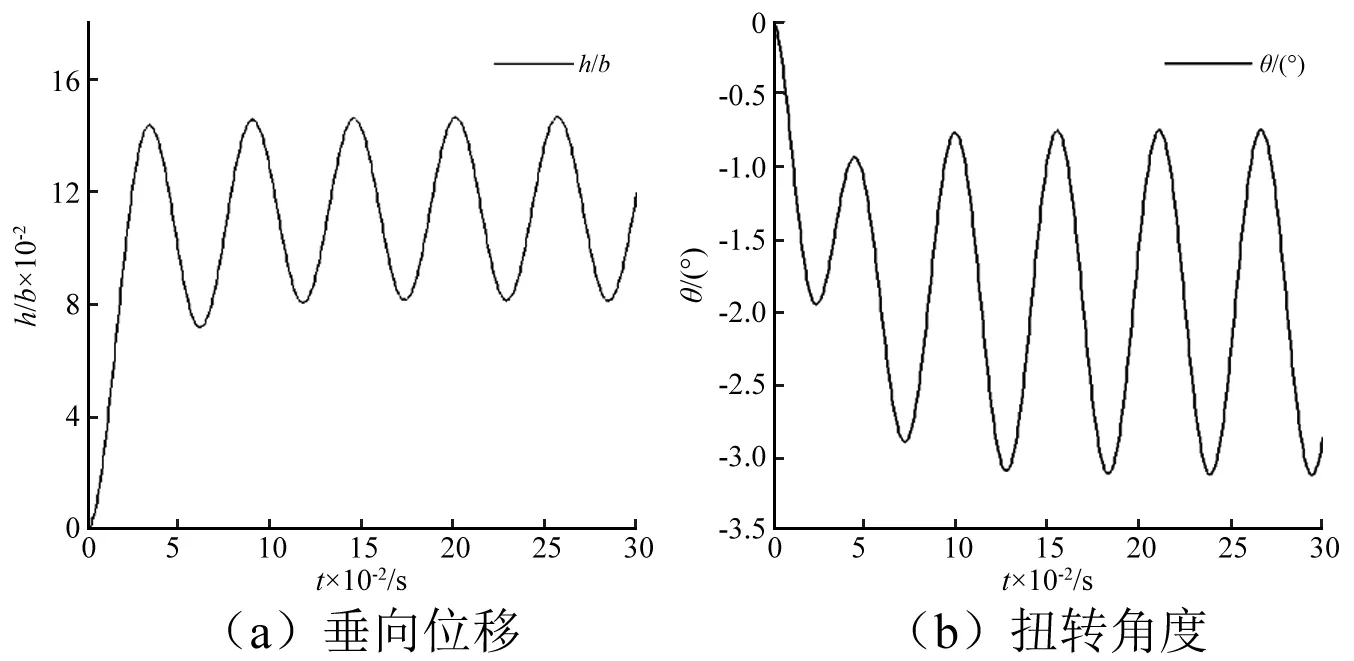
图13 xθ=0.1,Uf=1.53对应的振动曲线Fig.13 Vibration curves of xθ=0.1,Uf=1.53

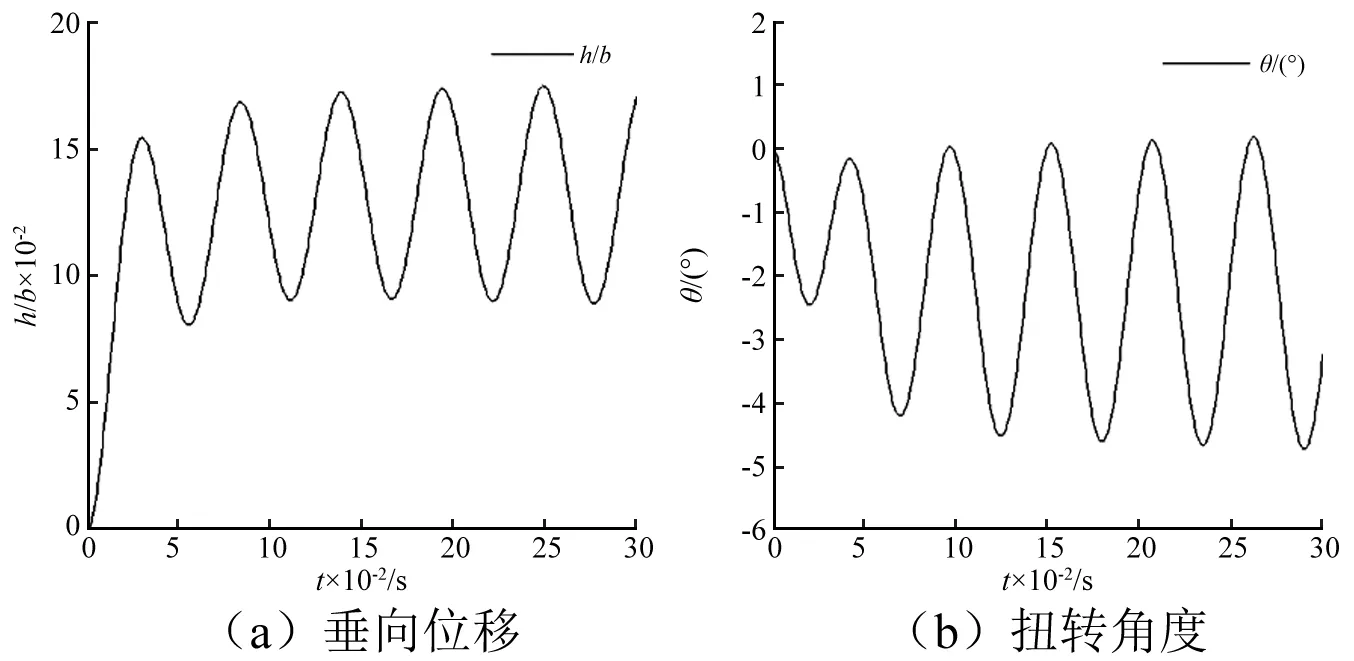
图14 xθ=0.2，Uf=1.59对应的振动曲线Fig.14 Vibration curves of xθ=0.2，Uf=1.59

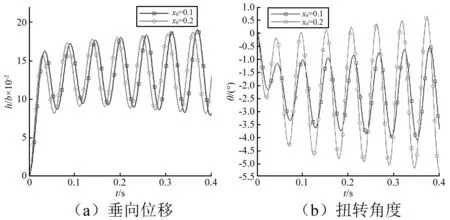
图15 xθ=0.1,xθ=0.2,U=1.6对应的振动曲线Fig.15 Vibration curves of xθ=0.1,xθ=0.2,U=1.6

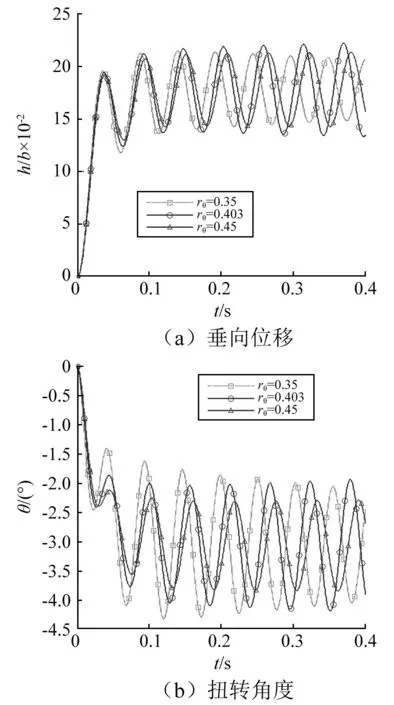
图16 质量惯性矩对振动的影响，U=1.7Fig.16 The impact of mass moment of inertia to the flow induced vibration U=1.7

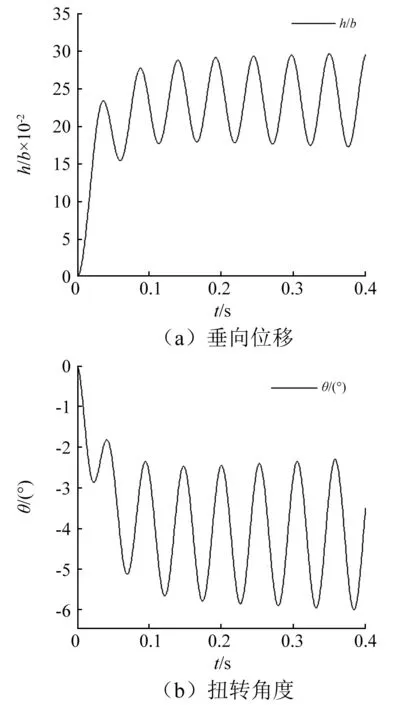
图17 rθ=0.35,Uf=1.8的振动曲线Fig.17 Vibration curves of rθ=0.35,Uf=1.8

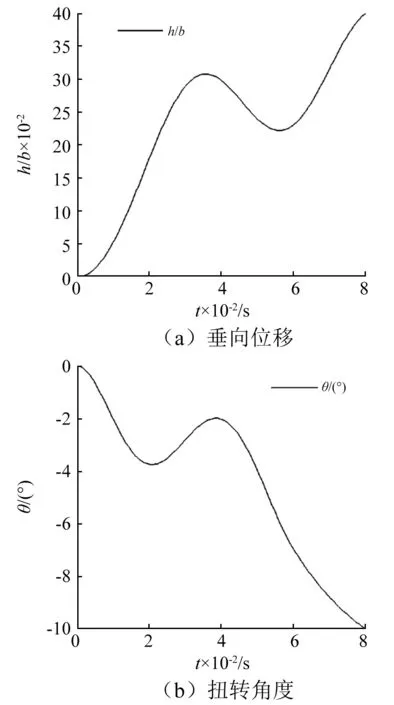
图18 rθ=0.3,U=1.95的振动曲线Fig.18 Vibration curves of rθ=0.3,U=1.95

3 振动水翼的噪声分析

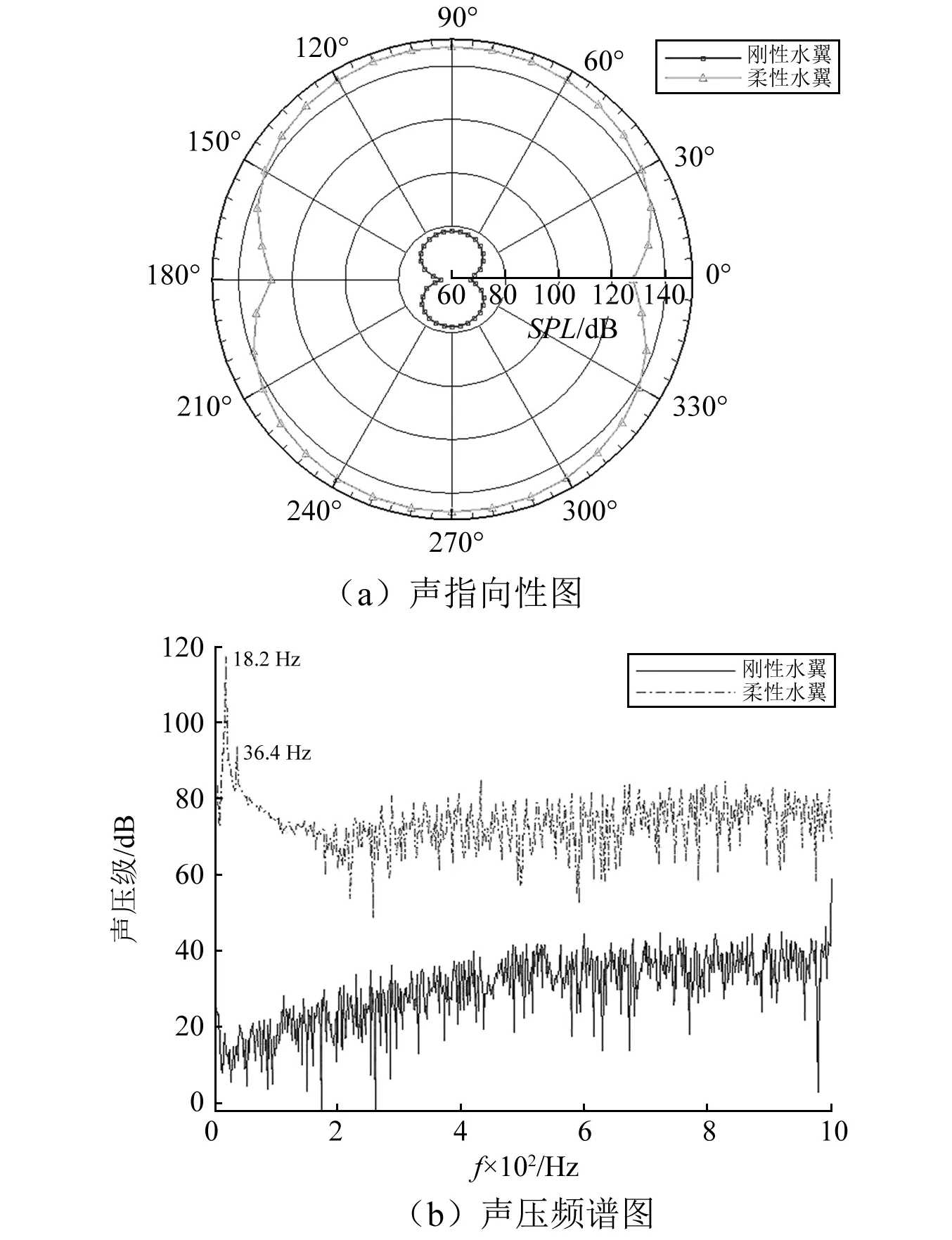
图19 固定翼和振动翼的声幅射对比图，U=1.7Fig.19 The sound radiation characteristics of fixed and flexible hydrofoil,U=1.7

研究质量静矩对噪声的影响时，其他参数不变，计算了xθ=0.068和xθ=0.1在U=1.7时的噪声。从前面的计算结果可知，xθ=0.068(其临界颤振曲线见图7)和xθ=0.1(其临界颤振曲线见图13)所对应的临界速度分别是Uf=1.7和Uf=1.53。在U=1.7时，两者都处于颤振状态，从图20(a)可知，在首尾两点的声压值比较接近，但是，在其他位置，xθ=0.1的声压值都比xθ=0.068的声压值大。从图20(b)可知，xθ=0.1的主峰值比xθ=0.068的主峰值稍微大一点，对于次波峰值，xθ=0.1的明显比xθ=0.068的大。前面计算质量静矩时发现，xθ=0.1对应的临界速度低且振幅大，综合噪声的计算结果，可以说明，在相同条件下，振幅越大，其对应的噪声也越大。

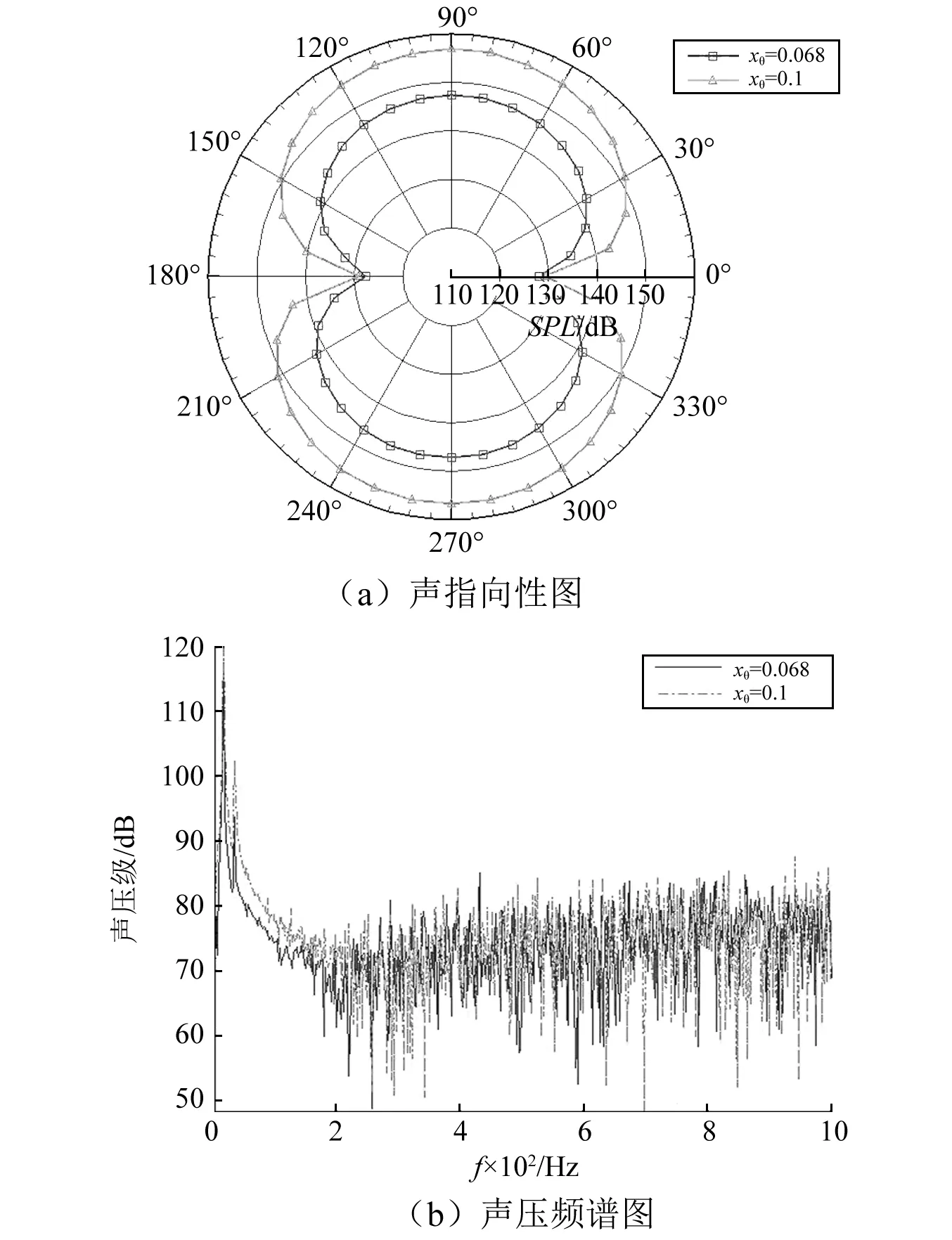
图20 xθ=0.068,xθ=0.1临界状态下的声辐射对比图，U=1.7Fig.20 The sound radiation characteristics of the hydrofoil (xθ=0.068，xθ=0.1),U=1.7

研究惯性矩对噪声的影响时，其他参数不变(见表1)，计算了水翼惯性半径为rθ=0.35和rθ=0.405在速度U=1.7时的噪声，从前面振动计算结果可知，rθ=0.35对应水翼的临界速度Uf=1.8，其临界颤振曲线，如图17所示，则，U=1.7时，rθ=0.35对应水翼的振动为收敛；rθ=0.405对应的临界速度Uf=1.7，临界颤振曲线，见图7。对比临界状态和收敛状态的噪声信息，如图21所示。临界状态下的噪声比收敛状态下的噪声大，收敛状态下的声压频谱图上只有一个波峰，对应其振动频率，而临界状态下的声压频谱图上有两个波峰，主波峰的峰值比收敛状态下的峰值高。

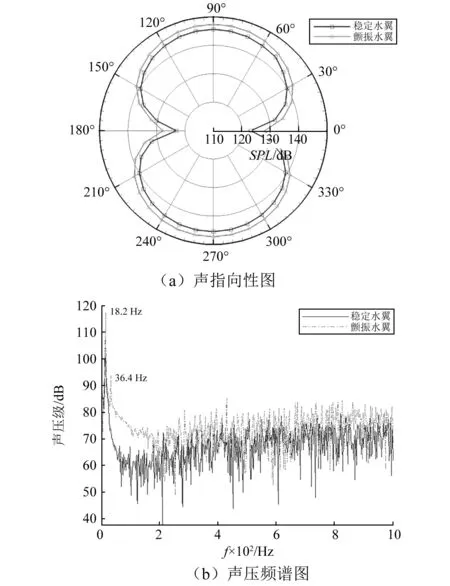
图21 临界状态和收敛状态的声幅射对比图，U=1.7Fig.21 The sound radiation characteristics of the hydrofoil,U=1.7

4 结 论

本文采用流固耦合的方法，用k-ωSST湍流模型数值模拟了两自由度三维刚性水翼NACA16-010的流致振动和声辐射问题。在一定范围内，CFD法计算水翼的临界速度与Theodorsen理论值和试验值比较接近，在水翼发散临界速度的计算上，Theodorsen理论会出现较大偏差，其原因是发散问题不满足Theodorsen理论解中的简谐运动假定。对于小质量比的水翼问题，出现发散的概率大，故采用流固耦合的方法求解水翼流致振动问题是非常有意义且必要的。

本文重点计算了质量静矩和惯性矩对振动的影响，从计算结果上看，静矩对振动频率影响较小，但对振动幅值影响较大，特别是对扭转角的幅值，同时临界速度也会随静矩发生变化；质量惯性矩对振动的频率和幅值都有影响，并且还会影响水翼的临界速度，有的情况下，惯性矩的改变还会使颤振水翼变成发散水翼。原因是水翼的运动方程是质量耦合的，质量静矩和惯性矩之间的关系对水翼的振动有重要影响。

最后，本文计算了水翼的声辐射问题，计算结果表明，水翼振动会使偶极子噪声显著增加，并且振动越剧烈，噪声增加的越多，在声压频谱图上会有一个与颤振频率相对应的峰值。