基于变分模态分解和独立成分分析的矿山微震信号降噪

2019-02-22黄维新刘敦文

振动与冲击 2019年4期

黄维新，刘敦文

(中南大学资源与安全工程学院，长沙 410083)

微震监测作为一种先进的地压监测手段，在矿山领域得到了越来越广泛的应用[1-4]。微震监测借助埋设的传感器接收岩体破裂等微震信号，再通过处理微震信号展开后续工作，因而微震信号的质量直接关系到后续工作的有效性。然而，矿井工作环境复杂，微震信号常与汽车运输、风机振动、凿岩冲击、放矿等噪音混合，这些噪音将对P波、S波初至拾取、震源定位和震源机制反演等造成影响。因此，开展微震信号去噪的研究具有重要意义。

微震信号具有随机性、非平稳的特点，基于傅里叶变换的降噪对周期信号效果较好，而对含尖峰和突变的微震信号适应性较差。近年来，小波和经验模态分解(Empirical Mode Decomposition, EMD)在微震信号降噪中的应用越来越广泛。例如：徐宏斌等[5-7]采用小波阀值对微震信号进行了降噪，而曹思远等[8]和Mousavi等[9]分别借助二代小波变换+阀值、同步压缩小波变换+阀值对微震信号去噪；梁喆等[10]和秦晅等[11]、Shang等[12]分别采用EMD与互信息熵、EMD与阀值对微震信号去噪。然而，基于小波变换的降噪，需选取合适的基函数和阈值才能达到较好的降噪效果；EMD是一种基于经验性的分解，其存在模态混叠、虚假分量等缺陷。梁喆等[13]采用基于LMS(Least Mean Square)自适应滤波器的LEMD(Empirical Mode Decomposition Based on LMS)方法对微震信号去噪，降低了EMD的端点效应。Han等[14]采用集合经验模态分解(Ensemble Empirical Mode Decomposition, EEMD)和阀值对微震信号去噪，降低了EMD模态混叠的影响。

VMD(Variational Mode Decomposition)作为一种新的信号分解方法，其具有严格的数学推导，能降低EMD模态混叠、虚假分量的影响[15-16]。然而，由于微震信号的复杂性，VMD得到的部分模态分量仍为噪音与有用信号的混合，直接舍弃或不做处理均不能取得较好的降噪效果。独立成分分析(Independent Component Analysis, ICA)能根据多个观测信号分离出相互独立的原始信号，然而其观测信号数须大于等于分离出的独立信号数目。为此，可将噪音与有用信号混合的多个模态分量作为ICA的观测信号，进而分离出有用信号，再与低频模态分量相加得到VMD_ICA降噪信号。此外，矿山微震信号常含有工频噪音，本文采用了一种正弦函数拟合的方法去除工频噪音。

1 降噪方法

1.1 变分模态分解

VMD理论假定待分解信号x(t)由有限个带宽有限、中心频率不同的模态分量组成。在各模态分量之和等于待分解信号的约束下，以求取各模态分量的估计带宽之和最小而构建的变分模型。与EMD得到的模态分量不同，VMD的模态分量均为调幅-调频信号，即

uk(t)=Ak(t)cos(φk(t))

(1)

式中：uk(t)为第k个模态分量；Ak(t)和φk(t)分别为uk(t)的瞬时幅值和相位。

VMD变分模型的建立过程如图1所示，其核心思想是构建式(2)所示的变分模型，并采用式(3)所示的Lagrange方程求解该变分模型。

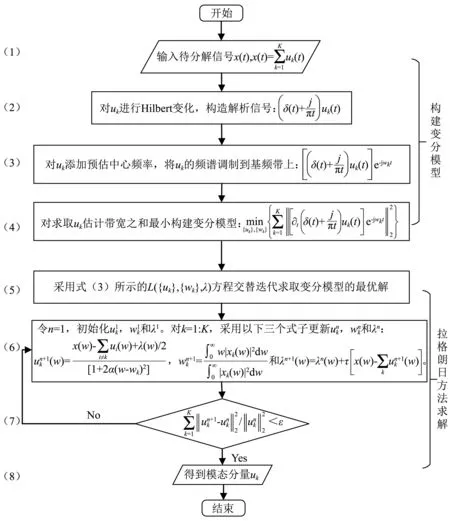
图1 VMD工作原理流程图Fig.1 Principle flow diagram of the VMD method

(2)

(3)

式中：wk为uk的频率中心；δ(t)为狄拉克函数；α为惩罚因子；λ为Lagrange乘法算子。

1.2 独立成分分析

1.2.1 ICA

独立成分分析从观测信号出发，借助信号的高阶统计特性，对混合信号进行估计分析，进而得到相互独立的近似源信号。假设M个观测信号X=[x1,x2, …,xM]由N个独立信号S=[s1,s2, …,sN]线性组合而成，则有

X=AS

(4)

式中：A为M×N阶矩阵，M≥N。

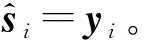
1.2.2 FastICA

本文采用Hyvarinen[17]提出的FastICA分离混合信号，其主要步骤如下：

步骤1 对观测信号中心化，使其均值为0；进而白化，得到标准化后的数据z；

步骤2 设定独立成分的个数N和收敛阀值ε；

步骤3 令分离矩阵W=[w1,w2, …,wM]T，初始化wi使W得的模为1；

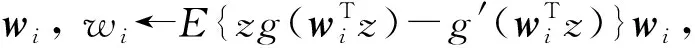
步骤5 对矩阵W正交化,W←(WWT)-1/2W；

步骤6 判断W是否收敛，若1-min{abs[diag(W(k+1)T)W(k)]}小于收敛阀值ε，则W为所求分离矩阵；反之，则继续步骤3～步骤6；

步骤7 由公式Y=WX求取独立分量。

1.3 VMD_ICA_Sine去噪

VMD能将信号分解至不同中心频带，最后几个模态分量通常为高频噪音，可采用相关系数法直接去除；中间的模态分量为有用信号与噪音的混合，采用ICA分离噪音和有用信号。此外，VMD_ICA不能去除工频噪音，提出采用正弦函数拟合去噪。相关系数和Sine函数定义分别为

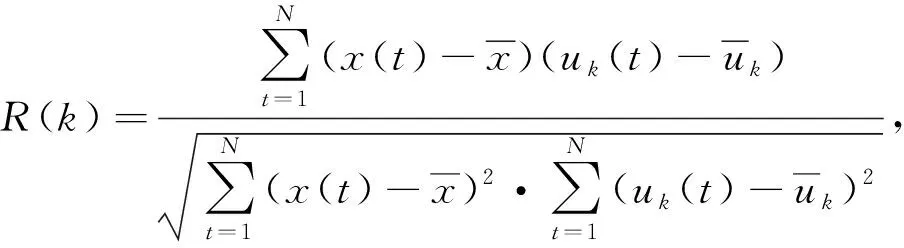
(5)

x′(t)=A0sin(w0t+φ0)+c

(6)

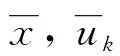
本文将上述VMD_ICA和Sine函数联合降噪简称为VMD_ICA_Sine去噪，其流程如图2所示，具体步骤如下：

步骤1 导入待去噪信号x(t)，t=1, 2, …,n, 其中，n为信号点的个数；

步骤2 采用VMD将x(t)分解为不同个数模态分量，再用主频差别法确定最佳模态分量个数；

步骤3 采用式(5)计算各模态分量与x(t)的相关系数，去掉相关系数较小的模态分量；

步骤4 采用相关系数适中的模态分量构建矩阵，再用FastICA分离噪音和有用信号；

步骤5 步骤4中提取的有用信号与剩余相关系数较大的模态分量相加，得到VMD_ICA去噪信号；

步骤6 采用式(6)拟合步骤5去噪信号的工频噪音，再用步骤5去噪信号减去正弦拟合信号得到VMD_ICA_Sine去噪信号。

图2 VMD_ICA_Sine去噪流程图Fig. 2 Flow diagram of the VMD_ICA_Sine denoising method

2 微震信号测试

2.1 VMD和ICA应用

以某矿微震信号为例(图3(a)中最上侧信号)，信号采样频率为6 000 Hz。采用VMD将该信号分解为2～8个模态分量，每个模态分量的主频如表1所示。由表1知：主频随模态分量序号增加而增大，模态数为7和8时，u2的主频不再下降。为此，本文确定将该微震信号分解为6个模态分量。

表1 不同模态数对应的主频

VMD分解得到的6个模态分量及其FFT幅值谱，如图3所示。采用式(5)计算得到u1～u6与原信号的相关系数分别为0.83,0.77,0.73,0.71,0.58和0.32，可见u6与原信号的相关系数明显小于其他模态分量的相关系数。此外，由图3易得u6几乎为随机噪音，而u2～u5仍含有部分有用信号(图中圈出部分及不太明显的尾部信号)。由此，直接舍掉u6，对u2～u5进一步提取特征。

将u2～u5作为观测信号，进而构建FastICA特征矩阵X，FastICA分析得到的独立分量IC1～IC4及其对应幅值谱，如图4所示。由图4可知，FastICA有效的将噪音与有用信号分离开来，提取到了P波初至信息特征。再将IC4与矩阵A对应的分量相乘得到具有实际幅值的有用信号，并与u1相加得到VMD_ICA降噪信号。

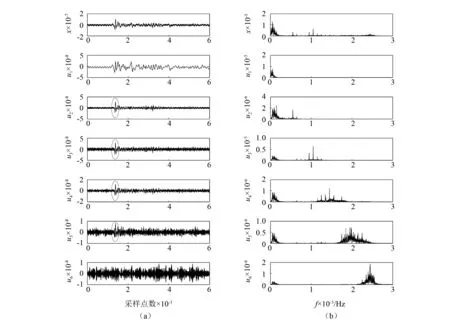
图3 微震信号VMD分解结果及其幅值谱Fig.3 VMD decomposition results of the microseismic signal and their corresponding amplitude spectra

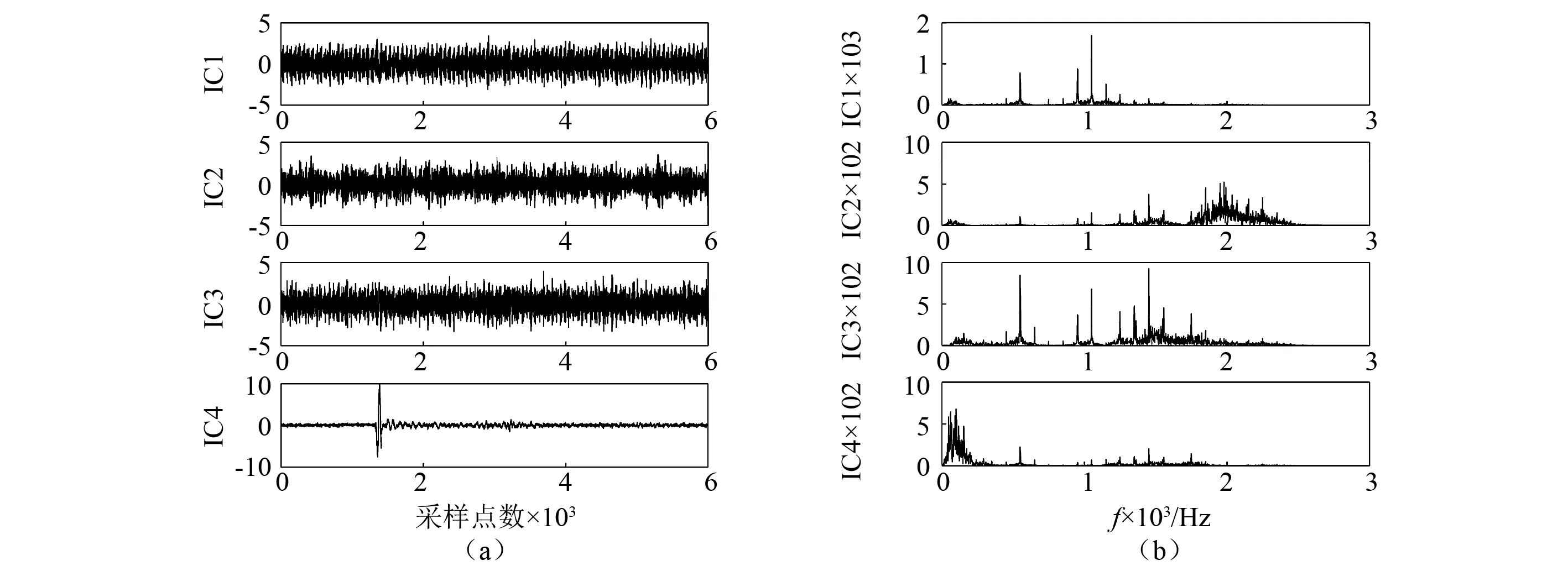
图4 ICA独立分量及其幅值谱Fig.4 Independent modes obtained from the ICA and their corresponding amplitude spectra

2.2 去噪效果

为测试VMD_ICA_Sine降噪方法的优越性，本文将舎弃噪音模态分量u6和噪音与有用信号混合模态分量u2～u5、舍弃噪音模态分量u6、VMD_ICA法和VMD_ICA_Sine法去噪信号分别绘于图5中。为定量的评价降噪效果，引入信噪比(Signal to Noise Ratio, SNR)，其定义为[18]

SNR=10 lg(σsignal/σnoise)

(7)

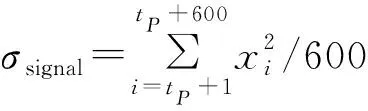
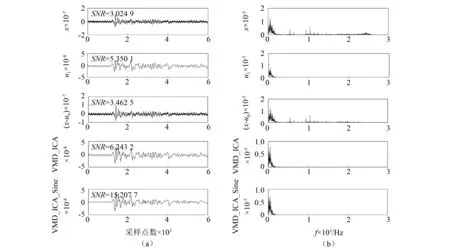
图5 不同方法降噪效果及其幅值谱Fig.5 Denoising performance of different methods and their corresponding amplitude spectra

由图5可知，不同降噪方法对SNR均有一定的提升，其中仅去除u6的降噪效果最差，仍含有大量高频噪音；舎弃u2～u6虽然得到了较好的去噪效果，但其相较于VMD_ICA法去噪，其P波初至等局部特征稍差；而VMD_ICA_Sine法有效的去除了工频噪音，同时很好的保留了P波初至信息。可见，VMD_ICA_Sine法具有较好的降噪效果。

3 微震应用

从某矿山微震监测系统中随机抽取1 938个微震信号，信号采样频率为6 000 Hz。采用PAI-K法拾取P波初至残差来评价降噪效果，PAI-K法借助P波初至前，微震信号主要为噪音，其高斯性很强，峰度值趋于零；而当P波初至时，非高斯性增强，取峰度值最大点作为P波初至。峰度值计算式[19]

(8)

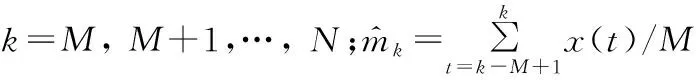
从上述1 938个微震信号中选取4个典型信号作为分析，其原始波形、VMD_ICA降噪波形和VMD_ICA_Sine降噪波形及其对应的峰度值序列，如图6所示，并将PAI-K拾取结果与原始波形人工拾取相比较，得到的拾取残差统计于表2中。

由图表知：PAI-K法对高信噪比信号(见图6(d))拾取效果均较好，但其可能受噪音和尾部信号影响(见图6(a)～图6(c))；VMD_ICA法能有效去除高频噪音和毛刺噪音，但其未能去除工频噪音(见图6(a))；VMD_ICA_Sine法可有效的去除工频噪音(见图6(a))，且其不受低频信号干扰(见图6(b)和图6(c))。

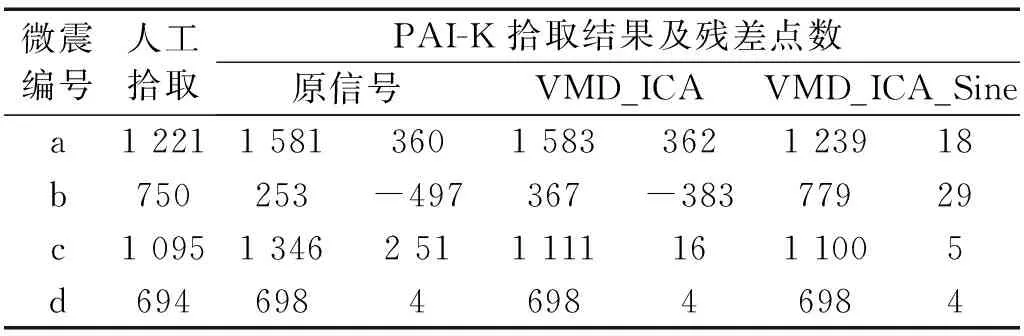
表2 典型微震信号PAI-K法拾取结果

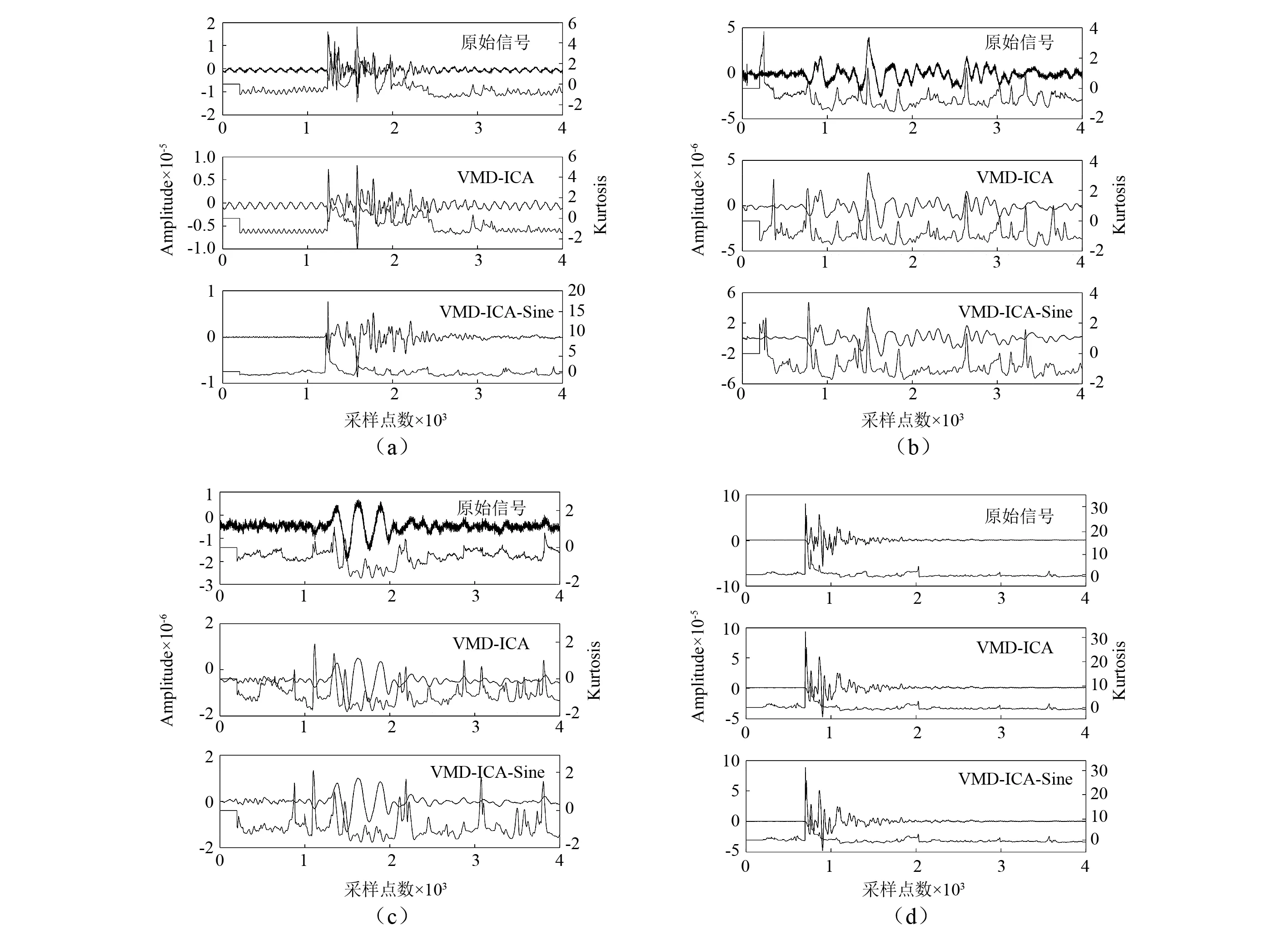
图6 典型微震信号PAI-K法拾取效果Fig.6 Picking performance for typical microseismic signals using the PAI-K method

将上述1 938个原微震信号及降噪微震信号的信噪比绘于图7中，图中SNR1，SNR2和SNR3分别指原微震信号、VMD_ICA降噪信号和VMD_ICA_Sine降噪信号的信噪比。由图7可知，VMD_ICA法和VMD_ICA_Sine法有效的提高了原信号的信噪比，且VMD_ICA_Sine法的信噪比优于VMD_ICA法。需要指出的是VMD_ICA_Sine法降噪与微震信号中含工频噪音的比例有关，笔者统计得到这1 938个微震信号中264个微震信号含有较明显的工频噪音。倘若含工频噪音微震信号的比例增加，VMD_ICA_Sine降噪效果会更好。

上述1 938个微震信号拾取残差如图8所示，拾取残差指PAI-K法拾取减去人工拾取。由图8可知，VMD_ICA法和VMD_ICA_Sine法降噪信号拾取残差为0～ 5 ms的微震信号数目明显高于原微震信号拾取数目，而拾取残差大于30 ms的微震信号数目小于原微震信号拾取数目，可见降噪后拾取效果优于原信号拾取效果。

进一步地，本文采用Li等[20]提出的定量方法评价P波初至拾取效果。该方法认为信号拾取误差越小，则惩罚值越小，并对所有信号的惩罚值求和，总惩罚值越小对应的方法越优。总惩罚值和惩罚值计算公式分别为

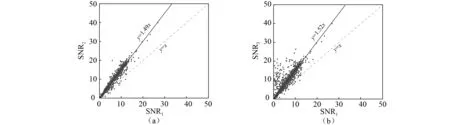
图7 原信号与降噪信号信噪比比较Fig.7 SNR comparison between original signals and denoised signals

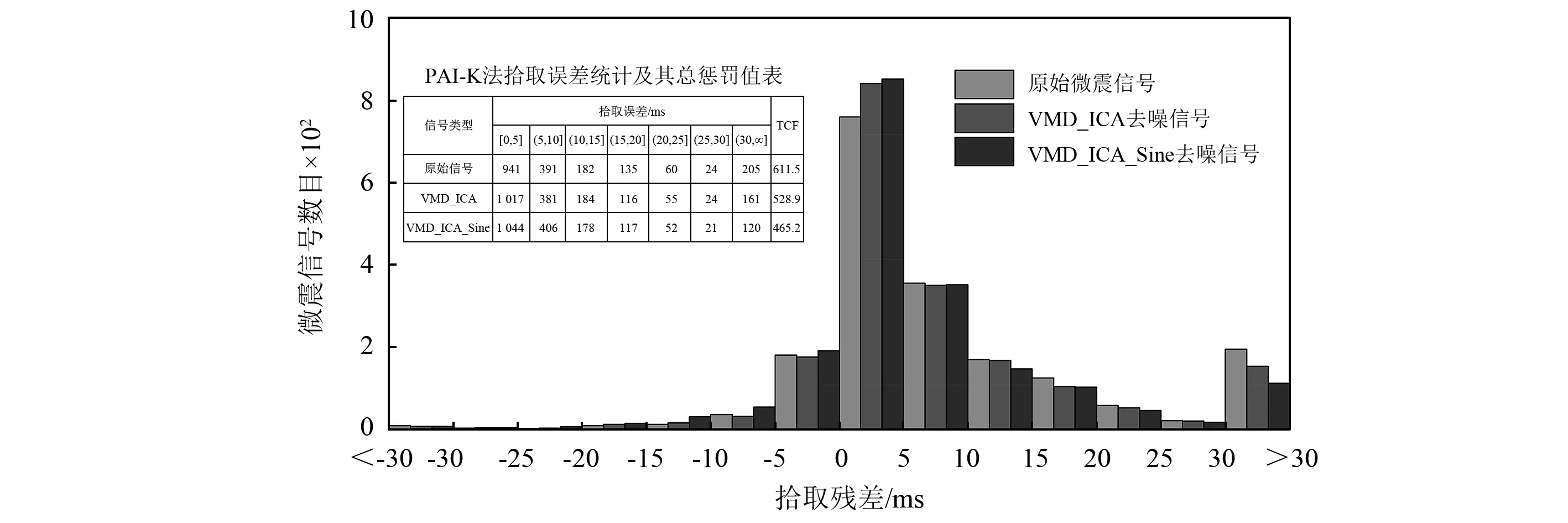
图8 原信号与降噪信号的PAI-K法拾取残差统计图Fig.8 Picking residual statistics for original signals and denoised signals using the PAI-K method

(9)

(10)

式中：Ci为微震信号i拾取的惩罚值，大括号右侧第1列为惩罚值，第2列为拾取误差范围。

计算得到原微震信号、VMD_ICA法和VMD_ICA_Sine法降噪信号拾取误差的总惩罚值TCF分别为611.5,528.9和465.2。由此可知，VMD_ICA_Sine法降噪信号拾取效果优于VMD_ICA法降噪拾取，且VMD_ICA降噪拾取优于原信号拾取，即VMD_ICA_Sine法能为矿山微震信号降噪提供了一种较好的分析方法。