基于频响函数综合的推进轴系动力学建模与支撑结构参数优化分析
2019-02-22黄修长苏智伟张振果华宏星
黄修长, 苏智伟, 倪 臻, 张振果, 华宏星
(1. 上海交通大学 振动、冲击、噪声研究所, 上海 200240;2. 上海交通大学 机械系统与振动国家重点实验室, 上海 200240;3. 上海交通大学 高新船舶与深海开发装备协同创新中心, 上海 200240)
推进系统产生及推进轴系传递的振动对船舶的振动噪声总体水平具有举足轻重的贡献,受到广泛关注[1-4]。目前已提出了各种主动或被动控制方法对推进轴系传递的振动导致的噪声进行控制,如轴上的RC共振变换器、周期结构和主动控制器;隔舱壁上动力吸振器;基座上的动力吸振器等,在各个针对性的控制频段内取得了较好的效果[5-9]。若能够在推进轴系设计时即通过对轴系支撑结构进行优化匹配设计,那么将获得事半功倍的效果。
在进行推进系统的设计时,主要考虑的是功率、效率、总体重量等因素,着重于船-机-桨的匹配;在轴系及其附件的设计时,进行轴系下轴承的刚度设计、高弹性联轴器的设计、推进电机下隔振器的设计时仍然以分开来考虑为主,轴承的设计主要考虑轴承的比压是否合理,高弹性联轴器主要考虑传递扭转、功率的因素,推进电机下隔振器也主要考虑电机本身的激励。除采用整体的有限元建模外,目前仍无一套有效的方法来对整个推进轴系耦合系统的振动传递及导致的声辐射进行有效快速地预报。轴承的刚度、高弹性联轴器的刚度、电机下隔振器的刚度匹配问题也无从谈起。
针对该问题,本文提出了基于子结构频响函数综合的子结构建模方法和灵敏度优化分析方法,获得了以振动传递最优时的各刚度匹配设计。
1 理论推导
1.1 基于频响函数综合的动力学建模方法
将螺旋桨激励下引起的船体结构声辐射问题分解螺旋桨激励下通过轴系传递至各个基座上的振动传递问题和在耦合系统中基座传递力激励下船体的振动声辐射问题。其中振动传递可采用基于频响函数综合的子结构方法进行动力学建模。将推进系统划分为螺旋桨(含水体)-轴系子结构A、电机子结构B、船体子结构(含水体)C;A和B之间通过高弹性联轴器连接,A和C之间通过轴承连接,B和C之间通过隔振器进行连接。激励力包括施加在螺旋桨桨叶0.7R处的螺旋桨三向推力和施加在推进电机质心处的六向激励力和力矩(R为螺旋桨半径)。建立物理模型如图1所示。

(a)综合前
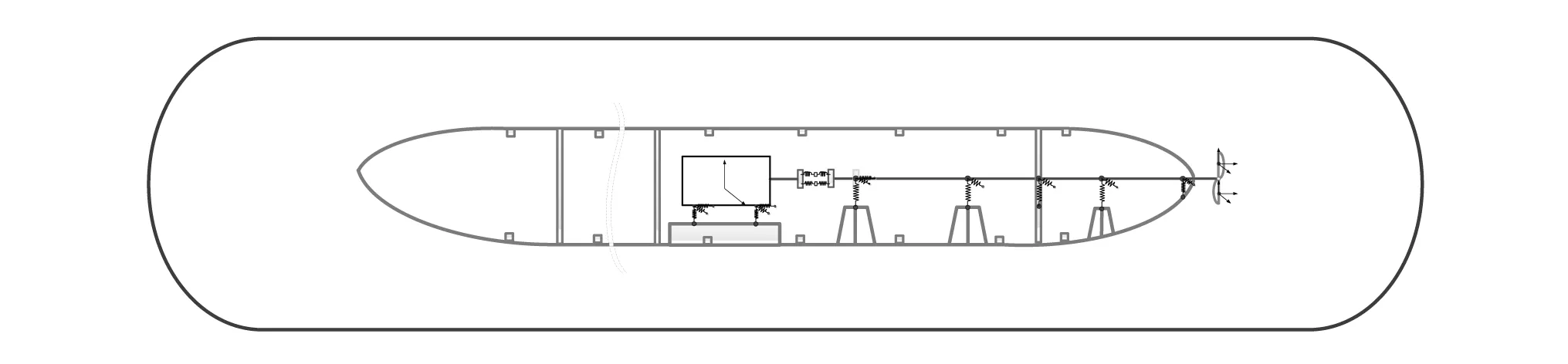
(b)综合后图1 推进轴系动力学建模的频响函数综合的子结构方法Fig.1 Dynamic modeling of a propulsion shaft system by FRF-based substructuring method

(1)
第一次综合后得到子结构体AB频响函数结果为
(2)
式中:各个矩阵的表达式请见文献[10]。
弹性联轴器采用6×6的阻抗矩阵进行描述
(3)
式中:6个方向的阻抗矩阵为(假设考虑高弹性联轴器的中间质量为mcp)
(4)

(5)

(6)
隔振器和轴承的三向阻抗矩阵为
Z
(7)
对轴承子结构,假设有nb个轴承,前nb-1个为艉后轴承或中间轴承,主要考虑垂向和横向刚度,第i个轴承的刚度和阻尼分别为
Z
(8)
式中:kk, yz和kk, zy为负且kk, yz≠kk, zy;dk, yz和dk, zy为负且dk, yz≠dk, zy。轴承子结构的阻抗矩阵为
(9)
且Zbe11=-Zbe12=-Zbe21=Zbe22。
对推力轴承,考虑三向刚度和阻尼为
(10)
由刚度阵和阻尼阵同样可得到推力轴承阻抗矩阵。
对隔振器子结构,假设有ni个隔振器,阻抗矩阵为

…kni,xx(1+iηni,xx)kni,yy(1+iηni,yy)kni,zz(1+iηni,zz)}
(11)

由计算得到的轴承上、下端,隔振器上下端各个连接点的位移,可以得到通过轴承和隔振器传递到船体结构的力为
(12)
从而得到输入给船体结构的功率流为
(13)
1.2 基于频响函数综合的子结构灵敏度优化方法
在对推进轴系的支撑结构刚度进行优化时,优化目标具有多种选择方案。实际上,船体结构的辐射声功率和船体表面的均方振速、输入到船体的功率流、传递到船体结构的均方力具有相同的频率特征以及随着频率的相对分布,考虑到以船体表面均方振速为优化目标时涉及表面振速的计算、以船体辐射声功率作为优化目标将涉及船体表面振速的计算以及已知表面振速下的声学计算,这需要存储从基座上连接点到船体表面所有点的传递函数、或存储从基座上连接点到远场声压的声传递向量,需要大量的计算消耗和存储空间。因此以通过轴承和隔振器传递到基座的传递力的均方值、输入到船体的功率流作为优化目标。
(14)
式中:ω1和ω2为优化带宽的频率下限、上限。优化变量为轴承的刚度、隔振器的刚度,优化变量的取值范围为初始值的-20%~+20%以内。采用子结构灵敏度优化方法对优化模型进行优化。由子结构连接点位移响应的表达式可得到响应相关的矩阵对轴承刚度、高弹性联轴器刚度、隔振器刚度和隔振器阻尼的灵敏度。部分响应对刚度参数的灵敏度表达式请见附录2。在获得了相关的响应对优化变量的灵敏度后,可以通过微分运算获得传递至基座的力、功率流对优化变量的灵敏度。每一步迭代过程中,沿着响应对当前参数的灵敏度方向进行搜索(灵敏度方向即响应对优化变量的梯度方向),寻找比前一迭代步的优化结果。为防止灵敏度优化时较早陷入局部最优解,在达到局部最优时进行反向搜索,直至搜索至边界,如图2所示。

图2 基于灵敏度的优化方法流程图Fig.2 Program flow chat for the optimization scheme
2 数值模拟及结果讨论
2.1 模型描述
以某一双体船为研究对象,双体船上有左右两套推进系统,轴系的总长为20 m,轴径350 mm,轴承包括艉后轴承、艉前轴承和推力轴承各1个。推进电机质量45 t,采用长方体质量块进行模拟,推进电机下有4个隔振器。轴承和隔振器刚度参数,如表1所示。轴承刚度采用基于流体动压润滑理论求得,所给刚度是轴承和轴承座的综合刚度,隔振器的刚度由实测得到。分析频段范围20~140 Hz,优化时也针对此频段内的结果进行优化。刚度优化的范围为初始刚度的-20%~+20%。
表1各个轴承、高弹和隔振器的初始刚度
Tab.1Initialstiffnessofbearingscouplingandisolators(N/m)

KxxKyyKyzKzzKzy艉后轴承1.75×108-2.79×1084.53×109-6.16×109艉前轴承1.92×107-1.78×1091.47×109-4.87×108推力轴承5.65×1082.34×108-1.28×1076.72×108-2.64×108隔振器1.06×1071.06×1071.768×107高弹1×1066.3×1066.3×106注:x, y, z分别为纵向、横向和垂向。高弹三个方向的扭转刚度Rx,Ry,Rz分别为1×106 N·m/rad, 0.25×106 N·m/rad, 0.25×106 N·m/rad
所施加的激励包括螺旋桨的激励力和电机质心的激励力。螺旋桨和推进电机的三向激励力分别采用宽带激励力经验公式和实测值给出,如图3所示。

图3 螺旋桨和推进电机三向激励力Fig.3 Propeller force and excitation force of the propulsion electric machine
2.2 建模结果及分析
首先进行子结构频响函数的计算。建立子结构A的流固耦合动力学模型,进行模态分析获得模态特性,由模态叠加法求得螺旋桨桨叶上0.7R处激励力施加点、艉后轴承、艉前轴承、推力轴承和高弹性联轴器之间的原点和跨点频响函数;采用刚体频响函数的解析计算公式获得子结构B上隔振器连接点和高弹性联轴器连接点之间的频响函数;建立子结构C的流固耦合动力学模型,在基座上轴承、隔振器连接点分别施加轴向、横向和垂向单位激励力的方法计算子结构C的基座上轴承、隔振器连接点的频响函数。基于频响函数子结构综合的方法获得系统的频响函数矩阵。
图4给出了考虑和不考虑轴承液膜交叉刚度时的响应结果,可见,考虑和不考虑轴承油膜交叉刚度时响应在峰值频率和峰值处响应幅值均有影响。低频的3个突出峰值是推进电机隔振系统的3向固有频率。图4标示出的33 Hz是螺旋桨-轴系-推力轴承的一阶纵振频率,48 Hz,56.5 Hz,71.5 Hz和86.5 Hz是螺旋桨的固有频率。可见,在螺旋桨和推进电机激励力共同作用时,响应仍然以螺旋桨-轴系-轴承的固有特性,特别是纵向固有特性为主,这是由于螺旋桨纵向激励力比较大的原因。

图4 有无交叉刚度螺旋桨和推进电机激励下的响应结果Fig.4 Responses for propeller forces and excitation by propulsion electric machine with/without bearing cross stiffness
以均方力和传递到基座的功率流为优化目标时,轴承原点刚度和交叉刚度、高弹、隔振器的刚度变化以及目标函数的变化,如图5和图6所示。可见针对目前的模型及参数:
(1)各个轴承的原点刚度变小,高弹的平移刚度和扭转刚度变大,隔振器的三向刚度变小对减小传递力和传递功率流有利;
(2)两个优化目标下,除轴承交叉刚度的变化趋势相反外,其它各个刚度变化趋势相同;
(3)最优值不是最后一个迭代步,在迭代的过程中会出现放大现象,这是由于在迭代时进行了反向搜索,避免陷入局部最优。

图5 以均方力为优化目标时刚度及目标函数变化曲线Fig.5 Variation of stiffness and objective function for mean-square force
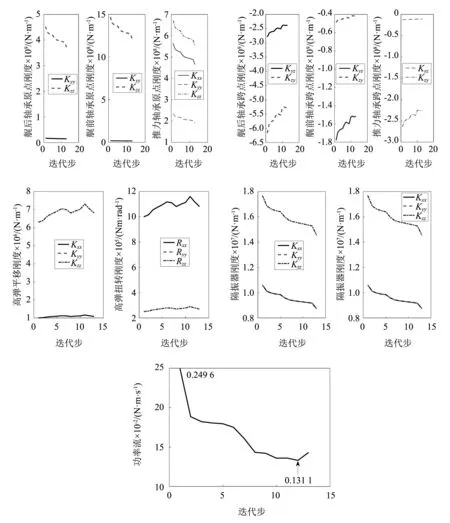
图6 以功率流为优化目标时刚度及目标函数变化曲线Fig.6 Variation of stiffness and objective function for power flow
从推进系统到船体的振动途径有2个,即各个轴承和推进电机下隔振器,传递的功率流,如图7所示。可见,在33 Hz以下频段内推进电机的激励能量占主,能量主要通过推进电机下隔振器传递;在33 Hz以及33.0~56.5 Hz频段和71.5 Hz,86.5 Hz峰值频率处,螺旋桨的能量占主,能量主要通过轴承进行传递;33 Hz以上的其它频段以隔振器传递为主。高弹是螺旋桨与推进电机的能量进行交换的重要通道。对推进电机与螺旋桨之间通过高弹传递的功率流进行分析发现,在功率流以轴承传递到船体占主的频段,功率流由推进电机端流向螺旋桨端;在功率流以隔振器传递到船体占主的频段,功率流由螺旋桨端流向推进电机端。

图7 通过隔振器、轴承和高弹(螺旋桨到电机)的功率流Fig.7 Power flow for isolators, bearings and coupling
以均方力和功率流为优化目标时,传递到基础的功率流,如图8所示。可见,33 Hz桨-轴系-推力轴承的一阶纵振频率处能量以及33 Hz以下频段推进电机激励能量占主的频率成分得到很大的降低,33 Hz以上频段螺旋桨峰值处的传递增加。优化结果表明通过隔振器传递的功率流需要得到更大的抑制,从而使得整个系统在所考虑的频段内传递到船体的功率流减小。因此,高弹的刚度增大,使得耦合增强,系统中更多的能量通过隔振器传递,并被更好地耗散掉,从而更加高效地抑制传递至船体的能量。从另一个角度,使整个系统通过减振器和轴承传递的能量分布更加均衡,避免某一传递通道能量过大。
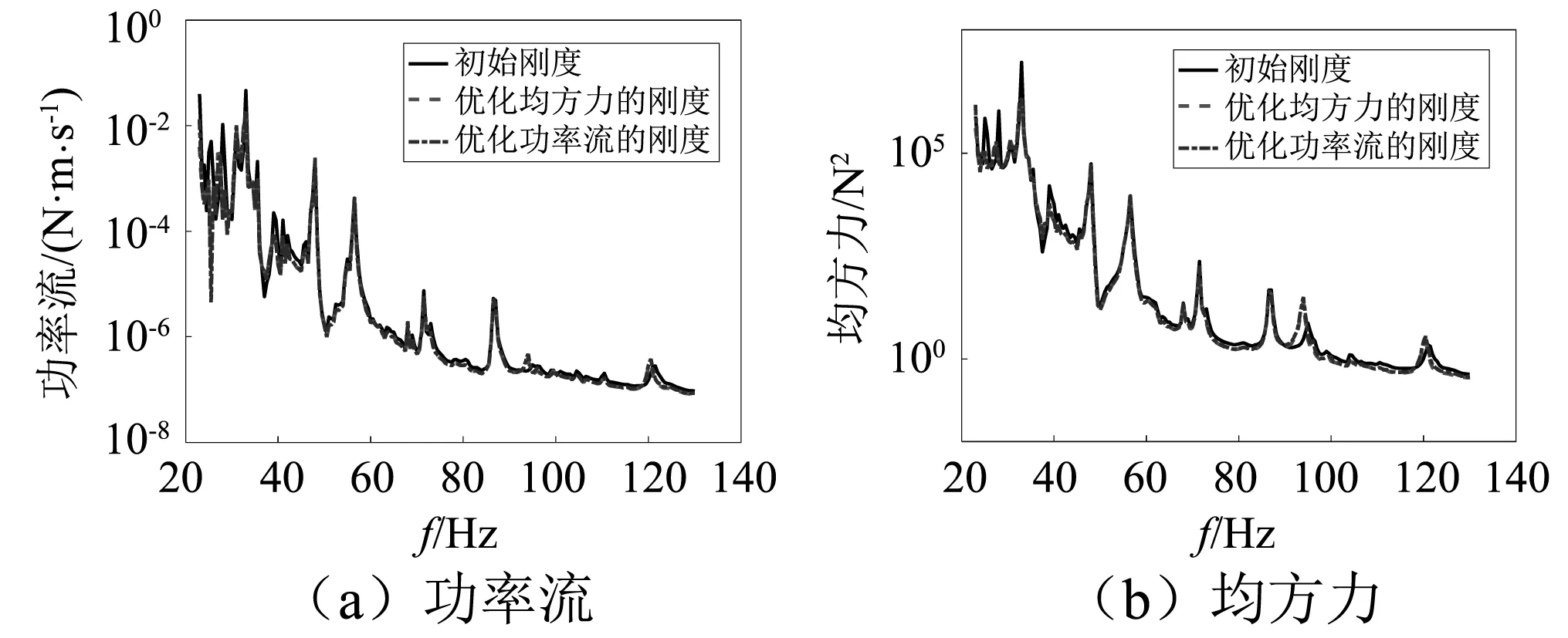
图8 各种刚度下传递至船体结构的功率流和均方力Fig.8 Power flow and mean-square forces under different stiffness
3 结 论
针对船舶推进轴系,提出了基于子结构频响函数综合的建模和灵敏度优化分析方法,获得了分别以传递到船体结构的均方力和传递到船体结构的功率流为优化目标的最优的各刚度匹配设计。得到以下结论:
(1)考虑和不考虑轴承油膜交叉刚度对响应的峰值频率和峰值处响应幅值均有影响。
(2)由于螺旋桨纵向激励力比较大,在螺旋桨和推进电机激励力共同作用时,响应仍然以螺旋桨-轴系-轴承的固有特性,特别是纵向固有特性为主。
(3)各个轴承的原点刚度变小,高弹的平移刚度和扭转刚度变大,隔振器的三向刚度变小对减小传递力和传递功率流有利。
