含负刚度器件的Maxwell模型动力吸振器的参数优化

郝 岩, 申永军， 杨绍普， 邢海军

(石家庄铁道大学 机械工程学院，石家庄 050043)

黏弹性材料在建筑、医学、机械和航天等工程领域的应用非常广泛，其模型一般可简化为Kelvin模型和Maxwell模型。在工程实际中，阻尼元件本身不可避免地存在一定的弹性，所以Maxwell模型更能代表工程实践中的黏弹性材料[1]。帅词俊等[2]提出了一种针对黏弹材料的KWW函数与广义Maxwell模型转换的计算方法，实现了对黏弹材料的广义Maxwell模型的拟合。张小兵等[3]采用广义Maxwell模型模拟玻璃模压仿真过程所表现的黏弹力学特性，研究结果对玻璃模压建模及非球面透镜的实际加工具有一定指导意义。文献[4]通过对Maxwell模型进行黏性系数非定常改进，现场试验研究应力波在完整岩体中的滤波特性。文献[5]对Maxwell黏滞阻尼耗能结构的两自由度体系的随机地震响应进行了分析，结果更为准确、简便。

动力吸振是振动控制常用的方法之一，通过动力吸振器(Dynamic Vibration Absorber，DVA)吸收主振动系统的能量来降低主系统的振动[6]。Frahm[7]发明了第一个无阻尼的动力吸振器，研究发现该模型的适用频率非常窄。Ormondroyd等[8]通过在DVA中加入阻尼发现能够有效抑制主系统振幅并适当拓宽减振频率，这种含有阻尼的动力吸振器就是目前广为所知的Voigt型DVA。同时Ormondroyd等首先发现了该动力吸振器的幅频曲线存在两个独立于阻尼的固定点，并据此提出了设计动力吸振器的固定点理论。Hahnkamm[9]根据该理论得到了吸振器最优调谐比的设计公式；随后，Brock[10]推导出了最优阻尼比的设计公式。实际上，上述结果是Voigt型动力吸振器的近似最优解而非精确解。Nishihara等[11-12]通过推导得到了精确解析解，发现根据固定点理论推导的结果与精确解析解非常接近。Ren[13]提出了一种新型接地式动力吸振器，并根据不动点理论推导得到了最优设计公式，结果表明相同质量比时该DVA能获得更好的减振效果。Liu等[14]采用另一种方法也推导出了相同的结果。为了进一步提高动力吸振器的减振效果，并且考虑到工程实际中大量使用黏弹性材料加质量块来构成DVA，Asami等[15-16]提出了三要素型动力吸振器并得到了最优设计公式，发现在相同质量比情况下，该模型具有更好的减振效果。文献[17-18]研究了四种半主动动力吸振器的近似解析解，并与数值解对比，分析了时滞对系统的影响和半主动动力吸振器的减振效果。

负刚度器件产生的力与位移的方向相同，具有承载能力大、变形小、可控性能好、固有频率低等优点。因此，近年来针对负刚度的理论和应用研究越来越多。Alabuzhev等[19]出版了第一部关于负刚度器件的专著，较全面地介绍了负刚度的实现形式及隔振系统的理论和应用。Platus[20]提出将负刚度器件应用于隔振器中，设计出一种准零刚度结构。彭献等[21]研究了含负刚度弹簧系统的隔振原理，并进行了能量分析。彭解华等[22]对正负刚度并联系统的稳定性问题进行了研究，发现采用正负刚度并联既能降低系统固有频率又能提高隔振效果。Acar等[23]提出了一种含负刚度的自适应动力吸振器，能够有效地降低系统振幅。文献[24]研究了一种含负刚度器件的新型动力吸振器的参数优化。文献[25]研究了含负刚度器件的三要素型动力吸振器的参数优化，表明含负刚度器件的动力吸振器能够取得很好的减振效果。文献[26]研究了一种含负刚度器件的线性振荡器的超阻尼特性，并对其进行动力学仿真分析。

本文首先将负刚度器件引入到黏弹性材料中的Maxwell模型，并将含负刚度器件的Maxwell模型加入到动力吸振器中形成一种含负刚度器件的Maxwell模型动力吸振器。其次，利用固定点理论和H∞优化准则对系统刚度和阻尼参数进行优化。最后通过与其它经典动力吸振器模型在简谐激励下的响应对比，说明了本文模型能够大幅降低系统共振区的振幅，同时也拓宽了减振频率，并验证了本文模型有较好的吸振效果。进一步在随机激励条件下同样证明了本文模型具有很好的减振效果。

1 动力吸振器模型及解析解研究

本文提出的含负刚度器件的Maxwell模型动力吸振器，如图1所示。其中m1为主系统质量；m2为动力吸振器质量；k1和k2分别为主系统和动力吸振器的刚度；k和c分别为Maxwell模型的负刚度和阻尼；F和ω分别为激振力振幅和频率；x1，x2和x3分别为主系统、动力吸振器以及串联负刚度弹性系统和阻尼分割点的位移。根据牛顿第二定律可以得到系统的动力学方程

(1)

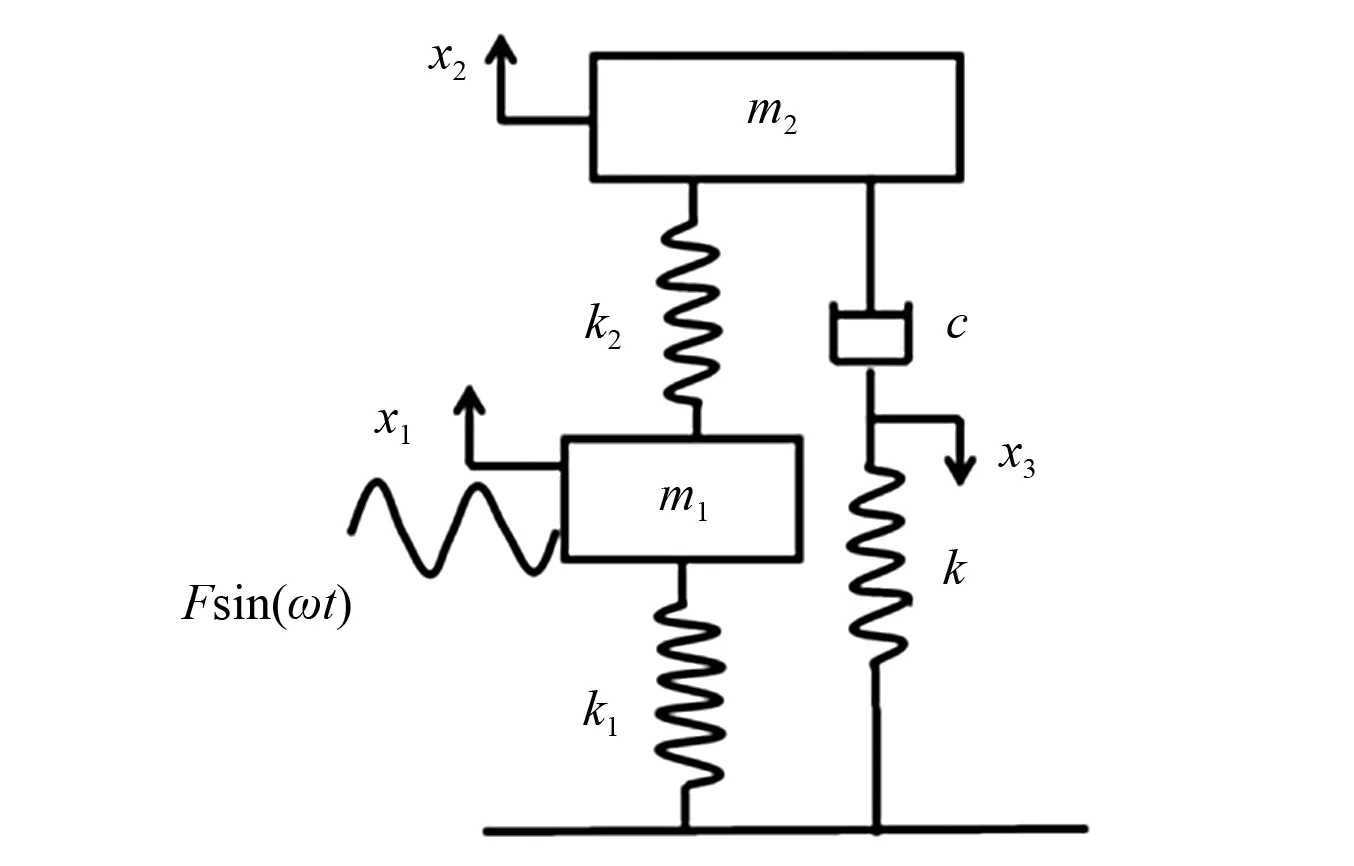
图1 含负刚度的Maxwell模型动力吸振器Fig.1 Maxwell model DVA with negative stiffness

引入以下参数

式(1)可化为

(2)

设

x1=X1ejωt,x2=X2ejωt,x3=X3ejωt

(3)

将式(3)代入式(2)解出

(4)

式中：j为虚数;其它参数为

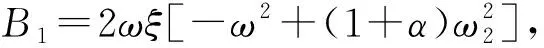
令

定义主系统振幅放大因子A

(5)

其中，

A2=αυ(λ2-υ2),
B2=2λ(υ2+αυ2-λ2),
C2=αυ[λ2(1+(1+μ)υ2)-λ4-υ2],
D2=2λ{λ4+(1+α)υ2+μαυ4-λ2[1+(1+α+μ)υ2]}

2 最优参数

由式(5)通过简单推导，可以证明系统归一化的幅频曲线都将通过三个独立于阻尼比的点，这三个点称作动力吸振器主系统幅频曲线的固定点。为了直观证明该结论，图2给出了阻尼比分别为0,38.24%和∞时的归一化幅频曲线。从图2和图3可知，曲线均通过P，Q，R三点。这里只是对数值进行了验证，在Ormondroyd等的研究中有类似的证明。根据固定点理论，为了使三个固定点纵坐标等值，只需使阻尼比趋于零和趋于无穷时的响应值相等，即

(6)

化简得到

λ6+a1λ4+a2λ2+a3=0

(7)

其中,

因为固定点与阻尼比无关，当ξ=0时，

(8)

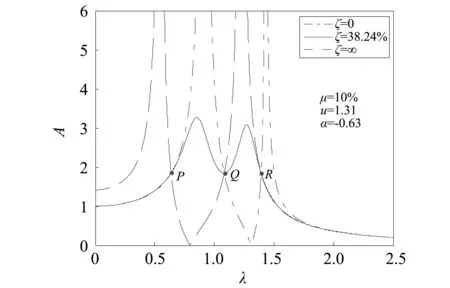
图2 不同阻尼比下归一化幅频曲线Fig.2 The amplitude-frequency curve under different damping ratios

当ξ=μ时，

(9)

所以为了求出P,Q,R三点的纵坐标，联立式(8)和式(9)得到

(10)

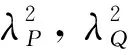
(11a)

(11b)

(11c)

当把三个固定点的纵坐标调到同一高度，就可以得到最优频率比，从而有可能使得幅频曲线的最大值最小化，这个调整需要两步完成。

第一步把P点和R点的纵坐标调整到同一高度，即

(12)

其中，

A3=(2+α)υ2,
B3=-2,
C3=αυ2(1+μυ2),
D3=-αυ2,

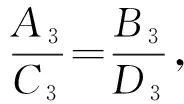
(13)

化简式(13)得到

(14)

把式(14)代入式(7)可得到

(λ2-1-μυ2)[(λ2-2)λ2-
2υ2(μλ2-1)+υ4(μ-1)]=0

(15)

解式(15)得

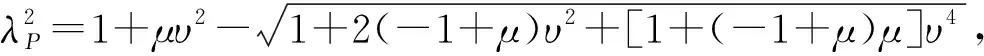
式(11)可以写成

(16a)

(16b)

第二步，把P点或R点与Q点的纵坐标调整到同一高度，联立式(16a)和式(16b)可以得到最优频率比为

(17)

将式(17)代入式(14)得到负刚度比

(18)

此时,

(19)

由于不恰当的负刚度值会使系统出现不稳定的现象，通过研究发现当预加荷载使系统产生位移等于固定点处响应值时，系统将处于稳定状态。为了验证式(18)的负刚度比，需令

(20)

即

(21)

其中,

从而得到

(22a)

(22b)

α3=2μ-2

(22c)

通过研究发现，只有α1能够在保证系统稳定状态下取得最优减振效果，其他结果不符合要求，因此选择α1作为最优负刚度比，即

(23)

(24a)

(24b)

根据固定点理论，无论阻尼比ξ如何选取，系统的幅频曲线都会通过P,Q,R三点，可知振幅最高点不会低于P,Q,R三点的纵坐标。最优阻尼比可以通过调整两个共振峰为同一高度时实现。从图3可知，当两个共振峰在同一高度时，Q点附近恰好是幅频曲线斜率为零的区域，即近似认为Q点的曲线斜率为零。根据极值条件，可知

(25)

联立式(25)可以得到近似最优阻尼比

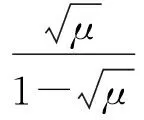
(26)

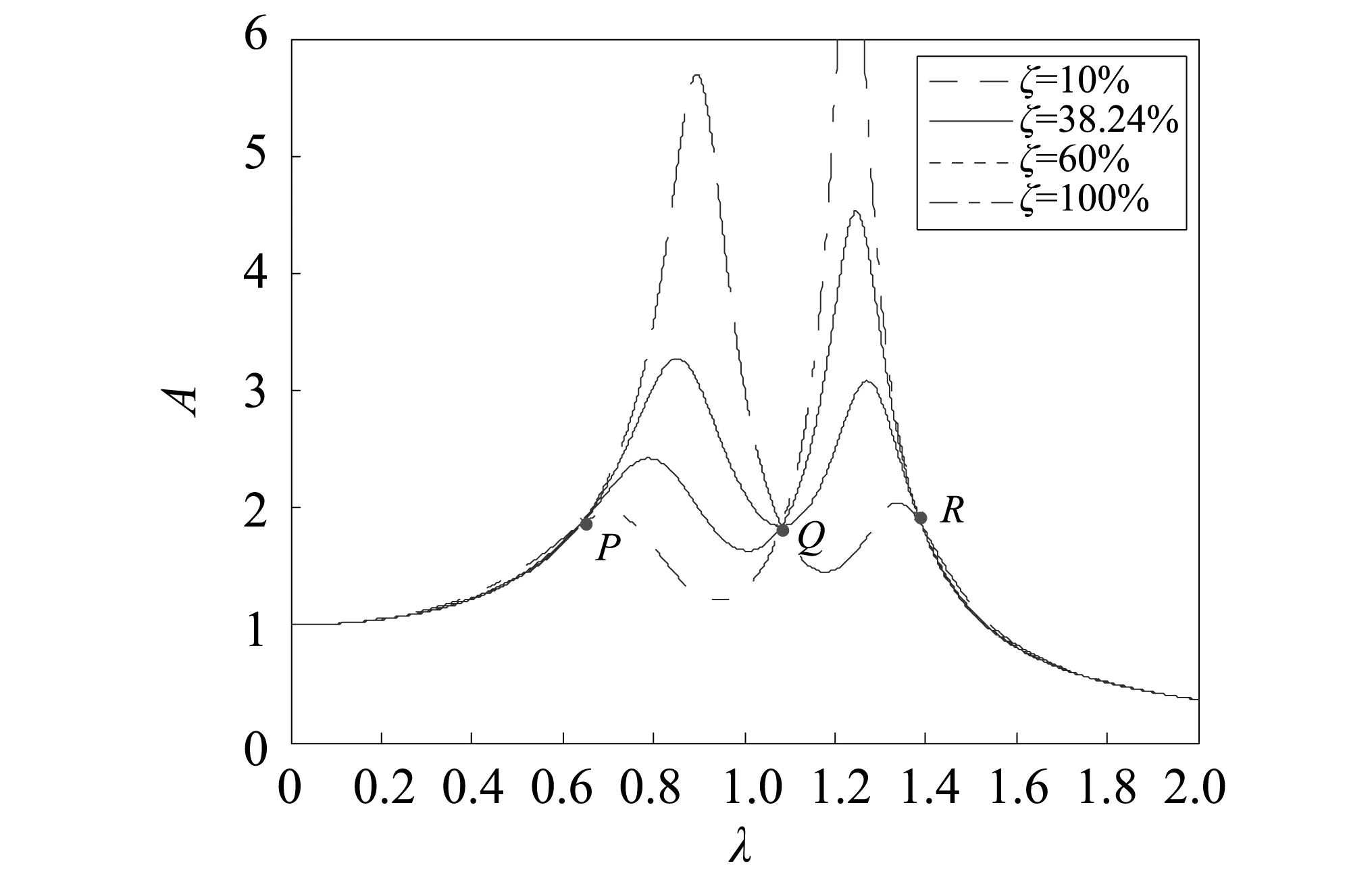
图3 不同阻尼比下幅频曲线Fig.3 The amplitude-frequency curve under different damping ratios

根据前述优化结果得到幅频曲线，如图4所示。可以发现基本实现了优化目标。从图3可知，当两个共振峰在同一高度时，Q点附近正好是幅频曲线斜率为零的区域，即近似认为Q点的曲线斜率为零，这是误差的来源之一。另外，选取最优负刚度比时，选取原则为“预加荷载使系统产生位移等于固定点处响应值”，这个过程也是近似的，是另一个误差来源，这两方面的原因导致了最终幅频曲线的不等高，但在可接受范围内。

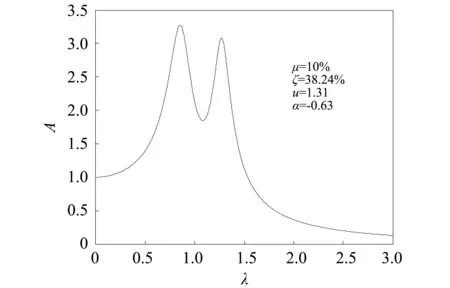
图4 化后的幅频曲线Fig.4 The amplitude-frequency curve

3 模型对比

为了证明该吸振器的减振效果，将本文提出的模型与三种传统的动力吸振器模型(即Den Hartog， Ren和Asami等的模型)优化结果进行了对比，其幅频曲线如图5所示。从图5可知，在相同质量比的情况下，本文提出的动力吸振器能够大幅降低系统共振区振幅，同时拓宽了减振频率。

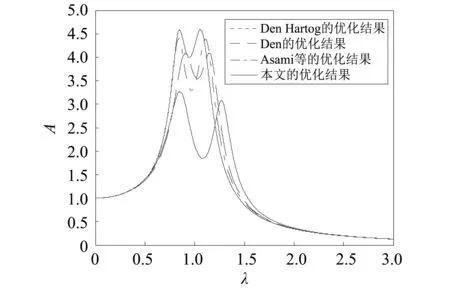
图5 μ=10%时与其它形式动力吸振器模型的对比Fig.5 The comparisons of the presented DVA with three other traditional DVAs when μ=10%

4 随机激励下响应对比

由于实际工程中，外激励的来源多为随机的或带有很强的随机性，因此，研究受随机激励的主系统响应很重要。设该系统受均值为零，功率谱密度为S(ω)=S0的白噪声激励，则本文模型与其它三种动力吸振器模型绝对位移响应的功率谱密度函数分别为

SM(ω)=|X1M|2S0,SV(ω)=|X1V|2S0
SR(ω)=|X1R|2S0,SA(ω)=|X1A|2S0

(27)

式中：下标M，V，R和A分别为本文模型、Voigt模型、Ren所提出的动力吸振器模型和Asami等所提出的动力吸振器模型。其中在Acar等的研究中已经给出Voigt模型和Ren所提出的动力吸振器模型的主系统位移均方值，于是四种动力吸振器模型的主系统位移均方值分别为

(28)

其中，

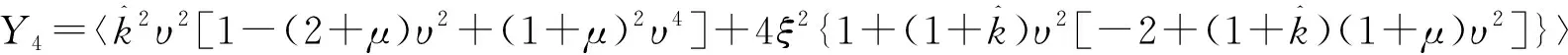
(29)

设四种动力吸振器模型中吸振器与主系统的质量比均取μ=10%，则根据本文优化结果以及现有文献的优化公式，可以得到均方值分别为

(30)

从结果对比可知，当主系统参数相同时，在随机激励条件下本文模型仍然具有较好的减振效果。

5 结 论

本文将负刚度器件引入到黏弹性材料中的Maxwell模型，并将含负刚度器件的Maxwell模型应用到动力吸振器中形成一种含负刚度器件的Maxwell模型动力吸振器。利用固定点理论和H∞优化准则对系统刚度和阻尼参数进行优化，同时在保证系统稳定性前提下得到了最优负刚度比。最后分别在简谐激励和随机激励条件下通过与其它经典动力吸振器模型的对比，证明了本文模型有较好的减振效果。