基于HJI理论的无轴承异步电机悬浮系统滑模鲁棒控制

孙宇新， 唐敬伟， 朱熀秋， 施 凯

(江苏大学 电气信息工程学院，江苏 镇江 212013)

无轴承异步电机通过在异步电机的定子槽中添加一套悬浮绕组，从而利用两套不同极对数的转矩绕组和悬浮绕组磁相互作用来改变电机气隙合成磁场的分布，进而在转子上产生可控径向力，实现转子的稳定悬浮和旋转，具有结构紧凑简单，无摩擦，弱磁容易，高速和超高速运行等优点，是特种传动应用领域最具有发展潜力的方案之一[1-2]。但是，由于悬浮绕组的加入，使得无轴承异步电机具有极其复杂的电磁关系，是一个多变量、非线性、强耦合的系统。对于无轴承异步电机而言，如果不能实现悬浮系统径向悬浮力之间非线性动态解耦控制，则不能保证电机转子稳定悬浮和可控旋转，进而无法发挥出无轴承异步电机优秀的性能。因此，实现对无轴承异步电机悬浮系统径向悬浮力之间动态解耦控制显得尤为重要，具有有重要的现实意义[3]。

自无轴承异步电机被提出以后，国内外学者对无轴承异步电机悬浮系统径向悬浮力之间动态解耦这一问题进行了研究并取得较多研究成果。文献[4]研究了基于气隙磁场定向矢量控制策略，实现了静态解耦但没有实现动态解耦，没有实现真正意义上的解耦控制。文献[5]采用了基于转子磁场定向矢量控制控制策略，实现了电磁转矩和悬浮力的解耦控制。但是采用PID(Proportion Intergration Differentiation) 控制策略，系统动态性能较差。文献[6-7]将逆系统方法应用到无轴承异步电机解耦控制当中，但是此方法严重依赖于电机的精确模型，而无轴承异步电机模型多建立于理想情况之下。因此，该方法很难在实际中应用。文献[8-9]采用神经逆系统实现了电机解耦控制，但是所构造的系统结构复杂，学习收敛速度较慢。文献[10]研究了自适应逆控制方法，该方法不需要辨别气隙磁链，取得了较好的效果。

滑模控制是一种特殊有效的非线性控制策略，具有响应快，抗扰动能力强、易于实现等优点，被广泛应用于对各种领域[11-14]。本文根据无轴承异步电机悬浮系统控制基本理论[15]以及滑模控制理论[16]，提出一种基于HJI(Hamiltom-Jacobi-Isaacs)理论无轴承异步电机悬浮系统滑模鲁棒控制方法，该方法在建立悬浮系统模型时，考虑了传统悬浮系统模型的不确定性以及外界扰动，同时通过设计合适的滑模控制律满足HJI不等式鲁棒条件来确保控制系统的稳定性，实现无轴承异步电机悬浮系统解耦控制并使系统具有更强的稳定性和抗扰动能力。仿真和试验结果证明了该方法的有效性，系统具有良好动静态性能和鲁棒性。

1 无轴承异步电机基本机理

1.1 无轴承异步电机悬浮基本机理

引入悬浮绕组后，电机原有旋转磁场平衡被打破了，使得电机气隙中一个区域里的磁场增强，其对称区域的磁场减弱，进而产生的麦克斯韦力合力指向磁场增强的方向。向转矩控制绕组通入电流I1产生磁链ψ1和向悬浮控制绕组中通入电流I2产生磁链ψ2，如图1所示。在忽略负载情况下，由于在气隙上侧ψ1和ψ2同向，合成磁密会增加；在气隙下侧ψ1和ψ2反向，则合成磁密会减少，从而磁拉力的分布发生改变，产生沿y正方向的径向悬浮力Fy。如果在悬浮控制绕组中通入反向电流，则可产生沿y负方向的径向悬浮力。同理，沿x轴方向的径向悬浮力Fx可以通过在悬浮控制绕组中通入与I2垂直的电流获得。

图1 径向悬浮力产生原理Fig.1 Generation principle of radial suspension force

1.2 无轴承异步电机悬浮力数学模型

无轴承异步电机有转矩绕组(极对数P1，电角频率ω1)和悬浮绕组(极对数P2，电角频率ω2)两套绕组。研究发现，当两套绕组满足P2=P1± 1，ω1=ω2时，径向悬浮力可以通过悬浮转子径向位移的负反馈来实现控制，从而实现转子稳定悬浮。

无轴承异步电机的径向悬浮力表达式为

(1)

式中：Fx，Fy为x，y方向的径向悬浮力；km=πp1p2Lm2/12rlμ0N1N2为电机结构常数；l为有效铁芯长度；μ0为真空磁导率；r为转子外径；Lm2为悬浮绕组的定转子间互感；N1，N2为转矩绕组和悬浮绕组的串联匝数；i2sd，i2sq为d，q轴向的磁悬浮力控制电流分量；p1，p2为转矩绕组和悬浮绕组极对数；Ψ1d,Ψ1q分别为转矩绕组气隙磁链在d,q轴上的磁链分量。

当转子处于偏心位置时，会导致无轴承电机气隙不均匀，从而造成气隙磁场不平衡产生偏心磁拉力，其表达式可写为以下形式

Fsx=ksx,Fsy=ksy

(2)

传统无轴承异步电机悬浮力建模时常忽略系统的不确定性以及外界扰动，多建立于理想情况之下[17]。本文建模时考虑到模型的不确定性以及外界干扰，根据动力学原理，将无轴承异步电机悬浮系统的运动方程表示为

(3)

式中：m为转子质量；Fsx，Fsy分别为转子偏心在x，y方向产生的固有麦克斯韦力。

无轴承异步电机悬浮系统常采用气隙磁场定向控制，有

ψ1d=ψ1,ψ1q=0

(4)

将式(4)代入式(1)中，则可表示为

(5)

2 转矩绕组气隙磁链辨识

由式(5)可知，无轴承异步电机悬浮力控制只与转矩绕组气隙磁链有关。根据无轴承异步电机数学模型，在静止等效α，β坐标系下，转矩绕组定子磁链可以表示为[18]

(6)

式中：ψ1sα,ψ1sβ为转矩系统定子磁链α，β轴分量；U1sα,U1sβ分别为定子电压在α,β轴方向分量；i1sα,i1sβ分别为定子电流在α,β轴方向分量；Rs1为转矩绕组的定子电阻。

转矩绕组气隙磁链在α,β坐标系中可表示为

(7)

式中：L1s为转矩绕组的定子漏感。

由式(7)可知，可通过采样电路采样电流电压信号在线辨识出转矩绕组气隙磁链值，从而实现无轴承异步电机径向悬浮力的控制。

3 滑模鲁棒控制系统

3.1 HJI不等式定理

在适当的正则性和带模有界条件假设下，完全可以通过一个扩展的HJI微分不等式是否存在正解来确定非线性不确定系统的鲁棒可稳定性[19]。

考虑如下模型

(8)

式中：d为外界扰动；z为系统的评判指标。

定义对于信号d，其L2指标为

(9)

为了评判系统的抗扰动能力，定义如下性能指标

(10)

式中：J为系统L2的增益，表示系统抗扰动鲁棒性能，且J越小表示系统的鲁棒性越强。

根据式(8)，HJI理论可描述为：对任意给定一个正数γ，如果存在一个正定且可微的函数L(x)≥ 0，并且[20]

(11)

则J<γ。

3.2 滑模鲁棒控制器设计

为了提高系统的稳定性，将HJI不等式应用于滑模鲁棒控制中，通过设计合适的滑模控制律，使式(11)条件满足，则J<γ，鲁棒条件成立，最终实现无轴承异步电机悬浮力解耦控制。

式(3)改写为向量形式，可表示为

(12)

假设理想位移指令为zd，则跟踪误差e=z-zd,结合式(12)和式(2)设计控制律为

(13)

将式(13)代入式(12)中，则可得

(14)

定义滑模函数并作为评价信号ζ，即

(15)

式中:c>0。

得

(16)

利用HJI不等式理论,可将式(16)改写为

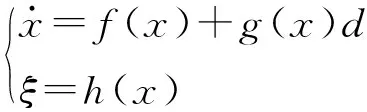
(17)

其中，

(18)

则，设计控制律为

(19)

定义Lyapunov函数为

(20)

则可得

(21)

定义

(22)

由式(21)和式(22)可得

(23)

由于

(24)

即H≤0,有

(25)

则根据HJI理论，可得J<γ，所设计的系统是稳定的。

3.3 无轴承异步电机控制系统设计

为了实现系统良好的动静态性能，本文提出了一种基于HJI不等式的无轴承异步电机悬浮力滑模鲁棒控制系统。同时，无轴承异步电机悬浮力控制只与转矩气隙磁链有关，则电机转矩绕组部分类似于一个普通的异步电机，对于转矩绕组部分的控制采用传统异步电机转速闭环矢量控制系统进行仿真研究[21]，无轴承异步电机控制系统，如图2所示，M=1/kmψ1。

4 系统仿真与试验

以一台无轴承异步电动机试验样机为研究对象。首先，在Matlab /Simulink中，建立本文所提控制系统仿真模型(见图2)。系统关键参数，如表1所示。滑模鲁棒控制器中γ=0.05。

图3为采用本文所提控制策略仿真结果波形图。电机启动给定转速为3 000 r/min，在0.3 s，转速由3 000 r/min突加至6 000 r/min。同时，转子x轴和y轴方向径向位移初始期望值都设置为0，在0.2 s，x轴方向径向位移值调整为0.2 mm，在0.4 s，y轴方向径向位移值调整为-0.2 mm。

由图3(a)可知。电机启动后，经过约0.05 s的调节时间，转速到达给定转速3 000 r/min后保持稳定，且超调量很小；当转速在0.3 s突加至6 000 r/min时，经过约0.05 s的调节时间，转子转速达到指定转速6 000 r/min，且超调量小，转速保持稳定。同时结合图3(b)和图3(c)分析，当转速在0.3 s突加至6 000 r/min时，x轴方向径向位移和y轴方向径向位移基本不受影响，仿真结果表明实现了转速和悬浮力之间的解耦。

由图3(b)和图3(c)可知，电机启动后，转子快速到达指定中心位置，并且保持稳定。在0.2 s，x轴方向径向位移值调整为0.2 mm时，转子能迅速响应，到达指定位置保持稳定，且超调量小。且此时电机转速和y轴方向径向位移基本不受影响。在0.4 s，y轴方向径向位移值调整为-0.2 mm时。转子也快速到达指定位置保持稳定。且此时电机转速和x轴方向径向位移也基本不受影响。仿真结果表明x轴方向径向位移发生改变时，y轴方向径向位移基本不受影响；y轴方向径向位移发生改变时，x轴方向径向位移也基本不受影响，实现了x轴方向径向位移和y轴方向径向位移之间解耦控制。

(a) 转速响应

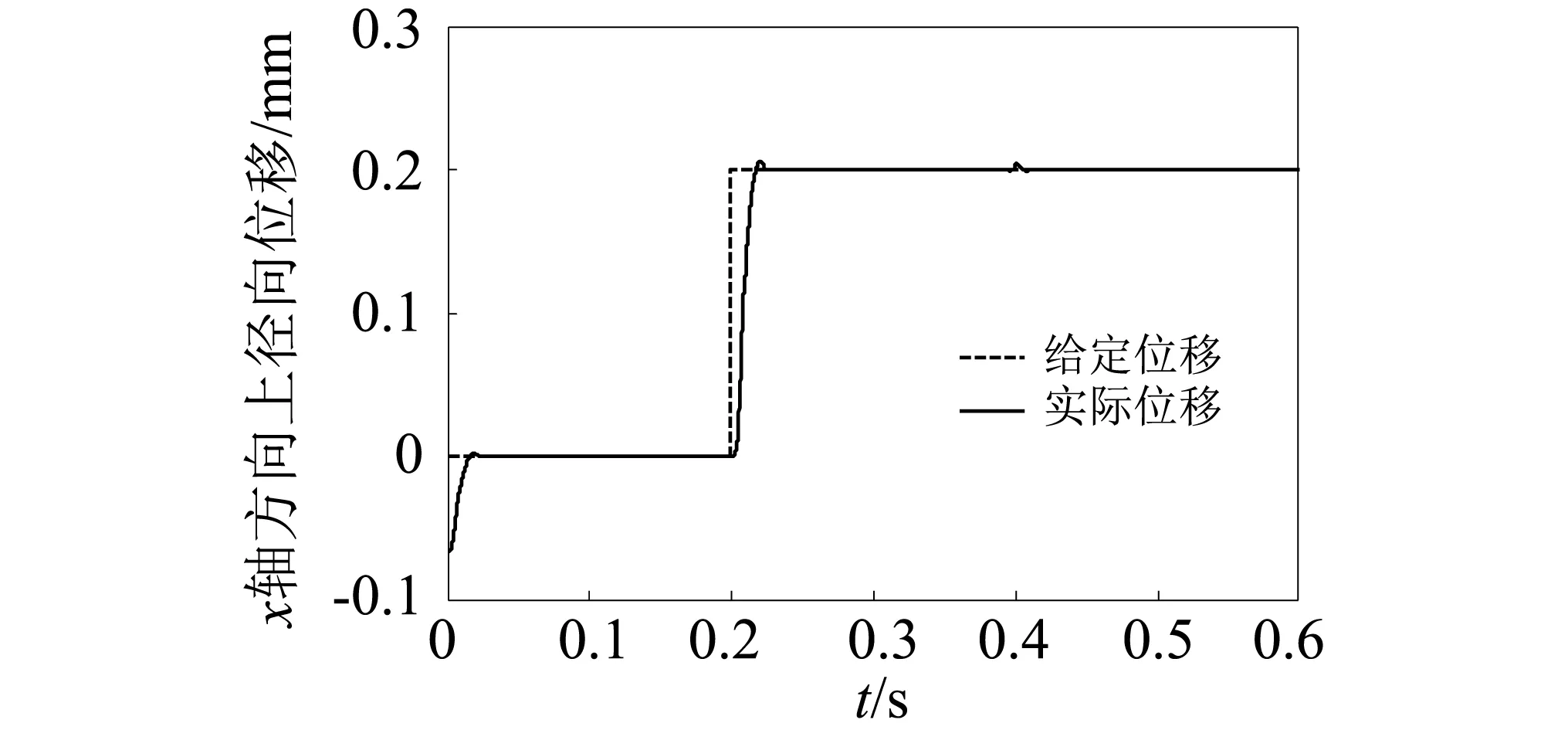
(b) x轴方向上径向位移

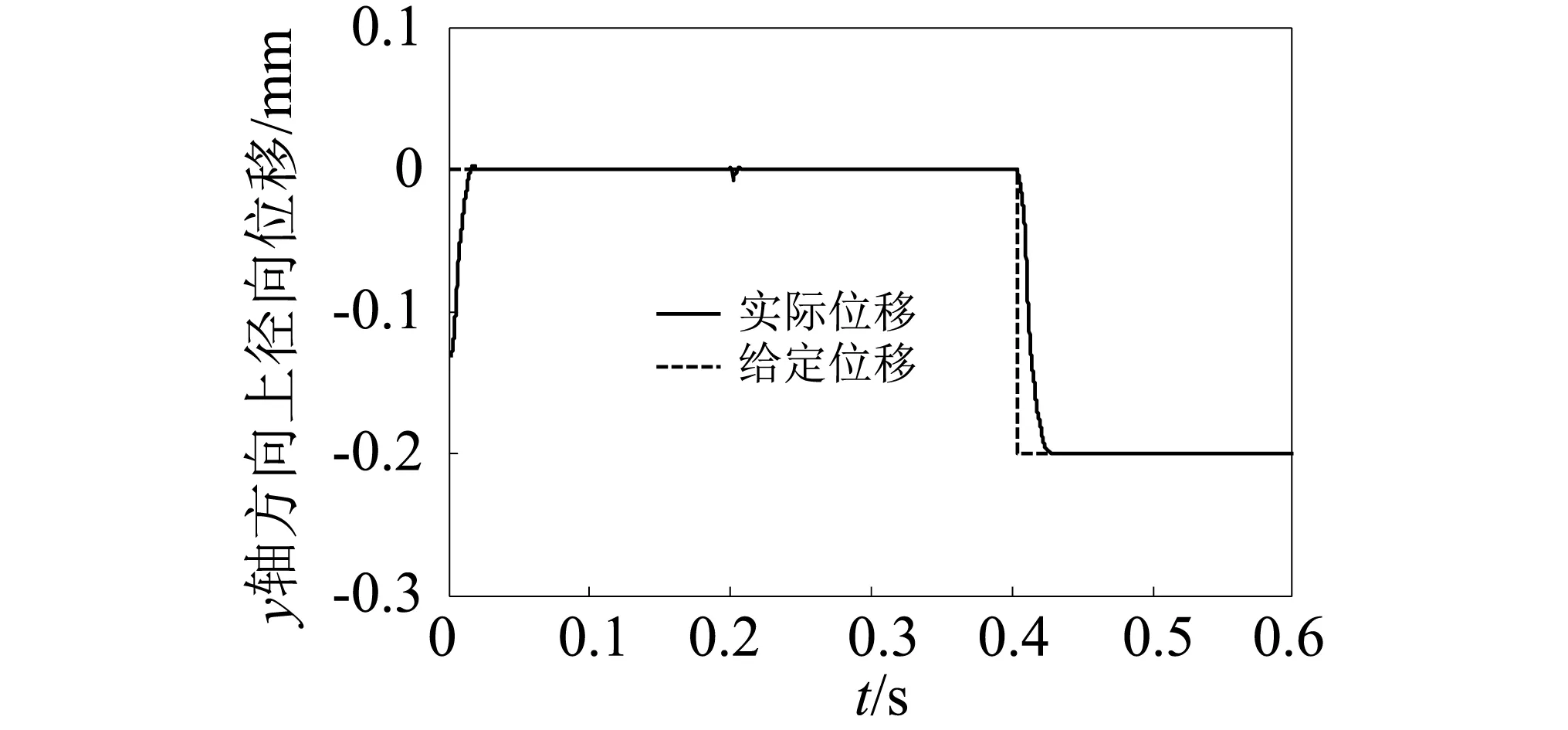
(c) y轴方向上径向位移图3 仿真结果Fig.3 Simulation results

图4为采用常规PID控制策略仿真结果波形图。同样，转子x轴和y轴方向径向位移初始期望值都设置为0，在0.2 s，x轴方向径向位移值调整为0.2 mm，在0.4 s，y轴方向径向位移值调整为-0.2 mm。

由图4(a)和图4(b)可知，电机启动后，转子也能到达指定位置，但调节时间和超调量比较大，最大超调量为0.2 mm，最长调节时间为0.6 s。同时，对比图3(b)、图3(c)和图4(a)、图4(b)可知，采用本文所提的控制策略，转子径向位移控制效果更好，调节时间更短，超调量更小。

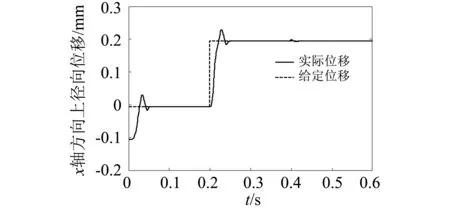
(a) x轴方向上径向位移

(b) y轴方向上径向位移图4 仿真结果Fig.4 Simulation results

为了进一步验证本文所提控制策略，利用无轴承异步电机试验控制平台进行试验验证。电机启动后，转子到达中心位置稳定后，转速给定由1 200 r/min上升为2 000 r/min时转子径向位移试验波形图，试验结果表明当转速变化时，转子径向位移基本不变，实现了转子转速与径向位移之间的解耦，电机转子能稳定悬浮，如图5所示。同时转子的径向位移同时误差小于±25 μm，充分证明所提方法的有效性。同时对比波形和试验波形可知，试验波形脉动较大，并且调节转速时，位移波形频率发生变化。分析该现象的原因，一方面是由于仿真建模时无轴承电机模型理想化，并且加工出来的电机转子质量分布不均匀，其它更深层次的原因则需要继续探究。

图6为电机转速到达800 r/min，在y轴径向位移方向突加扰动时转子径向位移试验波形图。由图6可知，当y轴径向位移方向突加扰动后，转子能在较短的时间回到稳定状态，表明系统具有很强的鲁棒性。此时，x轴方向径向位移基本不变。试验表明，所提控制方法实现了悬浮系统x轴方向径向位移和y方向径向位移之间动态解耦控制，同时系统具有很强的鲁棒性。

图5 y轴方向径向位移变化时转子径向位移试验波形Fig.5 The experimental waveform of radial displacement of rotor when displacement changes in y axis

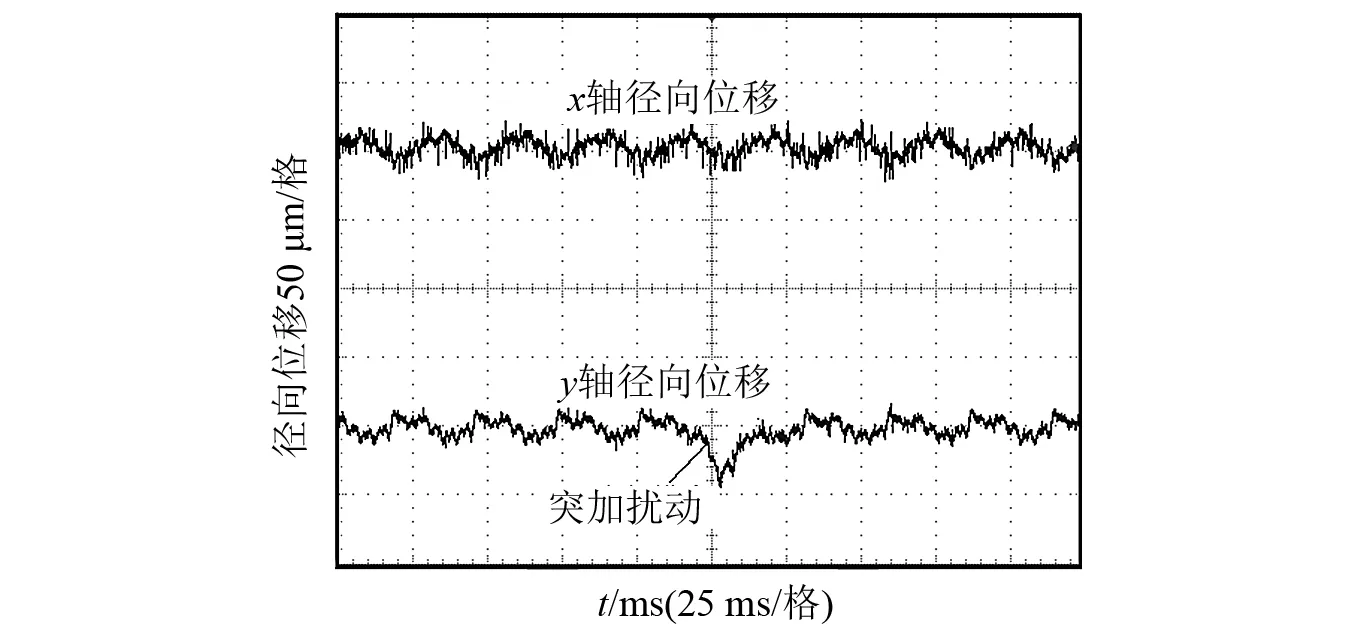
图6 y轴方向突加扰动时转子径向位移试验波形Fig. 6 The experimental waveform of radial displacement of rotor when sudden disturbance in y axis

5 结 论

针对无轴承异步电机悬浮系统解耦控制的需要以及传统悬浮力解耦控制中存在的缺陷，本文提出了基于HJI理论的无轴承异步电机悬浮系统滑模鲁棒控制系统。利用基于HJI理论的滑模鲁棒控制器代替传统PID控制器，与传统PID控制策略相比，该方法有效的调高了系统的控制性能，有效地降低了调节时间和超调量，并且系统具有很好的鲁棒性。仿真和试验结果表明该控制方法实现了无轴承异步电机悬浮力动态解耦控制，且系统具有较好的静态和动态性能，实现了无轴承异步电机转子的稳定悬浮。