MI3(M=Bi, Sb, As)弹性和电子性质的第一性原理研究

孙霄霄

(牡丹江师范学院物理与电子工程学院，牡丹江 157012)

1 引 言

第五主族元素M(Bi, Sb, As)和卤族元素碘(I)组成的二元化合物MI3在零温零压下是空间群为R-3的菱方结构，其中M原子与周围的6个I原子构成稍微扭曲的八面体结构。MI3是典型的层状结构材料，可以看作是片层沿C轴方向上交替堆垛而成，其中的每一层都是由I-M-I平面构成。近年来，随着微电子技术的发展，具有层状结构特征的金属碘化物，包括BiI3、SbI3和AsI3被广泛关注，可以用作卤素冶金、纳米材料、半导体、室温下γ射线探测器或X射线数字成像传感器的制作材料[1-4]，有着很好的研究价值和广阔的应用前景。但是目前金属碘化物工程化应用的主要瓶颈是难以生长出足够大尺寸的晶体和室温下晶体结构不稳定。最近，Lintereur研究团队成功生长出可以用作γ射线探测器的BiI3晶体[5]，实验上的成功激发继续深入探索此类材料的物理性质，为进一步的实验合成和理论研究提供指导。由于同主族元素存在相似的性质，所以对于同主族元素替换的二元化合物性质的研究非常重要。

早在1966年，Keller等[6]利用X射线衍射方法测量出BiI3的晶格参数，a=b=0.752 nm，c=2.072 nm。1996年，Molnár等[7]利用红外光谱实验和气相电子衍射方法对SbI3和BiI3的分子结构进行了研究。Saitoh等[8]在2000年通过拉曼散射实验测出在压强为1.66 GPa时，AsI3会发生结构相变。2002年，Virko等[9]利用密度函数方法和第一性原理方法计算了金属碘化物MI3(M=As, Sb, Bi)的分子结构和振动谱。2008年，Yorikawa等[10]利用Hartree-Fock近似对BiI3的电子性质进行了研究。2010年，Trotter研究了AsI3的晶格常数，a=b=0.721 nm,c=2.144 nm[11]。

目前，对MI3(M=Bi, Sb, As)这类化合物的力学性质和电子结构尚缺乏统一认识，所以有必要开展此方面的研究。本文利用基于密度泛函理论的第一性原理计算方法，在零温零压下对MI3(M=Bi, Sb, As)的结构、电子和弹性性质进行了系统的理论研究。

2 计算方法与晶体结构

2.1 计算方法

本文的计算均在基于密度泛函理论的第一性原理框架下采用CASTEP软件包完成[12]。其中电子和离子间相互作用采用超软赝势(USPP)，电子和电子之间的交换关联作用采取广义梯度近似(GGA)进行处理。外层价电子组态为：Bi的6s26p3，I的5s25p5，Sb的5s25p3，As的4s24p3，其余轨道电子视为芯电子。平面波截断能设置为300 eV。第一布里渊区k网格点的设置采用Monkhost-Pack方案，选取4×4×4以确保体系总能量能够很好的收敛。自洽(SCF)计算的收敛阈值设置为5.0×10-7eV/atom，体系总能量的收敛至5×10-6eV/atom，最大应力偏差保证低于0.02 GPa，每个原子上的最大受力低于0.1 eV/nm，原子的最大位移为5.0×10-5nm。采用Voigt-Reuss-Hill近似计算体模量、剪切模量、杨氏模量和泊松比。

2.2 晶体结构

图1 R-3相MI3(M=Bi, Sb, As)的晶胞结构模型，深色球和浅色球分别代表I和M原子 Fig.1 Crystal structure of MI3(M=Bi, Sb, As) with rhombohedral R-3 phase, the dark and light balls represent I and M atoms, respectively

为了找到MI3(M=Bi, Sb, As)在零压下的稳定结构，在之前的工作中对多种具有竞争力的AX3型晶体结构的焓进行计算，发现R-3结构的焓最低，是零压下的最稳定结构[1-2]。MI3(M=Bi, Sb, As)的晶体结构属于菱方结构，空间群为R-3，国际群号是148，每个晶胞中包含6个MI3分子式，晶体结构模型如图1所示，其中M表示金属原子，I表示碘原子。BiI3的晶格常数为a=b=0.752 nm，c=2.072 nm，α=β=90°，γ=120°[6]。Bi原子位于Wyckoff的6c (0.0000,0.0000, 0.1693)位置，I原子占据18f (0.3322,0.3146 ,0.0797)格点位置。SbI3的晶格常数为a=b=0.748 nm，c=2.090 nm，α=β=90°，γ=120°[13]。Sb原子占据Wyckoff的6c(0.0000, 0.0000, 0.1820)格点位置，I原子位于18f(0.3415, 0.3395, 0.0805)位置。AsI3的晶格常数为a=b=0.725 nm，c=2.155 nm，α=β=90°，γ=120°[14]。As原子位于6c (0.0000,0.0000, 0.1902)格点位置，I原子占据18f (0.3522, 0.3259, 0.0858)网格位置。

3 结果与讨论

3.1 几何结构优化结果

经过几何优化，计算得到的BiI3，SbI3和AsI3的平衡结构参数以及可用实验值列于表1。从表1可以看到，BiI3具有最大的体积和晶格参数。本文计算得到的理论值与实验值符合的很好，偏差在0.06%～4.2%之间，说明该计算方法和参数设置是合理的。

生成焓是指原子由单质合成化合物过程中所释放的能量，其关系式如下：

(1)

表1 MI3(M=Bi, Sb, As)的晶格常数a,b,c，单胞体积V0，生成焓ΔHTable 1 Calculated lattice parameters a, b and c, unit cell volume V0,enthalpy of formation ΔH for MI3(M=Bi, Sb, As)

3.2 弹性性质

材料的弹性性质常常与固体声子谱、状态方程、内部原子势等密切相关，对于分析材料的结构稳定性、硬度、化学键的性质、弹性各向异性特征、热力学性质等都具有很重要的作用。菱方晶体有6个独立的弹性常数C11，C12，C13，C33，C14和C44。计算得到的零压下MI3(M=Bi, Sb, As)的弹性常数如表2所列。

表2 计算得到的零压下MI3(M=Bi, Sb, As)的弹性常数Cij、体模量B、剪切模量G、B/G值、杨氏模量E、泊松比ν和德拜温度ΘDTable 2 Calculated elastic constants Cij, bulk modulus B，shear modulus G，B/G ratio，Young's modulus E, Poisson's ratio ν, and Debye temperature ΘD for MI3(M=Bi, Sb, As) at zero pressure

对于稳定结构，弹性常数Cij需要满足Born-Huang力学稳定准则[15]：

(2)

计算表明，BiI3，SbI3和AsI3在零压下均满足力学稳定标准，是力学稳定的，能够稳定存在。利用弹性常数，根据Voigt-Reuss-Hill (VRH)近似[16]可以计算材料的弹性模量，公式如下：

9BV=(C11+C22+C33)+2(C12+C23+C31)

(3)

15GV=(C11+C22+C33)-2(C12+C23+C31)+3(C44+C55+C66)

(4)

1/BR=(S11+S22+S33)+2(S12+S23+S31)

(5)

15/GR=4(S11+S22+S33)-4(S12+S23+S31)+3(S44+S55+S66)

(6)

其中，Sij=1/Cij。BV和GV分别是Voigt近似下的体模量和剪切模量，BR和GR分别是Reuss近似下的体模量和剪切模量。根据Hill平均可以进一步估算材料的剪切模量G、体模量B、杨氏模量E和泊松比ν，即

G=(GR+GV)/2,B=(BR+BV)/2

(7)

(8)

BiI3，SbI3和AsI3的体模量B、剪切模量G、杨氏模量E、泊松比ν的计算结果如表2所列。结果表明，这3种化合物的体模量、剪切模量、杨氏模量和泊松比的相对大小关系一致，依次为SbI3>BiI3>AsI3。体模量B是表征晶体对抗体积变化的物理量，剪切模量G能够表征材料抵抗塑性形变的能力。从表2可以看出，BiI3，SbI3和AsI3的体模量都较小，说明体系具有较强的可压缩性，其中AsI3抗体积变化的能力最弱，SbI3最强。较小的剪切模量意味着原子间存在较弱的方向性键。SbI3的剪切模量最大，这与它有较高的C44和C11有关，大的C44和C11有助于各向同性剪切模量的提高。SbI3原子间的方向性共价键是最强的，其次是BiI3，AsI3最弱。

B/G比值可以用来判断材料的延性(脆性)。根据Push经验，B/G=1.75是区分延性和脆性的临界值，B/G的值越大，固体越软，延性越好。计算得到SbI3的B/G=1.85，表明这个材料是延性材料。BiI3和AsI3的B/G值分别为1.70和1.45，都小于1.75，说明BiI3和AsI3是脆性材料。

泊松比ν能够反映晶体抵抗剪切的稳定性，也与材料的体积变化相关。ν值一般在-1～0.5之间，泊松比越大，说明材料弹性形变中体积变化越小，可塑性越好。从表2可以看到，这3种材料的泊松比都不大，说明材料在弹性形变过程中体积变化很大，在剪切上相对不稳定。另外，泊松比也提供了关于化学键结合性质的信息，对于原子间的结合力是中心力的固体，ν=0.25是下限值，ν=0.5是上限值，相当于具有无限大的弹性各向异性。所以，BiI3和SbI3原子间的力是中心力，而AsI3原子间是非中心力。

材料的弹性各向异性可能诱发材料产生微裂痕。因此，为了更好的了解材料的力学性质和提高材料的耐久性能，分析材料的弹性各向异性是十分重要的。所有已知的晶体都具有弹性各向异性特征，计算晶体的弹性各向异性在工程学上具有重要的含义。通过计算普适的弹性各向异性因子AU来分析晶体的各向异性特征，计算公式如下：

(9)

AU=0，代表弹性局部各向同性；AU值越大，代表单晶各向异性的程度越强。AsI3的AU=1.11, SbI3的AU=1.60，BiI3的AU=1.05，这3个值大大偏离零值，暗示了这三种材料大的弹性各向异性特征，其中SbI3的各向异性程度最大，AsI3的各向异性程度最小。

德拜温度是晶格最高振动简正模的温度，能够使材料的热力学性质和力学性质相关联，可以由下式计算得出：

(10)

其中，h是普朗克常数，k是玻耳兹曼常数，n为分子中原子的个数，NA为阿弗加德罗常数，ρ是密度，M是分子质量，Vm是平均弹性波速。Vl是纵的弹性波速，Vt是横的弹性波速。

(11)

(12)

计算结果表明(见表2)，德拜温度的大小关系依次为SbI3> BiI3> AsI3。

为了证明MI3(M=Bi, Sb, As)的压缩特性，计算了其相对体积V/V0随压强变化的关系，如图2所示。从图2中可知，这3种材料的相对体积都随压强的增大而减小，AsI3的相对体积减小的最多，说明高压下AsI3更容易被压缩。

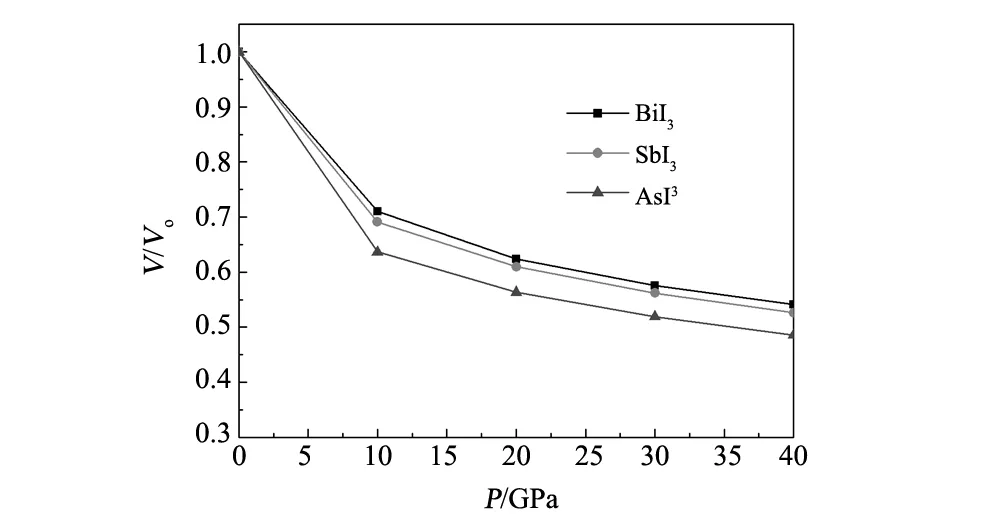
图2 V/V0随压强的变化关系 Fig.2 V/V0 as a function of pressure

3.3 电子结构性质

计算了0 GPa下BiI3，SbI3和AsI3沿布里渊区高对称点方向的能带结构，结果如图3所示。从图3可以看出，BiI3，SbI3和AsI3都是间接带隙半导体，BiI3的带隙为2.48 eV，SbI3的带隙为2.16 eV，AsI3的带隙为2.34 eV。BiI3，SbI3和AsI3的价带基本分为三个区域：位于-13～-11 eV，-10～-8 eV的下价带；-4～0 eV的上价带。导带位于2～4 eV和6～8 eV两个区域。这3种材料价带顶附近的能带的起伏不大，说明电子有效质量较大，电子的局域程度较强，色散较小。相邻轨道之间重叠不大，说明成键强度较弱。

MI3(M=Bi, Sb, As)的总态密度(TDOS)和各分波态密度(PDOS)如图4所示。从图4(a)可以看出，价带-13～-11 eV，-10～-8.5 eV能量区间的态密度主要由I-5s和Bi-6s电子贡献；-3.5～0 eV能量范围的态密度主要由I-5p，Bi-6p和少量Bi-6s贡献，I的5p和Bi的6s电子轨道发生杂化，形成共价键；在导带的2～4 eV能量范围，态密度主要由I-5p，Bi-6p和少量I-5s贡献；6～8 eV能量区间，态密度主要由I-5s和Bi-6s贡献。

图3 MI3(M=Bi, Sb, As)的能带结构图 (a)BiI3;(b)SbI3;(c)AsI3 Fig.3 Band structures of MI3(M=Bi, Sb, As) (a)BiI3;(b)SbI3;(c)AsI3

从图4(b)可以看出，价带中-13～-11.3 eV能量区间的态密度主要由I-5s决定，Sb-5s和Sb-5p贡献较少；-9.3～-7.5 eV能量区间的态密度主要由Sb-5s决定，I-5p的贡献较少；-4～0 eV能量区间，主要由I-5p，Sb-5p和少量Sb-5s贡献，I的5p和Sb的5s电子轨道发生杂化，形成弱共价键。在导带的2～3.8 eV能量范围，态密度主要由Sb-5p和I-5p贡献，I-5s贡献较少；5～7.6 eV能量范围，态密度主要由I-5s和Sb-5s贡献。

从图4(c)可以看出，价带中-13～-12.5 eV，-11.5～-11 eV能量区间态密度主要由I-5s和As-4s电子贡献；-9.5～-8.5 eV能量区间的态密度主要由As-4s决定，I-5p的贡献很少；-3.5～0 eV能量区间，主要由I-5p和As-4p贡献, As-4s贡献很少。在导带的2.5～3.5 eV区间，态密度主要由As-4p和I-5p贡献，As-4s贡献较少；6～8 eV能量区间，态密度主要由I-5s和少量的As-4s贡献。注意到I的5p和As的4s电子轨道发生杂化，形成共价键。

从图4(d)可以看出，这3种材料的电子态密度分布非常相似，总态密度在-11 eV、-4 eV、0 eV和4 eV附近显示出明显的峰特征，说明电子的局域程度较强。I-5s轨道远离费米能级，靠近费米能级以上的导带部分I-5p和M-p电子占主导地位。费米能级以下的价带，主要是I-p，M-p和M-s电子的贡献。费米能级处的总态密度曲线按SbI3、BiI3、AsI3顺序向低能级方向移动，且费米能级处的态密度值也相应降低，电子排斥作用增大，从而使材料的稳定性和硬度相应提高，这和力学性质的计算结果是一致的。Sb-I原子间的方向性共价键最强，As-I之间的共价键最弱。共价键的存在有助于材料对抗压缩，材料的强不可压缩性对应着大的块体模量值。共价键的强弱也能够反映体系热力学稳定性的程度，共价键越强体系的热力学稳定性就越高，因此，这三种化合物热力学稳定性的大小排序为SbI3、BiI3、AsI3，这已经在之前关于生成焓的计算中得到证实。

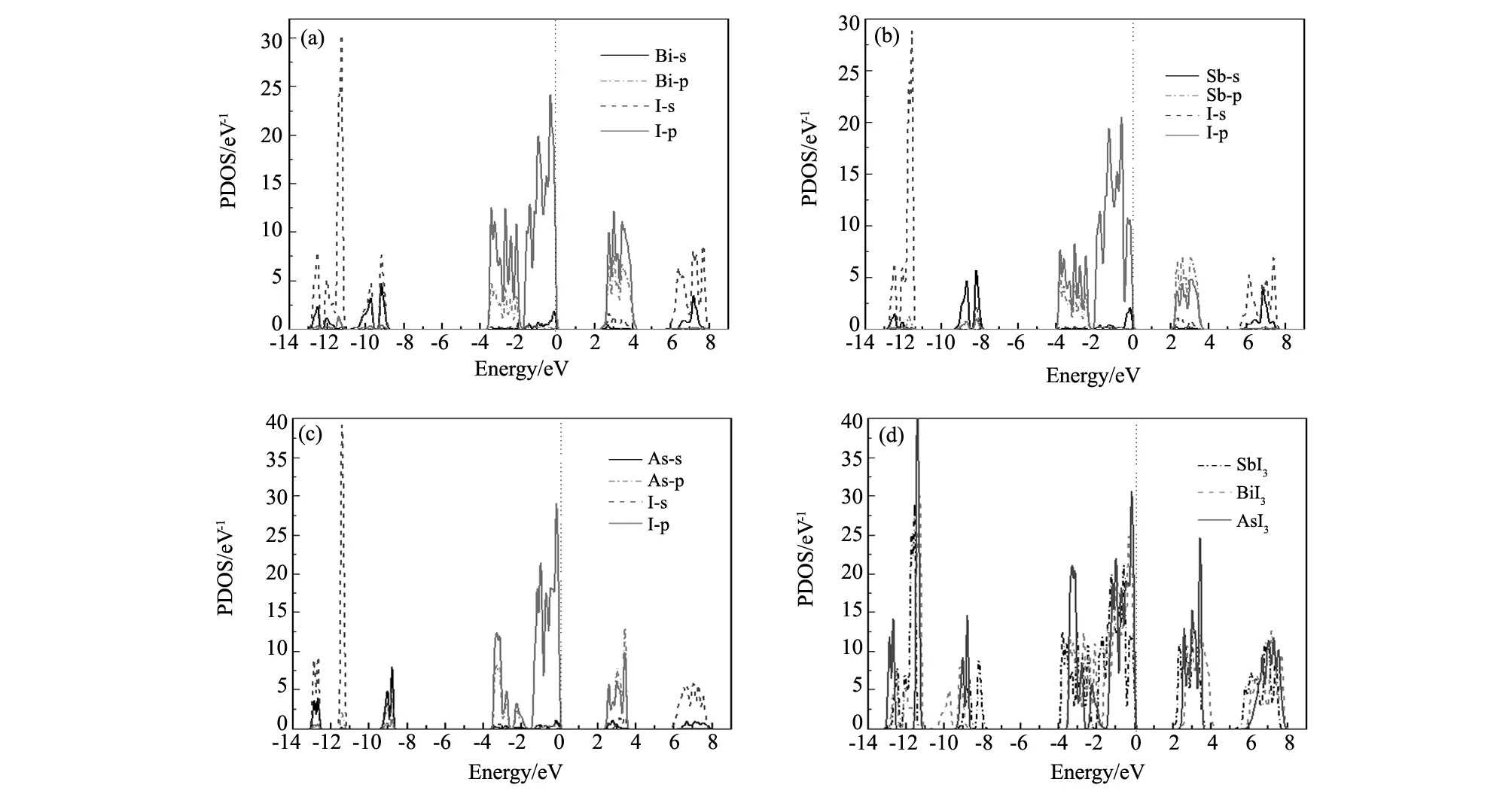
图4 MI3(M=Bi, Sb, As)的总态密度(TDOS)分波态密度(PDOS)图 (a)BiI3; (b)SbI3; (c)AsI3；(d)TDOS Fig.4 Total density of states (TDOS) and partial density of states (PDOS) of MI3(M=Bi, Sb, As) (a)BiI3;(b)SbI3;(c)AsI3;(d)TDOS

图5 MI3(M=Bi, Sb, As)的差分电荷密度图 (a) SbI3; (b) BiI3; (c) AsI3 Fig.5 Charge density distribution of MI3(M=Bi, Sb, As) (a) SbI3; (b) BiI3; (c) AsI3

为了解电荷分布和化学键的性质，实施了Mulliken原子布居数的分析，并在图5中画出MI3(M=Bi, Sb, As)的差分电荷密度图。从图5可以看出，电荷在金属M原子和I原子之间没有明显的积聚，原子周围电荷具有较弱的重叠，暗示M-I之间存在弱共价键，这与对态密度的分析结论一致。另外，从图5也可以观察到金属M原子周围电荷密度低于I原子，M原子和I原子之间存在电荷转移，I原子得到电子而金属M原子失去电子，这是典型的离子键特征。从Mulliken电子布居数的计算发现，BiI3中从Bi到I原子存在电荷转移(0.55 e),重叠布居数为0.10；SbI3中从Sb到I原子存在电荷转移(0.42 e)，重叠布居数为0.14；AsI3中从As到I原子存在电荷转移(0.24 e)，重叠布居数为0.06。M原子失去电子，I原子得到电子，原子间存在离子键，重叠布居数的值较小，说明键共价性较弱。综合分析表明，MI3(M=Bi, Sb, As)中的化学键是弱共价键和强离子键的混合。共价键可以对抗弹性、塑性形变，使材料具有较高的硬度，然而离子键的存在导致材料具有较小的剪切模量。

4 结 论

(1)SbI3、BiI3和AsI3在热力学上均是稳定的，能形成稳定的化合物，生成焓由小到大的排序为SbI3、BiI3、AsI3，说明SbI3比BiI3和AsI3更加稳定。

(2)通过对MI3(M=Bi, Sb, As)力学性质的分析可以得出，MI3(M=Bi, Sb, As)在零压下均满足力学稳定标准，是力学稳定的，能够稳定存在，且都具有弹性各向异性特征。SbI3是偏延性材料，BiI3和AsI3是脆性材料。SbI3、BiI3和AsI3具有较强的可压缩性，其中SbI3抗体积变化能力最强。高压下AsI3更容易被压缩。德拜温度的大小关系依次为SbI3>BiI3>AsI3。

(3)通过对MI3(M=Bi, Sb, As) 电子结构性质的分析发现，MI3(M=Bi, Sb, As)都是间接带隙半导体，电子的局域程度较强，色散较小。I-5s轨道远离费米能级，靠近费米能级以上的导带部分，I-p和M-p电子占主导地位，费米能级以下的价带，主要是I-p，M-p和M-s电子的贡献。在费米能级附近，I的p轨道电子和M的s轨道电子发生杂化，形成共价键。通过对差分电荷密度和Mulliken原子布居数的计算发现，化合物中存在离子键。从整体上看，MI3(M=Bi, Sb, As)中的化学键是弱共价键和强离子键的混合。