复合固体推进剂单向拉伸曲线的拟合分析*

2018-07-20李月常胡蒙莉张晓飞

固体火箭技术 2018年3期

刘领，李月常，胡蒙莉，张晓飞

(湖北航天化学技术研究所，襄阳 441003)

0 引言

复合固体推进剂是一种高固含量的高聚物复合材料，其力学模型为多变量的复杂函数[1-2]。虽然拉伸力学性能研究极其丰富[3-7]，但关注重点通常为抗拉强度与伸长率，而基于应力应变曲线的特性[8]以及确定初始模量或脱湿点的研究相对较少。

目前，通常采用的标准[9]规定拉伸初始直线段部分的斜率为初始模量，测定时曲线如有初始直线段则取3%～7%弦模量，如没有初始直线段则取0～5%割线模量。此外，还可采用1%～3%弦模量。但上述方法对曲线初始段的线性评判未作规定，实践中需依赖人工目测判断并选择取值区域。另外，生产中也采用自动模量，其计算方法为将曲线最大载荷的2%与最大载荷值之间均分为6区，然后分段线性拟合求取最大斜率。该方法虽便于自动取值，但单区域取值跨度过宽不利于线性拟合，且取值的区域不一定位于初始段，故不宜选择自动模量作为初始模量。

标准[10]规定曲线的脱湿形成阶段与发展阶段的分界点为脱湿点(或初始脱湿伸长率)，其值为斜率下降至初始模量85%的直线L与曲线的交点，依据曲线的不同形状采用不同的取值方法，如有初始直线段则直线L过曲线上伸长率为3%的点出发与曲线相交的另一点即为脱湿点，如没有初始直线段则直线L过原点出发与曲线相交得到脱湿点。同样，对曲线初始段的线性判断依赖人工。

此外，文献[11]针对双基推进剂特殊性，提出45°直线与曲线相切的点作为脱湿点(或屈服点)；文献[12]指出拉伸曲线初始直线段的切线与曲线上最大载荷处的切线的交点到曲线距离最短的点作为脱湿点(或标称最大应变值)；类似地，对曲线上初始点的切线与最大伸长率处的切线组成的夹角进行角平分处理，角平分线与曲线的交点也可作为脱湿点。但上述计算方法均基于曲线的作图法，由于引入了曲线本身外的自由度，脱湿点的位置会因曲线坐标系本身设置不同而变化。例如，当X轴保持不变而Y轴刻度间隔设置变大或者曲线纵向拉伸时，所得脱湿点会增大；反之，当曲线横向拉伸时，所得脱湿点则会减小。故上述作图法存在显著的非唯一性。

综上，对初始模量与脱湿点的计算目前存在多种选择方式，而无法实现唯一性，且未实现自动处理。本文采用Origin软件对复合固体推进剂单向拉伸曲线分析，确定了初始模量与脱湿点的计算方法，比较分析了多种函数模型的拟合效果，并进一步考察吸湿与拉速对丁羟推进剂(以下简称HTPB)与高能推进剂(以下简称NEPE)两类推进剂单向拉伸曲线特性的影响。

1 试验方法

采用Instron5567拉伸试验机，依照测试标准GJB770B方法413.1单向拉伸法。测试样品分别在干燥(放干燥剂的干燥器)与潮湿(装足量水的干燥器)环境储存7 d。试样装夹后，先预加不超过0.2 N的拉伸载荷，再进行位移与载荷清零开始试验。拟合数据区域为脱湿段，即起始点至最大伸长率εm，为避免初始拉伸时载荷采集的波动，起始点选择为伸长率0.7%。

2 典型推进剂拉伸曲线及其拟合效果

2.1 推进剂拉伸曲线及其拟合效果

图1为典型的HTPB单向拉伸曲线，采用Origin软件对曲线一阶求导，得到模量-应变曲线[13]，二阶求导得到模量变化率-应变曲线。

由图1可知，拉伸曲线初始段并非完全的直线段，故选用不同初始段计算模量会得到不同的模量值，而采用曲线拟合得到的原点切线斜率作为初始模量E0，则可避免初始段取值范围的不唯一性。

由模量-应变曲线进一步可知，模量初始时最大，然后逐步下降，在伸长率3%时出现平台期，之后持续下降。结合模量变化率-拉伸曲线可知，波谷处模量下降速度最大，可认为该点之前为脱湿形成阶段，模量下降速度越来越快；该点之后为脱湿发展阶段，模量下降速度逐渐变慢，直至近似匀速下降，故可将第一个波谷定义为初始脱湿点，求导可得εi=11.1%。

另外，曲线上总存在距过起始点与最大伸长率点的直线最远的点[13]，该点仅与曲线本身相关，不会随坐标系不同而变化，具备唯一性，固可定义该点为特征脱湿点εc，该点模量为特征模量Ec，Ec=σm/εm，其中σm为抗拉强度；通过平移相切法可得εc=14.9%。

图1 HTPB拉伸曲线及其一阶与二阶微分，拉速为100 mm/min(εm=0.416，σm=1.46 MPa)Fig.1 Stress-strain curve for HTPB propellant,first order differential and second order differential of curve, drawing speed was set to 100 mm/min (εm=0.416，σm=1.46 MPa)

拉伸曲线特点符合指数函数与多项式函数[14-15]，采用Origin软件编辑多种函数模型对推进剂拉伸曲线脱湿段进行拟合，效果如图2所示，拟合结果如表1所示。表1中，Z为Poly函数后续4次至9次等六项之和；括号内数值为已知量，与εm、σm相关。

可知式(2)对应的9次多项式函数(以下简称Poly)拟合效果最好，R2(即相关系数)为1，其他函数拟合的R2均达0.99以上。式(1)、式(2)、式(5)～式(8)中y0理论值为零，但由于拉伸初始采集波动，导致曲线初始点并非位于原点，进而拟合值不为零。

结合拉伸曲线自身特点：ε=0时，σ=0，σ′=E0；ε=εm时，σ=σm，σ′=0；进一步对式(1)～(8)中各参数与效果进行计算与讨论。结果如下：

式(1)中，a为E0，但拟合曲线尾部显著不满足特点Ⅱ；式(2)中，a为E0，且拟合曲线满足特点，R2达到1.000，拟合度最高；式(3)中，-a/b为E0，曲线拟合效果较好，但无法满足特点Ⅱ；式(4)中，a-b/c为E0，但拟合曲线尾部显著不满足特点Ⅱ；式(5)拟合曲线可反映拉伸曲线变化趋势，a为E0，b为εm，其中E0=eEc，e为自然常数；式(6)为式(5)引入σm、εm以及对ε进行修正的位移指数c所得，其中c拟合值接近1，拟合效果与式(5)相当，表明抗拉强度与伸长率的关系基本符合指数衰减形式σ=E0e-ε/εmε或σ=Ece1-ε/εmε。式(7)是在式(5)基础上引入位移系数c所构造的E0/Ec比值为某一变量的函数，式(7)R2为0.999，拟合效果较好，但参数意义不明。式(8)为式(7)以Ec代替a，εm代替b所得，其中E0=Ecc2/(e-c+c-1)。式(8)对曲线的初始段拟合效果较好，尾端拟合值略低。其中，c接近1，表明拟合效果与式(6)相当。

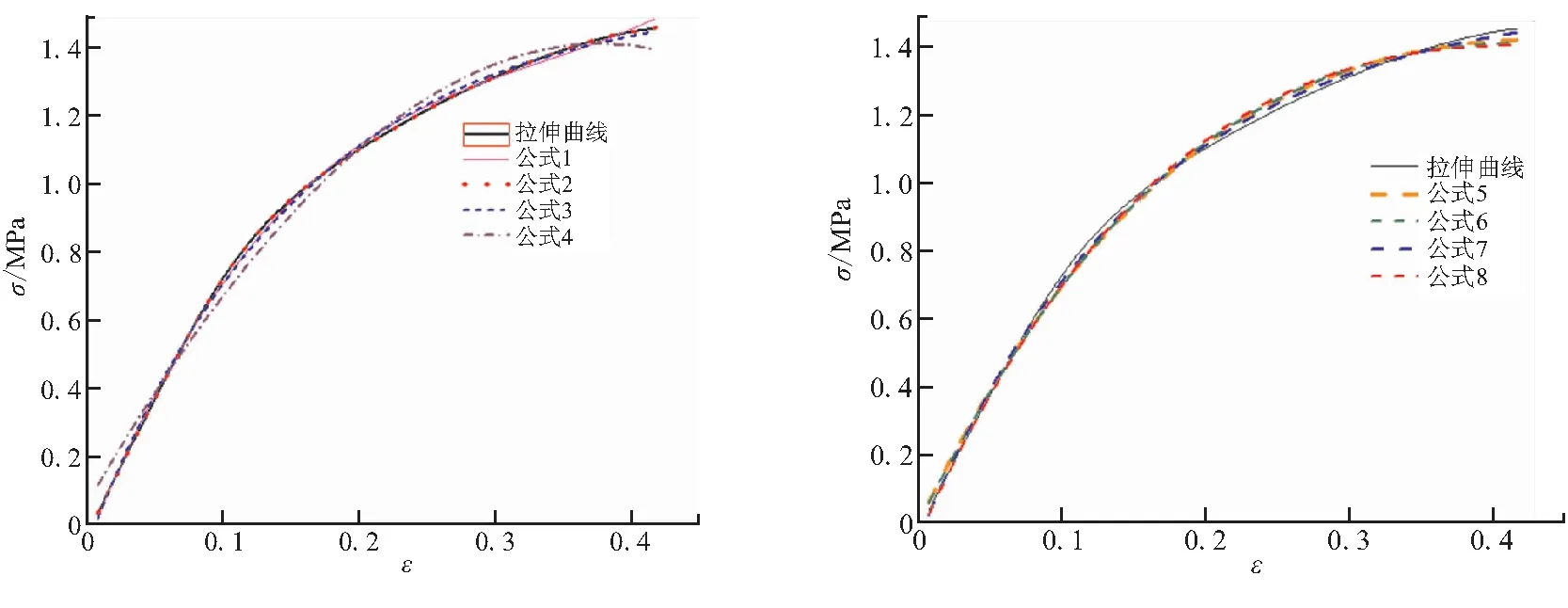
(a)式(1)～式(4) (b)式(5)～式(8)

表1 HTPB拉伸曲线采用不同函数模型拟合的结果(σ/MPa，ε/%)Table1 Results of various curve-fit methods to measure stress-strain curve for HTPB propellant (σ/MPa，ε/%)

综上所述，拉伸曲线脱湿段中抗拉强度随伸长率变化呈现较为明显的指数衰减关系，式(8)直接关联εm与σm，且各参数具有明确的物理意义，而通过Ec与位移系数c确定E0=9.4918 MPa，与式(2)中Poly拟合所得E0=9.287 MPa相当；反之，由E0与c，依据式(8)则可反推拉伸曲线的εm与σm。此外，c可反映式(8)相对于简单指数模型式(5)的偏离程度，其经验值有待进一步统计分析。

相比指数模型式(8)，Poly模型式(2)几乎完全匹配拉伸曲线脱湿段变化历程，具有更高的准确度。式(2)中一次项系数即为曲线原点斜率，故E0便于自动处理；另外，Poly拟合基于最小二乘法原理，可广泛用于各类拉伸曲线拟合。因此，采用Poly拟合计算E0具有较高的普适性与推广价值。

2.2 HTPB拉伸曲线拟合结果及讨论

采用Poly拟合不同条件下某典型HTPB拉伸曲线脱湿段，图3与图4分别为吸湿前后的拉伸曲线、模量-应变曲线与模量变化率-应变曲线，图5～图7分别为不同拉速条件下拉伸曲线、模量-应变曲线与模量变化率-应变曲线。其中，图3与图5中Poly拟合的R2均为1，表明Poly拟合与HTPB拉伸曲线完全吻合，能准确反映拉伸曲线。

图3 HTPB吸湿前后拉伸曲线及Poly拟合Fig.3 Stress-strain curves and polynomial fitting curves for HTPB propellant at different storage environments

图3中，吸湿前初始模量E0为9.287 MPa，吸湿后降至4.399 MPa。模量降低由于一方面水分累积在填料(如AP)表面形成低模量层取代了原有高模量层。另一方面，推进剂组分部分溶解或潮解，推进剂出现显著孔洞缺陷，使填料的补强作用失效[16]。

图4 HTPB吸湿前后模量-应变曲线与模量变化率-应变曲线Fig.4 First and second order differential of stress-strain curves for HTPB propellant at different storage environments

图5 不同拉速下HTPB拉伸曲线及Poly拟合Fig.5 Stress-strain curves and polynomial fitting curves for HTPB propellant at various drawing speed

由图4中模量-应变曲线可知，吸湿前样品在拉伸前期，模量先急剧下降，经过一段约5%的平台期后，再急剧下降；而吸湿后样品连续平滑下降。表明模量平台期与填料基体的键合强度相关，吸湿前由于存在高模量层，推进剂基体内微小孔洞向填料表面的扩展难以迅速发生[17]，进而与填料剥离的过程延迟，出现模量平台期。

图3中，吸湿前特征脱湿点εc为14.9%，吸湿后降至7.1%。图4中模量变化率-应变曲线可知，吸湿前存在波谷，对应有初始脱湿点εi为11.1%，而吸湿后无明显εi，曲线持续上升，表明拉伸初始时已发生脱湿。对比可知，吸湿前后εi与εc的变化趋势存在显著差异。

由图5可知，随拉速增加，最大伸长率εm呈递降趋势[18]，而E0从5.805 MPa增至14.205 MPa，且E0与拉速V的关系满足E0=1.694lnV+2.684，R2=0.918，该对数关系符合抗拉强度与拉速(或应变速率)对数的近似线性关系[5]。

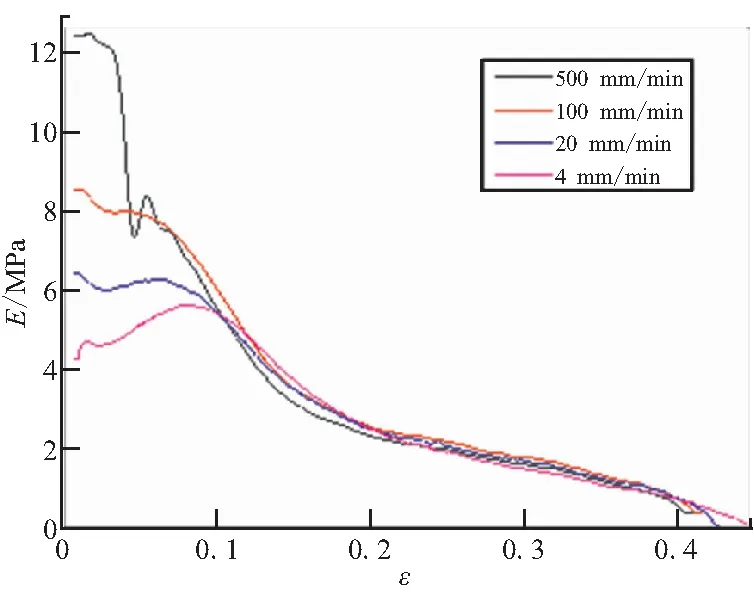
图6 不同拉速下HTPB模量-应变曲线Fig.6 First order differential of stress-strain curves for HTPB propellant at various drawing speed

同时，图5中随拉速增加，特征脱湿点εc从19.1%递降至14.0%；结合图7中随拉速增加，初始脱湿点εi由12.8%递降为4.1%。表明随拉速增加，εi与εc的变化趋势一致。

分析表明，对于该HTPB，拉速高时推进剂基体的构象变化来不及迅速发生。拉速越高，初始阶段应变越滞后于应力，故E0较高，进而使应力集中在填料与基体界面，导致εi或εc提前，εm较低；而拉速低时，利于基体孔洞的形成以及向填料表面的扩展[2，19]，拉速越低，基体孔洞向填料表面的扩展时间越充分，故E0较低，εm较高。

此外，由图6可知，以拉伸前期为例，随伸长率增加，500 mm/min拉速时模量下降幅度较大，而4 mm/min拉速时模量反而有上升趋势；不同拉速下各曲线模量拐点位于模量5～8 MPa之间，各曲线平台期结束后在伸长率10%附近产生交集，之后同等伸长率下模量基本相同。表明在模量平台期，填料高模量层周围已出现剥离，剥离至一定程度后，拉速对模量的影响较小。

2.3 NEPE拉伸曲线拟合结果及讨论

图8与图9分别为NEPE吸湿前后的拉伸曲线、模量-应变曲线与模量变化率-应变曲线，图10～图12分别为不同拉速条件下拉伸曲线、模量-应变曲线与模量变化率-应变曲线。其中，图8与图10中Poly拟合的R2均为1，表明Poly拟合能准确反映NEPE拉伸曲线。结合上文可知，Poly拟合通用于HTPB与NEPE。

由图8可知，NEPE吸湿前后，初始模量E0由4.241 MPa降至2.478 MPa，特征脱湿点εc从30.7%降至22.0%，与HTPB类同。

图8 NEPE吸湿前后拉伸曲线及Poly拟合Fig.8 Stress-strain curves and polynomial fitting curves for NEPE propellant at different storage environments

图9中，NEPE吸湿前后，模量-应变曲线显示均无模量平台期特征，模量变化率-应变曲线显示均无明显模量变化率波谷。结合上文可知，吸湿后两类推进剂均无模量平台期与模量变化率波谷；而吸湿前，HTPB存在模量平台期与模量变化率波谷，而NEPE均无。两类推进剂曲线存在差异。

由图9模量变化率-应变曲线可知，吸湿前NEPE拉伸前期，曲线先急剧上升后保持平稳，即模量下降速度迅速变慢后，模量再匀速下降。该变化趋势与HTPB差异显著，其原因为NEPE增塑剂含量高[2，20]，一方面，推进剂基体分子链段活动性强或柔顺性好而容易完成构象变化；另一方面，基体与填料的键合强度相对弱，故导致NEPE拉伸前期时，基体与填料即可能开始剥离，模量由最大值迅速下降，且下降的加速度越来越小，至模量拐点后，再缓慢匀速下降。

图9 NEPE吸湿前后模量-应变曲线与模量变化率-应变曲线Fig.9 First and second order differential of stress-strain curves for NEPE propellant at different storage environments

图10 不同拉速下NEPE拉伸曲线及Poly拟合Fig.10 Stress-strain curves and polynomial fitting curves for NEPE propellant at various drawing speed

由图10可知，随拉速增加初始模量E0从3.096 MPa递增至4.829 MPa，与拉速V呈对数关系模型E0=0.364lnV+2.550，R2=0.996。该趋势与HTPB一致。但随拉速增加，NEPE最大伸长率εm呈递增趋势[4]。对比图5可知，NEPE与HTPB的εm受拉速影响不同。

分析认为，相比HTPB，NEPE增塑剂含量高且基体柔顺性好，拉速高时基体的伸长率仍能较好发挥，故随拉速增加E0增大时，εm也增大。

图10还表明，随拉速增加特征脱湿点εc从26.5%递增至31.8%，与HTPB类同。结合图12中，各拉速下NEPE均无明显模量变化率波谷，初始脱湿点εi的位置只能作图近似取得，其中500 mm/min时，εi约为3.8%，其他拉速下2%。由于各条件下εi差距不大，且均接近于起始点，不具备明显差异，故不宜选取εi作为NEPE拉伸曲线脱湿点。而εc随拉速变化差异显著，故εc具备可比较的脱湿点特征，适用于NEPE脱湿点。结合上文可知，εi仅适用于HTPB，而εc通用于两类推进剂。

图11 不同拉速下NEPE模量-应变曲线Fig.11 First order differential of stress-strain curves for NEPE propellant at various drawing speed

图12 不同拉速下NEPE模量变化率-应变曲线Fig.12 Second order differential of stress-strain curves for NEPE propellant at various drawing speed

此外，由图11可知，不同拉速下模量随伸长率增加均呈现下降幅度先急后缓的特点，均在伸长率5%附近、模量2.5～3.5 MPa范围内出现模量拐点；其中，拉伸前期时，拉速越高模量下降幅度越大，且拐点越明显；模量拐点后，同等伸长率下低拉速时模量明显低于高拉速时[21]。这与上文HTPB模量变化趋势存在明显差异，其差异与二者拉伸过程中推进剂基体和填料的剥离过程相关。由于NEPE相比HTPB，基体柔顺性更好而基体填料的键合强度弱，一方面，NEPE拉伸前期时基体与填料即可能开始剥离，故模量曲线前期下降幅度先急后缓；另一方面，拉速越低时基体的伸长率越能较好发挥，故模量拐点后，同等伸长率下，拉速越低，模量越低。