聚酰亚胺复合膜的泊松比设计

刘朋博，张华振，徐 斌，侯仰青，兰 澜

(1.中国空间技术研究院西安分院，西安 710000；2.航天跃盛(杭州)信息技术有限公司 上海分公司，上海 201107)

0 引言

以薄膜结构为主体的天线[1-3]、太阳帆[4-5]、太阳能电池阵列[6]等受到越来越多研究人员的关注。聚酰亚胺(polyimide，PI)薄膜因其具有面密度低[7]，轻质和柔韧等特点，成为以上空间结构中首选的薄膜材料。在实际应用中，薄膜必须在张拉以后才能产生名为“应变刚度”的面外结构刚度。然而由于PI薄膜的泊松比较大(一般为0.35～0.4)，外力张拉薄膜会在膜面上的部分区域产生褶皱，影响膜面精度及稳定性，对结构的静态及动态特性产生耦合影响[8]。

为此，需要对薄膜的泊松比进行设计，从而削弱甚至消除薄膜的泊松比效应对膜面精度的影响。对于材料的泊松比设计，一般都集中在实现材料的负泊松比上，因为负泊松比可以让材料产生拉胀行为[9-10]。从20世纪80年代末开始，负泊松比材料成为材料领域的研究热点，而旋转刚性单元机制是这一领域被深入研究的主题之一[11-15]。该机制的本质是在材料上周期性地切割出某些形状的孔，以获得与孔间边界区域连接的刚性胞元，孔间边界区域模拟铰链，允许刚性胞元绕孔间边界区域“铰链”旋转，从而表现出效泊松比的现象。 Hou等[16]讨论了使用 Kevlar 机织织物/914 环氧预浸料和 Kirigami 技术制造的分级蜂窝结构的拉胀性。Bertoldi等[17]对由“Feguramed GmbH”制造而成的加成固化硅橡胶(sil AD spezial,SADS)进行圆形阵列研究时发现,单轴压缩的屈曲结果会产生椭圆孔阵列。他们进一步分析了孔隙率对等效泊松比的影响。Taylor等[18]对6061铝合金结构使用正交椭圆孔阵列，从实验和仿真两个方面分析了孔隙率对结构等效泊松比的影响。Pozniak等[19]研究了当在正交的椭圆孔中填充带有取向的夹杂物时，材料的等效泊松比和杨氏模量变化规律。Bonfanti等[20]对正交椭圆孔阵列的薄膜在张拉中产生褶皱的半波长和幅值等参数随等效泊松比的变化规律进行了研究。

Xu等[21]则将具有正交椭圆孔阵列的材料应用到碳纤维增强硅胶制造的空间可重构反射面上，通过优化设计椭圆孔的几何参数实现反射面的变泊松比，保证了型面精度。

本文针对一种应用于空间天线结构的正交各向异性的同质纤维增强聚酰亚胺复合膜，采用正交椭圆孔阵列的泊松比设计方式，通过基于COMSOL Multiphysics的有限元分析，探究4种不同纤维分布密度的复合膜在不同的胞元孔间边界距离下经纬双向的泊松比随椭圆纵横比的变化规律。

1 研究方法

1.1 材料及其力学性能参数

复合膜的基质薄膜的杨氏模量为3.245 45 GPa，泊松比为0.373 72。增强所用聚酰亚胺纤维的单丝直径为11 μm，断裂强度3.70 GPa，初始模量121 GPa，断裂伸长率3.24%，50根丝构成一束。复合膜的示意图如图1所示。

图1 复合膜的示意图Fig.1 Schematic diagram of a piece of composite film

本课题选用了3种不同经向纤维密度n的复合膜，它们分别是5束/cm，10束/cm， 20束/cm。本课题对纯薄膜进行了同样的仿真分析作为对照。在进行泊松比设计前，根据有限元分析和实验测量的结果(采用ANSYS Workbench 19.0软件进行有限元方法的模拟。得到其杨氏模量和泊松比。并采用INSTRON 68TM-30拉伸机配合双向测试的2663-901 AVE2非接触式双向引伸计进行测定对有限元方法加以验证。)，4种薄膜未打孔时的力学性能参数如表1所列。

表1 未打孔时薄膜的力学性能参数

1.2 正交椭圆孔的几何参数

针对上述的4种薄膜，截取30 mm×30 mm的区域作为胞元，进行正交椭圆孔的打孔设计。打孔后的胞元如图2所示。胞元的边长d=30 mm，打孔椭圆的横半轴长为a，纵半轴长为b，孔间边界距离为g。

图2 复合膜的打孔方案Fig.2 Perforation scheme of a piece of composite film

正交椭圆孔阵列的打孔设计方案实现泊松比调整的原理如图3所示，当在一个方向对胞元施加位移时，胞元将发生旋转，导致在与其垂直的方向上产生正向位移，引起胞元的等效泊松比发生变化。等效泊松比的计算方法如式(1)所示：

(1)

式(1)中μeff为等效泊松比，εy为y方向应变，εx为x方向应变，其余符号的含义如图3所示。

图3 泊松比变化的原理Fig.3 The schematic of Poisson’s ratio change

如图3所示，对于正交椭圆孔阵列的研究，在几何数据上，既有将对泊松比影响因素分为胞元的孔间边界距离g和椭圆纵横比2a/2b的，也有将对泊松比的影响因素分为孔隙率和椭圆纵横比2a/2b的。首先对于胞元的孔间边界距离g和椭圆纵横比2a/2b，两者是独立的，而孔隙率是一个既和胞元的孔间边界距离g有关，又和椭圆的纵横比a/b有关的参数。孔隙率与孔间边界距离g和椭圆纵横比2a/2b的关系可以由式(2)所示：

(2)

由式(2)可以看出，孔隙率φ不是一个独立的参数。

另外，虽然胞元的孔间边界距离g和椭圆纵横比2a/2b是独立的，但椭圆纵横比是一个没有上限的参数，甚至可以达到无穷大。固定g值，当椭圆很扁的时候，长短轴的长度稍微变化，椭圆的纵横比就会有非常大的变化，很难从胞元的等效泊松比和椭圆纵横比2a/2b的关系中总结出规律。而此时(a+b)是一个固定值。

本文考虑的泊松比影响因素分为胞元的孔间边界距离g和椭圆长半轴长度a与椭圆长短半轴之和(a+b)的比率，即r=a/(a+b)。这样不但保证了两个参数之间的独立，同时又保证了两个参数的值都在一个被限定的范围内，当g=3.0 mm时，r=a/(a+b)与椭圆纵横比2a/2b的关系如图4所示。

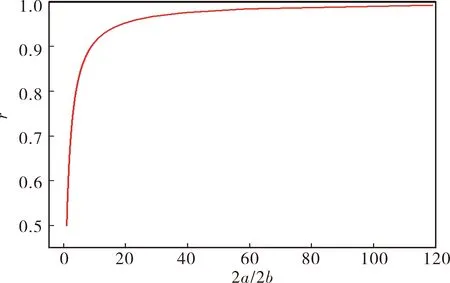
图4 椭圆纵横比与r之间的关系Fig.4 Relationship between ellipse aspect ratio and r

1.3 有限元分析

对于选中的4种薄膜，选取不同的薄膜孔间边界距离进行设计，即g=1.5 mm，g=3 mm，g=4.5 mm，g=6 mm，g=7.5 mm和g=9 mm，6种g值，此时g分别占胞元边长d的5%、10%、15%、20%、25%、30%。在此基础上，通过改变椭圆的纵横比，分析椭圆从r=a/(a+b)=0.5(a/b=1，圆形)演化到r=a/(a+b)=0.98(a/b=49，纵横比极大的椭圆)的过程中，薄膜胞元的泊松比的变化规律。

采用COMSOL Multiphysics 5.4有限元分析软件对上述薄膜进行建模和有限元分析，采用壳单元对复合膜进行建模，因为纤维对复合膜的泊松比影响主要体现在正交各向异性的纬向泊松比上，所以等效方法对泊松比设计是可行的。将厚度设置为110 μm，为符合壳单元的基本假设，网格大小应该大于厚度值。如图5所示，设置最大的单元长度为1.65 mm，最小的单元长度为1 mm，符合应用壳单元的假设。根据图3所示加载和约束方法对胞元进行约束。

图5 薄膜的网格划分Fig.5 Meshing of a unit

2 结果与讨论

2.1 薄膜的经向泊松比变化规律

4种薄膜的经向泊松比μ12变化规律如图6所示。可以看出，4种膜的经向泊松比在所有g值下随着r值的增大而减小，且均服从①缓慢减小；②减小趋势加剧；③逐渐趋于稳定。当g值较小(g=1.5 mm，g=3.0 mm)时，①过程不明显，泊松比的变化主要体现为②+③过程。随着g值的增大(g=4.5 mm，g=6.0 mm)，可以清晰地看出，随着r值的变大，①、②、③过程顺序出现。当g值超过胞元边长d的25%时(g=7.5 mm，g=9.0 mm)，③过程不再明显，经向泊松比的变化主要由①+②过程组成。

4种薄膜在r=0.5时经向等效泊松比μ12均为正值，此时的薄膜胞元不发生旋转，等效泊松比大小主要与g值有关，g值越大，残余的泊松压缩效果越大，经向等效泊松比μ12越大。以纯薄膜为例，g=1.5 mm，g=3 mm，g=4.5 mm，g=6 mm，g=7.5 mm和g=9 mm对应的经向等效泊松比μ12分别为0.11，0.17，0.23，0.26，0.29，0.31。可以看出，当薄膜胞元不发生旋转时，g值的增大对经向等效泊松比μ12的增大效果随着g值增大逐渐减弱。而随着椭圆的纵横比逐渐变大，可以看出，g=1.5 mm宽度的薄膜经向等效泊松比μ12很快达到-1，然后稳定在-1左右。而随着g值的变大，r值变大得到的泊松比逐渐变大，也即薄膜胞元的旋转效应逐渐变得不明显。以纯薄膜为例，当g=3 mm，g=4.5 mm，g=6 mm，g=7.5 mm和g=9 mm，5种g值时，经向等效泊松比μ12最小(r=0.98)分别只能来到-0.95，-0.83，-0.64，-0.39，-0.15左右。g值的增加带来旋转效应的减弱，而且减弱的程度随g值的增加有所提高。综合二者可以看出，g值对r=0.5和r=0.98下的影响虽然都是使得等效泊松比随g值变大，但g值的影响程度相反，前者小g值下g的变化影响大，后者则是大g值下的g值变化影响大。

图6 经向泊松比μ12变化规律Fig.6 Variations of warp direction Poisson’s ratios μ12

2.2 薄膜的纬向泊松比变化规律

4种薄膜的纬向泊松比μ21变化规律如图7所示。可以看出，纬向泊松比μ21随r值的演化过程与经向泊松比μ12类似，均可以分解为①缓慢减小；②减小趋势加剧；③逐渐趋于稳定，3个过程。值得注意的是，纯薄膜的经纬双向泊松比数值一致，这是因为纯薄膜是各向同性的。与同种有纤维薄膜的经向泊松比μ12相比，纬向泊松比的下降趋势更缓慢，而且这种缓慢趋势随着薄膜的经向纤维密度增大更加明显。纯薄膜、5束/cm的复合膜、10束/cm的复合膜、20束/cm的复合膜在g=1.5 mm时纬向泊松比μ21下降到-0.9左右时对应的r值分别是0.66，0.68，0.7和0.74。而当r=0.5，g=1.5 mm时，纯薄膜、5束/cm的复合膜、10束/cm的复合膜、20束/cm的复合膜的纬向泊松比μ21分别为0.109，0.078，0.064和0.048。纬向泊松比μ21下降的量变小，而要求的椭圆纵横比却增加。在其他g值下也有类似的规律。这一规律可以总结为：随着经向纤维密度的增加，在同一个g值下的薄膜纬向泊松比μ21下降变得困难。

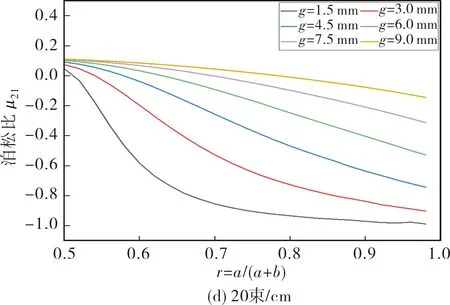
图7 纬向泊松比μ21变化规律Fig.7 Variations of weft direction Poisson’s ratio μ21

2.3 等效泊松比的影响因素

通过上述内容可以看出，打孔后的泊松比随g值变大而变大，随r值增大而减小。实际上，对同一材料而言，打孔后等效泊松比主要由两个因素支配，即打孔后孔间边界距离g，椭圆长半轴a与长短半轴长度之和(a+b)的比例r。g值决定了材料参数对打孔后胞元的泊松比影响程度，同时影响胞元的旋转能力，固定r，g值越大，旋转能力越弱，同时材料本身性能参数的影响越大，等效泊松比也越大。r值则影响了胞元的旋转能力，固定g，r值越大，旋转能力越强，打孔后的胞元等效泊松比越小。

如图8所示，当这两种薄膜胞元的材料参数相同，r=0.98时，两种薄膜等效泊松比只和g值有关。当g值分别等于1.5 mm和9.0 mm时(图8(a)和图8(b))，首先泊松压缩的残留效果不同，前者弱于后者；其次，胞元在旋转时，绕着孔间边界区域旋转，宽度越宽，相当于对胞元的约束程度越大，越不利于胞元的旋转。所以图8 (a)中的等效泊松比μa,eff小于图8 (b)中的等效泊松比μb,eff。

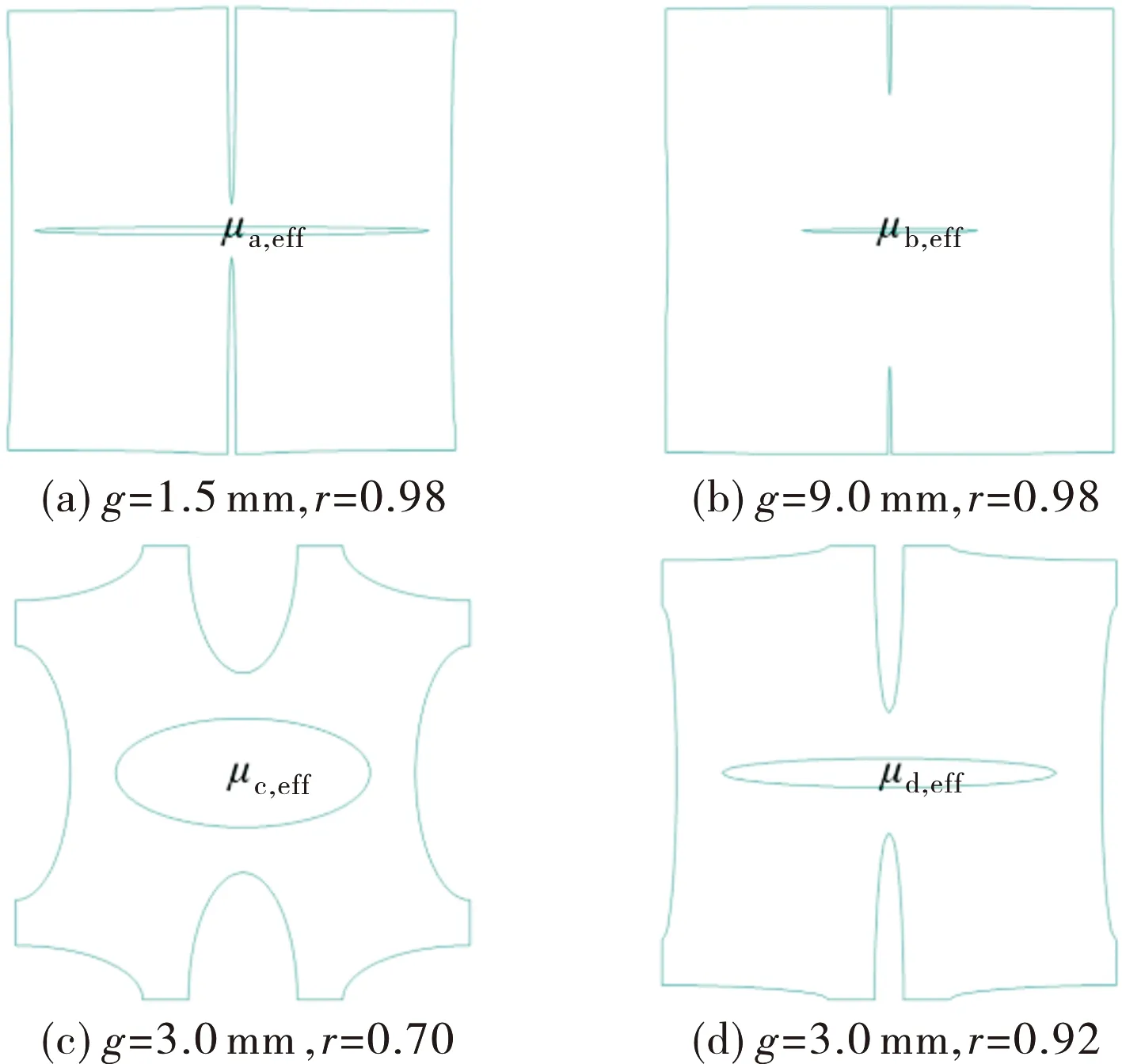
图8 参数对薄膜胞元泊松比的影响Fig.8 Influences of parameters on Poisson’s ratio of a membrane unit

如图8 (c)和图8 (d)所示，如果两种薄膜胞元的材料参数相同，g=3.0 mm，当r=0.7和0.92时，薄膜胞元的旋转能力明显不同。当胞元受到一个方向的拉伸载荷时，胞元中心的椭圆孔趋向于变成一个圆形，即被“拉开”，当椭圆的纵横比较小时，椭圆很容易达到“拉开”的上限，如图9(a)所示。而当椭圆的纵横比较大时，椭圆被“拉开”后的形状较之未“拉开”时变化较大，所以带来的胞元旋转能力也较大，如图9(b)所示。图8(c)中的等效泊松比μc,eff大于图8(d)中的等效泊松比μd,eff。

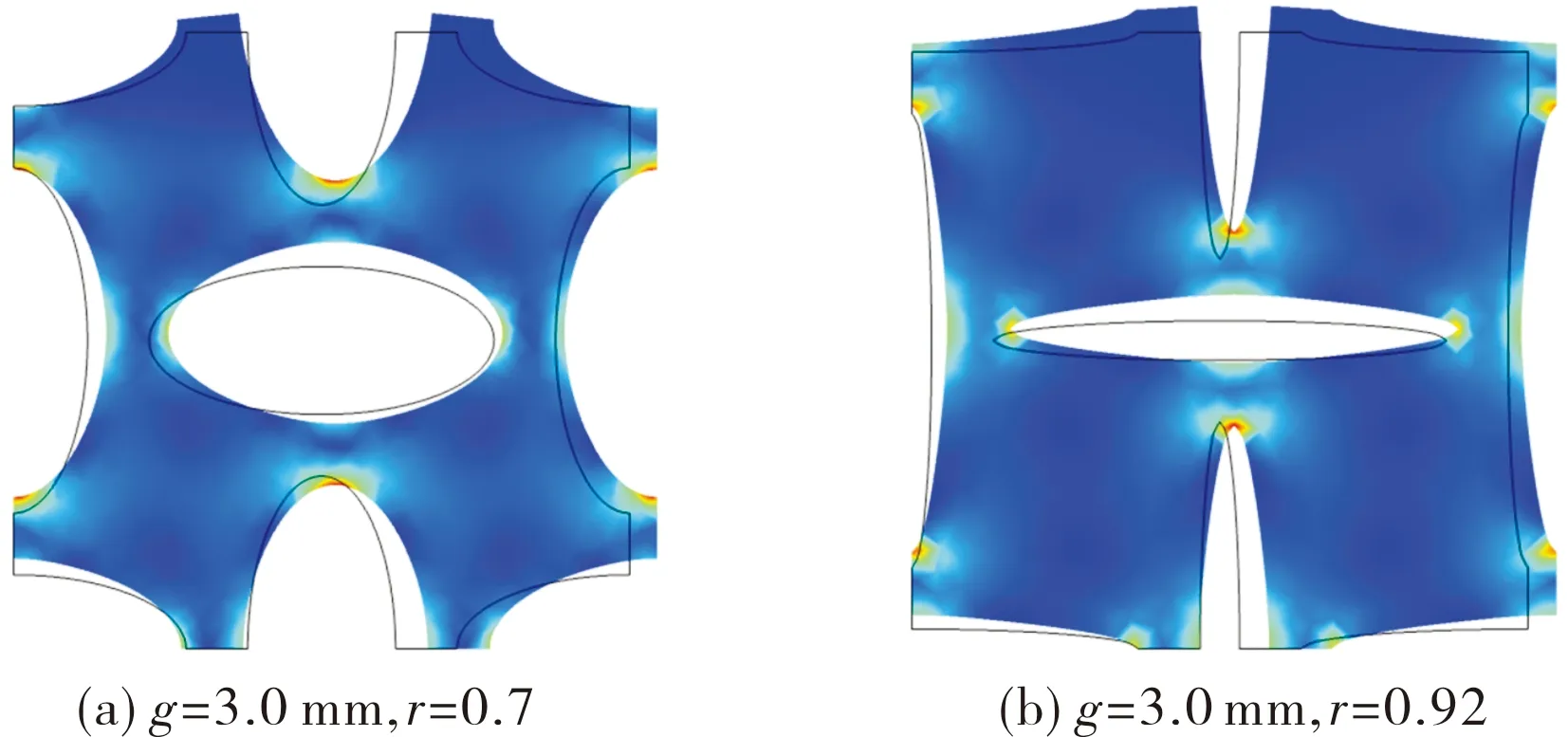
图9 不同r下薄膜胞元的变形前后对比Fig.9 Comparison of film unit deformations with different r

值得一提的是，泊松比的调整效果与外载荷的大小无关。在实际工程应用中，任意外载均可实现文中所提到的泊松比调整效果。从图9中可以看出，最大应力的位置出现在纵向椭圆的长轴端点处。根据前期的测试，以20束/cm的复合膜为例，材料的经向拉伸强度约为254.52 Mpa。能满足绝大多数工程应用的强度要求。

3 结论

1)通过正交椭圆孔阵列设计的几何参数变化，分析了4种薄膜经纬双向等效泊松比的变化规律。4种薄膜胞元的经纬双向等效泊松比，在同一g值下随r值的变化均遵循①缓慢减小；②减小趋势加剧；③逐渐趋于稳定。在g值等于胞元边长的15%～20%时，3个过程均清晰可见。当g值偏小时，①过程不明显；当g值偏大时，③过程不明显。

2)对同一种薄膜而言，打孔后的泊松比主要由两个因素支配：孔间边界距离g，椭圆长半轴a与长短半轴长度之和(a+b)的比例r。

3)g值对薄膜胞元的泊松比的影响体现在两个方面：第一，g值决定了材料参数对打孔后的等效泊松比的影响程度；第二，胞元在旋转时，绕着孔间边界区域旋转，宽度越宽，相当于对胞元的约束程度越大，越不利于胞元的旋转；固定r，g值越大，等效泊松比也越大。

4)r值影响胞元旋转能力体现在当椭圆纵横比变大时，椭圆受拉后形状的变化程度上。当胞元受到一个方向的拉伸载荷时，胞元中心的椭圆孔趋向于变成一个圆形，即被“拉开”，当椭圆的纵横比较小时，椭圆很容易达到“拉开”的上限；而当椭圆的纵横比较大时，椭圆被“拉开”后的形状较之未“拉开”时变化较大，所以带来的胞元旋转能力也较大。固定g，r值越大，等效泊松比越小。