考虑粘弹性泊松比的固体推进剂蠕变型本构模型①
2019-09-13崔辉如申志彬李海阳
崔辉如,张 斌,申志彬,李海阳
(1.国防科技大学 空天科学学院,长沙 410073;2.中国航天科工集团有限公司第九总体设计部,武汉 430040)
0 引言
固体推进剂是典型的粘弹性材料,其泊松比在结构分析中扮演着重要的角色。试验结果表明[1],推进剂粘弹性泊松比是与时间、温度、纵向应变水平及预紧力相关的量。此外,推进剂泊松比在千分位上的变化都会对药柱结构完整性分析带来重要的影响。然而,在实际发动机结构完整性分析中,泊松比常被处理成常数。由以上分析可知,弹性泊松比的假设势必会带来不合理的分析结果。因此,利用粘弹性泊松比替代弹性泊松比进行结构完整性分析是非常有必要的。
一些专家学者对不同弹性泊松比下推进剂药柱结构时间-温度相关的力学响应进行了研究,结果表明,当泊松比从不可压情况下的泊松比ν=0.5变化到可压情况下ν≠0.5时,泊松比对药柱结构分析会有特别严重的影响[2-3]。尽管以上分析说明了泊松比对药柱结构分析的影响,但粘弹性泊松比对药柱结构的影响问题依旧没有解决。Deng等[4-5]基于Pan等[6]测得的粘弹性泊松比,研究了考虑时间相关泊松比的推进剂本构模型,并采用增量有限元方法对药柱结构进行了有限元分析,结果显示,弹性泊松比计算得出的应力应变结果比粘弹性泊松比计算得出的应力应变结果小得多。
本文从粘弹性泊松比的定义出发,通过拉普拉斯变换,建立了考虑粘弹性泊松比的推进剂蠕变型本构模型。针对星孔发动机的点火增压工况,对粘弹性泊松比的影响进行了研究分析。
1 粘弹性泊松比
在线性粘弹性的情况下,时间相关泊松比可以定义为松弛试验中,单轴拉伸状态下横向变形与初始纵向定应变的比值[7]:
(1)

固体推进剂是典型的热流变材料,粘弹性泊松比等材料参数符合时温等效原理,即时间和温度的不同组合可得到相同的泊松比。这个原理可以表示为
ν(lgt,T)=ν(lgζ,T0)
(2)
其中,缩减时间ζ表示为
ζ=t/αT
(3)
式中αT为时间平移因子。
另一方面,为了描述时间因子的温度相关性,可利用WLF方程,得到温度相关的平移因子[8]:
(4)
式中T为当前温度;Ts为参考温度;C1和C2为材料参数。
粘弹性泊松比的Prony级数表示为
(5)

当Prony级数项数为5时,函数相关参数见表1。WLF方程在20 ℃下的材料常数C1和C2见表2。

表 1 材料常数Prony级数中的参数

表 2 WLF方程参数
一个完整的本构模型必须有2个以上的独立材料参数。对于蠕变模型,蠕变模量和泊松比是必不可少的。蠕变模量用Prony级数表示为
(6)

当Prony级数的个数为3时,函数的系数列于表1中。此外,对蠕变模量WLF方程的材料常数列于表2。为了方便计算,定义:
(7)
2 蠕变型本构关系
对于均匀各向同性的粘弹性材料,考虑弹性泊松比,以蠕变模量和泊松比作为参考变量,剪切蠕变模量χ(t)和体积蠕变模量B(t)被定义为
χ(t)=2(1+ν)J(t)
(8)
B(t)=3(1-2ν)J(t)
(9)
但考虑到粘弹性泊松比的影响,式(8)在复域中形式为

(10)
利用逆拉普拉斯变换,式(10)可简化为
[1+ν(0)]J(t)*dSij+J*(t)*dSij=eij
(11)
其中
(12)
考虑到温度的影响,式(12)变为
(13)
其中,θ、θ′、ξ和ξ′为缩减时间。
同样地,对于复数域的蠕变模量:

(14)
粘弹性本构模型中的球形应变如下:
(15)
3 应用分析
为了验证新提出的蠕变型本构模型以及对粘弹性泊松比的影响特性进行分析,选择发动机点火增压工况作为主要研究内容。固体火箭发动机主要由壳体、绝热层和药柱等部件组成。为简化模型和计算方便,采用发动机的轴对称模型。采用六面体单元,对发动机几何模型进行网格划分,有限元模型如图1所示,该模型包含25 055个六面体单元和31 046节点。在模型的尾部施加轴向的位移约束,在对称剖面上施加环向位移约束。

图1 固体火箭发动机的有限元模型
表3列出了发动机中各材料的材料参数。两个弹性泊松比(粘弹性泊松比的初始值和平衡值)和粘弹性泊松比ν(t)将会被用来进行结构分析。

表3 固体火箭发动机的材料参数
发动机的建压曲线满足p(t)=p0(1-e-kt),其中p0=6 MPa,k=0.1 s-1。这里分析时间取t=300 s,主要是为了研究响应对时间的依赖性。
推进剂内表面的应变和应力分布是结构完整性的重要分析指标。应变或应力的急剧变化可能会导致非常危险的情况。因此,在发动机内表面选取特征线作为研究发动机内表面的应力应变变化的主要对象,如图2所示。

图2 固体火箭发动机内表面特征线示意图
ν=0.397 7和ν=0.486 4分别代表了粘弹性泊松比的初始值和平衡值。图3给出了第300 s时发动机内表面特征线上的Von Mises应力应变分布。由图3可发现,粘弹性泊松比引起的Von Mises应力应变响应介于两个弹性泊松比引起的Von Mises应力应变响应之间。而由粘弹性泊松比导致的Von Mises应力应变响应明显高于平衡泊松比引起的应力应变响应。初始泊松比引起的最大Von Mises应力应变分别为1.55 MPa和49.9%,这与粘弹性泊松比引起的最大Von Mises应力1.40 MPa,应变46.0%接近。另外,三种泊松比引起的最大Von Mises应力应变都发生在翼槽位置。从图3还可发现,由弹性泊松比和粘弹性泊松比导致的Von Mises应力应变在内表面特征线上的分布是一致的。也就是说,粘弹性泊松比并不会导致Von Mises应力应变的突变。此外,从图3中可明显看到松弛型(R)和蠕变型本构(C)的计算结果一致,这也说明了本文提出的蠕变型本构的准确性。
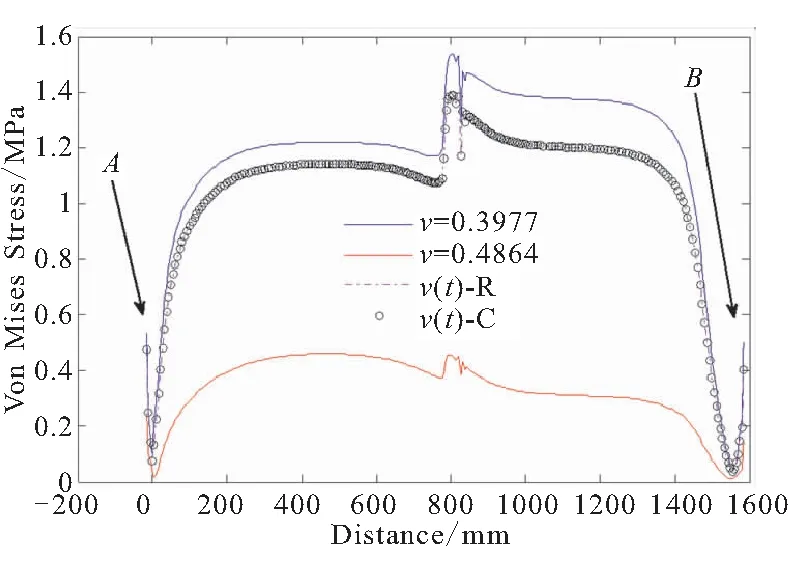
(a)Von Mises应力分布

(b)Von Mises应变分布
4 结论
本文从经典粘弹性本构模型出发,利用拉氏变换方法推导出了考虑粘弹性泊松比影响的固体推进剂蠕变型本构模型。该本构模型可考虑不同类型的泊松比(弹性泊松比和粘弹性泊松比)。基于MSC.Marc二次开发技术,将提出的本构模型应用到有限元分析中。针对星孔发动机点火增压工况,设计了三种泊松比(粘弹性泊松比及其对应的初始泊松比,平衡泊松),并对这些泊松比的影响进行了分析并得到以下结论:
(1)弹性泊松比与粘弹性泊松比引起的应力应变分布趋势一致。粘弹性泊松比在发动机结构完整性分析中并不会引起Von Mises应力应变在分布上的突变。
(2)粘弹性泊松比引起的Von Mises应力应变介于初始和平衡泊松比引起的Von Mises应力应变之间,并且与初始泊松比引起的Von Mises应力应变很接近。即对于极短时间内的点火增压工况,可以利用初始泊松比代替粘弹性泊松比进行结构完整性计算。
(3)仿真结果表明,本文提出的蠕变型本构模型可精确用于发动机结构完整性分析,为后续研究提供指导。
