封闭腔内声场的核心变量及其应用研究∗
2019-02-15高书娜
高书娜
(1.西南大学工程技术学院,重庆 400716; 2.汽车噪声振动和安全技术国家重点实验室,重庆 401122)
前言
锁定车身结构关键区域,进而快速提出改进措施以降低车内低频噪声,是当前车身低频声控制的一个研究热点[1-3]。前期研究提出一种基于声压幅度判定参数的车身低噪声设计方法[4-5],源于对封闭腔内声场计算公式的详细分析。
然而,并未见深入分析声场计算公式的变量及其与腔内声压响应的关系的文献[6-8],而这些则是进行腔内声压快速控制的重要前提。因此,本文中分析声场计算公式中的变量及其与公式中的4个参数和声压响应的关系,找出影响声压的核心变量;并通过物理样车的试验讨论核心变量的正确性;进而将研究结果应用到某型车的车内声压控制中,验证所找出的核心变量的合理性。
1 腔内声场计算公式的变量
极坐标下封闭腔内声场计算公式[5]为
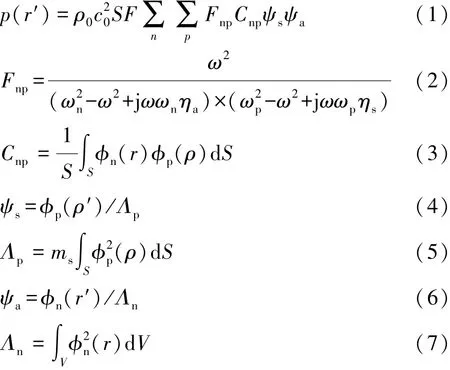
式中:ρ0为常温下空气密度;c0为常温下空气中的声速;S为结构声腔的接触面积;F为激励力;n为声腔的模态阶次;p为结构的模态阶次;Fnp为频率重叠系数;Cnp为振型耦合系数;ψs为结构振型在激励点处的分量;ψa为声腔振型在响应点处的分量;ω为激励力的圆频率;ωn为声腔固有频率;ωp为结构固有频率;ηa为声音传播介质的损失因子;ηs为结构损失因子;φn为声腔振型;φp为结构振型;ms为结构面密度;V为声腔体积。
观察式(1)~式(7),可以看出 ρ0,c0,S,F,ω,ωn,ωp,ηa,ηs,φn(r),φp(ρ),ms等 12 个量是主要输入量。 其中 ρ0,c0,ηa,ηs,ms等 5个量是空气、结构的材料密度、声学参数等,一般为常数;S是声场和结构的接触面积,通常是定值;因分析单位激励下1~500Hz范围内的腔内声压响应,所以激励力F和激励频率ω也是定值;余下的 ωn,ωp,φn(r),φp(ρ)等4个量是声场、结构的固有频率、振型,是进行腔内低噪声设计的主要调整量,所以是封闭腔内声场计算公式的变量。
式(1)的求和符号内有4个参数:频率重叠系数Fnp,振型耦合系数Cnp,结构振型在激励点处的分量ψs,声场振型在响应点处的分量ψa。其中,频率重叠系数是关于激励频率、声场固有频率、结构固有频率的参数;其余三者是关于声场振型、结构振型的参数。以下将逐一分析固有频率变量与频率重叠系数、腔内声压响应的关系,振型变量与其余3个参数、腔内声压响应的关系。
2 固有频率变量的分析
2.1 频率变量与频率重叠系数的关系
式(2)中,假设声场的固有频率为1~50rad/s,结构的固有频率为1~50rad/s,激励频率取值为25rad/s;根据常见空气和结构的阻尼特性,ηa取值为0.01,ηs取值为0.03。计算出频率重叠系数,绘制其幅值图(见图1),图中纵坐标是频率重叠系数的绝对值,无量纲,以下同。观察图中曲线可得如下结果。
(1)声场和结构的固有频率与激励频率越接近,频率重叠系数的幅值越大,反之越小。
(2)若保持声场的固有频率不变,而将结构的固有频率降低或升高3Hz后,频率重叠系数的幅值将由5.33降低为约0.66(图1(b)中用圆圈标识出),降低了约7倍;若保持结构的固有频率不变,而将声场的固有频率降低或升高3Hz后,频率重叠系数的幅值将由5.33降低为约0.22(图1(c)中用圆圈标识出),降低了约23倍。可见,对结构或声场的固有频率改变3Hz后,频率重叠系数的幅值明显得到降低。
上述讨论的是声场、结构的固有频率取既定值的规律,还需进一步讨论具体耦合系统的情况。采用含一个弹性面的矩形结构声场耦合系统(见图2)作为讨论对象。

图2 矩形耦合系统模型
图2 所示矩形耦合系统的物理参数如下:声腔的边长分别是 lax=1.0m,lay=0.6m,laz=0.5m;弹性钢板的边长分别是lsx=1.0m,lsy=0.6m,钢板厚度hs=1.2mm。激励力 Fs=10N;激励力作用点 xf=0.3m,yf=0.2m;声腔内响应点 xr=0.7m,yr=0.4m,zr=0.4m;计算频率 1~500Hz,频率分辨率 1Hz。
分别计算出矩形耦合系统的声场、结构的固有频率,将激励频率取值为200Hz,ηa取值为0.01,ηs取值为0.03,计算出频率重叠系数,其幅值图见图3,观察图中曲线可得如下结果。
(1)声场和结构的固有频率与激励频率越接近,频率重叠系数的幅值越大,反之越小。这与前文的规律一致。
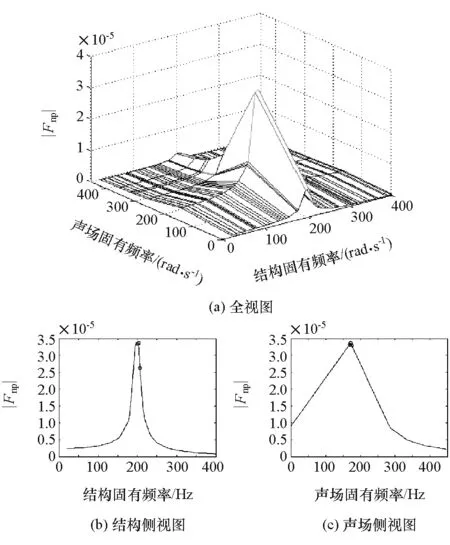
图3 矩形耦合系统的频率重叠系数
(2)结构固有频率分布较密,而声场固有频率分布稀疏(图3(a)中每一个交点即对应1阶频率)。这是常规物理耦合系统的特点。
(3)若保持声场的固有频率不变,而将结构的固有频率降低或升高3Hz,频率重叠系数的幅值改变量很小(图3(b)中用圆圈标识出)。同理,若保持结构的固有频率不变,而将声场的固有频率降低或升高3Hz,频率重叠系数的幅值几乎没有变化(图3(c)中用圆圈标识出)。可见,对于具体物理耦合系统而言,结构或声场的固有频率改变3Hz后,频率重叠系数的幅值几乎不受影响。
2.2 频率变量与腔内声压响应的关系
矩形耦合系统中,计算了结构第1阶固有频率、声场第1阶非零固有频率分别减少3和增加3Hz时腔内的声压响应,并与初始状态进行对比,结果见图4。

图4 固有频率调整前后的声压响应
观察图4中曲线可得如下结果。
(1)固有频率减小3Hz时,对应的峰值声压向低频移动3Hz,但声压大小几乎不变;反之,增加3Hz则峰值声压向高频移动3Hz,声压大小亦几乎不变。
(2)两种情况下,除了对应的峰值声压会移频外,曲线上其余的声压响应则几乎没有变化。
可见,调整固有频率,仅仅起到峰值声压移频的作用,而不能实现降低声压的目的。
2.3 小结
该部分基于公式以矩形耦合系统为对象,分析了固有频率变量与频率重叠系数、声压响应的关系,主要结论有:
(1)当声场和结构的固有频率与激励频率越接近时,频率重叠系数的幅值越大,反之越小;
(2)固有频率的改变,仅能使峰值声压移频,而难以降低腔内声压。
3 振型变量的分析
虽然振型涉及整个对象各处的相对变形量,但是研究发现振型的关键是节线的分布情况,所以将振型变量转化为对节线分布的讨论。节线是指在弹性体的各阶主振型中,除开被约束的位置,保持位置不变的点连成的线;节线分布是这些线的数量和位置。以四边简支钢板为例对节线及其分布进行详细说明。
(1)简支板的第1阶主振型如图5(a)所示。观察该阶振型,除开四周被约束的位置,在弹性板内部,没有保持位置不变的点(即变形量为0的点),所以它的节线数为零。
(2)简支板的第2阶主振型如图5(b)所示。观察该阶振型,除开四周被约束的位置,在弹性板的左右对称线上有保持位置不变的点,这些点可连成一条线,并正好与左右对称线重合,它是一条节线,且垂直于横轴。
(3)简支板的第4阶主振型如图5(c)所示。观察该阶振型,它有1条垂直于纵轴的节线。
(4)简支板的第5阶主振型如图5(d)所示。观察该阶振型,垂直于横轴、纵轴各有1条节线。
(5)简支板的其余各阶主振型的节线及分布可以此类推。

图5 简支板典型的主振型和节线分布
矩形耦合系统中的声场、简支板的振型均可用函数描述(见文献[8]),变量是各边上的节线数,该耦合系统的振型变量可进一步细化成节线数。以下将以矩形耦合系统为对象,讨论节线数的改变(即节线分布改变)对各参数、声压响应的影响规律。此外,因声场中难以实现低频零值声压的物理约束,所以不讨论声场振型的节线分布改变的情况。
计算了简支板的两条边各增加1条振型节线(相当于添加了“+”形加强筋)前后,矩形耦合系统的振型耦合系数、激励点处振型分量、声压响应,结果见图6。

图6 增加节线后的计算结果
观察图6中曲线,发现增加节线数后:
(1)振型耦合系数整体明显降低,是声场计算公式的关键参数;
(2)激励点处振型分量有的增加、有的减小;
(3)200Hz以内的低频声压响应明显降低。
可见,增加节线数,对封闭腔内的声压影响明显,可显著降低低频声压。因此,节线数或节线分布是封闭腔内声场的核心变量,是进行腔内低频噪声控制时的重点研究对象。
4 试验验证
为验证增加节线数可降低低频声压,制作一简化车身的试验样车,如图7(a)所示。该样车的底面为弹性钢板,其余为刚度较大的有机玻璃。其中,车身骨架采用角钢;封闭声腔的各个面,除底面外,均采用板厚10mm的有机玻璃;底面可拆卸更换,制作了板厚2mm的平面底板、装有“+”加强筋的底板各1张。
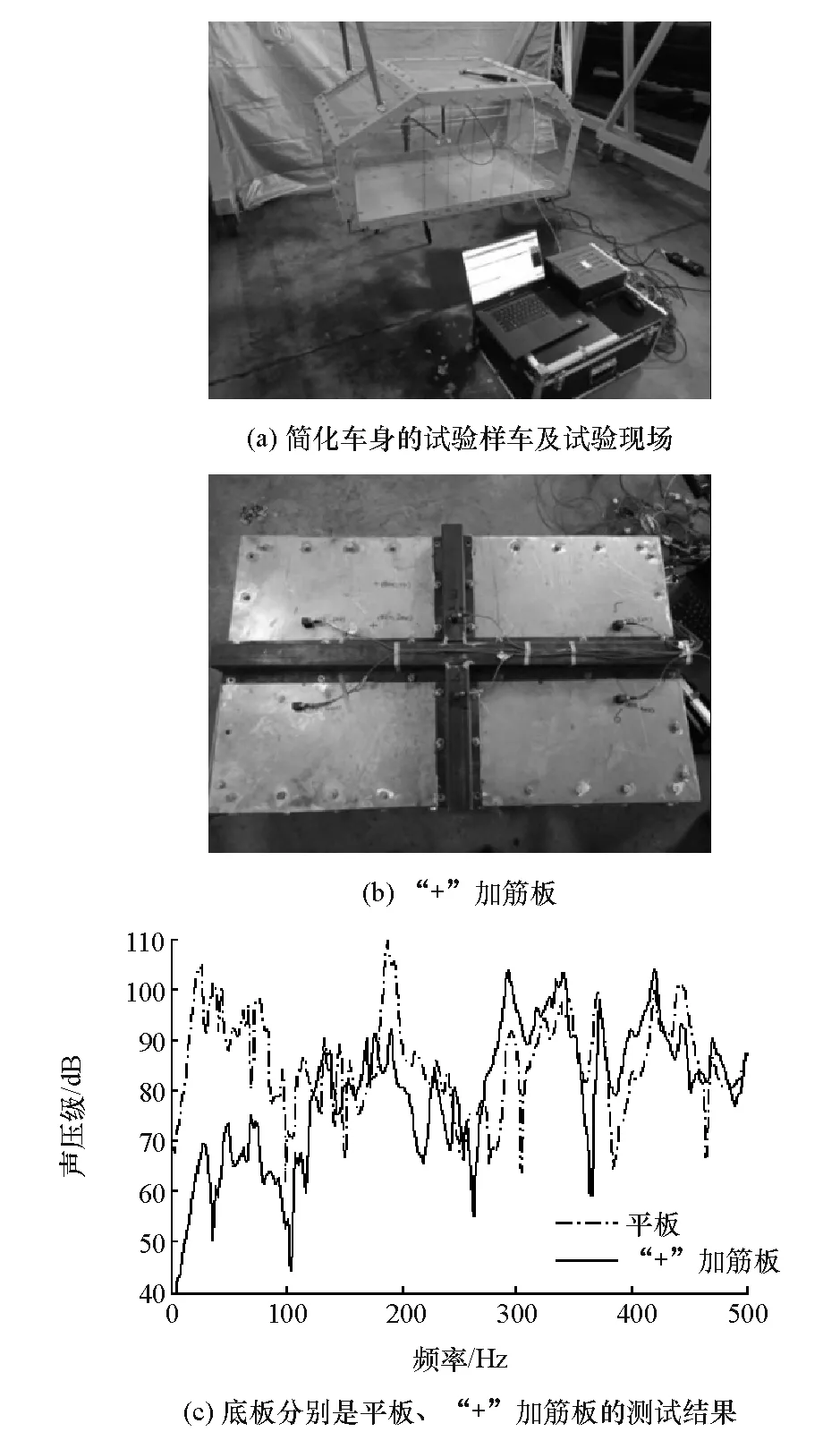
图7 试验样车、试验现场及测试结果
利用LMS的振动噪声测试设备,测试了样车的底板分别是平板、“+”加筋板两种状态下,以力锤作为输入激励,同一测点的声压传递函数,试验现场如图7(a)所示。试验过程中,样车采用弹性绳柔性悬吊。
试验结果见图7(c)。可见,在弹性平板添加“+”加强筋后,200Hz以内的低频声压有明显降低,这与图6(c)的计算结果一致,从而验证了增加节线数可降低腔内声压。
5 在车内低频噪声控制中的应用
建立的某两厢车的车身结构有限元模型、声场有限元模型见图8(a)和图8(b)(文献[9]中对该车身的有限元模型进行了试验验证),该两厢车在单位激励下典型测点的声压响应曲线见图8(c)。
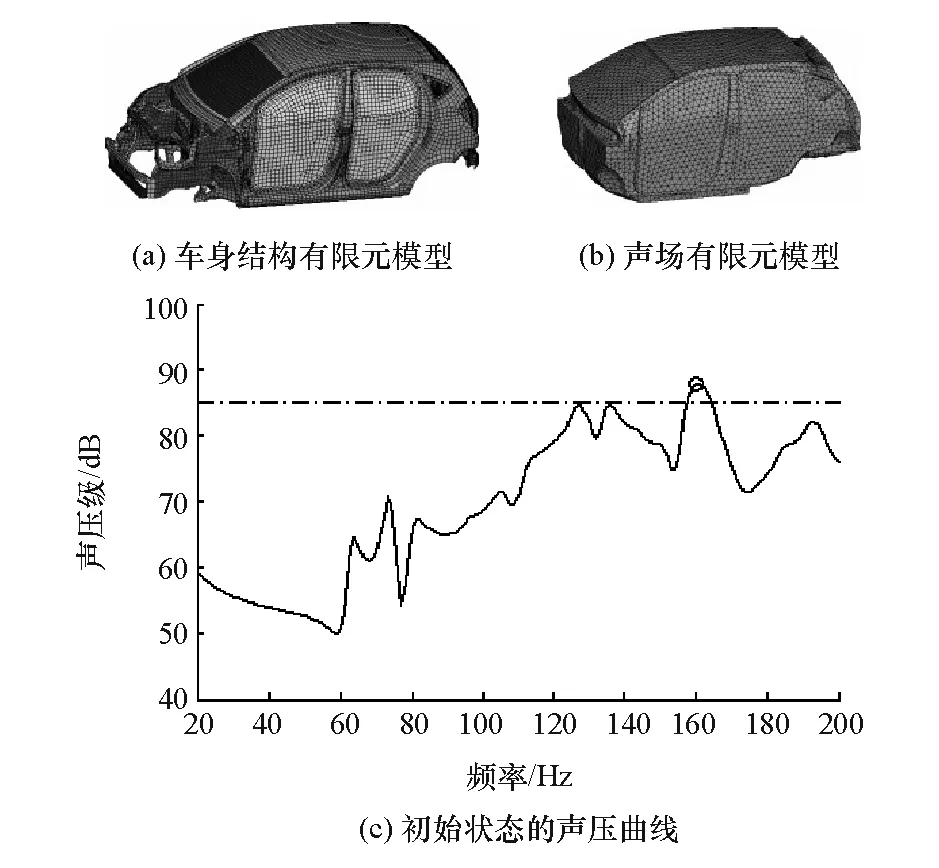
图8 某两厢车有限元模型及车内声压
不妨假设此工况下其声压目标是在0~200Hz范围内,响应点的声压不超过85dB。此时,初始结构在160Hz上出现了超出目标曲线的峰值声压。根据前文讨论结果,想要降低峰值声压应从增加节线数的角度提出结构改进措施。
经过分析发现第8阶、第9阶和第14阶结构模态是关键模态,它们在耦合面上的振型分量见图9,可见这几阶模态的振型腹部分布在B柱、底板区域。在这些区域增加节线数,具体改进措施即为添加加强筋,加强筋位置示意图见图10(a)和图10(b),改进后典型测点的声压响应曲线见图10(c)。可见,在振型腹部添加加强筋后,声压响应降低到目标范围内,验证了增加节线数可降低腔内声压这一重要结论;并且,结构改进措施的提出快速准确。
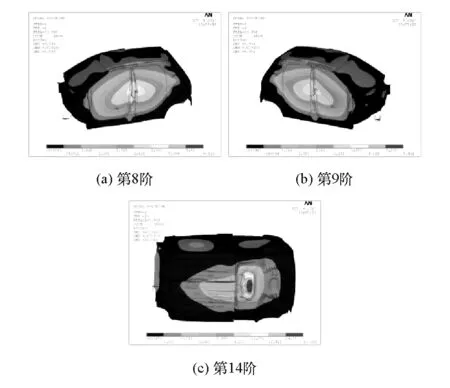
图9 某两厢车关键结构模态在耦合面上的振型分量

图10 某两厢车的结构改进和改进后的车内声压
6 结论
基于声场计算公式,讨论公式中的变量与各参数、声压响应的关系,找出了声压的核心变量,并将研究结果应用到某型车的车内声压控制中,主要结论如下:
(1)固有频率变量对声压响应的影响较弱,仅能起到峰值声压移频作用,而难以降低腔内声压;
(2)振型变量的关键是节线分布,增加节线数通常可明显降低腔内声压响应,节线分布是封闭腔内声场的核心变量;
(3)简化车身的物理样车试验,验证了增加节线数可降低腔内低频声压;
(4)利用上述结论指导某型车的车内声压控制,在关键结构模态的振型腹部添加加强筋后,声压响应降低到目标范围内,进一步验证了封闭腔内声场的核心变量是节线分布这一结论。
