深海直达声区中大深度声场水平纵向相关特性

王梦圆，李整林，秦继兴，吴双林，王光旭

(1.中国科学院 声学研究所 声场声信息国家重点实验室，北京 100190；2.中国科学院大学，北京 100049)

0 引言

声场水平相关特性描述了水平方向上具有一定间距两个接收点处接收信号的相似程度。在实际海洋环境中，海水介质的随机不均匀性和多途干涉效应会使声场的水平相关性降低，进而影响阵列信号处理增益和对水下目标的探测性能。因此，声场水平相关特性一直是国内外海洋声学工作者的重要研究内容。

Wille等[1]研究了浅海水平横向相关长度与声信号频率的关系，结果表明浅海水平横向相关长度随信号频率的增大而减小。Carey[2]对深海声场和浅海声场的水平横向相关半径进行了对比分析，发现当深海传播距离是浅海的10倍时，深海横向相干半径至少是浅海横向相干半径的3倍。Gorodetskaya等[3]通过数值仿真研究了深海远距离声场水平相关性对水平阵处理增益的影响，研究发现粗糙海面散射效应对声场相关性影响较大。Colosi等[4]仿真分析了菲律宾海深海环境下声场相干性问题，研究发现声场的水平纵向相干半径与频率的负1次幂和距离的负1/2次幂呈正比。尚尔昌[5]分析了随机浅海信道中声场横向相干理论，推导了环境变化对声信号水平横向相关性影响的解析表达式。Wang等[6]研究了多途干涉和声散射对浅海声场水平相关性和垂直相关性的影响，结果表明在浅海中长距离处水平纵向相关半径大于垂直相关半径。Zhu等[7]利用简正波和射线理论分析了浅海声场的水平横向相关特性。李秀林等[8-9]利用光纤阵列接收到的气枪信号分析了浅海声场水平相关性，并利用声场的水平相关性反演海底参数。苏晓星等[10]和Zhang等[11]研究了浅海声场的水平纵向相关性频移补偿方法。

近年来水声工作者开展了较多的深海声学实验，对深海声场水平相关性的研究也逐渐加强。Li等[12-13]使用一次南海深海声传播实验数据，分析了180 km范围内1 800 m以浅深度的声场水平相关性，结果表明深海声场空间相关系数的分布与传播损失空间分布基本一致。王域等[14]研究了深海声场水平相关半径对被动合成孔径性能的影响，结果发现在深海会聚区内声场水平相关半径较大，被动合成孔径的探测性能相对常规物理孔径基阵有明显改善。另外，Hu等[15]研究了南海深海复杂地形环境下的声场水平纵向相关特性，Yang等[16]研究了西太平洋深海环境中的声场水平纵向相关性。

通常声场水平相关性是水平横向相关和水平纵向相关的叠加，但水平阵的性能主要受限于声场的水平纵向相关性。

本文主要研究声场的水平纵向相关性。利用2016年冬季南海一次深海不完全声道实验的数据，通过实验数据和数值仿真分析深海大深度声场的水平纵向相关特性，并根据射线理论对深海直达声区声场水平纵向相关系数进行理论推导，研究结果对深海海底水平阵设计和深海水声目标探测具有重要意义。

1 实验概况

2016年11月，某实验室在中国南海深海进行了一次深海声传播实验，实验采用单船(“实验1号”)结合潜标的方式，实验设备布放示意图如图1所示，实验过程中船速约为4 kn.实验采用18元的潜标垂直阵，非等间隔地布放在99～4 152 m深度范围内，接收水听器的采样率为16 kHz，其中布放在4 152 m深度处水听器的灵敏度为-180 dB，其他深度处为-170 dB.图1中，XCTD为抛弃式温盐深仪。声源为拖曳换能器发射的双曲调频信号，声源级为193 dB，中心频率为300 Hz，带宽为100 Hz.

图1 实验设备布放示意图

发射信号的时间序列如图2所示，单个信号时长20 s，相邻两个信号间隔20 s，每4个信号为一组，间隔50 s发射下一组信号。实验过程中拖曳声源的平均深度约为120 m，最远发射距离为182 km.“实验1号”由远及近驶向垂直接收阵，实验过程中海深变化如图3所示，可见在30 km距离内海底较为平坦，平均海深约为4 312 m.实验中用XCTD在站点处测量的声速剖面如图4所示，可以看出声道轴大约位于1 151 m深度处，声道轴处声速为1 484 m/s，海面处声速为1 540 m/s，海底处声速为1 533 m/s，小于海面处声速，为典型的深海不完全声道。

图2 发射双曲调频信号的时间序列

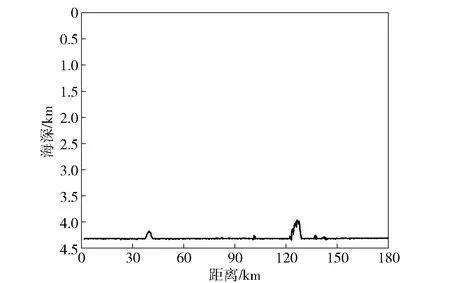
图3 声传播方向上的海深

图4 实验期间用XCTD测量的海水声速剖面

2 实验数据处理

假设声源发射的双曲调频信号为s(t)，则接收水听器接收到的信号sr(t)可表示为

(1)

式中：S(ω)为s(t)的频谱，ω为角频率，t为时间；P(r,z;ω)为声源到接收器的水声信道的传输函数，r为水平距离，z为深度。数据处理先对接收信号进行脉冲压缩提高信噪比，得到脉冲压缩后的信号为

(2)

然后对sc(t)作傅里叶变换，得到频谱Xi，将Xi在发射信号带宽(100 Hz)内取平均值，得到接收信号经脉冲压缩后的平均能量为

(3)

式中：f0为发射信号的中心频率；Fs为采样率；fu和fd分别为发射信号频率的上、下限；nfu和nfd为频点数。则接收声信号的传播损失为

TL(f0|(r,z))=SL(f0)-(10lg[E(f0)]-Mv-Ec)，

(4)

式中：SL(f0)为发射换能器声源级；Mv为接收水听器的灵敏度；Ec为脉冲压缩的时间带宽增益。

根据上述实验数据处理流程对接收到的实验信号进行处理，得到接收深度为4 152 m时的声传播损失，如图5中红色点线所示。使用抛物线方程近似声场模型(RAM-PE)[17]，根据互易原理计算声传播损失，仿真时声源深度为4 152 m，接收深度为120 m，频带范围与实验中的发射信号一致，为250～350 Hz，选取21个频点。仿真时采用的声速剖面如图4所示，海底参数选取如下：声速1 565 m/s，密度1.6 g/cm3，吸收系数0.3 dB/λ[18].图5给出了接收深度为4 152 m时声传播损失仿真与实验对比，可以看出传播损失实验值与仿真值符合较好。图6给出了RAM-PE计算的二维声传播损失图，可以看出随着接收深度变大，直达声区的水平宽度变宽，当接收深度为4 152 m时，直达声区的水平宽度可达到30 km，而且在30 km内的声传播损失皆小于83 dB，有利于水下目标探测。但为了提高对水下弱目标的探测能力，往往需要设计水平阵列获取较高的增益，而声场水平纵向相关性是设计水平阵的重要参数，因此第3节将重点研究深海直达声区大深度声场的水平纵向相关特性。

图5 接收深度为4 152 m时传播损失仿真与实验对比

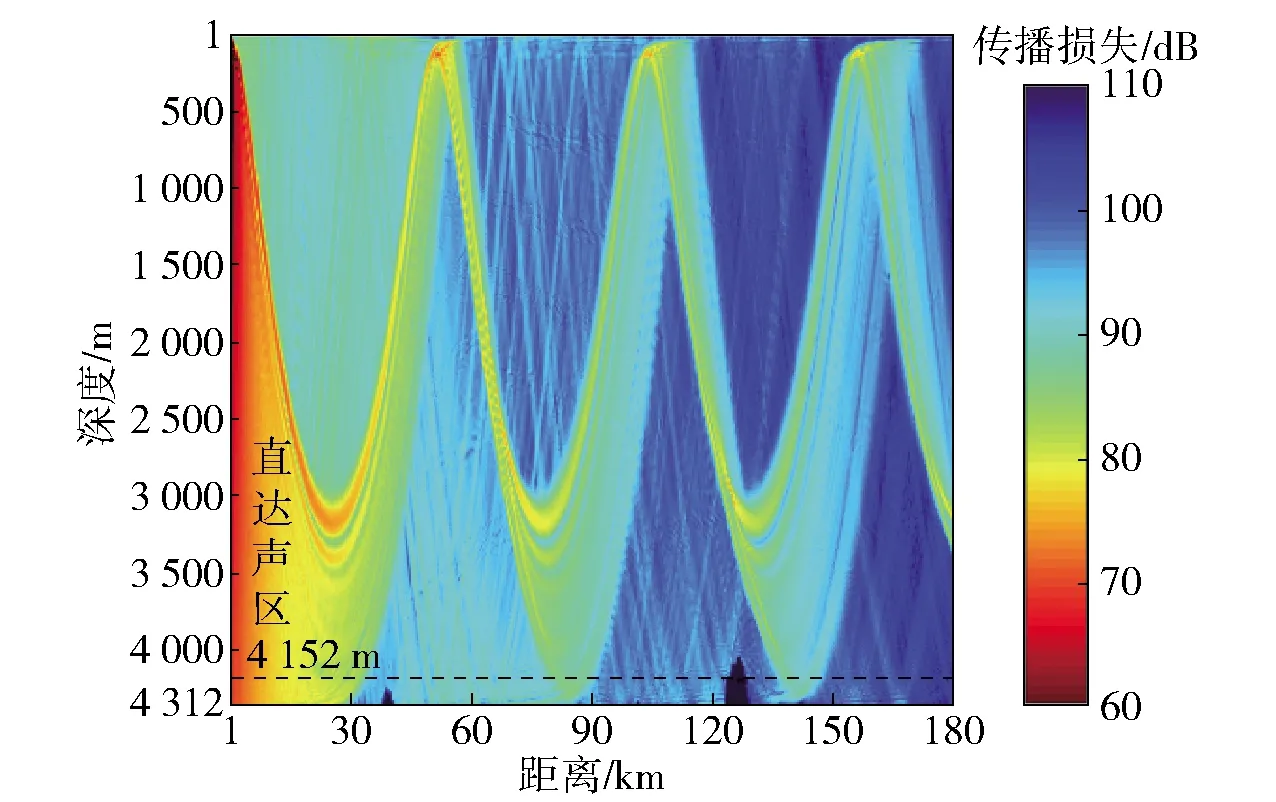
图6 RAM-PE仿真的二维传播损失

3 大深度声场水平纵向相关系数

3.1 声场水平纵向相关系数定义

声场水平纵向相关系数是指在同一接收深度处，沿声传播方向上不同水平距离r处接收信号之间的归一化互相关系数，可表示为

(5)

式中：pr(t)和pr+Δr(t+τ)表示不同水平距离处接收信号的时域声压值，Δr为水平纵向间隔，τ为时延。经过傅里叶变换后，得到水平相关系数的频域表达式为

ρ(Δr)=

(6)

3.2 仿真分析和实验验证

利用抛物方程模型RAM-PE对直达声区30 km内接收深度为4 152 m时的声信号进行仿真，声源深度120 m.仿真时用的声速剖面和海底参数与图6的数值计算一致，频带范围仍为250～350 Hz，选取501个频点，频点间隔为0.2 Hz，仿真信号时长5 s.根据(6)式计算的声场水平纵向相关系数二维图如图7所示，水平参考距离从1 km变化到100 km，覆盖大深度声场的直达声区、影区和会聚区，水平纵向间隔步长为10 m，最大水平纵向间隔为1 000 m.对比图7和图6可以看出，大深度声场的水平纵向相关系数与声能量不呈正相关的关系，换言之，并不是声能量大的区域相关系数就高。另外由图7可以看出，大深度直达声区声场水平纵向相关系数随纵向间隔的增加存在明显的振荡结构。图8给出了参考水平距离为10 km和29 km时水平纵向相关系数仿真与实验对比。由图8可以看出：仿真结果与实验结果较为符合；在直达声区，远距离29 km处的声场水平纵向相关半径明显大于近距离10 km处的声场水平纵向相关半径。图9给出了直达声区大深度声场频率距离二维分布图，声场的大小用传播损失表征(dB)。由图9可以看出：直达声区大深度声场存在明显的干涉结构，因此导致声场水平纵向相关系数存在周期性的振荡结构；当两个距离处的声场存在相同的干涉特性时，声场的相关系数达到最大，反之声场相关系数降到最小。

图7 水平纵向相关系数随水平参考距离和纵向间隔变化的二维图

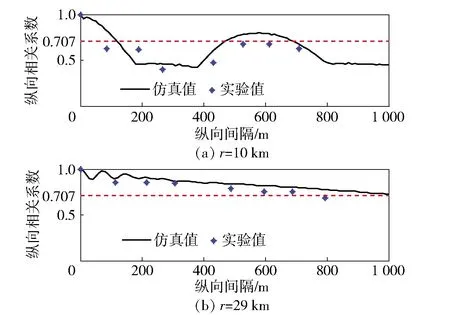
图8 不同水平距离下水平纵向相关系数仿真与实验对比

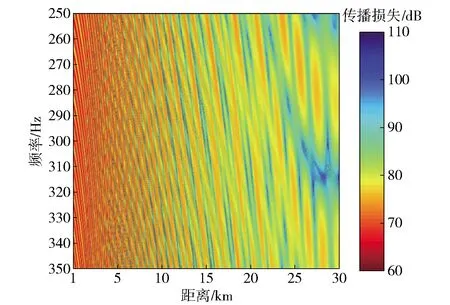
图9 直达声区大深度声场频率-距离二维图

4 直达声区水平纵向相关特性分析

为了进一步分析深海直达声区大深度声场水平纵向相关特性，通过理论推导和数值仿真研究不同声源频率、不同声源深度和不同接收深度下直达声区大深度声场水平纵向相关特性。

4.1 理论分析

深海直达声区声场主要由直达波和海面反射波组成，假设直达波与海面反射波幅值近似相等，则距离为r、接收深度为z处的声强[16]可表示为

|p(r,z,ω)|2=2A2[1-cos(ωΔtr)]，

(7)

式中：A为直达波和海面反射波的幅度；Δtr为距离r处直达波与海面反射波的到达时间差。若不考虑直达波和海面反射波的幅值随频率的变化，则水平纵向相关系数[16]可以表示为

(8)

式中：ω0为发射信号中心角频率，ω0=2πf0；Δtr+Δr为距离r+Δr处直达波与海面反射波的到达时间差。

为了简化推导，假设声线直线传播，声源和接收器的相对位置如图10所示。图10中，s是声源，s′是虚源。则Δtr可表示为

图10 声源与接收器相对位置示意图

(9)

式中：zs表示声源深度；zr表示接收深度；c0表示声源到海面间的平均声速。

(9)式求导，可得到Δtr-Δtr+Δr的表达式为

(10)

(10)式代入(8)式，可得

ρ(r,r+Δr,ω)=

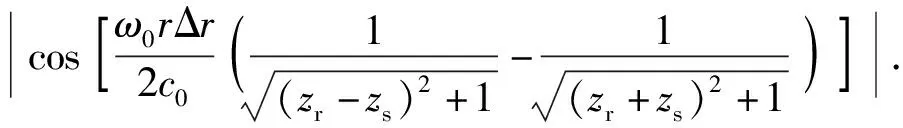
(11)

由(11)式可以得出结论：深海直达声区水平纵向相关系数存在周期性的振荡结构，振荡周期随发射信号中心频率f0的增大而减小。

4.2 仿真分析

4.2.1 声源频率变化对深海直达声区大深度声场水平纵向相关性的影响

仿真时声源深度为120 m，接收深度为4 152 m，声源中心频率分别取50 Hz、100 Hz和300 Hz，带宽取1/3倍频程，最大水平纵向间隔为2 km，得到的声场水平纵向相关系数二维图如图11所示。由图11可以看出，声场水平纵向相关系数存在振荡结构，而且当声源深度和接收深度不变时，声源频率增大导致声场水平纵向相关系数的振荡周期减小，与4.1节中的理论分析结果一致。由于第1个振荡周期的大小决定了不同参考距离处声场水平纵向相关半径的大小，可以看出当声源深度和接收深度不变时，声源中心频率越大，声场的水平纵向相关半径越小。

图11 不同中心频率下声场水平纵向相关系数二维图

为了进一步分析声场水平纵向相关半径随声源频率变化的原因，图12给出了RAM-PE仿真的声源深度为120 m以及声源中心频率分别取50 Hz、100 Hz和300 Hz时声场的传播损失二维图，仿真时声速剖面和海底底质参数的选取与图6相同，图中黑色虚线为接收深度为4 152 m处，可以看出直达声区声场存在干涉结构。对比图12(a)、图12(b)和图12(c)可以看出，随着声源频率增大，直达声区声场干涉条纹个数增多，条纹宽度变窄。对比图12和图11可以看出，声场干涉条纹个数越多，水平纵向相关系数的振荡周期越多。图13给出了图12(a)、图12(b)和图12(c)中黑色虚线处的声传播损失对比图。由图13可以看出，同一参考距离处，声源频率越高，声场传播损失的振荡周期越小，对应图10中的声场水平纵向相关半径越小，表明直达声区声场相关半径的大小与声场传播损失的振荡周期大小一致，传播损失振荡周期越大，声场水平纵向相关半径越大。

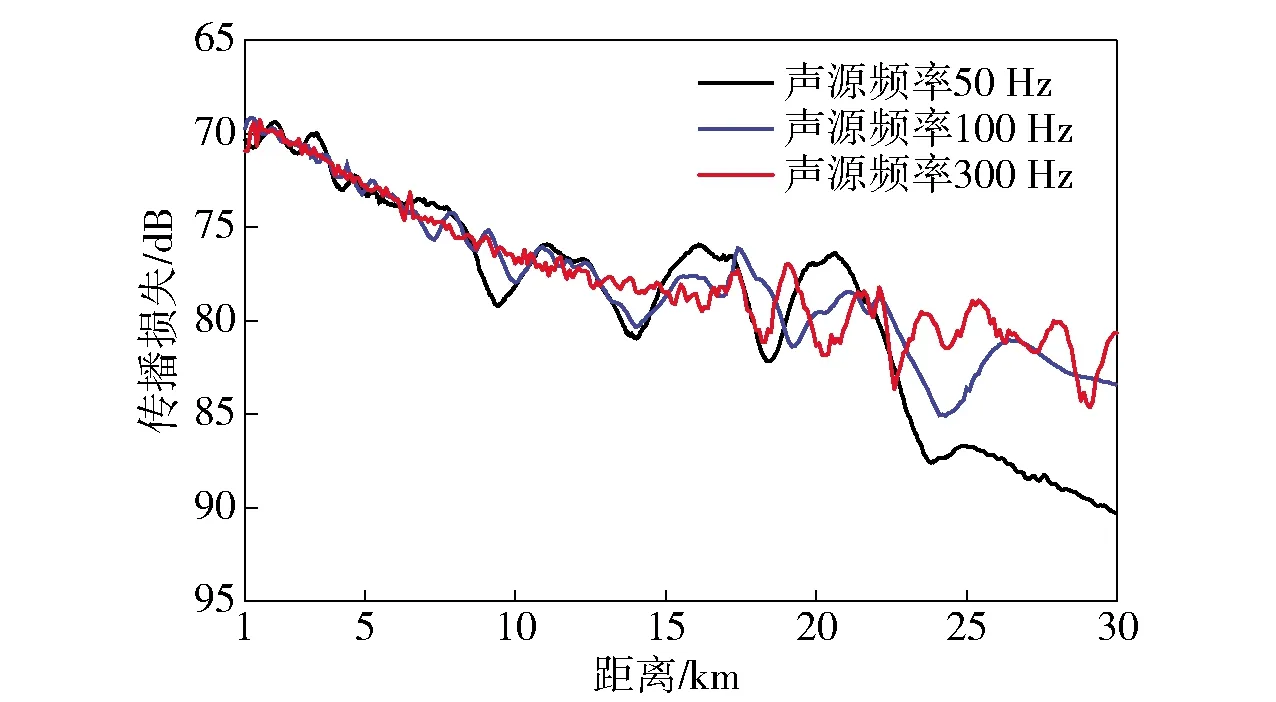
图13 不同中心频率下声场传播损失对比

4.2.2 声源中心频率和接收深度一定时不同声源深度下声场水平纵向相关系数

仿真时声源频率为100 Hz，接收深度为4 152 m，最大水平纵向间隔为2 km，声源深度分别取7 m、200 m和300 m，得到的声场水平纵向相关系数二维图分别如图14(a)、图14(b)和图14(c)所示。对比图14(a)、图14(b)、图14(c)可知，当声源频率和接收深度一定时，声场在近距离15 km内的水平纵向相关半径随声源深度变大而减小。

图14 不同声源深度条件下声场水平纵向相关系数二维图

为了进一步分析声场水平纵向相关半径随声源深度变化的原因，图15给出了RAM-PE仿真的声源频率为100 Hz时，声源深度分别取7 m、200 m和300 m时声场的传播损失二维图，仿真时声速剖面和海底底质参数的选取与图6相同，图中黑色虚线为接收深度为4 152 m处。由图15(a)可以看出，当声源深度为7 m、接收深度为4 152 m时，直达声区的水平宽度约为15 km，在15 km以内声场的干涉结构不明显，对应图14(a)中声场的水平相关半径较大；而在15 km后为非直达声区，接收器接收到较多经海底海面反射的能量，声场存在明显的干涉结构，导致图14(a)中声场的水平纵向相关系数存在干涉结构。对比图15(a)、图15(b)和图15(c)可以看出，随着声源深度的增大，直达声区声场干涉条纹的个数增多，条纹宽度变窄。对比图15和图14可以看出，声场干涉条纹个数越多，水平纵向相关系数的振荡周期越多。图16给出了图15(a)、图15(b)和图15(c)中黑色虚线处的声传播损失对比图，由图16可以看出，在深海直达声区范围内，对于同一参考距离，声源深度越大，声场传播损失的振荡周期越小，对应图14中的声场水平纵向相关半径越小，说明直达声区声场相关半径的大小与声场传播损失的振荡周期大小一致，与前面的也分析一致。

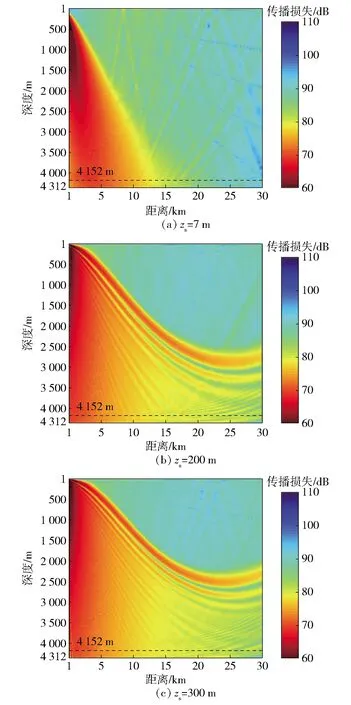
图15 不同声源深度条件下声场传播损失二维图

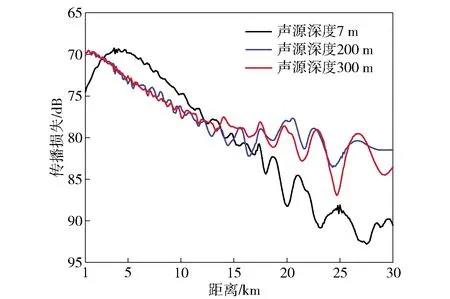
图16 不同声源深度条件下声场传播损失对比

4.2.3 接收深度变化对深海直达声区大深度声场水平纵向相关性的影响

仿真时声源中心频率为50 Hz，声源深度为300 m，接收深度分别为4 000 m、4 100 m、和4 250 m，得到水平纵向相关系数二维图如图17所示。对比图17(a)、图17(b)和图17(c)可以看出：接收深度的增大对直达声区近距离处声场水平纵向相关系数的振荡结构影响不大；随着接收深度变深，直达声区远距离处声场的水平纵向相关半径变大。

为了进一步分析声场水平纵向相关半径随声源深度变化的原因，图18给出了RAM-PE仿真的声源频率为50 Hz、声源深度为120 m时声场的传播损失二维图，仿真时声速剖面和海底底质参数的选取与图6相同。图19给出了图18中接收深度为4 000 m、4 100 m和4 250 m处的声传播损失对比。由图19可以看出：在直达声区近距离处，对于同一参考距离，接收深度变大，声场传播损失的振荡周期并未发生明显变化；在直达声区远距离处，接收深度变深，声场传播损失的振荡周期变大，对应图17中声场的水平纵向相关半径变大，同理也表明直达声区声场相关半径的大小与声场传播损失的振荡周期大小一致，与前面的分析一致。

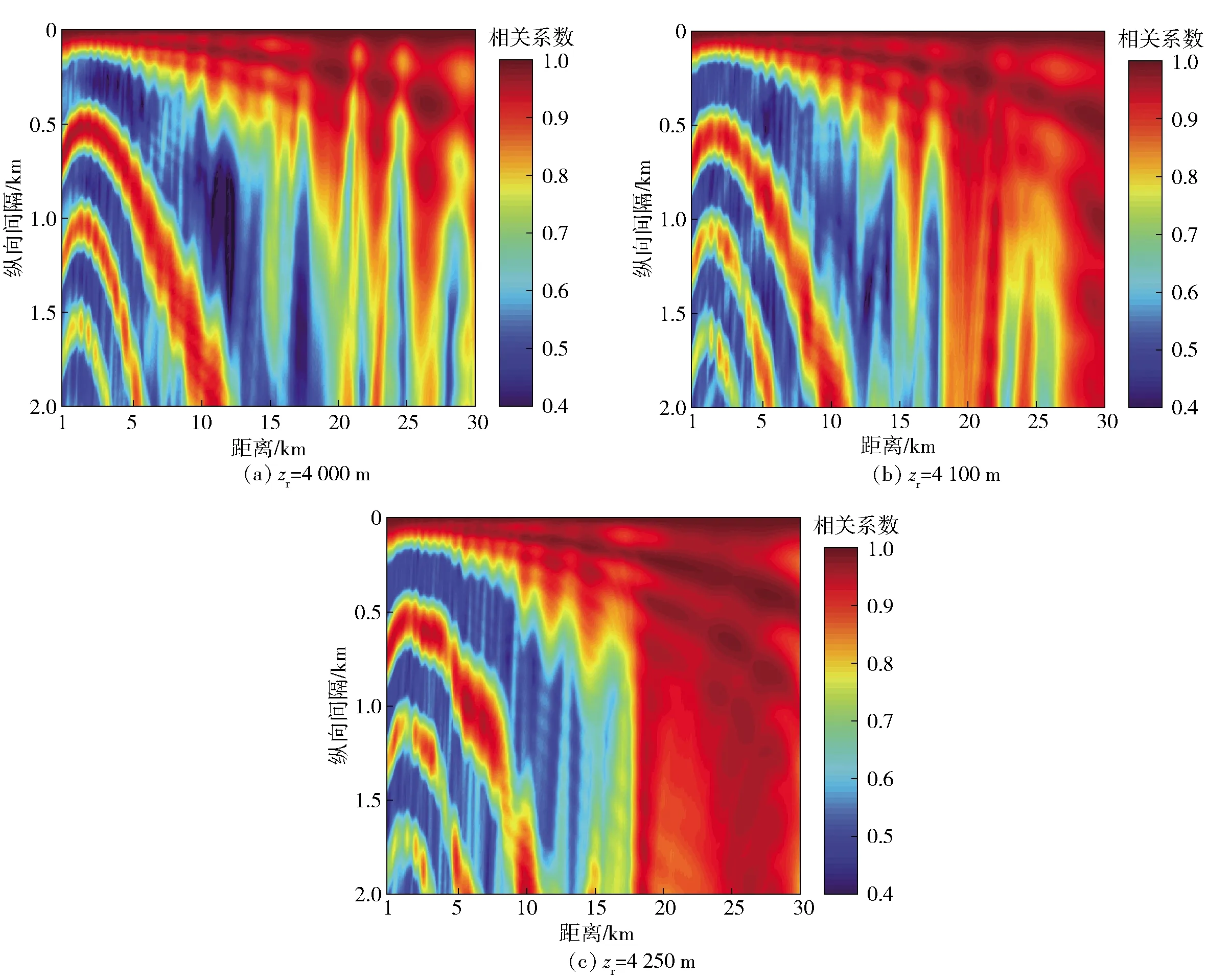
图17 不同接收深度时声场水平相关系数二维图

图18 声场传播损失二维图

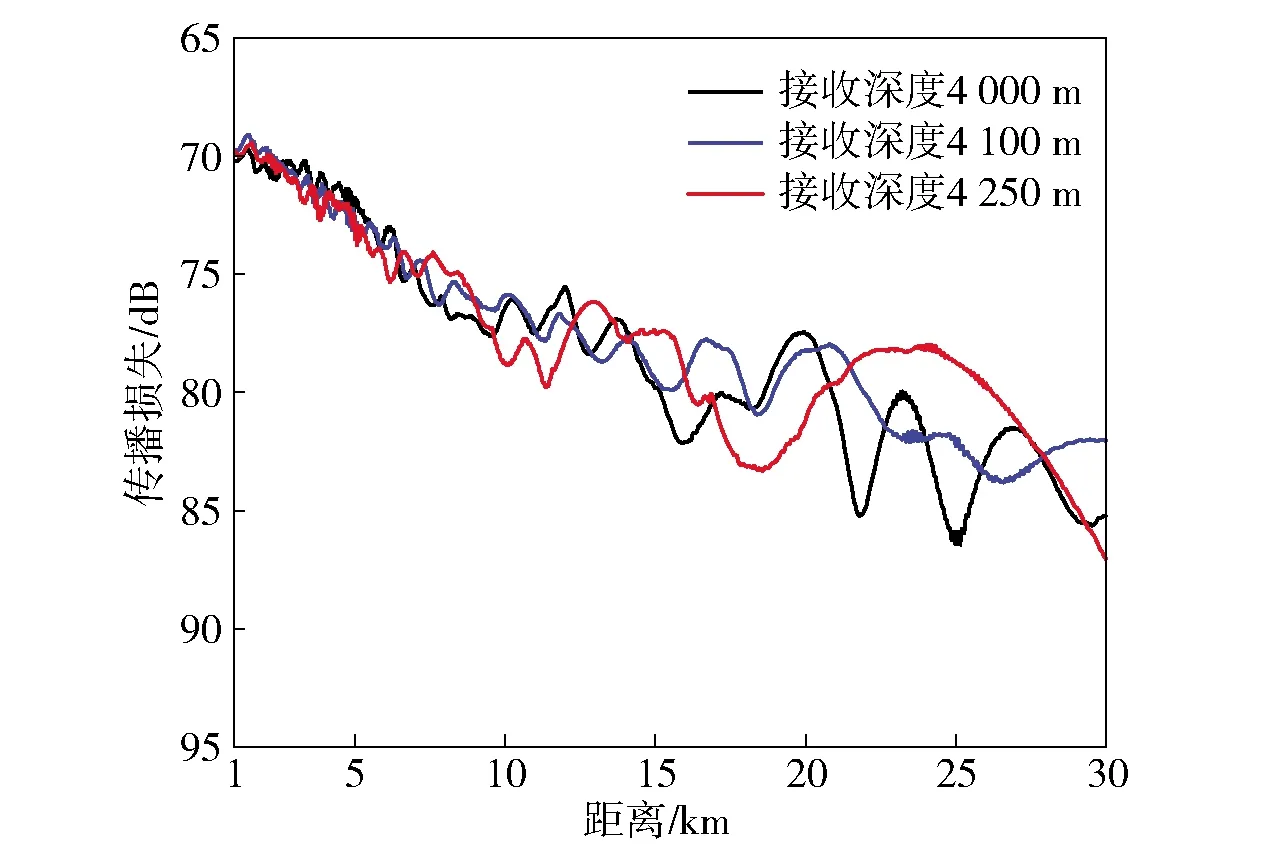
图19 不同接收深度时声场传播损失对比

5 结论

本文利用2016年冬季南海一次深海不完全声道声传播实验数据，结合理论推导和数值模拟分析了深海直达声区中大深度声场水平纵向相关特性。所得主要结论如下：

1)直达声区中大深度声场存在干涉结构，导致声场水平纵向相关系数存在振荡结构，且不同参考距离处水平纵向相关半径的大小与声场传播损失的振荡周期一致，传播损失振荡周期越小，声场的水平纵向相关半径越小，反之越大。

2)直达声区中大深度声场的水平相关半径大小受声源频率、声源深度和接收深度变化影响，当声源频率增大其他条件不变时，直达声区中大深度声场的水平纵向相关半径变小，当声源深度增大、其他条件不变时，直达声区中大深度声场水平纵向相关半径也变小，而当接收深度变大、其他条件不变时，直达声区近距离处的水平纵向相关半径不变，远距离处声场的水平纵向相关半径变大。