基于多传感器信息融合的汽车行驶状态估计∗
2019-02-15周卫琪
周卫琪,齐 翔
(1.江苏大学汽车工程研究院,镇江 212013; 2.江苏大学汽车与交通工程学院,镇江 212013)
前言
在当今我国的许多大城市,汽车的普及率达到了较高的水平,人们的日常生活已经离不开汽车。其中交通事故的发生问题较为突出。汽车主动安全服务与控制的出现为解决交通事故的发生提供了一种新的解决办法,而准确估计出车辆的行驶状态信息,可以保证汽车主动安全控制[1]。其中一些重要的车辆状态信息如质心侧偏角、横摆角速度、纵向车速及侧向车速等难以直接测量或者测量成本过高,为此利用一些低成本传感器结合融合估计算法对汽车行驶状态估计成为了汽车工程领域的研究热点[2]。
国内外学者已经对车辆状态信息的准确获取进行了大量的研究。运用新式车载传感器GPS/INS组合导航系统[3],这种方式在一定程度上提高了估计结果的精确性,但是成本较高不易普及。利用一些估计算法代替部分硬件测量,常见估计算法如卡尔曼滤波(KF)[4]、扩展卡尔曼滤波(EKF)[5-6]、无迹卡尔曼滤波(UKF)[7-8]、状态观测器[9],还包括智能算法如神经网络[10]、模糊逻辑[11]等。这些算法基于车辆模型对汽车的关键状态信息进行估计。由于车辆系统是一个强非线性系统,经典卡尔曼滤波仅能处理线性系统[12],EKF与UKF具有计算量大和受外部环境影响较大的问题,因此本文中采用了能够降低噪声影响的自适应无迹卡尔曼滤波(AUKF)算法。综上所述,在对车辆行驶中难测或测量成本较高的状态变量进行测量时,由于车载传感器成本或者精度的限制,同时受算法复杂程度在实际应用中的制约,车辆行驶状态信息具有一定的不完全性和不精确性。
因此,如何利用低成本车载传感器,通过必要的信息融合技术从不完全、不精确的观测信息中经济地提取出全面的、精确的车辆状态信息成为了目前意义重大的研究方向。信息融合也成为了一门迅速发展的学科,国内外学者提出了以其它理论为基础的信息融合算法,如Bayes估计、粒子滤波等[13-14]。考虑到观测信息及融合目标,本文中在3自由度车辆模型的基础上,利用AUKF理论建立了一种用于汽车行驶状态估计的信息融合算法。通过多传感器的信息融合,实现了质心侧偏角、横摆角速度和纵向车速的准确估计。经过仿真及实车验证了该算法的有效性,并且比EKF和UKF具有更好的精度和实时性。
1 AUKF算法与信息融合理论
1.1 信息融合技术
信息融合指的是利用计算机技术对按时序获得的若干传感器的观测信息在一定准则下加以自动分析、综合处理,以完成所需的决策和估计任务而进行的信息处理过程。其目标是基于各传感器检测信息分解人工观测信息,通过对信息的优化组合来导出更多的有效信息[15]。为了节约成本,将多个低成本传感器采集到的信息进行融合,得到需要的信息。在本文中,需要融合的信息通过车载传感器获得,即测量信息(转向盘转角、纵向加速度、侧向加速度)。将测量信息经过预处理后由基于AUKF的融合中心进行融合,得到融合结果(质心侧偏角、横摆角速度和纵向车速)。基于AUKF的信息融合算法如图1所示。
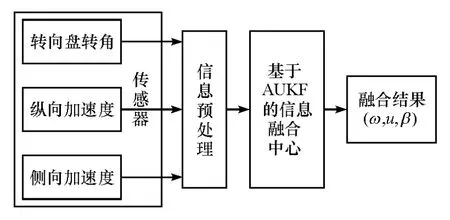
图1 基于AUKF的信息融合算法框图
1.2 自适应无迹卡尔曼滤波理论
经过改进UKF算法得到AUKF算法。UKF算法中事先确定了各种车载传感器的统计特性,如果汽车在行驶过程中受到一定的扰动,必然对传感器产生一定的影响,致使很难准确得到传感器的统计特性,其统计特性会有很大的随机性,即量测噪声的统计特性时变和未知。在这种情况下仍采用UKF算法估计汽车状态,会导致估计误差变大甚至滤波发散问题。
其中,UT变换是UKF的核心内容。在UT变换中,比较常用的Sigma点采样策略有对称采样、单形采样、3阶矩偏度采样和高斯分布4阶矩对称采样等[16]。UT变换的计算量与Sigma采样点的数量有关,常用的对称采样策略的Sigma采样点数为L=2n+1,为了进一步提高系统的实时性,可以采用单形采样,其Sigma采样点数为L=n+2。单形采样策略有两种分别是最小偏度单形采样和超球体单行采样。最小偏度单形采样策略不仅有采样点数最少、计算量最小的优点,而且精度较高[17]。因此,本文中利用UKF算法的新息序列,设计了一种能够对量测噪声统计特性进行估计的自适应无迹卡尔曼滤波(AUKF)算法,实现量测噪声统计特性的在线估计,提高了UKF的自适应能力,避免了在量测噪声统计特性时变或未知情况下UKF状态估计精度下降甚至发散问题。状态估计对于多传感器信息融合系统的意义在于对目标过去的状态进行平滑,对现在的状态做出估计,同时对未来状态做出预测[18]。在已知融合目标与融合结果的相对确切的数学模型的基础上,本文中利用AUKF滤波理论作为信息融合技术的载体,建立信息融合算法。
2 基于信息融合算法的AUKF汽车状态估计
2.1 汽车动力学模型
车辆模型采用包括横摆、纵向和侧向的3自由度非线性车辆模型,车辆模型如图2所示。其动力学方程为
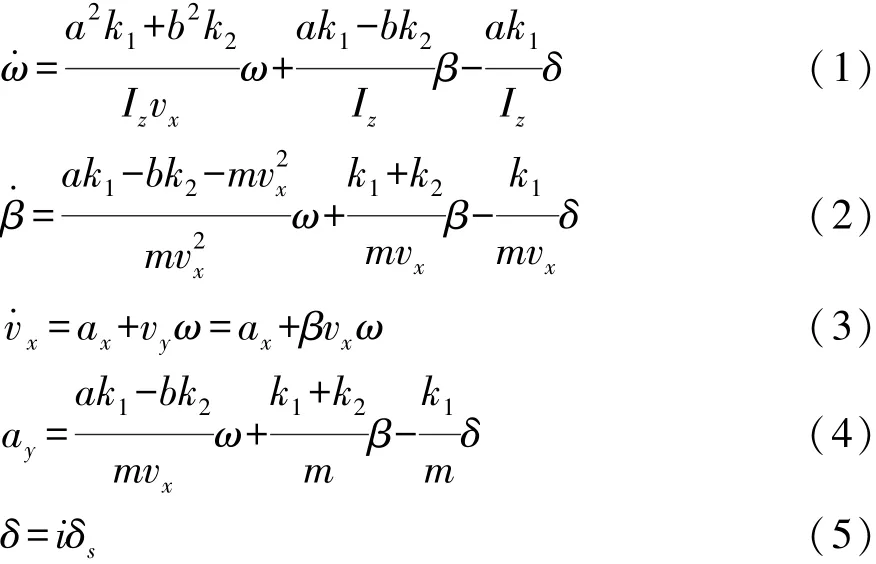
式中:a为前轴到质心的距离;b为后轴到质心的距离;k1,k2分别为前、后轮侧偏刚度;Iz为整车对z轴的转动惯量;m为整车质量;vx为纵向车速;vy为侧向车速;ω为横摆角速度;β为质心侧偏角;ax为纵向加速度;ay为侧向加速度;δ为转向盘转角;δs为前轮转角;i为转向盘到前轮的角传动比。式(1)~式(3)为状态方程,式(4)为观测方程。
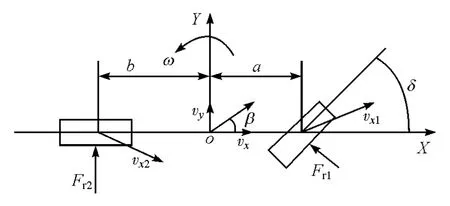
图2 3自由度车辆动力学模型
2.2 AUKF融合算法及应用
2.2.1 量测噪声统计估计
由式(1)~式(4)可得离散的非线性系统模型为
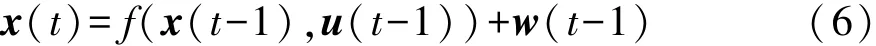

式中:x为状态变量,x(t)= [ω,β,u]T;y为观测量,y(t)=[ay];u为输入变量,u(t)= [δ,ax];w(t-1)为过程噪声,是均值为零、方差为Qt的高斯白噪声序列;v(t)为测量噪声与过程噪声相互独立,是均值为零、方差为Rt的高斯白噪声,且Rt时变和未知。式(6)为状态方程,式(7)为观测方程。
定义量测的新息序列为

新息序列的实时估计协方差为
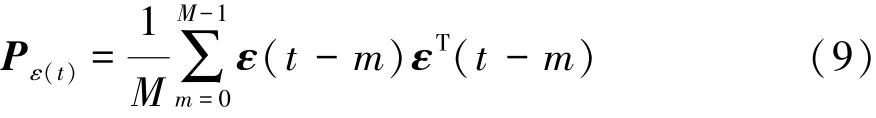
式中M为开窗法中开窗大小[19]。
由此可得量测噪声协方差阵Rt的实时估计值为
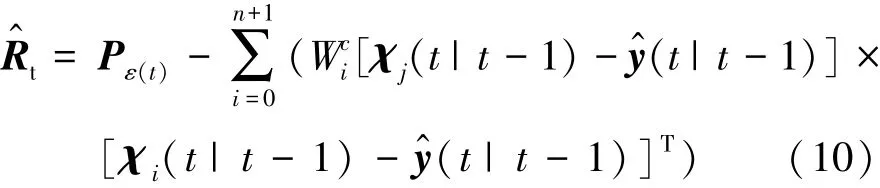
2.2.2 最小偏度单形采样策略
n维最小偏度单形采样策略[20]如下。
(1)首先选取初始权值W0,并且0≤W0≤1。
(2)Sigma点权值计算公式为
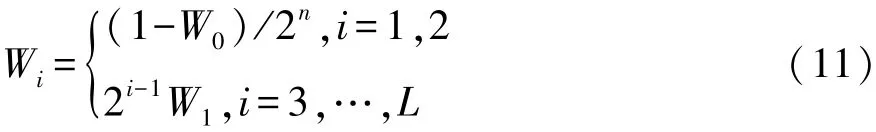
(3)迭代初始向量(对应1维时的采样点)。

(4)对于输入维数为 j=2,…,n时,迭代公式为
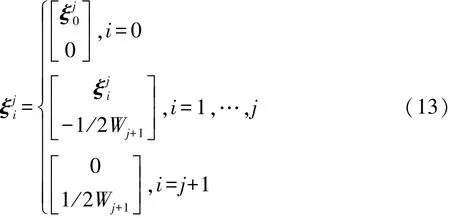
(5)对所生成的Sigma点集中,加入x均值与协方差阵信息。

式中Pxx为x与x之间的协方差矩阵。
(6)均值与方差权值系数为
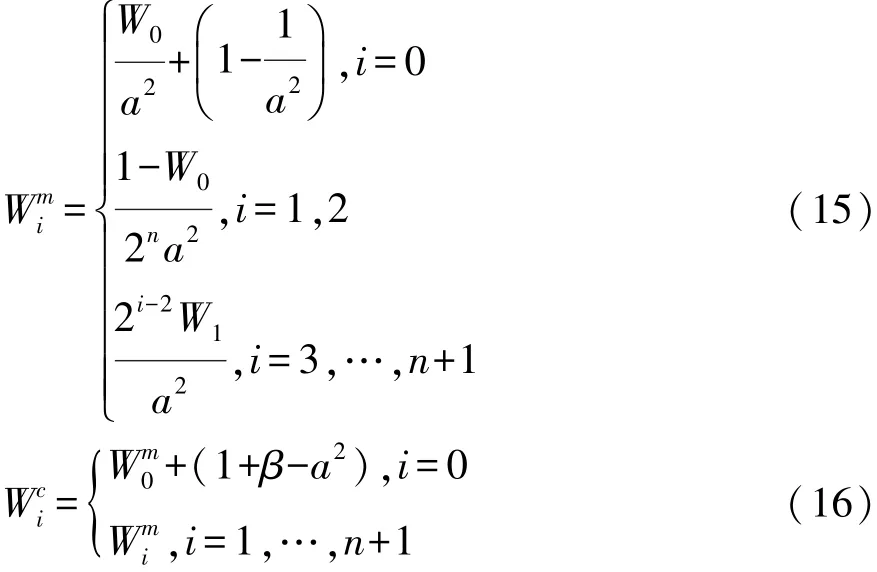
式中:a为取值较小的大于零的比例缩放因子,可在区间[1×10-4,1]取值;β为用于引入随机变数x的分布的先验信息,若其分布服从高斯分布,则β=2最优[21]。
2.2.3 AUKF融合算法流程
以UT变换为基础,利用最小偏度单形采样策略和式(8)~式(10)自适应调整量测噪声公式,对UKF进行优化改进。AUKF算法流程如下。
(1)初始化
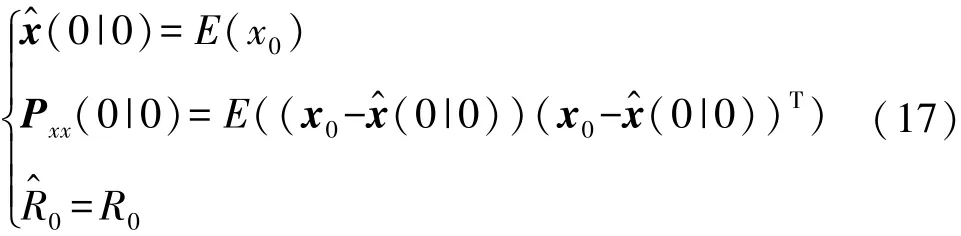
(2)进行改进后的UT变换,计算Sigma点。
(3)时间更新阶段。将由第2步计算得到的Sigma点利用非线性状态方程最终计算出状态预测值及误差协方差阵。
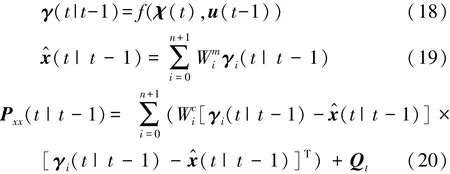
接着,用 x^(t|t-1) 和 Pxx(t|t-1) 分别代替x^(0|0)和 Pxx(0 |0),返回步骤(2)重新计算 Sigma点。通过非线性测量函数传播为χi(k|k-1),因此可得到输出预测和误差协方差阵。
(4)量测更新
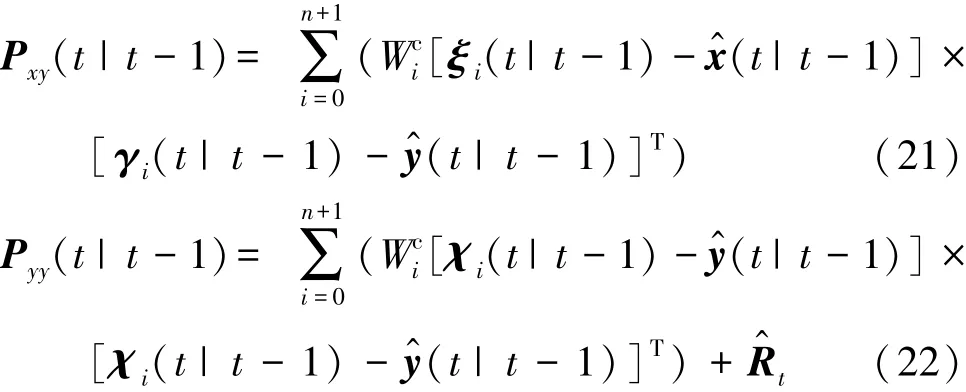
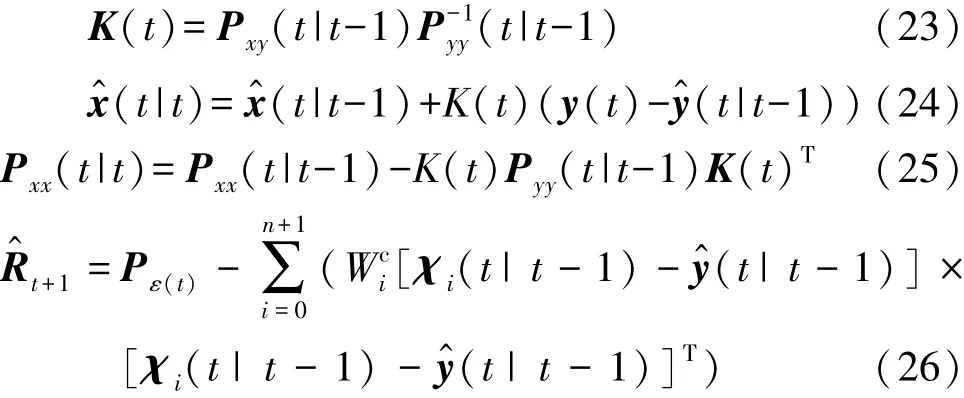
式中:Pxy和Pyy分别为x与y和y与y之间的协方差矩阵;K为卡尔曼滤波增益。
3 仿真与试验验证
3.1 仿真验证
为了验证上述融合算法的有效性,采用CarSim与Matlab/Simulink联合仿真,通过与常用的UKF算法作对比,验证本算法有效性。仿真过程所采用的某车型参数如表1所示。为了模拟极限工况下汽车的操纵性,选用工况为急剧双移线。在CarSim中将路面附着系数设置为0.5,试验车速设置为80km/h,采样时间为0.01s。基于AUKF的车辆状态估计融合中心通过对纵向加速度、侧向加速度和转向盘转角传感器信号的信息融合,对汽车行驶过程中的横摆角速度、质心侧偏角和纵向车速进行实时准确估计,估计值可用于车辆主动安全控制系统。CarSim与Simulink联合仿真原理图如图3所示。
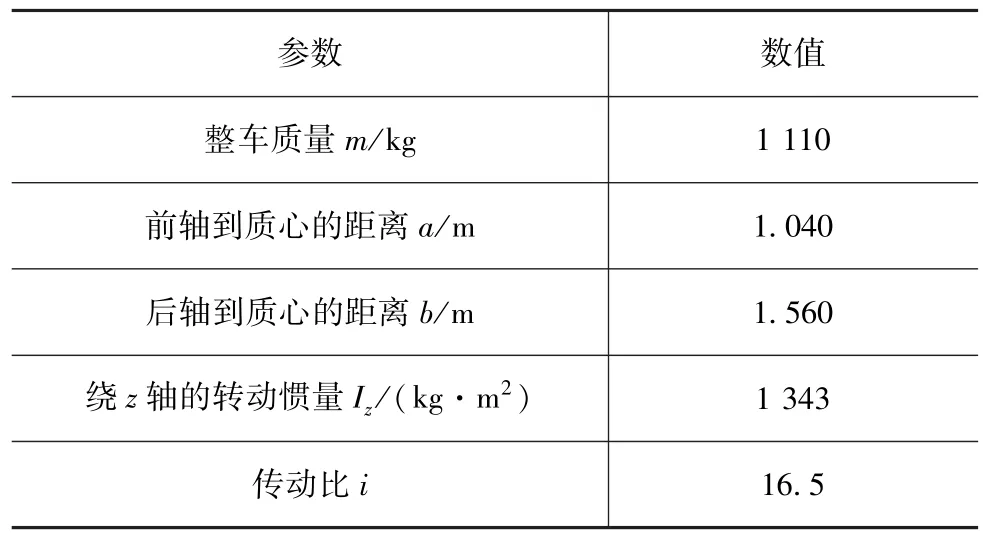
表1 车辆参数
图3 CarSim与Simulink联合仿真原理图
选用急剧双移线工况,在此工况下的汽车行驶路径如图4所示。图5为仿真车辆的转向盘转角、纵向加速度和侧向加速度信号。急剧双移线工况中由UKF和AUKF算法估计的汽车纵向速度、横摆角速度和质心侧偏角的估计值如图6~图8所示。
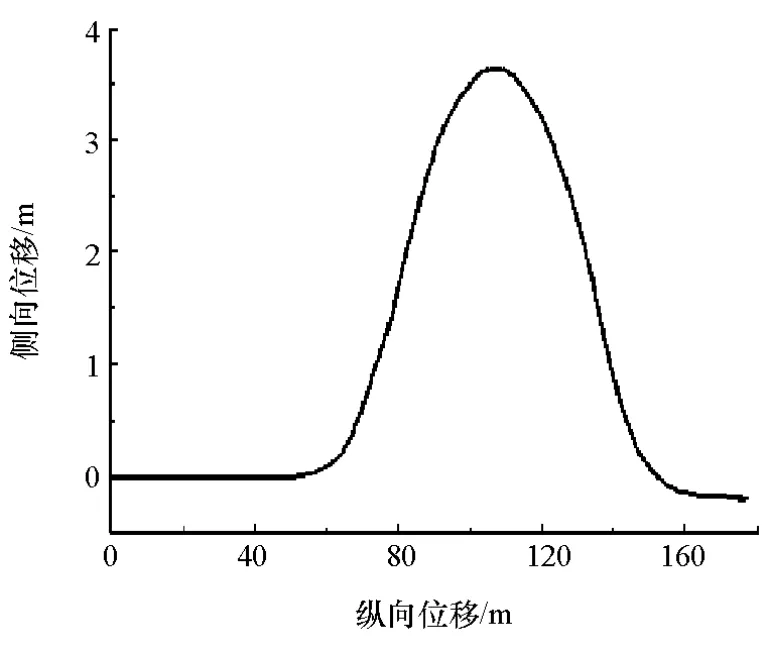
图4 汽车行驶路径
从仿真结果可知,在系统受到外界干扰后,利用UKF算法估计的汽车纵向车速、质心侧偏角和横摆角速度结果与真实值相比会出现较大偏差,尤其是在峰值的地方。而AUKF融合算法能够在线估计噪声的统计特性,利用UKF算法的新息序列对噪声协方差进行调整。相比于单纯的UKF算法,AUKF融合算法能提高估计精度,降低噪声的干扰。
统计计算出参数估计值相对于CarSim仿真结果值的平均绝对误差(MAE)和均方根误差(RMSE)对UKF和AUKF这两种算法的估计精度进行定量比较,表2列出了纵向速度、质心侧偏角和横摆角速度的MAE和RMSE指标。
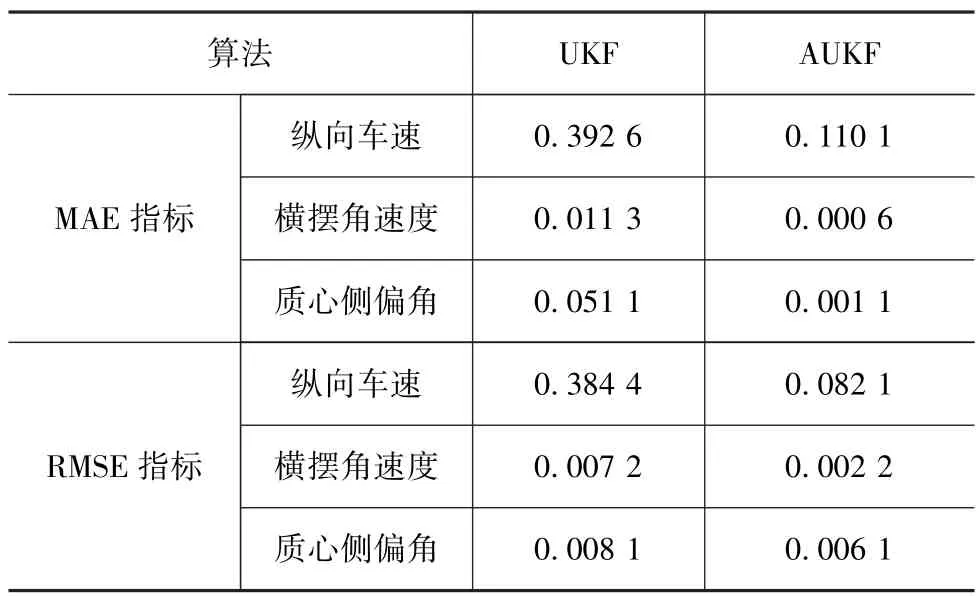
表2 UKF和AUKF的MAE和RMSE指标
从表2可以看出,基于AUKF融合算法估计的纵向车速、横摆角速度和质心侧偏角的 MAE和RMSE指标比UKF小,MAE和RMSE指标定量地反映出了AUKF具有更高的估计精度。
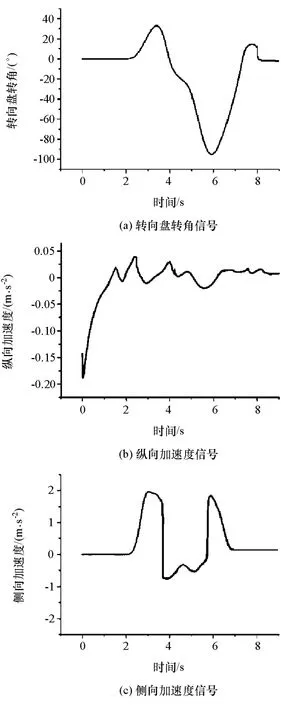
图5 仿真车辆传感器信号
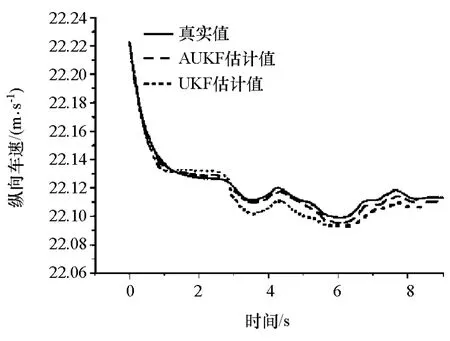
图6 纵向车速估计
3.2 实车验证
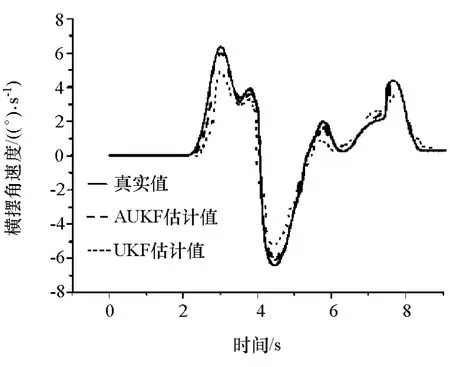
图7 横摆角速度估计
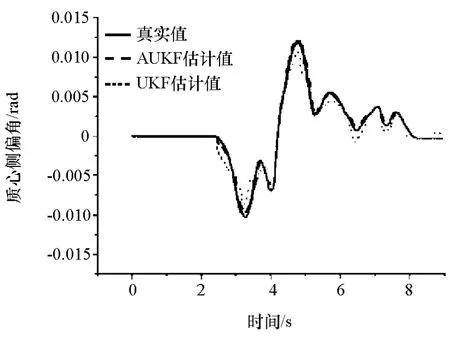
图8 质心侧偏角估计
为了验证提出的车辆状态估计算法的准确性,对某车型轿车进行了在GB/T6323—2014标准的蛇行工况下的实车试验。试验车上安装了陀螺仪、加速度传感器和转向盘转角传感器等,用来采集纵向加速度、侧向加速度和转向盘转角信号。车速为45km/h,采样时间为0.01s,路面附着系数为0.5。
用于模拟道路工况的实车试验平台及其试验系统如图9和图10所示。试验平台监控系统用来记录保存汽车加速度、转向盘转角等信息。CAN总线用来采集上述所有传感器信号和控制信号。快速原型是一套基于产品ECU和Matlab/Simulink的控制系统开发的软硬件平台[22],基于快速原型实现对整车的控制。

图9 实车试验平台
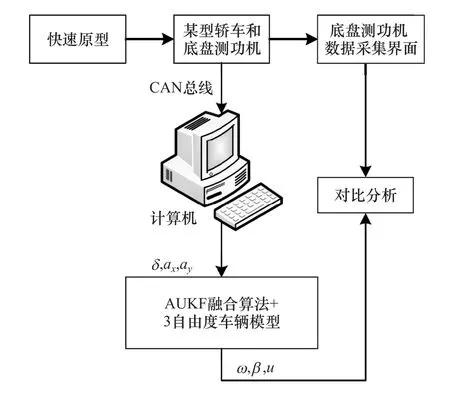
图10 基于实车试验平台的道路模拟试验系统
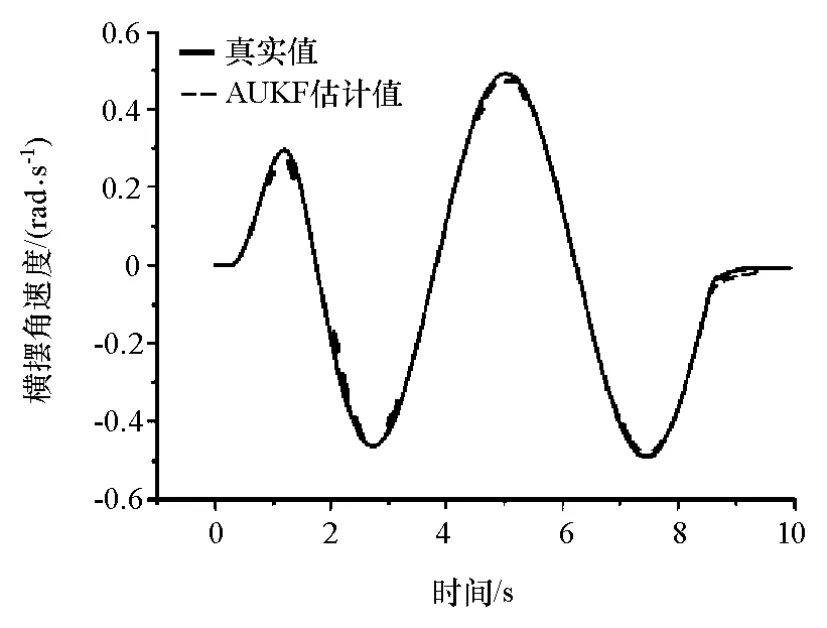
图11 横摆角速度估计值与试验值对比
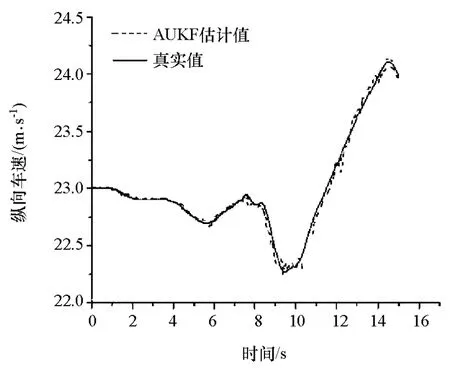
图12 纵向车速估计值与试验值对比
图11 ~图13所示为横摆角速度、纵向车速、质心侧偏角这3个状态量的AUKF估计值与实车试验值的比较。通过分析上述3个状态参数的估计值与试验测量值的对比曲线,可以看出,估计值与试验值虽然存在着一定的偏差,但是在总体上均保持着较高的一致性。因此,本文中在基于较高精度车辆模型的前提下,采用AUKF算法得到的估计结果达到了较高的精度。此外,在试验车进行测试时,传感器安装位置的偏差也是估计值与测试值产生误差的一个重要因素。
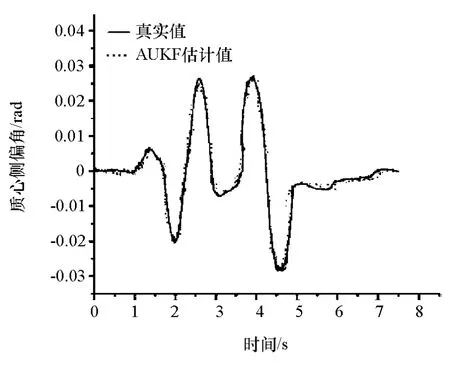
图13 质心侧偏角估计值与试验值对比
4 结论
本文中基于AUKF理论建立了信息融合算法,融合转向盘转角、纵向加速度、侧向加速度信息,给出车辆状态最小方差意义下的估计。经试验验证,该算法对车辆状态的估计表现出良好的性能。
(1)提出基于信息融合的AUKF状态估计算法,对汽车行驶过程中状态参数进行估计。AUKF算法中,由于在UKF算法基础上加入新息序列,利用最小偏度单形采样策略和量测噪声自适应调整,可降低系统过程噪声和量测噪声对估计结果的影响,大大减小估计结果与真实值之间的误差,使得到的估计值精度更高。
(2)利用多个低成本传感器采集的信号,在信息融合的基础上,把多源信息进行融合,达到了以较低成本的传感器对较易测量的转向盘转角、纵侧向加速度等对多种参数进行估计。此方法更具有普及性。
(3)仿真和实车试验表明,相比于单纯的UKF算法,AUKF融合算法的估计结果与试验真实值有更好的一致性,具有更高精度和抗干扰性。对工程领域有很好的价值意义。此外,由于试验条件和工作量的原因,本文中试验工况不具备广泛性,后续工作将在更多的工况下进行。
