基于模式切换预估算法的DM-EV瞬时能耗最小控制策略∗

林歆悠，王黎明，翟柳清

(1.福州大学机械工程及自动化学院，福州 350002； 2.福建省高端装备制造协同创新中心，福州 350002)

前言

近年来,节能环保型电动汽车越来越受到大众的关注,但由于其有限的续驶里程且电池技术尚未得到突破性进展,因此未能得到广泛使用[1-2]。基于此,提高能量利用率是目前针对这一问题采取的常见措施,具体可通过优化控制策略及采用多模式双电机耦合驱动构型等方法来提高能量利用率[3]。

通过优化或采取合理的控制策略能够使多模式双电机耦合驱动构型电动汽车在稳定性、动力性、经济性等方面得到更大提升。张利鹏等[4]采用两侧分布式驱动系统的双电机动力耦合控制,不仅能够抑制驱动力矩波动,而且起到增强车辆高速稳定性的作用。杨胜兵[5]提出基于分时控制的双电机驱动控制策略,通过与单电机驱动系统对比仿真,验证了其在动力性方面的提升。ZHANG S等[6]应用动态规划算法结合最优控制策略来改进双电机耦合驱动构型的控制策略,通过仿真分析得出此算法能够有效降低系统能量损耗。TSENG S K等[7]研究了一种新型双电机驱动系统及其控制策略,可实现两个电机在额定转速范围内输出最大转矩,在额定转速外,通过能量的重新分配来让驱动系统继续以高转矩输出。

多模式双电机耦合驱动构型由于同时具备单电机驱动及双电机驱动模式,既能够实现高转矩及高转速的输出,又可改善电机工作效率从而提高系统的能量利用率[8-9]。张运昌[10]提出的动力耦合装置是通过3个离合器与1个锁止器的接合与分离来实现4种工作模式,利用电机最小需求功率法制定了模式识别规则及耦合模式下的动力分配规则。曾剑峰[11]根据控制电机的启停、制动器的接合与分离以及同步器接合套的位置来实现4种工作模式,并在模式切换子过程中提出电机转矩协调控制方法。胡明辉等[12]通过控制电机的开启与关闭、制动器的接合与分离以及同步器的位置切换实现4种工作模式,并进行耦合模式下的转矩协调控制算法的研究,以确保模式切换过程中动力传递的连续性和平稳性。

由于多模式耦合驱动构型能够使电机更多地工作于高效区[13],因此本文中以多模式耦合驱动构型电动汽车作为研究对象,首先分析该系统构型及工作模式,其次制定了基于模式切换预估算法的DMEV瞬时能耗最小控制策略,最后建立仿真模型及搭建台架试验平台,通过仿真及台架试验对该控制策略的有效性及驱动系统的性能特性进行试验分析。

1 系统构型及工作模式分析

本文中所研究的多模式双电机耦合驱动系统构型如图1所示,此系统可以实现电机M1单独驱动模式(SM1)、电机M2单独驱动模式(SM2)、双电机转矩耦合驱动模式(TC)和双电机转速耦合驱动模式(SC)。

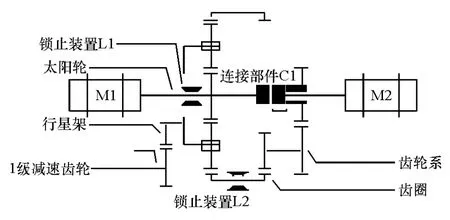
图1 多模式双电机耦合驱动结构

各驱动模式与部件的对应关系如表1所示。

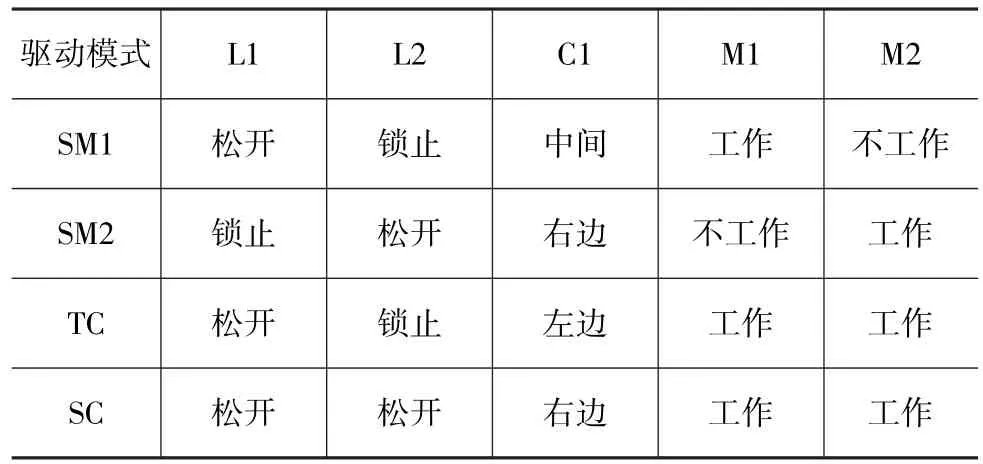
表1 驱动模式与部件对应关系

SM1模式时,M1驱动太阳轮,齿圈被锁止；SM2模式时,M2驱动行星架,太阳轮被锁止；TC模式时,M1与M2共同驱动太阳轮,齿圈被锁止；SC模式下,M1与M2分别连接太阳轮和齿圈。所有模式下,动力从行星架输出。

当驱动系统处于单电机驱动模式时,其动力源仅为一个电机,不存在动力分配问题；而处于双电机耦合驱动时,动力由两个电机共同提供,需要对两个电机动力进行分配,具体为SC模式和TC模式,这里以SC模式为例进行分析。

SC模式下,消耗的电机系统功率可表示为

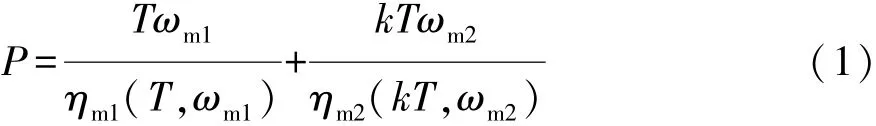
式中：ηm1,ηm2为两电机的效率；ωm1,ωm2为两电机的角速度；T为M1转矩；k为变量。电机角速度、转矩与需求输出的角速度、转矩关系如式(2)所示。

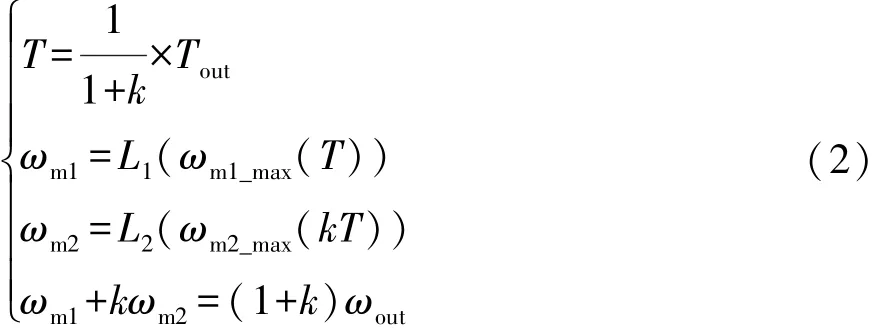
式中：ωm1_max(T),ωm2_max(kT)分别为电机M1,M2在当前转矩下的最大角速度；L1,L2分别为两电机当前转矩下最大角速度的分量；ωout,Tout分别为需求输出的角速度与转矩。则当前消耗功率可以看成固定转速以及成线性约束关系的转矩下实现最小工作功率点的选择,而影响此功率的因素为两个电机的效率。

由以上分析即可得到SC模式下电机最优转速分配,如图2所示,可根据在不同耦合转矩及不同耦合转速下通过查表插值获得两电机转速,从而方便在台架试验中直接运用于实际控制器的开发。

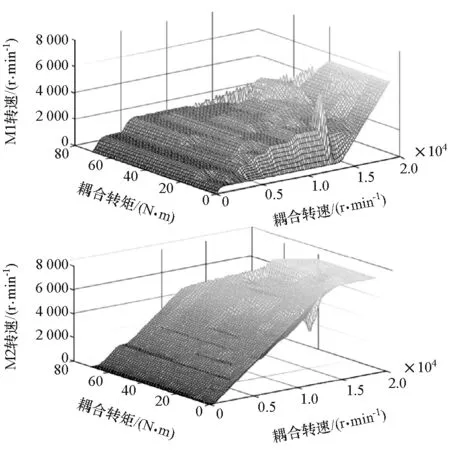
图2 SC模式下电机最优转速分配

2 基于模式切换预估算法的瞬时能耗最小控制策略

2.1 制定模式切换预估算法

图3为模式切换有预估算法和无预估算法下驱动系统的模式切换过程。由图可见,在t1时刻前模式1为能耗最小的驱动模式,之后模式2为最优。在理想控制策略下,驱动模式会在t1时刻进行切换,而在不含预估算法控制中,会在t1时刻开始识别出此时应该切换到模式2,并在t2时刻进行切换,则会多出图3(b)所示的一部分能量消耗区域。

由于该驱动系统不同模式之间切换并不是瞬间完成的,若要在理想的模式切换时刻t1进行模式切换,则需要在此时刻之前的t0时刻就进行模式切换准备,即计算出模式切换时间长度。

模式切换时间长度主要为电机调节时间tmotor-coup与离合器运动时间ttrans-coup,其中电机调节时间由电机调速和转矩调节时间组成。离合器的运动时间一般看成固定值C1。则提前预测时间的计算如下：

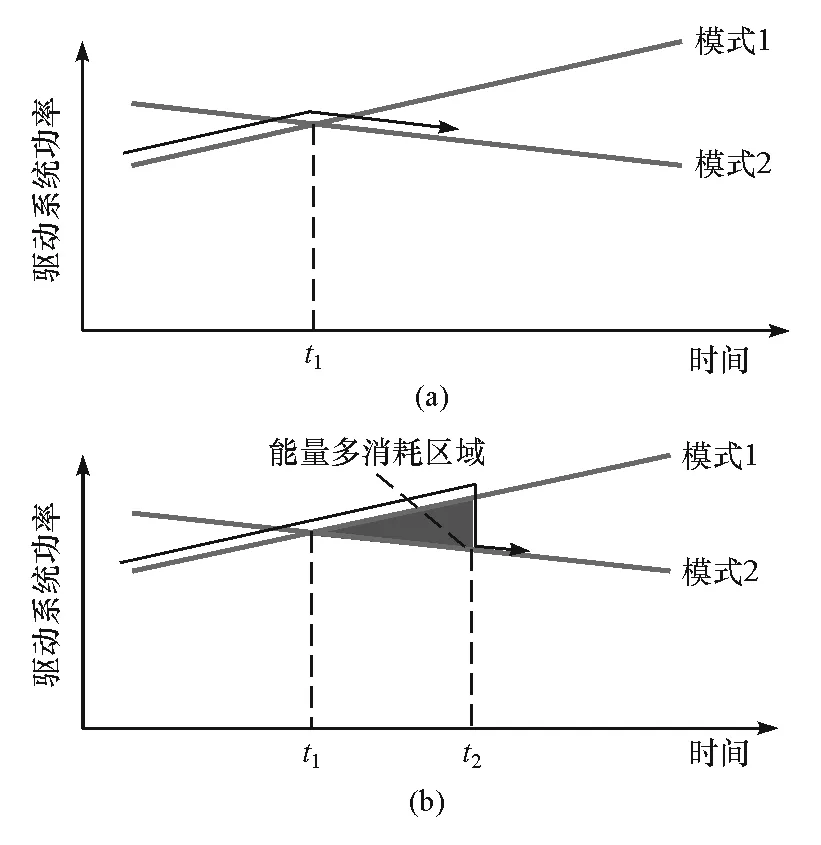
图3 有预估算法与无预估算法模式切换对比图

式中：ωt0,ωt1分别为t0,t1时刻电机转速；λ为线性关系量；tdelay-torque为转矩响应延迟时间。

设在t0时刻踏板的行程为θ0,行程变化率为基础转矩与辅助转矩的计算与踏板关系简写为f1与f2,将近似看成恒定。则任一t时刻需求转矩计算公式为

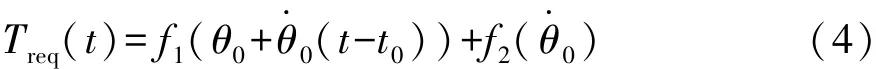
t时刻的汽车动力学方程为

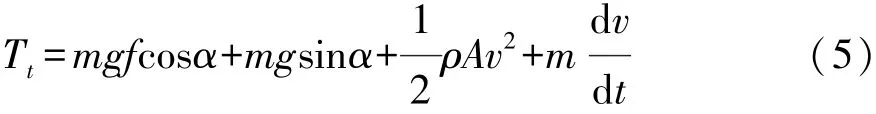
设t时刻输出角速度为ωt,传动比为i,则

由式(3)～式(6)可算出任意t时刻系统的输出角加速度为

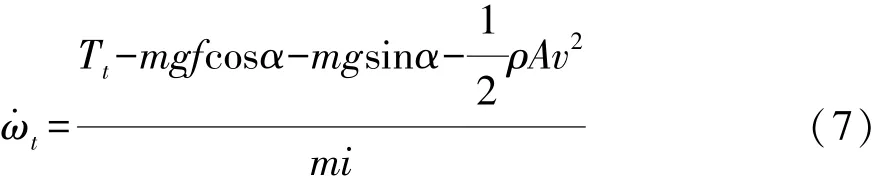
则在t1时刻驱动系统输出角速度为

由上可得到t1时刻电机输出角速度与转矩为

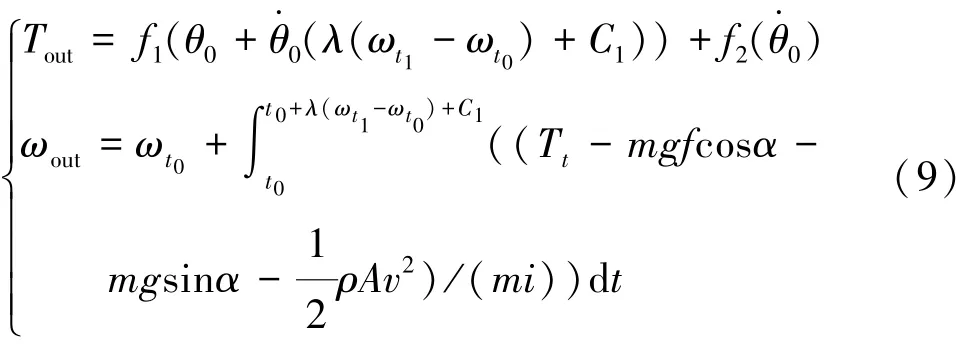
将t1时刻电机的角速度与转矩带入式(3)中即可求出模式切换时间长度。

2.2 构建基于模式切换预估算法的瞬时能耗最小控制策略

基于瞬时优化的控制策略可通过当前的工况和预测接下来的某段工况来选择此时刻最优的模式,而且可以针对不同工况来指定不同的优化目标[14-15]。本文中所研究的驱动系统是通过汽车当前运行工况结合预估算法来估算出模式切换时间长度从而在最适合的时刻进行模式切换,因此选用基于模式切换预估算法的瞬时能耗最小控制策略。

本文中选择了系统最小瞬时能耗为优化目标,即

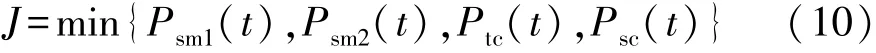
式中：Psm1(t),Psm2(t),Ptc(t),Psc(t)分别为其对应驱动模式下的系统消耗功率；t为循环周期1s内所运行的某一时刻。

4种驱动模式下的系统能耗计算如下：

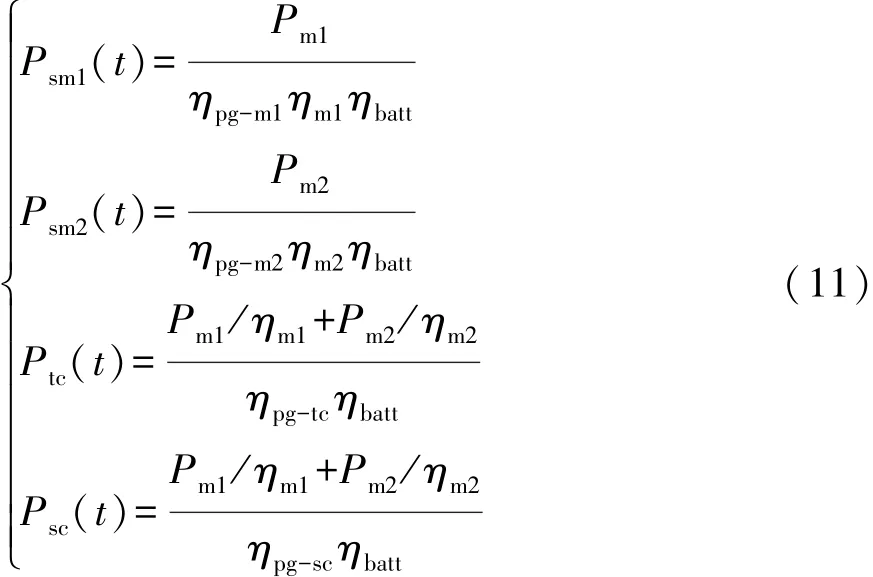
式中：Pm1,Pm2分别为电机M1,M2的输出功率；ηm1,ηm2分别为电机 M1,M2的工作效率；ηpg-m1,ηpg-m2,ηpg-tc,ηpg-sc为耦合装置在对应驱动模式下的传动效率。

在此过程中的部件约束为

其它约束条件如下：(1)汽车处于紧急制动情况下时,为保证安全,不允许模式切换；(2)两次模式切换的时间间隔不小于40s。

图4为驱动模式切换控制流程图。设置汽车起动驱动系统为SM1模式,原因是SM1模式效率较高。在汽车行驶过程中,在循环周期1s内计算一次当前工况转矩Tnow与角速度ωnow是否满足最大转矩Tmax和最大角速度ωmax的需求,若满足则计算得出使目标函数J最小所对应的模式mode_Jmin,之后判断此刻时间tnow与上一次模式切换时间tlast的间隔及汽车的减速度adec,若间隔时间大于40s,且减速度小于制动识别阈值-1.5m/s2,则切换到目标模式,否则保持当前模式。如果进行了模式切换,则将此刻时间作为tlast,至此完成一个循环。如果汽车进入停车状态,则将驱动模式切换回SM1模式。

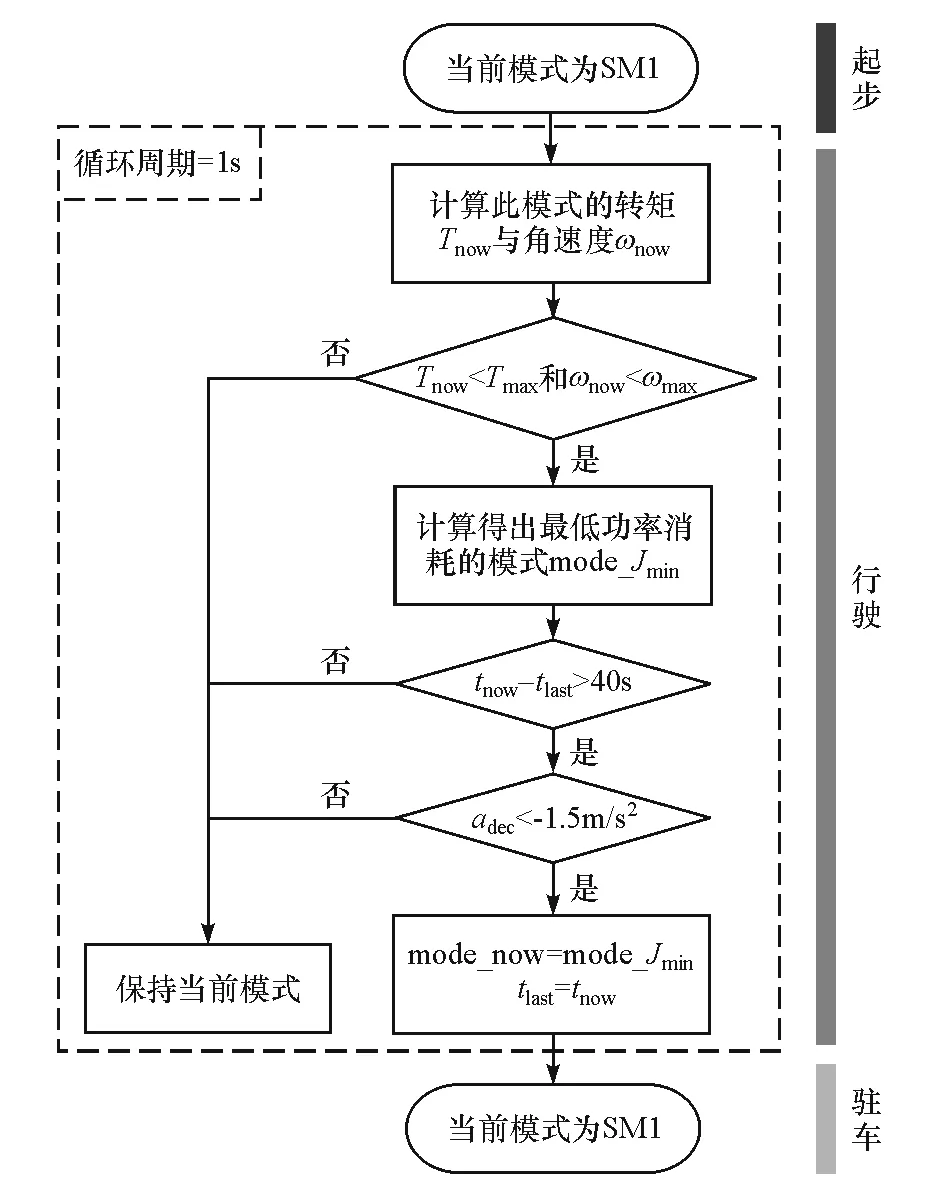
图4 驱动模式控制策略流程图

综上所述,由瞬时能耗最小控制策略计算得出每一时刻能耗最小对应的模式,结合模式切换预估算法,通过提前进行模式切换准备,从而实现在理想的模式切换时刻t1进行模式切换,减少多余的能量损耗,以达到控制策略优化的目的。

3 仿真分析与台架试验验证

3.1 典型工况下仿真试验分析

本文中利用Matlab/Simulink仿真平台,建立后向式整车仿真模型,让此驱动系统在代表城市拥堵工况、城市一般工况、高速公路工况的 NYCC,UDDS,HWFET 3个典型工况下进行仿真试验分析。

3.1.1 不同驱动模式下能耗效率对比分析

各驱动模式的能耗效率为

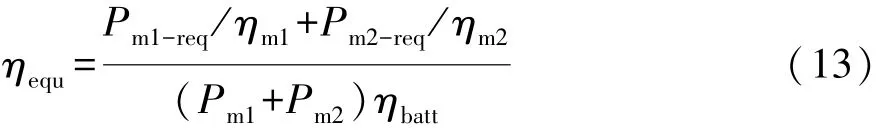
式中：Pm1-req,Pm2-req分别为电机M1,M2的需求输出功率；ηm1,ηm2分别为电机 M1,M2的工作效率；ηbatt为电池的效率。

通过仿真,3种典型工况下系统的能耗效率变化如图5～图7所示。在NYCC工况下,由于车速低故SC模式的效率较低。在UDDS工况下,汽车大多处于中高速运行,故SM2与SC模式处于较高效率的情况较多。HWFET工况则代表着高速行驶工况,因而SC模式成为了主要的高效运行模式。

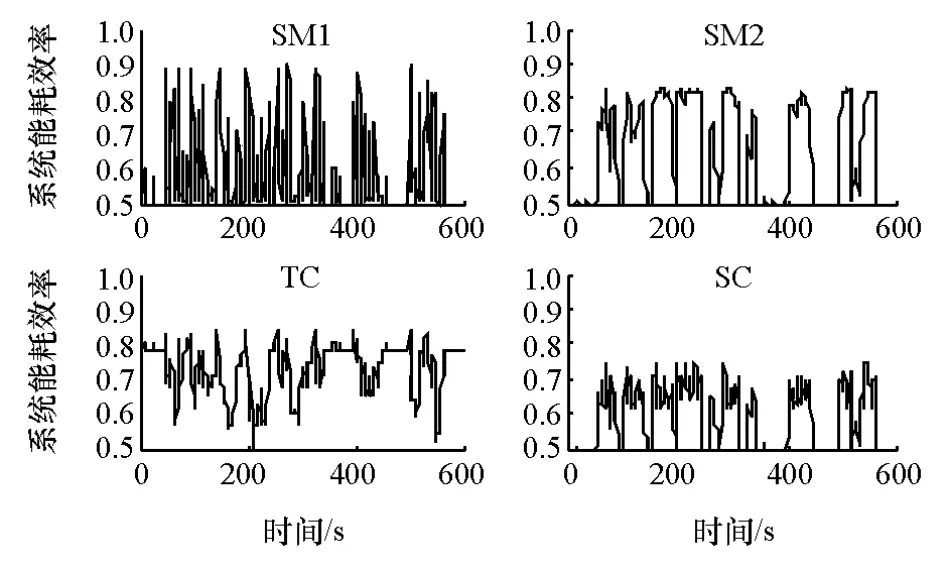
图5 NYCC工况下各驱动模式系统能耗效率

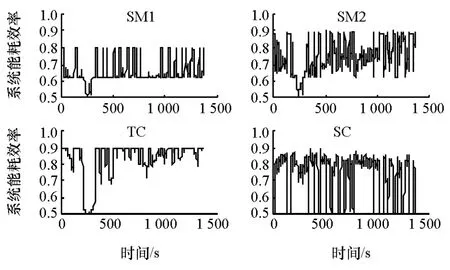
图6 UDDS工况下系统能耗效率

在以上仿真结果基础上,结合所研究的模式控制策略,可得到基于瞬时能耗最优的驱动模式选择结果,如图8所示。

3.1.2 模式切换预估算法对能耗的影响分析

为验证所研究的预估算法的节能特性,3种典型工况下的有预估算法与无预估算法的对比结果如图9所示。仿真结果数据显示,在NYCC,UDDS,HWFET工况下,通过模式切换预估算法使能量利用率分别提高了2.2%,3.6%,1.7%。

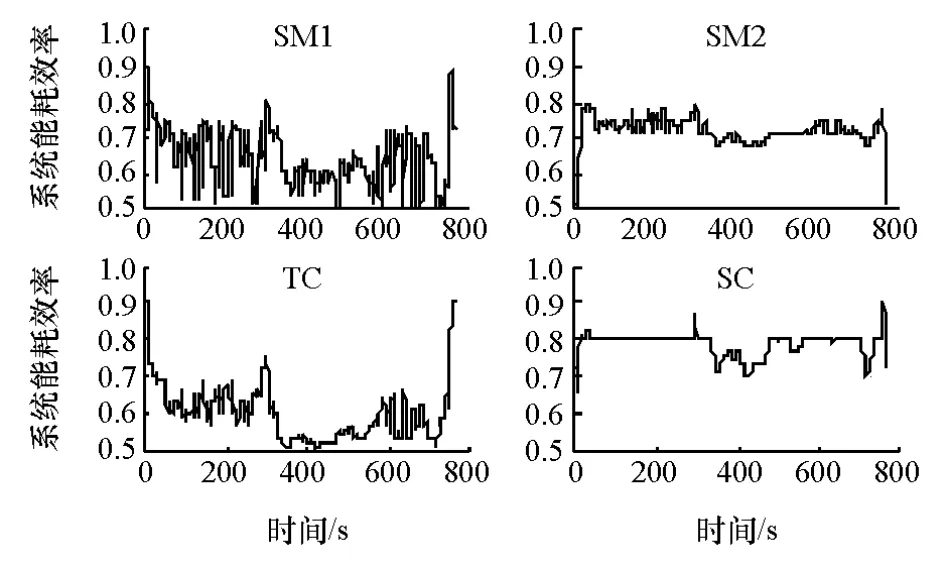
图7 HWFET工况下系统能耗效率

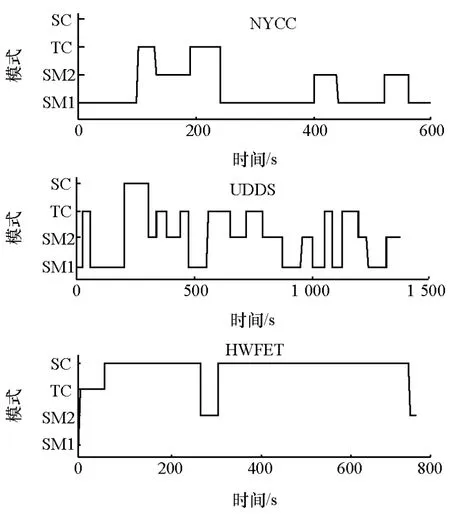
图8 典型循环工况下的模式选择图

3.2 台架试验验证

为验证所研究的双电机系统比单电机系统在性能上具有更大的优势,因此搭建了双电机耦合驱动系统台架试验平台,图10所示为台架试验结构示意图,图11为台架试验实物图,包括试验操作台、CAN总线、能量管理控制器、电机控制器、NI数据采集系统、电池组、电机M1和M2等。

该台架的驱动系统内部外部均采用CAN总线进行数据通信,将波特率设置为250kbps,采用J1939应用协议。该台架的主控制器选用飞思卡尔MC9S12EQ512汽车级微处理器来作为主控芯片。而上位机数据采集系统软件部分使用NI公司的LabVIEW软件来设计,硬件部分包括PXI数据采集卡、传感器和计算机。

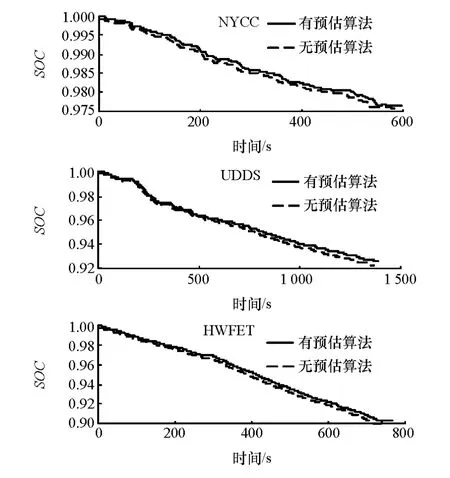
图9 模式切换预估算法对SOC的影响

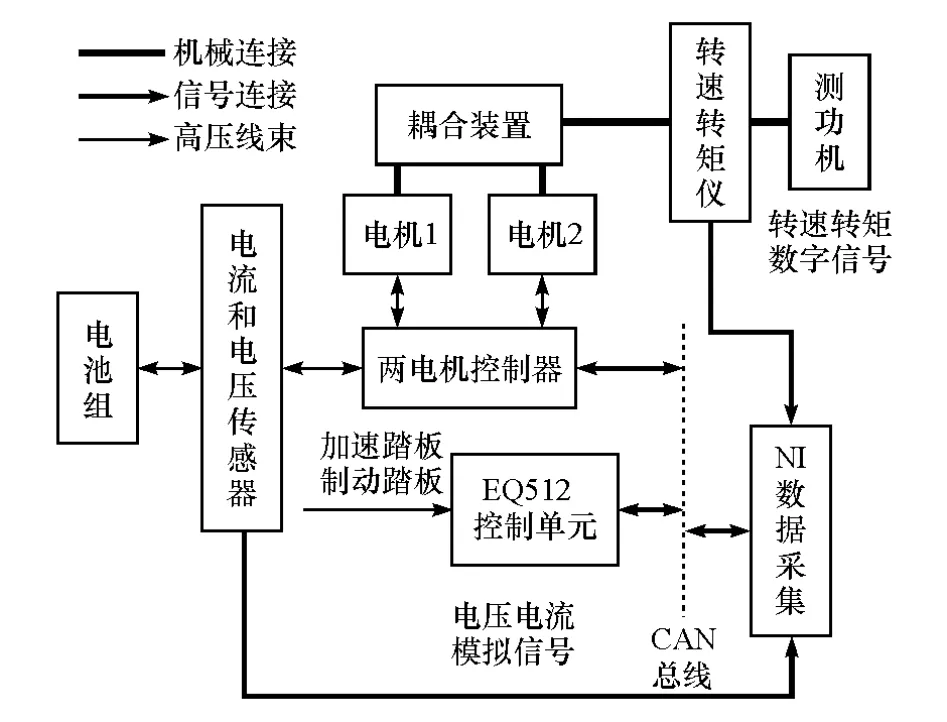
图10 台架试验结构示意图

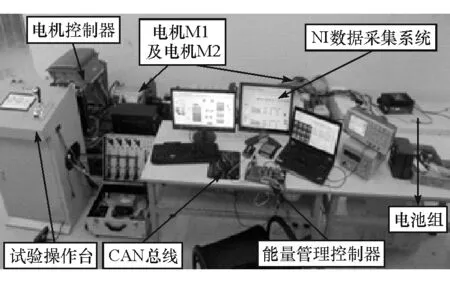
图11 台架试验实物图

利用搭建的双电机台架试验平台测得3种工况下电池SOC的变化图,再将双电机用与之总输出性能相近的峰值功率为95kW,峰值转矩为220N·m、最大转速为9 000和额定转速为5 000r/min的单电机替换,测得3种工况下SOC的变化图作为对比参考,如图12所示。系统台架试验结果表明,在3种工况下所研究的双电机系统比单电机系统能量利用率分别提高了14.2%,11.5%和10.1%。

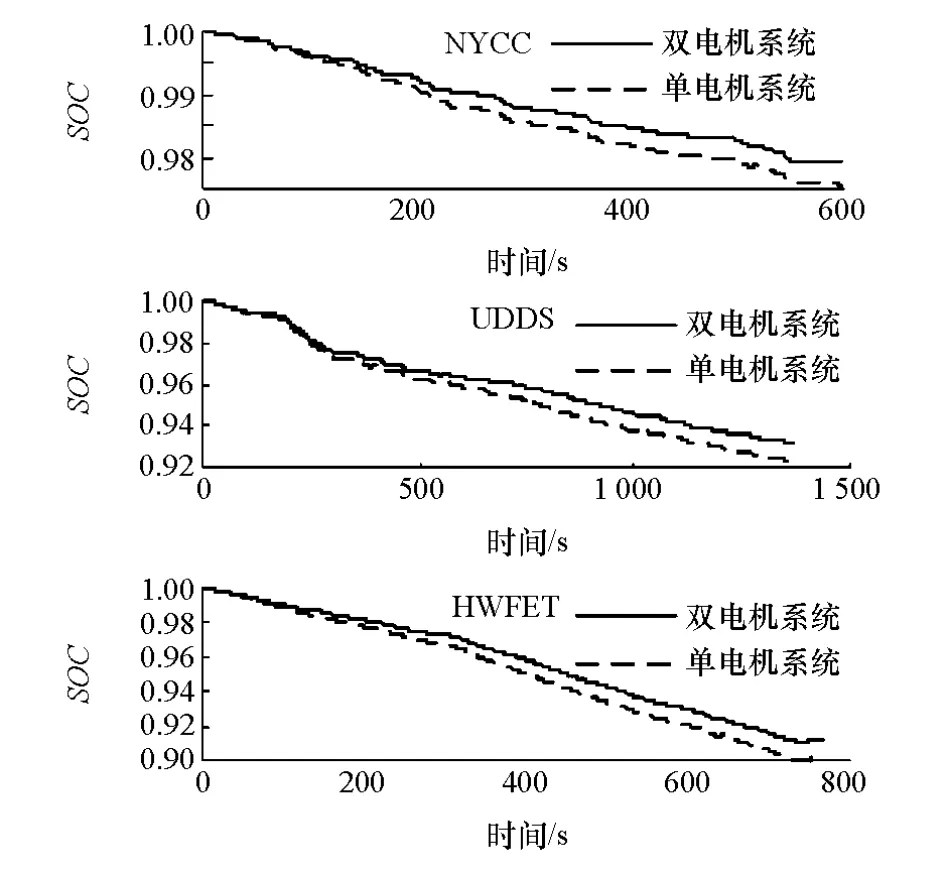
图12 单/双电机驱动系统SOC对比

4 结论

(1)以一款新型的多模式双电机耦合驱动构型电动汽车为研究对象,制定了基于模式切换预估算法的瞬时能耗最小控制策略,并通过该预估算法计算出模式切换时间长度,以此来优化以瞬时能耗最小为目标的模式切换控制策略。

(2)利用Matlab/Simulink仿真平台建立仿真试验,在城市拥堵工况、城市一般工况和高速公路工况下对各驱动模式能耗效率进行仿真试验分析,得到对应的最优驱动模式,并验证了利用预估算法来优化控制策略可提升系统能量的利用率。利用搭建的双电机耦合驱动系统台架试验平台,通过将所研究的双电机系统与单电机系统在SOC的变化图作为对比,验证了其在节能方面的优势。

(3)综上所述,所研究的驱动构型及制定的控制策略具有一定的可行性和有效性,并且为后续进一步研究双电机耦合驱动系统控制策略奠定了基础。