基于自适应准PR控制器的MMC环流控制策略研究

汪玉凤， 王济东， 佟丽新， 叶 青

(1. 辽宁工程技术大学电气与控制工程学院， 辽宁 葫芦岛 125105；2. 国网辽宁省电力有限公司阜新供电公司， 辽宁 阜新 123000)

1 引言

近些年，模块化多电平变流器(Modular Multilevel Converter，MMC)在高压直流输电、电能质量治理等中高压领域具有显著的竞争优势[1-4]。然而MMC结构中的三相桥臂并联在公共直流侧，而储能部分分布在不同的模块单元中，稳态运行时每个桥臂的电压不可能相同，各桥臂除了负载电流还存在一定的环流。尽管环流的存在不会影响输出电流，但会使桥臂电流发生畸变，增加整个变流器的功率损耗，严重影响MMC的稳定运行[5-8]。因此，如何抑制MMC中的相间环流是MMC开发应用中的一个关键问题。

针对MMC的环流问题诸多文献都进行了研究。文献[9,10]采用适当增加桥臂的电抗来抑制环流，这种方法并不能完全消除环流，而且还会增大系统的体积，提高成本，影响系统的稳定。文献[11]对内部环流机理进行了分析，推导出了环流的二次分量的计算公式，为环流的抑制提供了理论依据。文献[12,13]提出采用比例积分控制器对环流进行抑制，但需要将桥臂环流在旋转坐标系下进行分解，工程实现上较为困难。文献[14]提出了MMC的桥臂环流中不仅有二倍频环流分量，还有四次、六次等偶数次环流分量。文献[15,16]设计了基于PR控制器对环流进行抑制，PR控制器可以实现对特定次谐波进行抑制，但由于PR控制器的局限性，当电网频率波动时对电网的鲁棒性变差，满足不了控制要求。文献[17,18]设计了基于准PR控制器对环流进行抑制，虽然准PR控制器弥补了PR控制器的不足，但是没有考虑其他偶数次环流。

针对MMC的环流问题，提出了一种基于自适应准PR控制的方法，设计一种对系统稳定性影响较小的参数调整规则。此外，按扰动补偿的复合校正的方案对子模块电容电压扰动进行前馈补偿，抑制二倍频环流的同时对其他偶数次环流进行抑制。

2 MMC的拓扑结构

MMC的拓扑结构如图1所示。可以看出，MMC一共有六个桥臂，每个桥臂都由N个子模块(SM)串联一个电感L组成，同相的上、下两个桥臂构成一个相单元。每个子模块都由两个带有反并联二极管的IGBT 串联后再与一个直流储能电容并联构成半H桥。

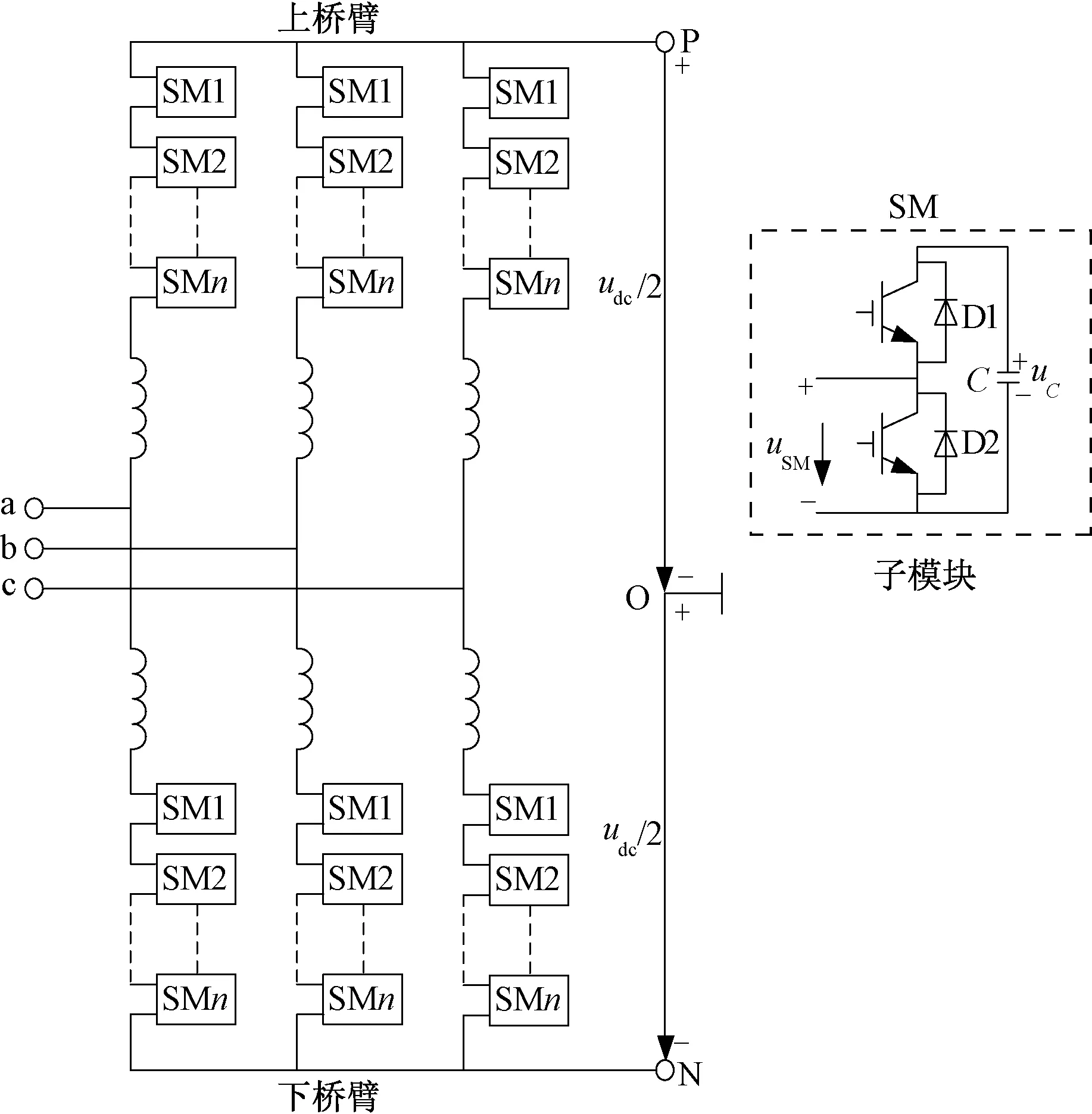
图1 三相MMC拓扑结构图Fig.1 Topology of 3-phase MMC

3 MMC的内部环流分析

图2为MMC单相等效电路。上、下桥臂的N个子模块分别等效为ukP、ukN两个受控电压源，R为桥臂等效电阻，O为直流侧等效中性点，iZk为k相的环流。

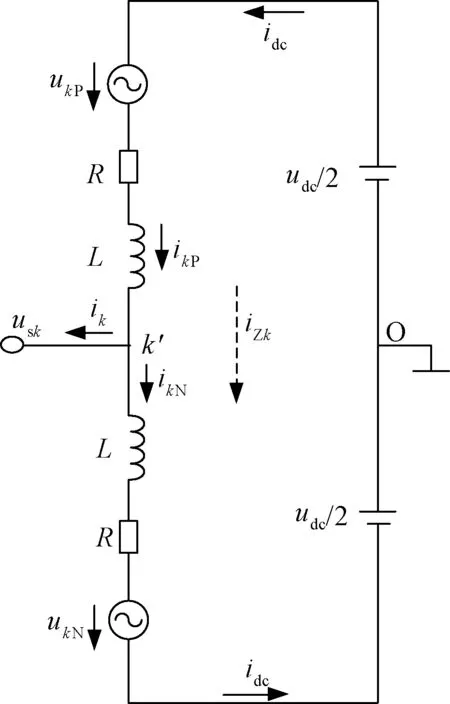
图2 MMC单相等效电路Fig.2 Single phase equivalent circuit of MMC

根据基尔霍夫定律可得：

(1)

根据式(1)得：

(2)

MMC直流侧的公共母线是通过各个桥臂子模块的电容输出有功和无功功率的，其载体是各相的环流iZk，根据能量守恒定律可得：

(3)

由A、B、C三相得：

iaP+ibP+icP=iaN+ibN+icN=idc

(4)

为了简化推导过程假设系统对称，将式(1)代入式(4)可得：

iZa+iZb+iZc=idc

(5)

将式(5)代入式(3)可得：

(6)

以A相为例，假设A相电压、电流为：

usa=Umsinωt

(7)

ia=Imsin(ωt-φ)

(8)

式中，Um、Im分别为输出电压和电流的峰值；ω为输出基波角频率；φ为输出的功率因数角。

以A相为例，由式(6)可得：

φ+cos(2ωt-φ)]

(9)

假设udc稳定。定义电压调制比F，F=2Um/udc，则

φ+cos(2ω-φ)]

(10)

根据式(10)可以得出，MMC各相桥臂的环流由直流分量和二倍频分量组成。其中直流分量是直流侧和交流侧能量交换所引起的，与MMC的工作状态有关，当外部的传输功率一定时，没有办法通过控制的手段进行抑制。

以上分析是在假定各相的子模块直流电压恒定的条件下得到的，而在实际的MMC桥臂中，环流会与子模块电容电压相互影响。二倍频环流导致子模块三倍频电容电压波动；三倍频的电容电压波动反过来又会引起四倍频环流的产生。以此类推，最终可得到环流中主要包含偶数次环流[19]。因此有必要在抑制二倍频环流的同时消除子模块电容电压波动对环流的影响。

4 MMC环流抑制策略

基于第3节的分析可知，桥臂环流可分为自身的二倍频环流和由子模块电容电压扰动所产生的其他偶数次环流。针对桥臂的二倍频环流，提出一种容易实现的自适应准PR控制策略，详细分析控制器中谐振系数对系统的影响，为了能适应负载的变化给出谐振系数的调整规则。同时按扰动补偿的复合控制方法，对子模块电容电压扰动进行前馈补偿以抑制子模块电容电压影响所产生的其他偶数次环流。

4.1 自适应准PR控制器设计

相比于PI控制器，PR控制器能够无误差地跟踪特定频率的交流信号，因此可以抑制MMC桥臂环流中二倍频环流。但是传统的PR控制器稳定性差，而且当电网频率发生波动的情况下，系统的鲁棒性会变差。因此选择控制性能更优的准PR控制器，在保持常规PR控制器高增益的同时，提高了抗电网频率波动的能力。其传递函数为：

(11)

式中，kp为比例系数；kR为谐振系数；ωc为截止频率；ω0为谐振频率。其中ωc影响着系统的带宽和开环增益。设电网频率波动为±0.5Hz，准PR控制器的带宽为ωc/π=1Hz，则ωc=3Hz。由此根据MMC的拓扑结构设计基于自适应准PR控制器的MMC环流抑制结构，如图3所示。

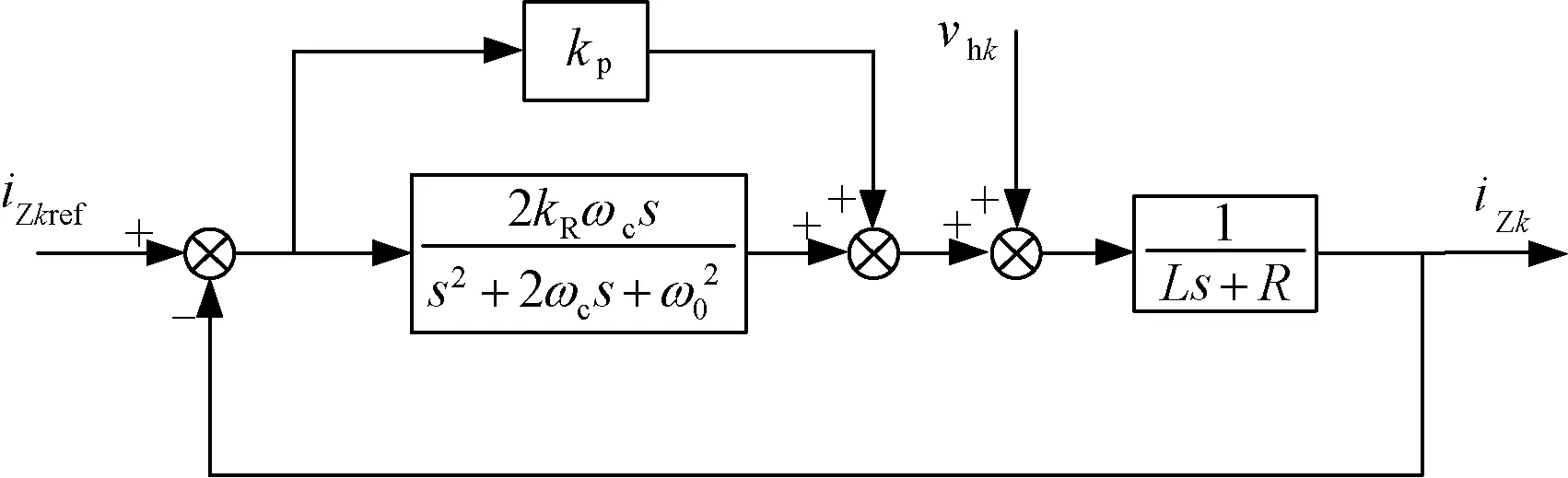
图3 基于准PR环流控制器Fig.3 Circulation controller based on quasi-PR

图3中，L和R为桥臂的等效电抗和电阻，vhk为桥臂子模块电容电压的扰动干扰。根据图3得出系统开环传递函数为：

(12)

与PR控制器不同的是，准PR控制在ω0处的增益不再是无穷大，而是有限的，大小为kp+kR，所以可以通过改变kR的值来使系统获得足够大的增益，kR的设计对于整个控制器至关重要。图4、图5分别为当kp=4时kR=60、kR=200、kR=400对应的开环传递函数的伯德图和根轨迹图。

“重写文学史”最有力的资源与挑战莫过于萨义德“东方学”的影响。萨义德强调，东方是西方为宰制及操控所建构而成的产物。正如弗洛伊德之于精神分析学、皮亚杰之于教育学，萨义德的东方主义无疑强有力地挑战了传统文学史的知识结构与书写模式。现代性、后殖民、第三世界文学等重要议题，为重新思考和书写“台湾文学史”提供了一种契机与参照。“‘殖民现代性’范畴的引入，对于当代台湾文艺理论与批评的确意义深远，它打开了当代文论阐释日据时期台湾文学更开阔的空间，打开了后殖民论述‘在地化’的阐释空间，也为台湾身份认同的复杂性提供了一种更为细腻的解释”[14]113。“后殖民”已成为台湾文学批评与文学史书写的重要部分。

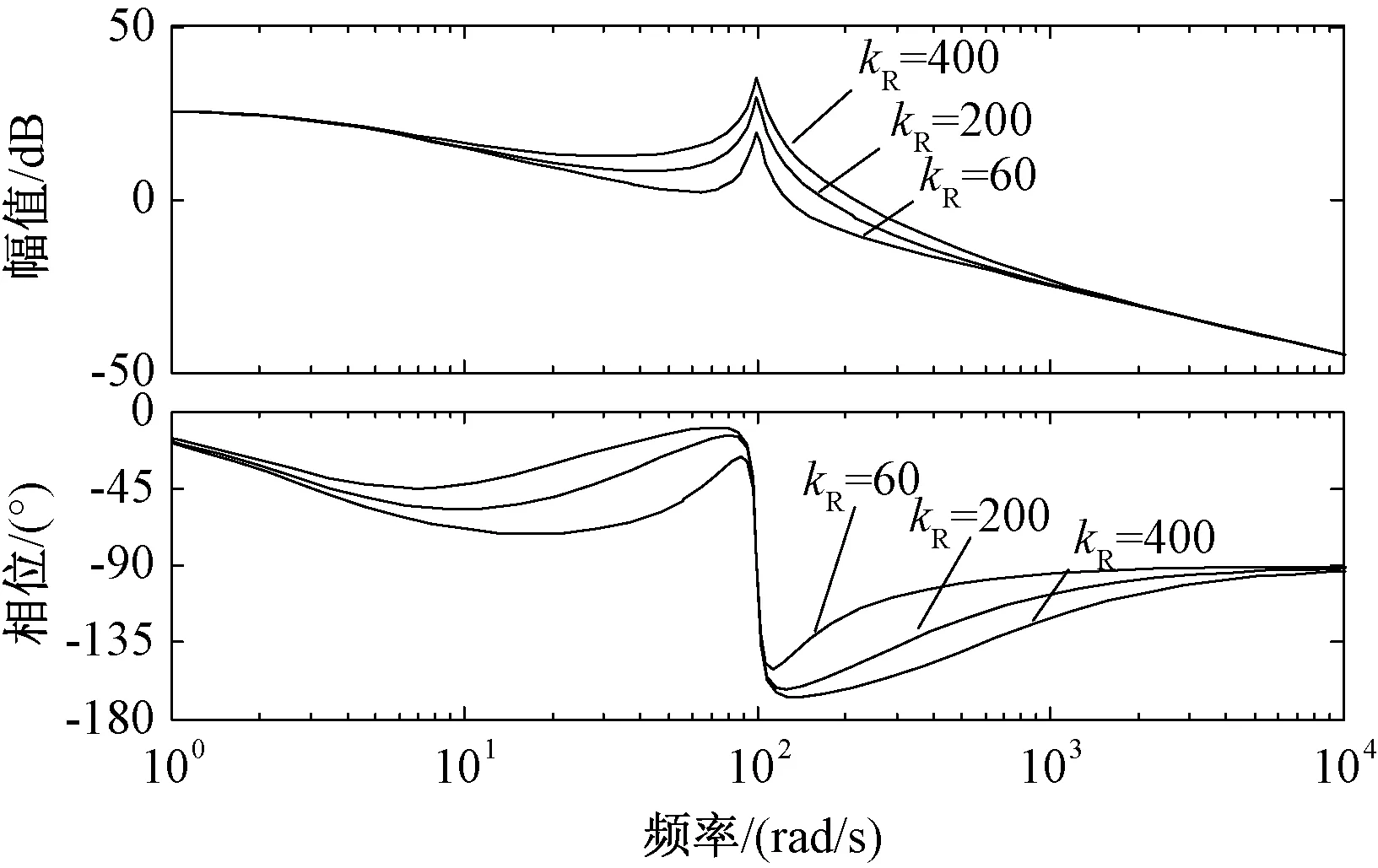
图4 开环传递函数的伯德图Fig.4 Bode diagram of open-loop transfer function

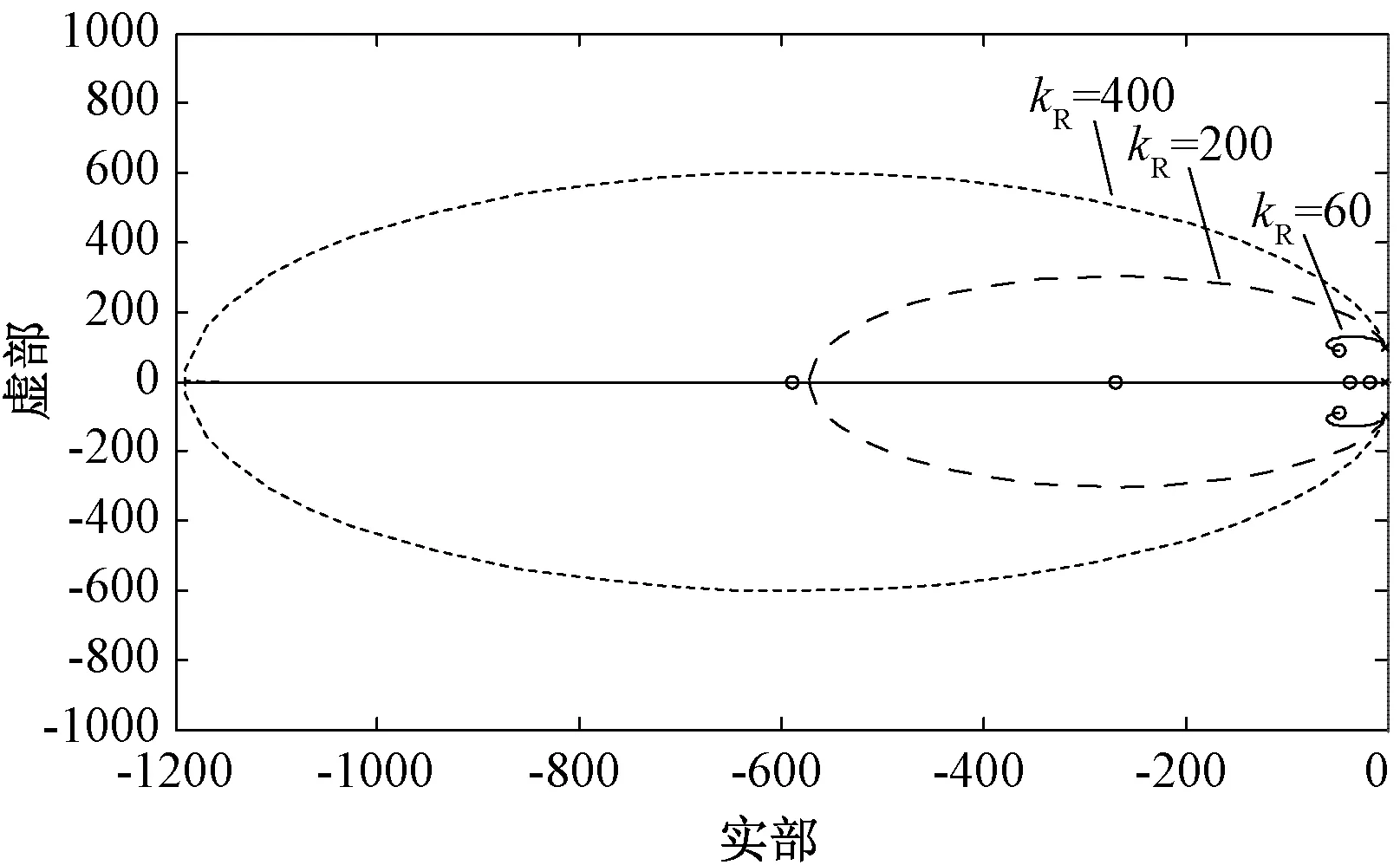
图5 系统根轨迹图Fig.5 System root-locus diagram

由图4、图5容易看出，kR越大系统对二倍频环流的抑制作用也就越强，但随着kR的逐渐增大系统的闭环极点越接近虚轴，系统的稳定裕度也会随之变小，所以kR也不能过大。当MMC重载时桥臂电流中的谐波含量较低，因此选取较小的kR即可；当系统轻载时桥臂电流中的谐波含量较高，为使环流畸变率不超过规定范围，应选取较大的kR。因此不同功率的负载大小对应不同的kR。在单位功率因数运行的MMC中，等效直流侧电流idc代表输入功率的大小，因此设定参数调整规则为：

(13)

式中，kR0为准PR控制器谐振基准系数，其值为系统满足控制要求的最小kR与idc的比值，需要根据不同的情况选择不同的kR0。值得注意的是，在实际应用中需要对kR进行限幅，一方面因为当idc很小时变换器已经接近空载，此时已无必要进行环流抑制，另一方面，此时根据式(13)计算出的kR过大，系统可能不稳定。

4.2 环流控制器的前馈补偿

对于MMC而言，桥臂环流中除二倍频环流外还有受子模块电容电压影响所产生的其他偶数次环流。为了从源头上抑制其他偶数次环流，本文按扰动补偿的复合控制方法对子模块电容电压的干扰进行前馈补偿，如图6所示。

图6 带前馈补偿的环流控制器Fig.6 Circulation controller with feedforward compensation

根据图6得出vhk扰动作用下的输出为：

(14)

式中，Go(s)=1/(Ls+1);GPR(s)为准PR控制器。

若要消除扰动对输出的影响，则Cn(s)=0，可得：

(15)

则式(15)为桥臂子模块电容电压扰动vhk的全补偿条件。虽然Gn(s)在工程上能够实现，但是控制过程较为复杂，因此可以对扰动信号进行稳态全补偿，此时取

(16)

5 仿真结果

为了验证带前馈补偿的准PR控制策略的可行性，在Matlab/Simulink平台上搭建三相MMC仿真模型，进行仿真验证。准PR控制器谐振基准系数kR0=200，谐振系数限幅值kRmax=1000，比例系数kp=4，截止频率ωc=3Hz，谐振频率ω0=100Hz。每个桥臂的子模块数为4，其他仿真参数如表1所示，调试方式为载波移相脉宽调制(Carrier Phase Shifted PWM，CPS-PWM)。

图7为没有加环流控制器之前A相的波形。从图7(a)可以看出，环流中的高次谐波导致桥臂电流发生畸变，为非标准的正弦波。从图7(b)可以看出，环流由直流分量和交流分量组成。图7(c)通过对环流进行FFT分析，验证了环流中除直流分量外还含有偶数次谐波分量，尤其是二倍频幅值波动比较大。

表1 仿真参数Tab.1 Simulation parameters

图7 环流抑制前波形Fig.7 Waveforms before circulation inhibition

图8为加入不带前馈补偿的自适应准PR控制器之后A相波形。从图8(a)中可以看出，桥臂电流波形得到一定程度的改善。结合图8(b)和图8(c)可以看出，桥臂环流中的二倍频分量得到很好的抑制，但是单个的准PR控制器不能对其他偶数次环流进行抑制，其他偶数次环流依然存在。

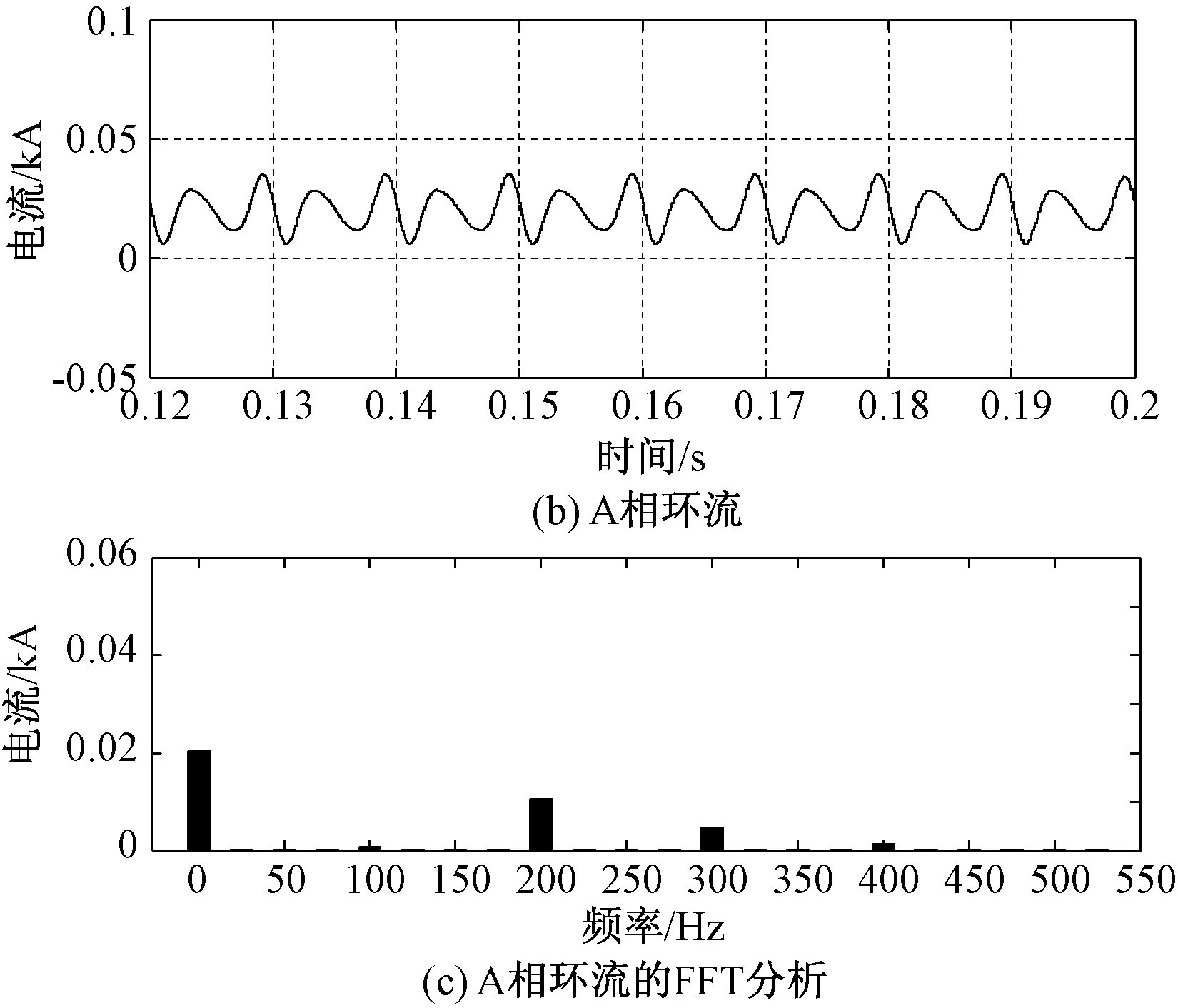
图8 自适应准PR控制的波形Fig.8 Waveforms of adaptive quasi-PR control

图9为在图8的基础上加入前馈补偿之后A相波形。从图9(a)可以看出，相对于图8(a)，桥臂电流波形得到更好的改善，基本上趋于正弦。从图9(b)和图9(c)图可以看出，其他偶数次环流也得到很好的抑制，环流的波动成分很小，基本只含直流分量。由此可以证明所提出的带前馈补偿的自适应准PR控制器只需要一个控制器可以同时抑制MMC桥臂电流中的各偶数次谐波。

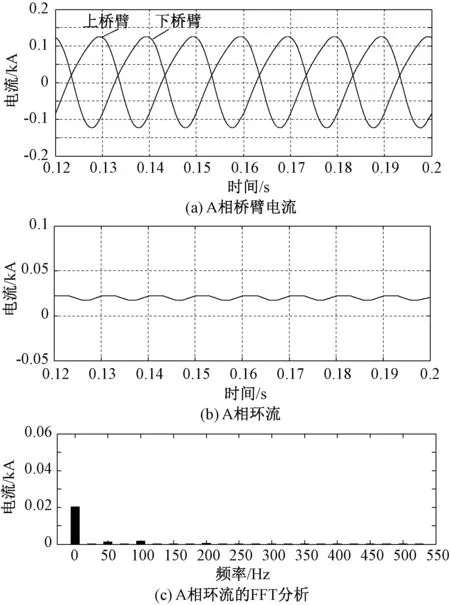
图9 带前馈补偿的自适应准PR控制的波形Fig.9 Waveforms of adaptive quasi-PR control with feedforward compensation

为了进一步验证所提出控制策略的动态稳定性，对交流侧的输出功率的改变进行仿真验证，结果如图10所示。从图10(a)可以看出，MMC稳定运行后，在负载突然增大和突然减小时，A相桥臂电流波形经过短暂的波动后很快处于稳定状态，且电流波动不大。从图10(b)可以看出，在负载发生突变时经过短暂的震荡后，偶数次环流依然得到很好抑制。由此可见，在动态条件下，所提出的的控制策略仍然有很好的抑制效果。

图10 MMC功率发生突变时的仿真波形Fig.10 Simulation waveforms of MMC when power changes

6 实验验证

考虑到实验室电压等级与容量的限制，搭建的实验样机的参数如表2所示，控制器参数和仿真参数相同。主电路控制核心为数字信号处理器TMS320F2812，选用型号为EP2C8Q208C6的FPGA作为TMS320F2812与各模块之间的接口。

表2 实验参数Tab.2 Experimental parameters

图11为未加环流控制器前A相桥臂电流和环流的实验波形，可以明显看出桥臂电流由于含有偶数次环流发生严重的畸变。图12为加入环流控制器后的A相桥臂电流和环流的实验波形，可以看出桥臂电流得到明显的改善，环流得到了很好的抑制。

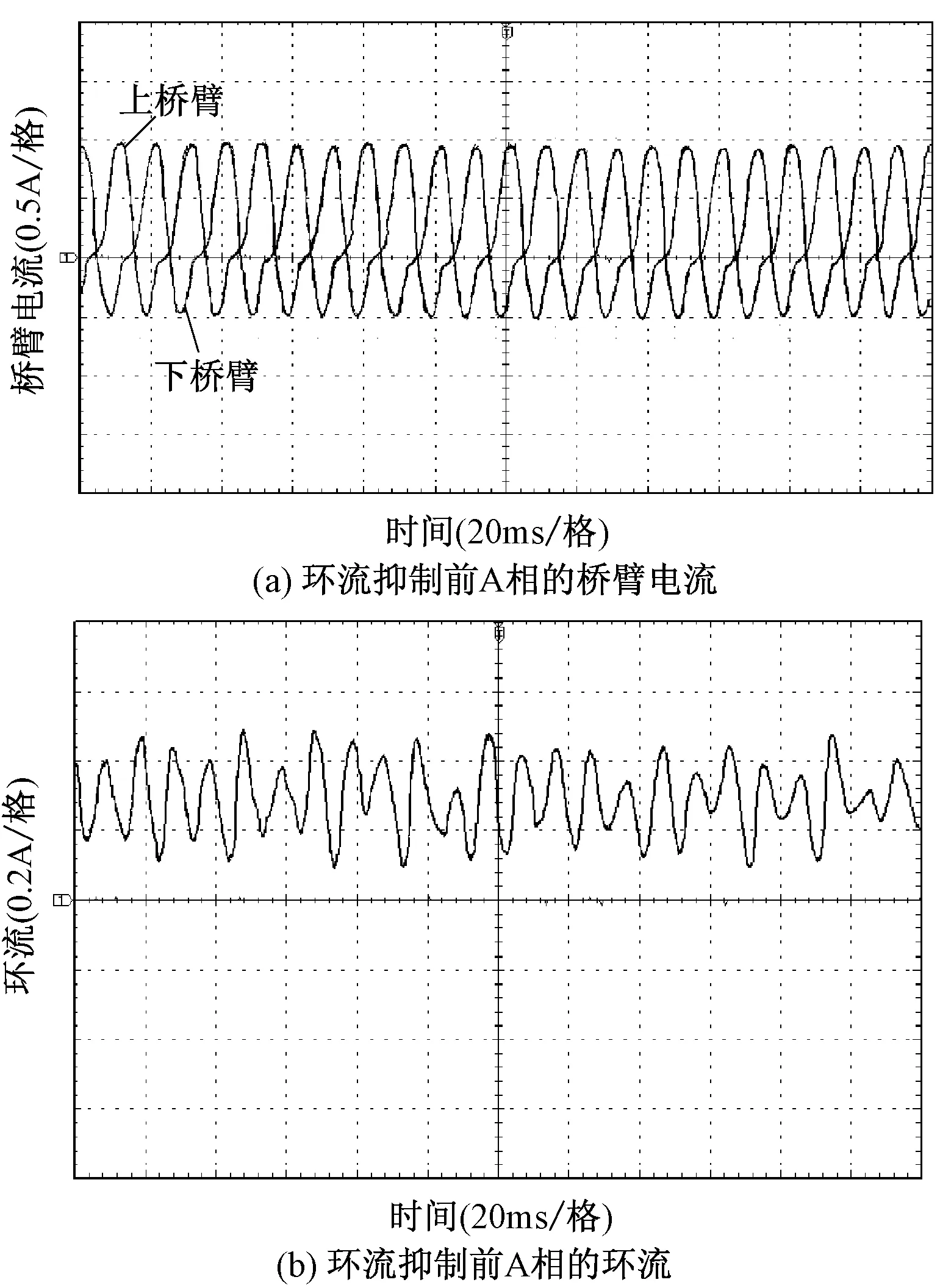
图11 环流抑制前实验波形Fig.11 Experimental waveforms before circulation inhibition

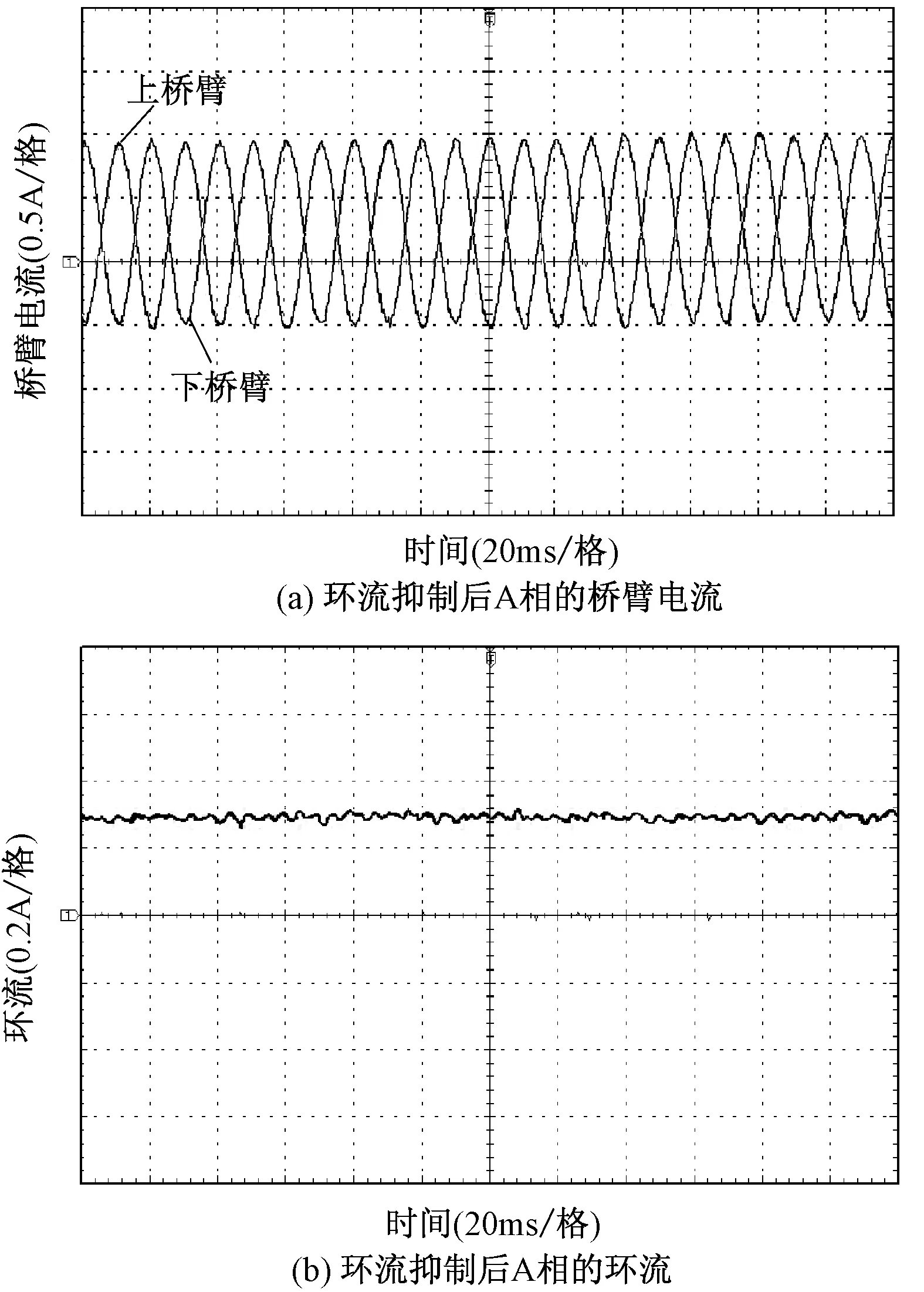
图12 环流抑制后实验波形Fig.12 Experimental waveforms after circulation inhibition

图13为动态条件下A相环流的实验波形，可以看出当负载发生突变时环流经过短暂的调整后又能重新回到稳态。实验结果进一步验证了所提的控制策略的可行性。

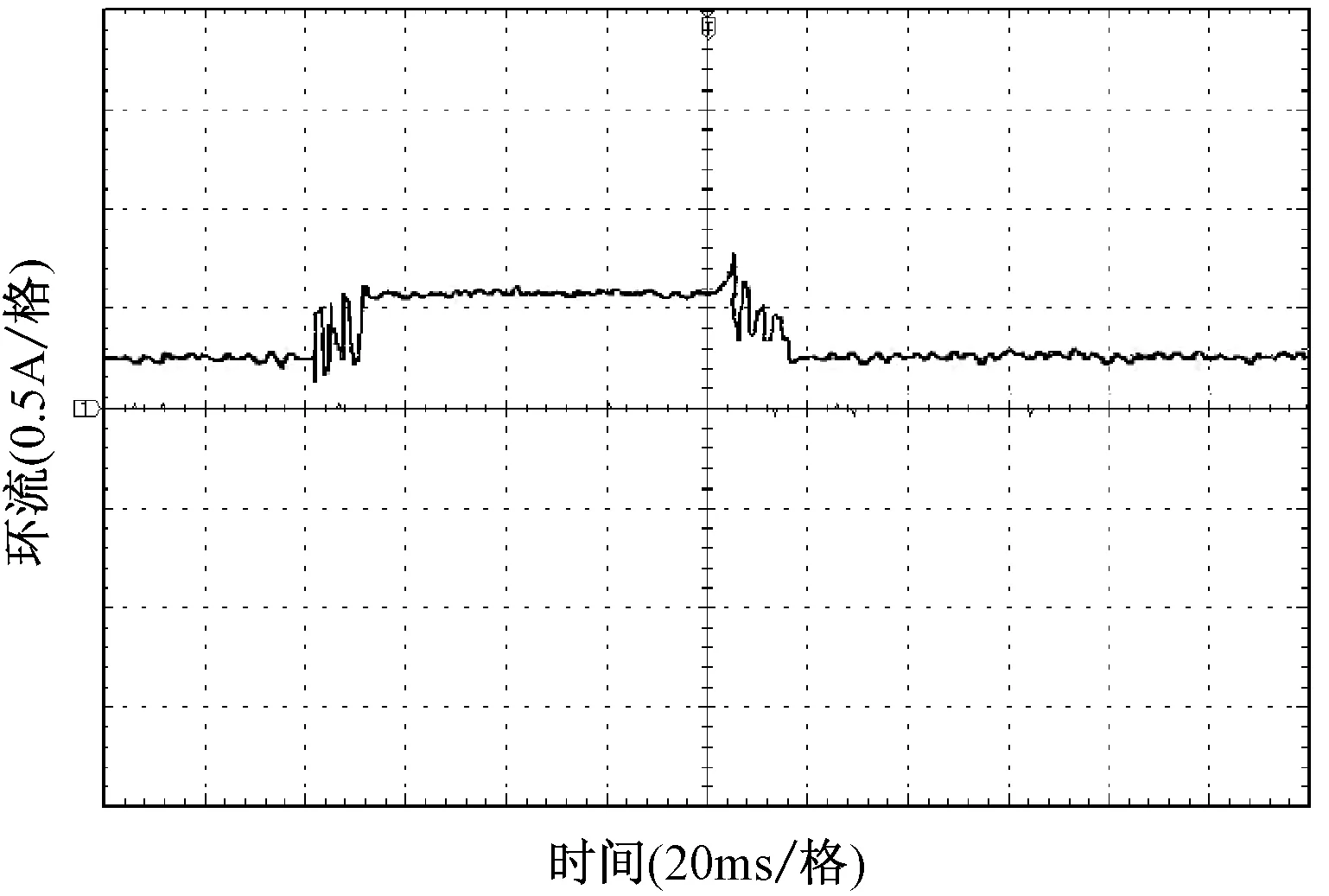
图13 负载发生突变时环流的实验波形Fig.13 Experimental waveform of circulation with abrupt load

7 结论

根据MMC的拓扑结构，详细分析了其内部环流特性，证明了桥臂中二倍频环流的存在，并说明了子模块电容电压波动会影响环流产生其他偶数次波动。为了抑制MMC桥臂环流中的二倍频环流，提出了一种自适应准PR控制的方法，并且给出了相关参数的调整规则；同时选择合适的前馈补偿控制器以抑制子模块电容电压的波动所产生的其他偶数次环流。仿真和实验的结果验证了此方案能够有效地抑制桥臂环流的交流部分。该方法只需要一个谐振控制器就能同时抑制全部的偶数次环流，且能适应不同大小的负载，结构简单，在工程中易于实现，有很高的实用价值。