交错并联双向LLC谐振变换器的通道控制分析及最佳换相点的研究

杨玉岗， 薛文彦， 黄伟义， 许 静

(1. 辽宁工程技术大学电气与控制工程学院， 辽宁 葫芦岛 125105; 2. 国网安徽省天长市供电公司, 安徽 天长 239000)

1 引言

LLC谐振变换器被广泛应用于光伏发电系统、LED驱动电源和变频微波炉电源和电动汽车充电桩等领域[1,2]。随着电源输出频率的不断上升，为了减小变换器中的电流纹波和体积、增大功率密度，在LLC变换器中引入交错并联技术。为了进一步提高变换器的效率、拓展高效运行区间，文献[1]对N相交错并联Buck变换器在全负载情况下的导通通道数进行最优化调整，从而得到使损耗达到最小化的条件[3]。为了实现变换器双向传输效率，且无论正向还是反向工作时，都具备LLC变换器的软开关特性，不需要额外的缓冲电路，文献[2]提出一种双向全桥CLLLC谐振直流变化器。但该拓扑结构不能实现变换器在全负载范围内的高效率传输。

本文在交错并联双向LLC谐振变换器中引入通道控制技术，对变换器中的各部分损耗进行详细分析，为了直观看出不同工作区域下各部分损耗的主次关系，绘制各部分功率损耗曲面图。运用数值计算法和仿真法对换相点电流进行优化分析。最后利用实验验证通道控制技术在交错并联双向LLC谐振变换器中可实现全负载范围内的高效率传输。

2 双向LLC谐振变换器的损耗分析

交错并联双向LLC谐振变换器的拓扑结构如图1所示，为了使变换器在正向和反向工作时的特性一致，将变换器设计为2个谐振网络的参数相对称的结构，另外变换器的漏感还可以充当一部分的谐振电感，有利于磁件的集成[4]。2路共同为一个负载供电，原边侧的逆变电路和谐振网络以及副边侧的整流电路均保持独立运行的状态。

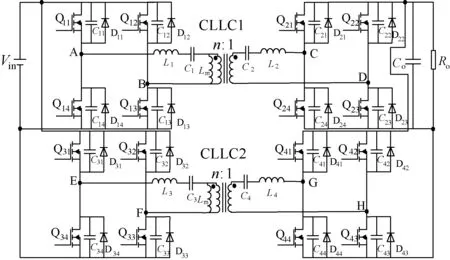
图1 交错并联双向LLC谐振变换器的拓扑结构Fig.1 Circuit to pology of interleaved parallel bi-directional LLC resonant converters

首先分析双向LLC谐振变换器中的各部分损耗。直流谐振变换器在工作中所产生的损耗[5,6]，可以分为5大类：逆变侧开关网络的损耗、变压器原副边谐振网络的损耗、变压器副边整流二极管的损耗、输出滤波电容的损耗以及变压器的损耗[7,8]。

2.1 整流二极管的损耗分析

整流二极管上流过的电流波形近似于正弦波，首先分析各时间段流过整流二极管的电流，设流过整流管D21，D22的电流分别为：

(1)

(2)

式中，ωr为谐振角频率；Tr为整流二极管导通时间；Ts为工作周期。

已知流过整流管的电流在一个谐振周期内的平均值ID.ave为：

(3)

式中，Io为变换器的输出电流。

可以求得流过整流二极管的电流有效值I为：

(4)

式中，fo为工作频率与谐振频率的比值，称为归一化频率。

则相应的整流二极管上的损耗PD为：

(5)

式中，VD为二极管的正向导通压降；iD为整流二极管上流过的电流。

2.2 开关管的损耗分析

开关管的损耗包括：导通损耗、驱动损耗和关断损耗。

(1)导通损耗

导通损耗即开关管导通过程中在开关管的通态电阻上产生的损耗，由于死区时间一般相对于开关周期来说可忽略不计，因此在忽略死区时间的条件下，变换器逆变侧开关管的导通损耗PM.on为：

(6)

式中，rds.on为开关管的通态电阻；IQ.rms为开关管的谐振电流；Ir.rms为变压器原边侧谐振电流有效值。

(2)驱动损耗

驱动损耗是由开关管的栅源极间的电压对寄生电容充放电而产生的，可得损耗为：

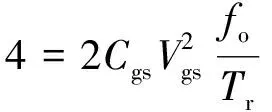
(7)

式中，Vgs为开关管栅源极间的驱动电压的幅值；fs为工作频率；Cgs为开关管栅源极间的寄生电容。

(3)关断损耗

已知变换器逆变侧的开关管可实现ZVS，忽略开关管的开通损耗，对开关管的关断损耗进行计算。

开关管在实际工作中无法瞬间完成关断，当开关管Q11、Q13关断时，在关断过程中流过开关管Q11的电流为：

(8)

式中，ILp为励磁电流的峰值；tf为开关管的关断时间。

由于开关管的下降时间很短，讨论此时间段内的谐振电流大小时，可忽略不计，故该时间段内认为谐振电流ir与励磁电流峰值ILp相等且不变，因此有下列等式：

(9)

式中，iQ11为开关管Q11的电流；iC11为结电容C11的电流；iC14为结电容C14的电流；VC14为结电容C14的电压；VC11为结电容C11的电压；Vin为输入电压。

变换器逆变侧的开关管均为同一型号，且应有同一桥臂上下开关管的寄生电容的充放电过程同时结束，则有：

(10)

联立式(8)～式(10)可得：

(11)

可以求出开关管Q11两端的电压VQ11为：

(12)

可进一步求出开关管Q11的关断损耗PQ11.off为：

(13)

由于一个周期内4个开关管的关断情况相同，因此总的开关管的关断损耗Poff为：

(14)

式中，n为变压器的变比；Vo为输出电压；Lm为励磁电感。

2.3 磁件的损耗分析

该变换器的电路拓扑中包括3个磁件：2个谐振电感和1个变压器，对其各自的损耗进行分别计算。

2.3.1 变压器中的损耗分析

变压器中的损耗分为铜损和铁损。

(1)铜损的计算

铜损也称为绕组损耗，包括直流损耗与交流损耗。变压器工作于高频状态时，直流损耗较小可忽略，只需计算交流电阻的损耗。

直流电阻Rdc为：

Rdc=LNRΩ/m[1+α20(Tmax-20)]

(15)

式中，L为平均每匝长度；α20为20℃时的电阻率常数，数值为0.00393;RΩ/m为所选取导线的20℃时单位米直流电阻；Tmax为最大允许工作温度。

可以得到交流电阻Rac为：

(16)

式中，p为绕组层数；h为有效层厚度；δ为集肤深度。

已知流过变压器原边交流电阻的电流为谐振电流，变压器原边侧谐振电流的有效值Ir.rms为：

(17)

式中，Po为变换器的输出功率。

结合式(1)和式(4)可得到变压器副边侧谐振电流有效值Is.rms为：

(18)

(19)

式中，ID.rms为整流二极管谐振电流。

因此可以得到变压器副边的铜损Psec为：

(20)

式中，rsec为变压器副边电阻。

可计算出变压器总的铜损PT.cu为：

PT.cu=Ppri+Psec

(21)

式中，Ppri为变压器原边的铜损。

(2)铁损的计算

由相应的斯坦梅茨公式可得变压器的铁损为：

(22)

式中，Bmax为变压器的磁感应强度的峰值；kc=16.9、α=1.25、β=2.35均为常量；Vc.T为所用变压器的磁件体积。

2.3.2 谐振电感中的损耗分析

变压器原副边谐振电感的总损耗分为铜损和铁损。

铜损PCu.Lr为：

(23)

铁损PFe.Lr为：

(24)

式中，rL1、rL2、Vc.L1、Vc.L2分别为变压器原副边侧谐振电感的交流电阻和所用磁件体积，两谐振电感所用磁件相同，对应的参数kc=16.9、α=1.25、β=2.35也相同，且均为常量。

2.4 谐振网络中导通损耗的分析

谐振网络中包含变压器原副边侧的谐振电感与谐振电容，两谐振电感对应的交流电阻所产生的导通损耗即为谐振电感中的铜损[9]。因此该损耗为变压器原副边侧的谐振电容上的等效电阻所产生的导通损耗Pnet.on为：

(25)

式中，rC1、rC2分别为变压器原副边谐振电容的等效电阻。

2.5 输出滤波电容上的损耗

流过滤波电容Co的电流iCo为：

(26)

则流过输出滤波电容的电流有效值ICo.rms为：

(27)

因此该滤波电容上产生的损耗PCo为：

(28)

式中，rCo为滤波电容的串联寄生电阻。

当工作频率不在谐振频率点时，引入交错并联技术其输出滤波电容上的损耗PCo.N所占比重很小且公式繁琐，故作近似处理，即为：

(29)

式中，fN为引入交错并联技术后的归一化频率。

以上对双向LLC谐振变换器中各部分的损耗均做了详细的分析，为了减小变换器中的损耗并在全负载范围内实现较高的传输效率。从而引入交错并联技术和通道控制技术[10,11]。

3 通道控制下交错并联双向LLC谐振变换器最佳换相点的选取

3.1 通道控制原理概述

通过改变多通道变换器的导通通道数，有效地控制其导通损耗和开关损耗，为通道控制技术。当变换器运行在满载时，增加变换器的导通通道数，减小导通损耗；轻载时，为了减小变换器多余的开关损耗可采用减小变换器的导通通道数，因此，通过对变换器导通通道数的控制，使其变换器的转换效率得到很大的提高，同时拓宽了变换器的高效运行空间[1]。

在工作过程中工作通道数发生改变，则各部分对应的损耗也将会发生相应的变化。当输出功率一定时，随着工作通道数的增加，每相流过的电流相应减小，开关损耗及导通损耗降低，由于磁件个数增加，磁损耗增加；随着工作通道数的减小，每相流过的电流相应增加，开关损耗及导通损耗会增加，由于磁件个数减小，会减小磁件损耗。因此需要在不同的负载条件下选取较为合理的工作通道数，以求在全负载范围内均能实现高效率[3]。

3.2 基于通道控制下最佳换相点的选取

根据第2节对变换器损耗的分析，可以得到当工作通道数为N时的总损耗为：

(30)

式中,Ptotal.N为除磁件以外的变换器中所有的导通损耗；PCo为输出滤波电容上的损耗；Poff为开关管的关断损耗；Pdrive为开关管的驱动损耗；Ps为驱动损耗、关断损耗和输出滤波电容的损耗的总和；Pon为N通道上总的导通损耗；PFe为N通道上变压器和谐振电感的总铁损。

虽对各部分的损耗进行了详细的分析，但仍不方便推导出最佳工作点(即最小损耗)，为得到最佳的工作点，需要在不同的负载条件下选取最合适的导通通道数，有效缓解变换器的功率损耗、提高变换器的利用率。运用Matlab绘制不同工作区域下各部分损耗的主次关系[1]。各部分功率损耗曲面图如图2所示。

图2 各部分功率损耗曲面图Fig.2 Part of power loss surface diagram

从图2中可以看出，当负载电流较小时，铁损占比较大，而随负载电流的增加，导通损耗占比较大。由图2可知，双向LLC谐振变换器工作在某负载点时会出现工作通道数为N时的损耗等于其在工作通道数为N+1时的损耗，由此求得变换器的换相点电流：

Ptotal.N-Ptotal.N+1=0

(31)

有2种方法可以求解对应的换相点电流：分别为数值计算法和仿真法。

(1)数值计算法

由式(31)可以得到式(32)：

A(fN,fN+1,N,N+1)Io2+B(fN,fN+1,N,N+1)Io+C(fN,fN+1,N,N+1)=0

(32)

式中

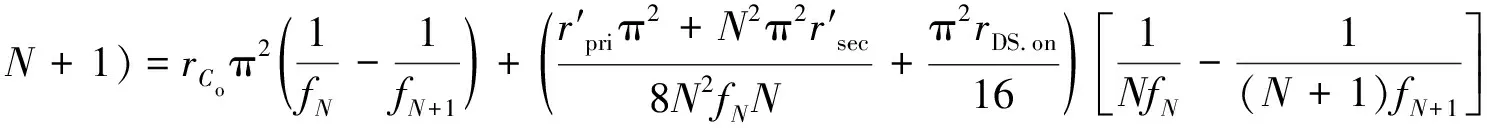
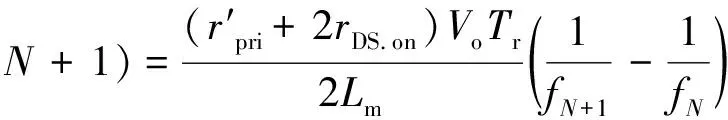
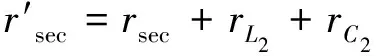
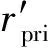
经过一系列复杂的推导，可以得到负载电流和最佳通道数的对应关系：

令A(fN,fN+1,N,N+1)=X

B(fN,fN+1,N,N+1)=Y

C(fN,fN+1,N,N+1)=Z

则

(33)

由上述推导可定量得出各个换相点的电流值，但计算过程繁琐且工作量大容易出错。下面将介绍较为简便且相对直观的仿真法。

(2)仿真法

根据变换器中各部分损耗的分析，选定变换器的参数以后，通过电压增益曲线可基本确定各负载点对应的归一化频率，将得出的归一化频率进行拟合，用与负载电流有关的表达式表示，代入各项损耗中直接对其进行仿真，得到不同工作通道数时变换器的总损耗曲线图如图3所示，从图3中可以直接清晰地看出换相点电流的大小。

图3 不同工作通道数对应的变换器的总损耗曲线图Fig.3 Total loss curve of converter corresponding to number of different working channels

根据仿真法可以直接得出各个换相点的电流值。在正向工作模态下，由单通道切换到2通道工作时的负载电流为10A，由2通道切换到3通道工作时的负载电流为16A。在反向工作模态下，由单通道切换到2通道工作时的负载电流为1.2A，由两通道切换到3通道时的负载电流为2.2A。

4 交错并联双向LLC谐振变换器的实验

下面将用实验验证采用通道控制技术能否实现全负载范围内变换器均有较高的传输效率。实验主要分为2个部分：变换器的正向运行和反向运行。通过实验数据，可得到变换器在不同工作通道数时的效率对比曲线图，继而比较其效率。系统工作参数见表1，实验参数见表2，实验电路系统如图4所示。

表1 系统工作参数Tab.1 System working parameters

表2 实验参数Tab.2 Experimental parameters

图4 实验电路系统Fig.4 Experimental circuit system

根据变换器的实验数据，可以得到效率对比曲线图如图5和图6所示。

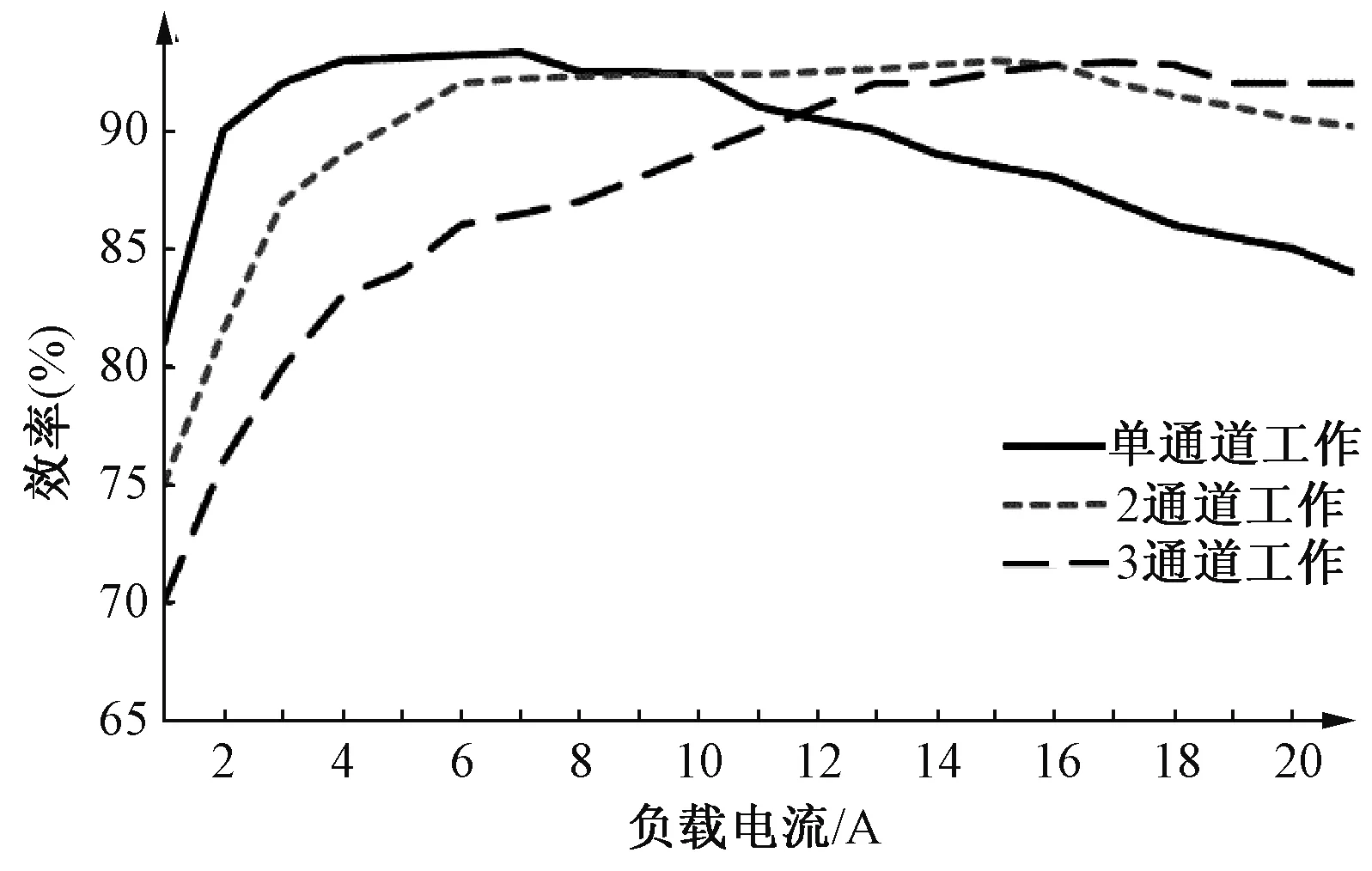
图5 变换器正向工作时的效率对比曲线Fig.5 Efficiency comparison curve when converter operating in forward direction

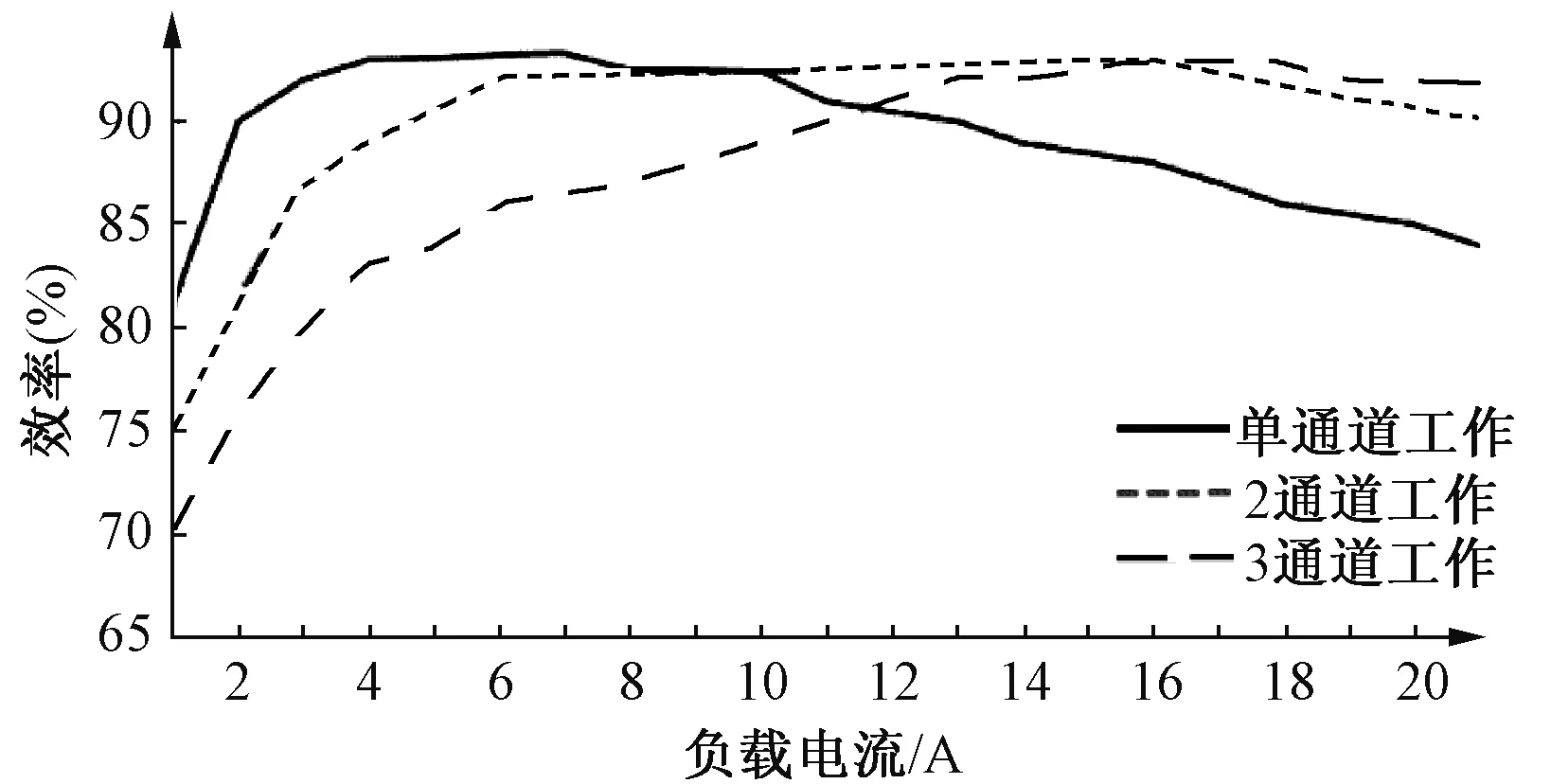
图6 变换器反向工作时的效率对比曲线Fig.6 Efficiency comparison curve for converter in reverse operation

从图6可以明显看出，在半载附近，变换器工作于2通道共同作用的效率比单通道工作时的高，验证了理论的正确性，并且在正向工作和反向工作时，变换器的全负载范围内均有较高的传输效率。

5 结论

对交错并联双向LLC谐振变换器的各部分损耗进行了比较详尽的分析，并且推导出各部分损耗的公式，利用Matlab三维绘图工具绘制了各部分功率损耗曲面图。分别用数值计算法和仿真法求解各个换相点的电流值。最后用实验验证了理论分析的正确性。基于通道控制技术下的交错并联双向LLC谐振变换器在全负载范围内均有较高的传输效率。