一种基于频率响应辨识的开关频率对永磁电机控制环性能影响的新分析方法

俞学初， 蒋 栋

(华中科技大学电气与电子工程学院， 湖北 武汉 430074)

1 引言

近年来，交流永磁同步电机因为其优异的性能，例如结构简单、体积小、重量轻、损耗少、效率高等，在工业领域被大量应用[1,2],具有很好的发展前景。

矢量控制[3,4]和直接转矩控制[5,6]作为交流电机的两种主流的控制方式，最近几十年来得到了长足有效的发展，并且成功地应用在永磁同步电机的控制系统中。在永磁电机的矢量控制系统中，一般采用了电流环作为内环和速度环作为外环的双环控制方式，这既可以保证整个电机系统对指定响应的快速跟随性，又可以保证足够的抗扰性能[7,8]。

在永磁电机控制的内外环性能设计和评估中，一般需要通过分析控制环闭环或者开环波特图的性能指标来评判控制效果，例如系统的截止频率、相位裕度等。基于控制系统平台小信号分析的传递函数辨识方法成为一个极其重要的研究方向。图1展示的是一个电机控制系统中辨识控制环传递函数的典型结构：在参考指令值的基础上注入小信号从而激励系统的小信号响应，将小信号的激励与响应同时送入辨识模块，从而得到传递函数的波特图。

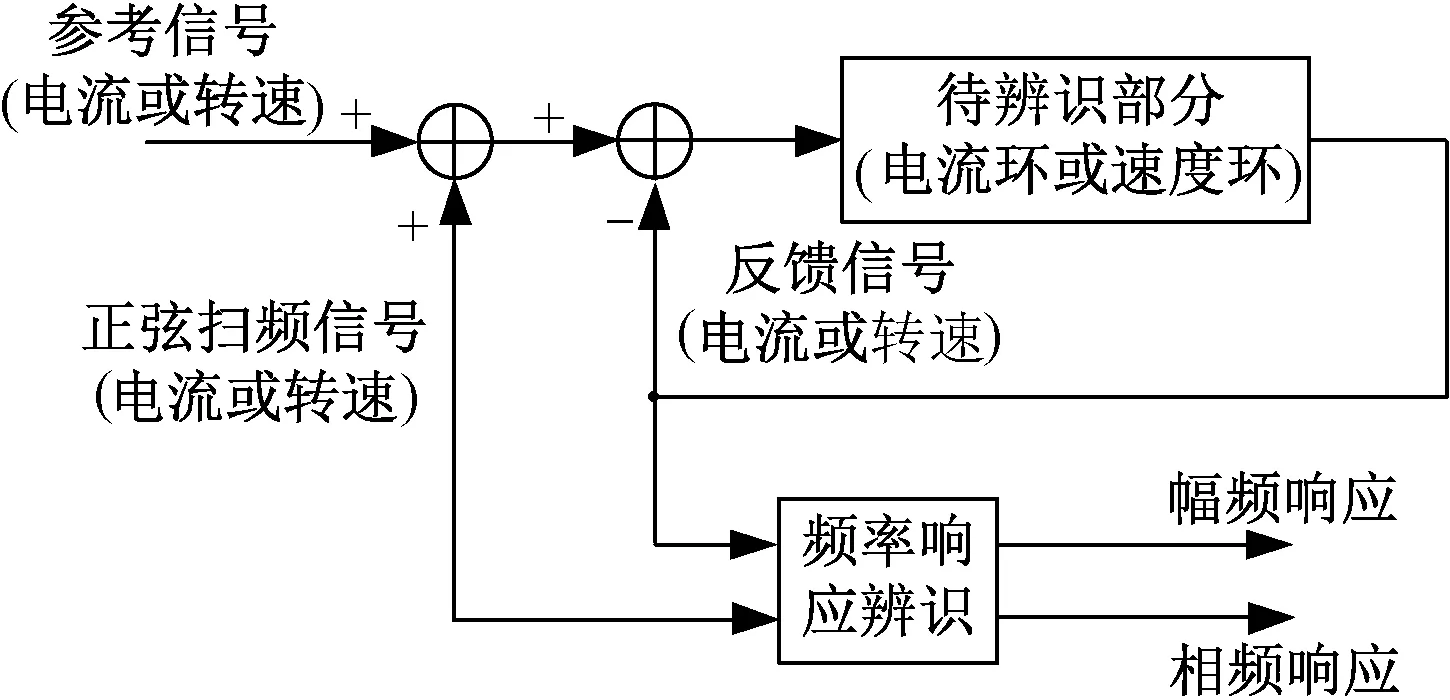
图1 通过小信号分析方法辨识传递函数Fig.1 Transfer function identification through small signal analysis

系统的频率响应可以通过不同的方法辨识得到，文献[9]以伪随机二进制信号(Pseudo-Random Binary Sequence, PRBS)作为正激式变换器的激励信号，应用相关分析法辨识得到了系统的频率响应，并分析了PRBS序列的长度对辨识效果的影响。而在文献[10]中，正弦扫频信号用来作为在线辨识机电系统频率响应的激励信号，并且使用了一种自适应最小均方(Least Mean Square, LMS)算法。

闭环控制的性能指标通常和反馈控制的方式有关，比例积分(Proportional-Integral, PI)调节器因为其简单的结构，易于数字实现，常被应用于工程控制中。文献[11]分析了dq旋转坐标系下三相电压型逆变器(Voltage Source Inverter, VSI)带阻感负载的电流环模型，指出电流环的截止频率与电压、电流反馈信号的采样方式有关，但未与逆变器开关频率联系起来。文献[12]提出了一种能提高控制环截止频率的方式，不过同样没有给出截止频率与开关频率近似的函数关系，同时均没有结合相位裕度这一因素。

电机控制逆变器在脉宽调制(Pulse Width Modulation, PWM)条件下高频开关是实现高性能数字控制的基础。尤其是随着宽禁带电力电子器件的应用，电机控制器的开关频率进一步提高，对电机动态性能的改善也有期望。不过目前国内外针对提高开关频率对电机控制动态性能的改善的研究还较为欠缺，难以充分发挥新型电机控制器的优势。同时传统的频率响应辨识方法常使用M序列作为待辨识系统的辨识输入信号，在计算输入自相关信号与输入输出互相关信号后，使用相关分析法来计算系统的频率响应。在此过程中M序列的产生和相关信号的计算繁琐且对硬件资源负担大。针对这些问题展开了相关研究。

通过理论分析建立了逆变器开关频率对永磁同步电机的电流环和速度环影响的模型，应用不同的设计方式来设置PI调节器的参数。根据电流环具有快速跟随性的特征，参考二阶最佳设计方法，把电流环设计成一个典型I型系统，而速度环一般要求具备良好的抗扰性能，故根据幅频特性峰值最小设计准则，把速度环整定成典型II型系统。模型表明电流环的截止频率与开关频率成正比，而逆变器的开关频率则对速度环的截止频率影响很小，并且两者均具有了足够的相位裕度。同时采用小信号扰动方法，在系统的特定稳态点将整个系统近似等效为一个线性系统，然后利用一系列的正弦信号作为这个系统的输入，其输出必然是相同频率的正弦形式，只是幅值和相位会变化，最后应用一种特定的自适应噪声消除技术，理论分析得出当干扰信号为正弦信号时，整个自适应滤波器可以等效为带通滤波器，对上述输出信号进行自适应滤波，只有特定频率的正弦部分通过滤波器时会被留下来，进而可以依次求得特定频率信号的幅值和相位，于是可以得到一定频率范围内的系统波特图，仿真和实验都验证了这种新方法的正确性和有效性。

2 频率响应辨识原理

自适应噪声消除技术作为一种常见的数字滤波技术，工程上常用于对特定噪声的滤波，如心电图信号中对频率60Hz的电源线干扰的消除，语音信号中噪声的消除等[13]。自适应噪声消除技术的原理如图2所示，其中的主要输入信号包括期望得到的信号s和噪声信号n0，而参考输入信号n1可以是我们指定的一系列信号，如正弦信号、伪随机二进制信号等，其可以与s或n0相关。而自适应滤波器可以采用常见的不同算法实现，如最小均方算法(LMS)[14]、递归最小二乘法(Recursive Least Squares, RLS)[14]等。

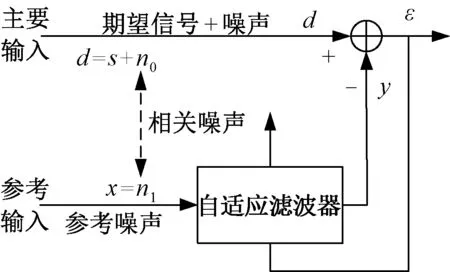
图2 自适应噪声消除技术原理图Fig.2 Principle of adaptive noise canceling system

最小均方算法因为其简单的迭代形式，高效的收敛速度，常用于自适应滤波技术中，其主要离散形式的迭代方程如下:

(1)

式中，xk、yk、dk、εk分别为输入信号、输出信号、期望信号和误差信号的离散形式；wk为每次算法的迭代权重向量；α为算法每次的迭代步长。当迭代步长选择合适时，Widrow证明了最小均方算法对于静态随机过程[15]，期望的迭代权重向量能收敛到最优解w*。

当参考输入信号为正弦信号形式时，即xk用以下形式表达，C,ωr,θ分别为信号的幅度、角频率和初始相位。

xk=Ccos(ωrkT+θ)

(2)

以下将证明，当一定的条件状况满足时，G(z)可以近似等效为一个带通滤波器，如图3所示。

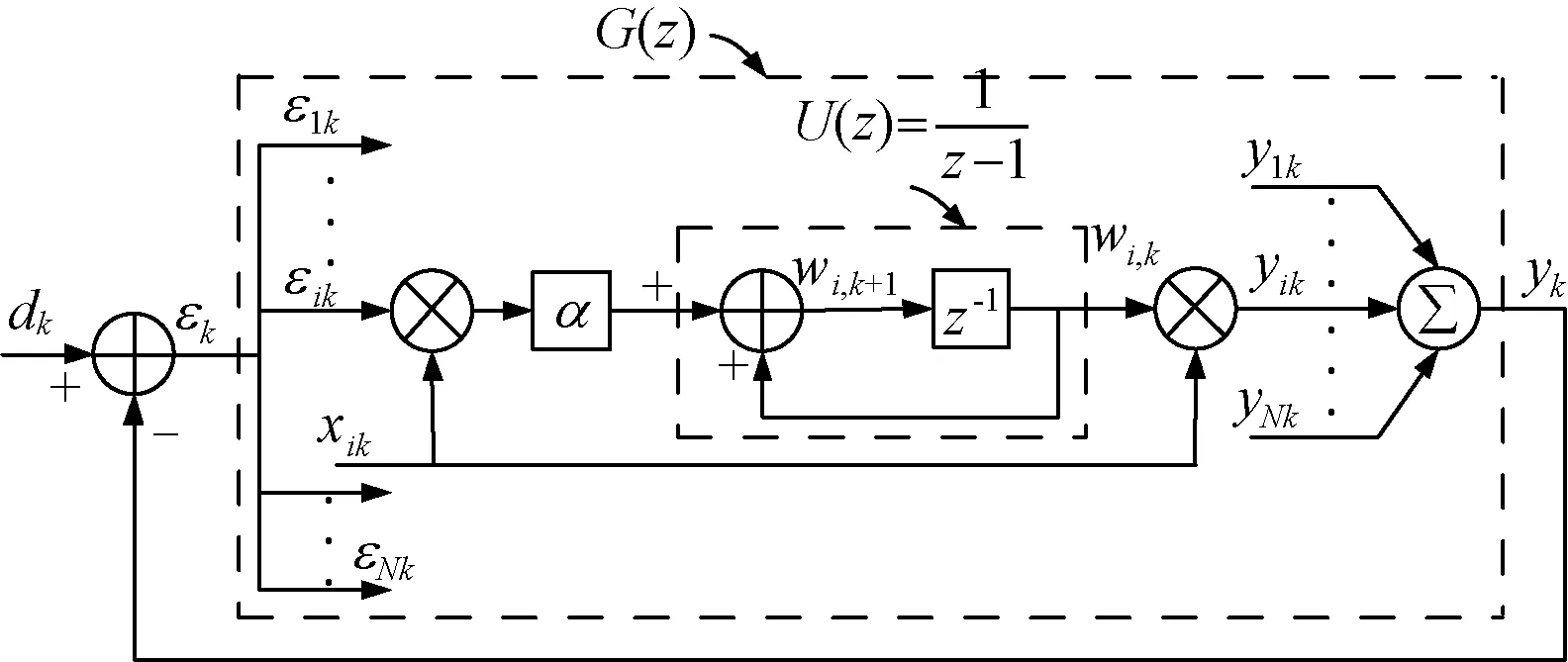
图3 LMS自适应算法的框图Fig.3 Block diagram of LMS adaptive algorithm

作为参考输入信号的任意一个分量，可以写成：

(3)

故图3中信号εkxik的z变换形式为：

(4)

E(z)表示误差信号的z变换形式。如图3所示，LMS算法的权重向量迭代方程可以表示为U(z)=1/(z-1)。将式(4)代入后，以下等式成立。

从而自适应滤波器输出信号的z变换形式表示成如下形式：

(7)

式中，第一个{}表示响应的时不变(TI)成分；第二个{}表示时变(TV)成分。为了得到G(z)的表达式，时变成分可以进行以下处理。将θi展开代入式(7)中的求和项，可以得到：

β(ωrT,N)

(8)

其中β函数定义成如下形式：

(9)

故将式(8)代入式(7)中，可以简化成：

(10)

式中，第一个{}表示式(7)对应的时不变(TI)成分；第二个{}表示式(7)对应的时变(TV)成分。式(6)中的指数成分幅值始终为1，从式(7)～式(10)中可以发现，当TV成分在Y(z)中所占的相对“强度”远远小于TI成分，即β/N≈0时，我们可以忽略TV成分的影响而只保留TI成分。当做了以上适当的处理后，便可以得到从E(z)到Y(z)的线性时不变传递函数G(z)。

(11)

从式(11)中可以看出G(z)在单位圆上有两个极点z=e±jωrT和一个零点z=1/cos(ωrT)，其等效为一个低通滤波器。求得G(z)后，同样图3中从信号dk到信号yk的传递函数H(z)，可以相继得到。

(12)

H(z)的频率响应的波特图如图4所示，从图4中可以看出，此传递函数为一个带通滤波器，当主要输入信号dk有正弦形式的信号时，通过自适应滤波器后，输出信号yk中只有相应频率的成分。

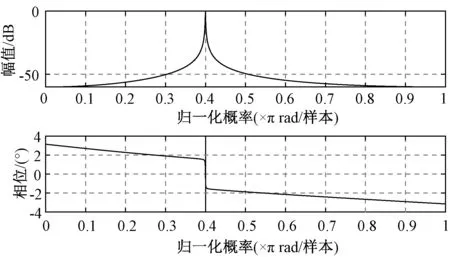
图4 H(z)的频率响应(ω0T=0.4π,α=0.002,C=1,N=2)Fig.4 Frequency response of H(z) (ω0T=0.4π,α=0.002,C=1, N=2)

通过以上的理论分析，证明了当一定的条件满足时，从信号dk到信号yk的传递函数是一个线性时不变模型，效果与带通滤波器相似。当参考输入信号为正弦形式时，主要输入信号经过自适应滤波器时只有对应频率的正弦成分才会被保留下来。

3 电机控制环模型分析

交流永磁同步电机(Permanent Magnet Synchronous Motor, PMSM)应用矢量控制时可以等效为一台他励直流电机，简化了控制策略。

3.1 电流环控制模型

对交流永磁同步电机进行建模后，其dq旋转坐标系下的数学模型如下[16]:

(13)

式中，ud，uq和id，iq分别为电机在dq坐标系下的电压与电流；Ld，Lq分别为电机的交直轴电感(若对于隐极永磁电机，Ld=Lq=L)；R为电机定子端的电阻；ωe为电机的电角速度；ψf为电机的转子永磁磁链。通过分析以上的模型，当电流闭环控制采用PI调节方式时，永磁电机电流环控制框图如图5所示。

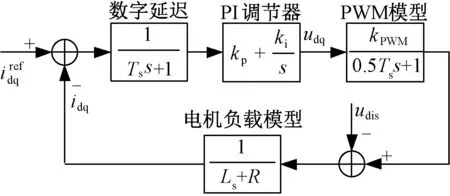
图5 PMSM电流环控制框图Fig.5 Control diagram of current loop for PMSM

图5中Ts为逆变器的开关周期，即中断采样周期，kPWM为PWM调制环节的等效增益。依据以上的控制框图，电流环的传递函数可以写成：

(14)

从式(14)中可以发现，这是一个潜在的三阶系统。而作为内环的电流环而言，应当主要考虑对参考指令的快速跟随性，故工程上常常把电流环的传递函数配置成典型的Ι型系统[17]，即PI调节器的零点与分母中惯性较大的极点相抵消。

(15)

通过式(15)设置后，电流环的传递函数将变成一个典型的二阶系统，为了把系统设计成欠阻尼状态，同时兼顾系统的快速性与稳定性，常把阻尼比ξ设计成0.707，故式(16)成立。

(16)

联立式(15)、式(16)，可以唯一确定PI调节器的比例常数和积分常数。

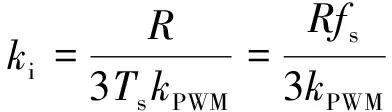
(17)

式中，fs为逆变器的开关频率。可以发现PI调节器的参数与开关频率有关，当传递函数的增益为1时，即|Fo(s)|=1，通过计算后得到，截止频率为：

foc=0.0483fs

(18)

将求得的截止频率代入式(19)计算后可以得到相应的相位裕度(Phase Margin,PM)。

PM=180°-Fo(j2πfoc)≈65.3°

(19)

通过建立永磁同步电机的电流环数学模型以及分析电流环的性能指标，给出了PI调节器参数的设置方式，同时经过理论推导后表明，电流环的截止频率与逆变器的开关周期有关，并且近似为一个正比关系，而相位裕度能达到65.3°。所有的性能指标均保证了电流环快速的跟随性与稳定性。

3.2 速度环控制模型

速度环作为电机矢量控制的外环，影响着电机的调速性能和转矩输出。对于永磁同步电机，其转矩方程如下(忽略摩擦)：

(20)

式中，Te与TL分别为电机的电磁转矩和负载转矩；J为转子的转动惯量；ωm为电机的机械角速度。

对于一般的隐极式永磁同步电机而言，当采用id=0的矢量控制方式时，电磁转矩可通过式(21)求得：

Te=1.5Pψfiq

(21)

式中，P为电机的极对数。

电流环的时间常数远远小于速度环的时间常数，故当速度闭环控制后，电流内环可以近似地等效为一个一阶惯性环节，这也从侧面说明电流闭环控制改造了控制对象，加快了电流的跟随作用。结合式(20)、式(21)两个方程，对于隐极式永磁同步电机，整个速度控制的动态结构框图如图6所示。

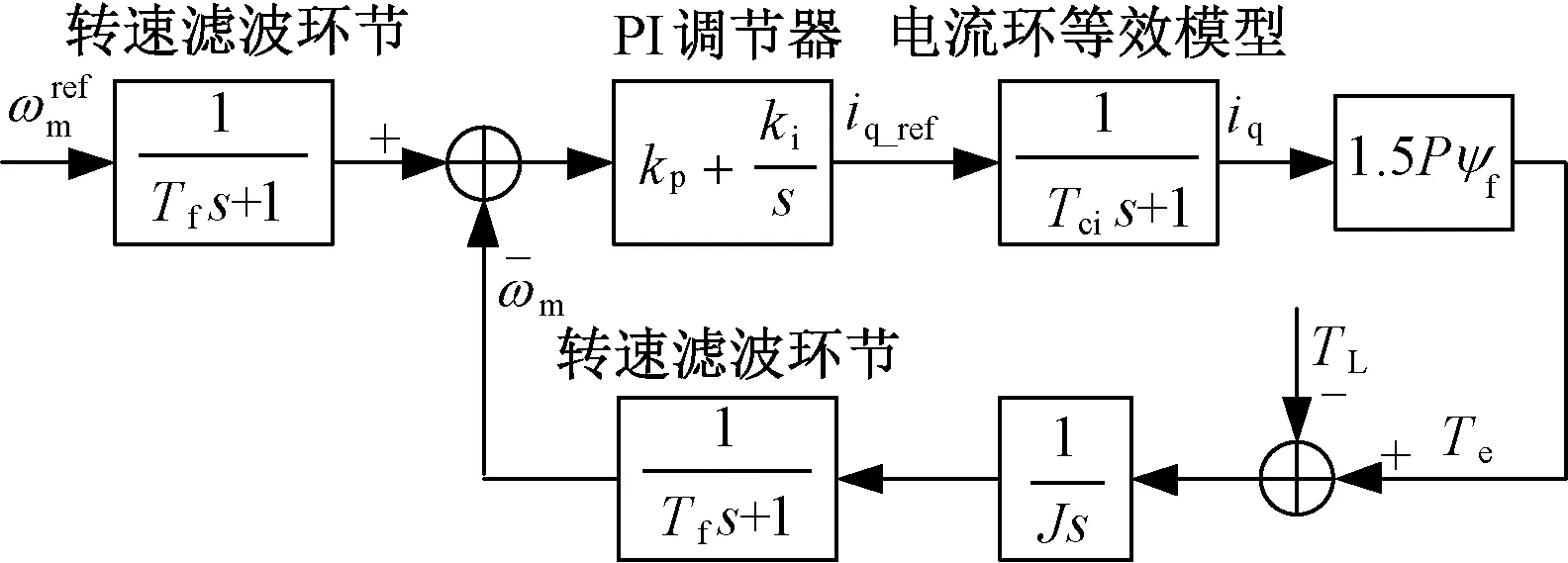
图6 PMSM速度环控制框图Fig.6 Control block diagram of speed loop for PMSM

根据图6所示的控制框图，速度环的传递函数可以写成：

(22)

式中，Ton=Tci+Tf。Ton、Tci和Tf分别为速度环、电流环和速度滤波环节的等效时间常数。

速度环作为控制外环，应当具备良好的抗扰性能，因此速度环首选典型II型系统[17]。典型II型系统一个很重要的参数是中频宽h，工程上一般把中频宽设计成5，经过这样的分析后，速度PI调节器的参数也能随之确定。

(23)

速度环的增益为1时，即|Fos(s)|=1，经过一定的计算可以证明，其截止频率为：

fos=0.0886/Ton

(24)

相位裕度可以达到41.13°。通过2.2小节对电机速度环数学模型的分析，在合理配置速度PI调节器的参数后，结果表明速度环的截止频率与逆变器的开关频率没有直接关系，相位裕度也足够保证系统的稳定性。

4 仿真和实验结果验证

4.1 仿真与实验结果

对一台隐极式永磁同步电机进行仿真验证与实验验证，电机电气参数及其控制系统参数见表1，其完整的矢量控制框图如图7所示。

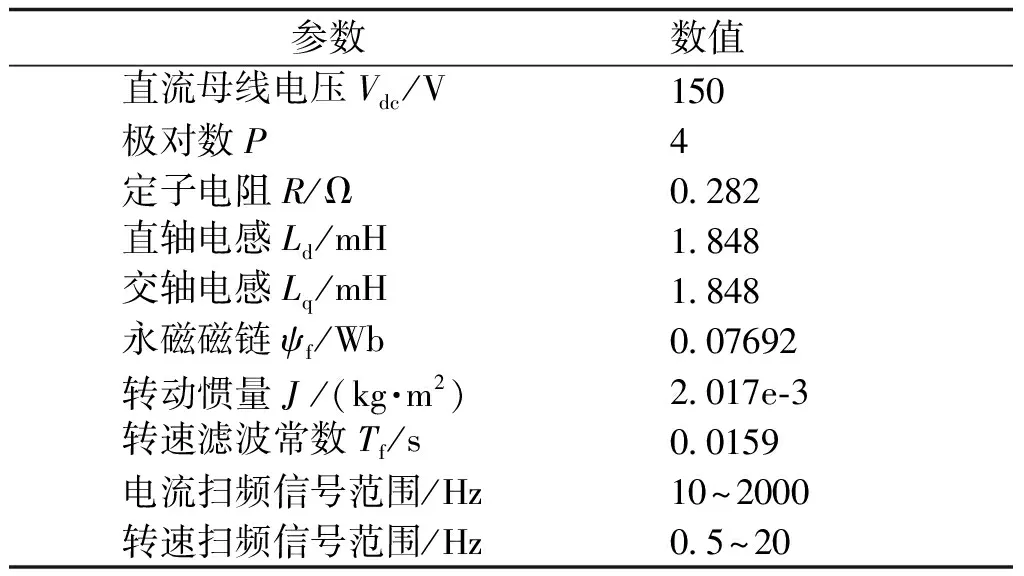
表1 隐极式永磁同步电机参数Tab.1 Parameters of nonsalient-pole permanent magnet synchronous machine

如图7所示，在通常的永磁同步电机矢量框架上，附加的电流扫频信号和速度扫频信号分别用于电流环和速度环波特图的在线辨识，两种扫频信号均是由一定频率范围内的一系列正弦信号组成。为了详细说明在线辨识功能如何实现，主要原理框图如图8所示。

图7 永磁同步电机矢量控制框图Fig.7 Vector control block diagram of PMSM

图8 电流环与速度环在线辨识原理图Fig.8 Online identification schematic of current loop and speed loop

一定频率范围内的正弦扫频信号添加在参考信号端，当其通过待辨识系统后，因为待辨识系统可以近似地等效为一个线性时不变系统，因此扫频信号产生的响应信号为相同频率的正弦信号，只是幅度与相位不同。然后将扫频输入信号与其响应信号用于自适应滤波算法求解，由于自适应滤波器可以近似等效为一个带通滤波器，故可以求得响应信号中特定频率的幅度和相位，与扫频输入信号比较，进而可以计算得到频率响应。

在MATLAB/SIMULINK中搭建图7所示的永磁同步电机矢量控制仿真模型，并使用自适应噪声消除原理，通过LMS算法能够在线辨识得到不同开关频率下的电流环与速度环的频率响应，用于与理论结果对比分析。仿真结果如图9和图10所示。

图9 不同开关频率的电流环波特图(仿真结果)Fig.9 Current loop bode diagram with different switching frequency (simulation result)

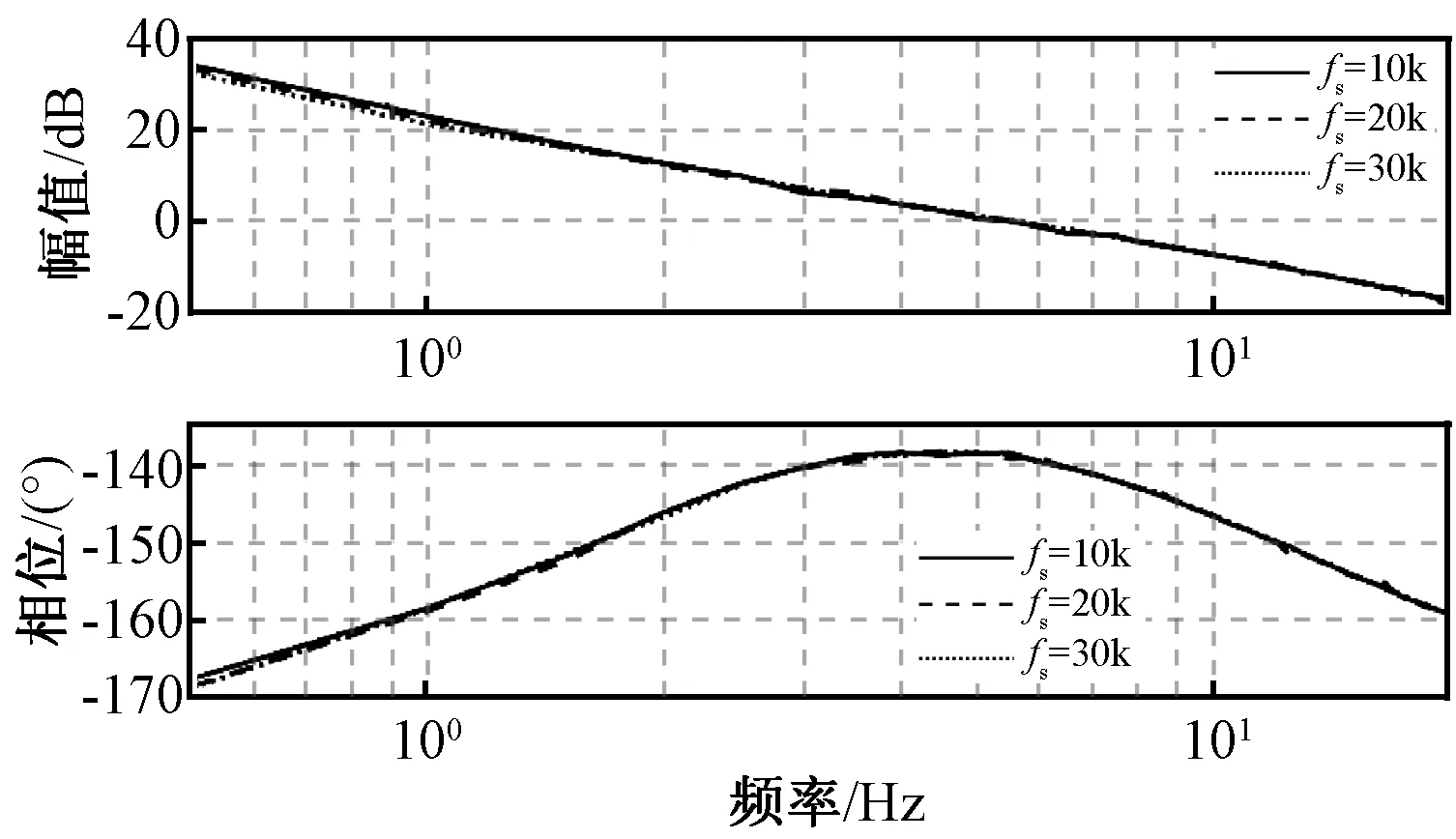
图10 不同开关频率的速度环波特图(仿真结果)Fig.10 Speed loop bode diagram with different switching frequency (simulation result)

为了验证所提出的新方法的准确性和有效性，采用了美国TI公司提供的TMS320F28335数字控制芯片对一台隐极式永磁同步电机进行id=0的矢量控制实验，并使用频率响应分析仪来测量不同开关频率下的电流环与速度环波特图，实验装置如图11所示。

图11 实验装置Fig.11 Experimental setup

在电机转速为600r/min的稳态情况下使用频率响应分析仪测量得到的不同开关频率下的电流环与速度环波特图如图12和图13所示。

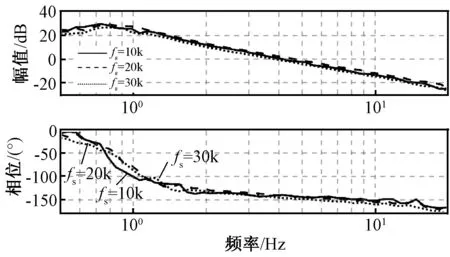
图13 不同开关频率的速度环波特图(实验结果)Fig.13 Speed loop bode diagram with different switching frequency (experimental result)

4.2 结果分析与讨论

根据仿真与实验所得到的数据以及波特图，相应地就可以求得内外控制环的截止频率以及相位裕度，完整的结果见表2和表3。

表2 不同开关频率电流环性能指标Tab.2 Performance indicators of current loop under different switching frequency

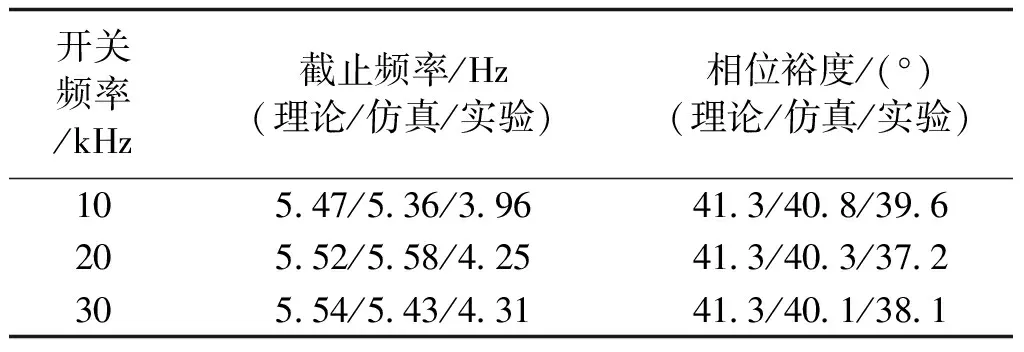
表3 不同开关频率速度环性能指标Tab.3 Performance indicators of speed loop under different switching frequency

从表2和表3中可以发现，无论是对于电流控制环还是速度控制环，仿真所得到的数据结果均与理论分析结果相差无几，一方面是因为仿真环境没有额外因素的干扰，另一方面也验证了所提出的新辨识方法的正确性与有效性。但观察实验结果可以发现，电流控制环与速度控制环的截止频率均比理论分析结果小一些，相位裕度也是如此，这主要是由于实验中其他因素的干扰，比如信号采样滤波环节带来的延迟，算法执行环节带来的延迟等。同时由于真实电机系统的复杂性以及非线性，测量控制环波特图时，必须合理地考虑扫频小信号幅值与参考指令值的比例，比例过小可能会导致扫频小信号在反馈信号中没有体现，比例过大可能会导致电机的异常运行。

5 结论

基于一种自适应噪声消除技术的应用，提出了一种基于正弦形式小信号注入的频率响应辨识的新算法，并且在理论上证明了算法的正确性。同时针对永磁电机的矢量控制方法，合理地建立了电机内外控制环的数学模型,通过控制器最优整定方法设置控制参数后，指出了电流控制环的截止频率近似地与逆变器的开关频率成正比，而速度控制环的截止频率则与转速测量滤波环节的时间常数有关，仿真结果与实验结果均验证了新算法的有效性。本文提出的在线频率响应辨识的新方法适用于任何机电控制系统，从而为从频域角度分析系统控制性能提供了一种途径，同时特有的在线参数辨识技术能自动调节控制器的控制参数，能提高系统的控制效果，但硬件的计算能力可能满足不了某些复杂的在线辨识算法，未来稳定可靠的辨识算法仍然是研究热点。