基于变参数PI控制的双馈风电机组频率控制策略

2019-01-09张俊武王德林潘志豪

电工电能新技术 2018年12期

张俊武，王德林，刘柳，潘志豪

(西南交通大学电气工程学院，四川成都 610031)

1 引言

近年来，风力发电凭借其资源丰富、可大规模开发、建设周期相对较短等优势，迅速发展成为未来可再生能源的主要来源。然而，风电并网容量不断增大给包括频率稳定性在内的电力系统安全稳定运行带来了一系列的挑战[1,2]。为减弱风电并网给电力系统带来的冲击，保证电力系统安全稳定运行，国内外最新发布的一些风电场并网导则均明确要求并网风电场能够主动参与系统频率控制。

双馈风电机组(Double-Fed Induction Generator，DFIG)的转子中储存着大量的旋转动能[3]，但由于利用变频器控制的风电机组转子转速和系统频率是解耦的，DFIG转子动能被完全“隐藏”，不具备响应系统频率变化的能力。为了使DFIG具备与同步发电机类似的频率响应能力，国内外学者对转子动能控制的DFIG频率控制方法的研究已取得丰硕的成果[4-10]，该方法的基本思想是将存储在DFIG转子上的旋转动能转化为电磁功率，通过释放/吸收转子动能改变DFIG输出的有功功率，从而为系统频率控制提供一定的有功支撑。

DFIG虚拟惯性控制的瞬时性使其只能对系统功率提供短时的支撑，然后通过转速恢复回到初始运行状态，为下一次调频做好准备。转速恢复过程向电网吸收有功功率会导致系统频率二次下跌，给系统频率响应带来不利影响[11-13]。为了解决此问题，对DFIG转速主动保护和风电的退出频率控制的深入研究显得尤为重要。文献[14]提出了根据DFIG容量和实时运行工况整定比例-积分系数的定系数PI控制器的转速保护方式，使DFIG随着转子转速下降逐渐退出频率控制过程，对缓解系统频率的短时跌落虽取得一定效果，但仍有一定的功率缺失和频率跌落。由于将风电场中处于不同工况的机组等值为单台风电机组不够准确，因此对风电场调频控制的研究需先对其进行分组，文献[15,16]根据风速进行电场内机组的分组，具有一定的科学性，但忽略了风电场内多数风电机组可能处于同一风速区间的情况，这可能会大大降低优化效果。文献[17]对分组策略进行了改进，但所采用的降级方式对于最低等级无法处理，存在低等级机组数量本来不过低引起的切机。针对DFIG直接转速恢复引起频率二次跌落问题，本文提出一种基于变参数PI控制的转速恢复方案，由于转速恢复初期PI参数较小，不会出现功率的跃变，随着转速恢复的进行PI参数逐渐增大，DFIG逐渐恢复到初始运行状态。对于各风速区间机组数量均匀分布的风电场，给定各机组不同的转速恢复时间，避免同时进入转速恢复环节，缓解系统频率的骤跌；由于各风速区间机组数量分布不均匀的风电场采用延时恢复策略退出频率控制时仍可能有明显的频率骤跌，因此针对风速区间机组数量分布不均匀情况，在变参数PI控制的延时恢复策略的基础上提出风电场优化分组策略，避免了不均匀风电场转速恢复引起的系统频率骤跌。最后，在接入DFIG的3机9节点仿真模型中，通过仿真验证了所提控制方法和策略的正确性和有效性。

2 双馈风电机组转子动能控制

风电调频控制器的原理即在系统频率跌落时降低风电机组转子转速，释放出部分转子动能提供功率支撑，频率控制完成后，应使DFIG机组转子转速恢复到初始运行状态。通常情况下，DFIG运行在最大功率点跟踪(Maximum Power Point Tracking，MPPT)模式以充分利用风能，但为了使风电机组有足够的裕度参与系统频率调节，需要使其在非最大功率点运行为系统频率调节留有备用容量[18]。双馈风电机组普遍采用的转子动能控制方法如图1所示。其中，ωr为转子转速，f为系统实测频率，fN为额定频率50Hz，Kdf、Kpf分别为微分环节和比例环节系数，ΔP为虚拟惯性环节提供的短时功率，Pref为DFIG功率给定值。

图1 双馈风电机组虚拟惯性环节Fig.1 Virtual inertial control of DFIG wind turbines

当DFIG运行于减载模式时，通过图1虚拟惯性附加环节响应系统频率的变化进而改变功率给定值，通过释放/吸收转子动能来改变DFIG的有功输出，参与系统频率调节，该附加环节控制过程短、变化快，能够快速响应电网频率的变化。图2为减载模式下DFIG的功率-转速关系示意图。其中，Pm为风力机输送到双馈感应发电机的机械功率，Popt为减载运行模式下的风力机输送到双馈感应发电机的有功功率参考值。

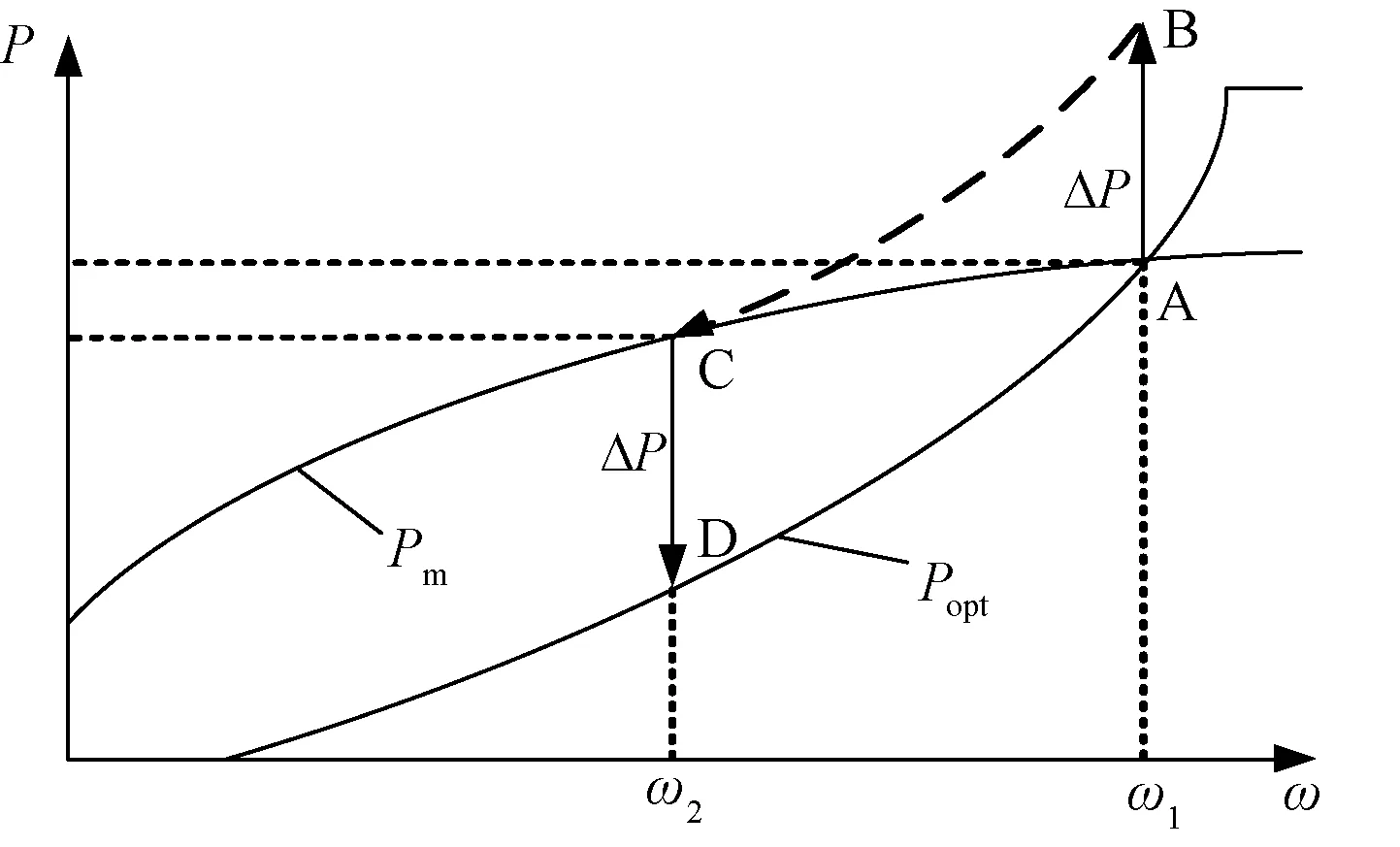
图2 DFIG的功率-转速关系图Fig.2 Relationship between power and rotor speed of DFIG based on wind turbines

根据功率平衡方程，发电机稳定运行时，有：

Pref=Popt=Pm

(1)

加入附加频率控制后，DFIG有功功率的参考值为：

Pref=Popt+ΔP

(2)

假设初始时刻系统功率平衡处于稳定状态，DFIG稳定运行在工作点A(此时ΔP=0，风电不参与调频)，对应转速为ω1。现负荷突然增大引起系统频率减小，DFIG响应系统频率变化降低转子转速释放转子动能，输入功率由A点沿着当前风速所对应的捕获风功率减载曲线减小至D点，输出功率由A点快速增加至B点，并随着转速和输入功率降低而逐渐减小至C点。此时DFIG运行于转速ω2。由于转子动能控制无法长时间参与频率调节，当完成调频后将退出频率控制过程，直接令ΔP=0，使得Pm>Pref=Popt，DFIG进入加速状态，直到转速重新恢复到ω1并稳定运行于A点。由于退出频率控制时转子向电网吸收功率，会使得系统有功功率骤减，进而引起系统频率的二次跌落，不利于系统频率稳定。图3和图4分别为突增负荷时系统频率响应曲线和DFIG有功-转速动态响应曲线。

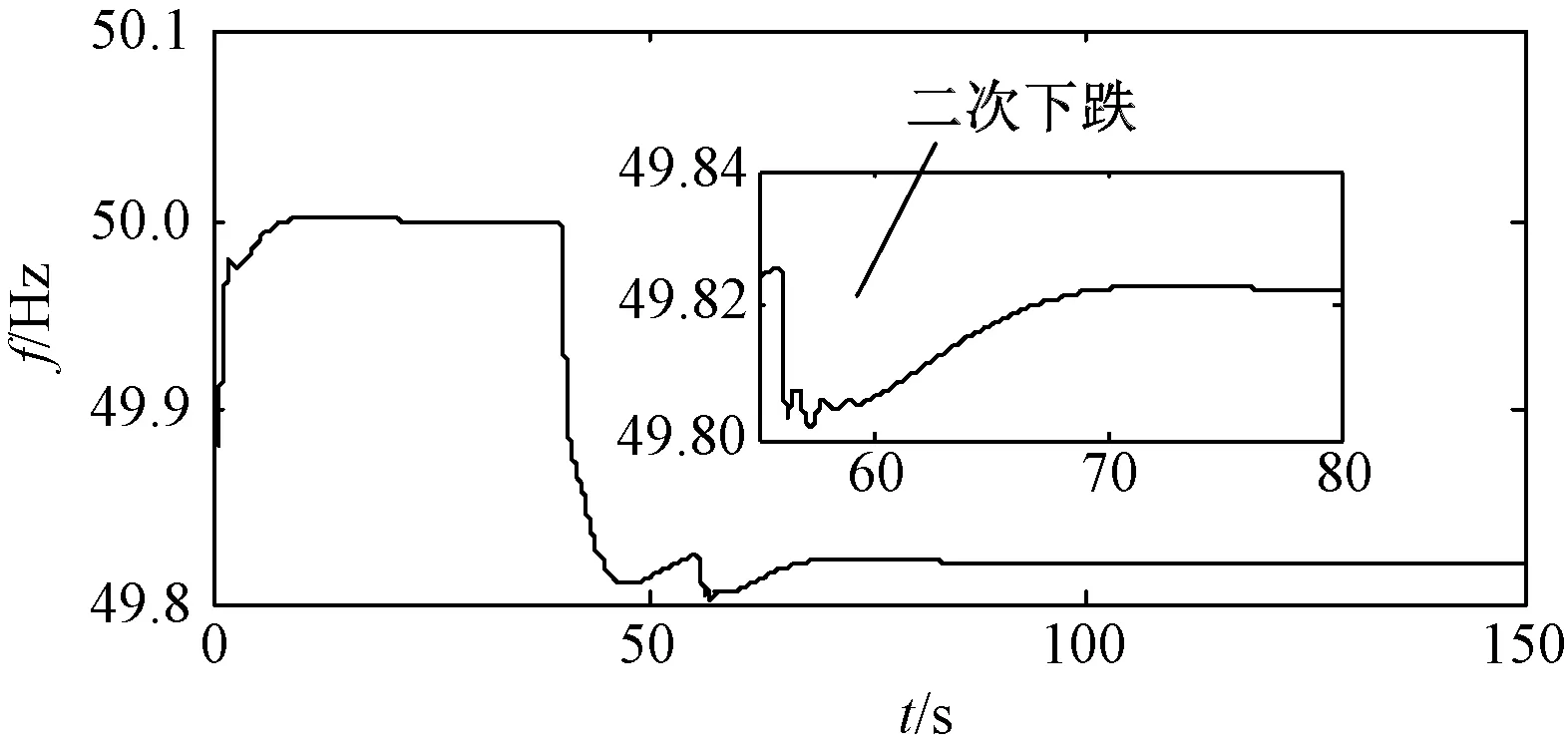
图3 系统频率响应曲线Fig.3 Curve of system frequency response

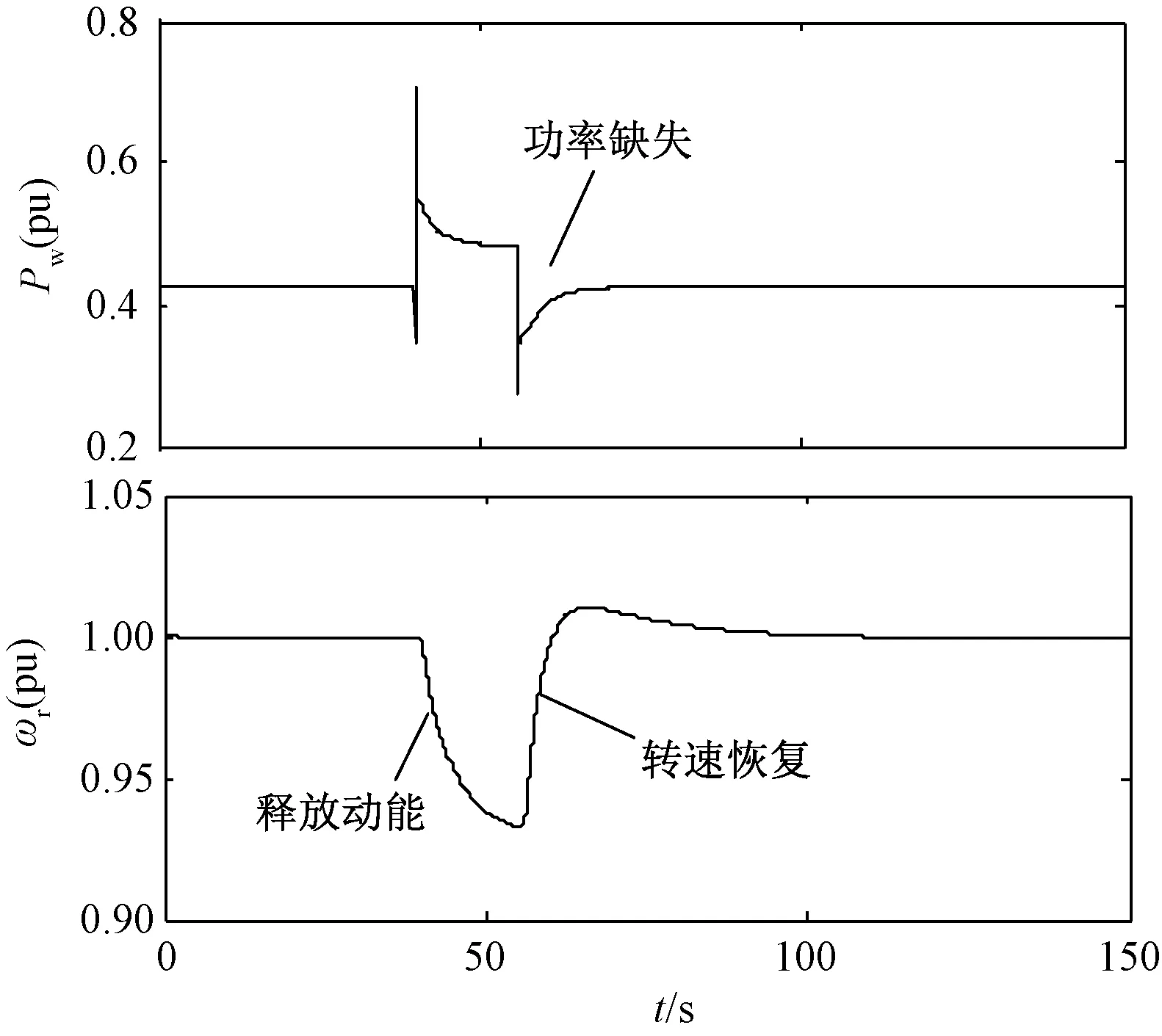
图4 DFIG功率和转速响应曲线Fig.4 Dynamic response curve of DFIG wind turbines

从图3和图4可以看出，当系统负荷增大时，引起频率的下降，转子动能控制通过降低转速释放转子动能向系统提供短暂的有功功率支撑，当风电机组释放转子动能后，转子进入加速状态以快速恢复到初始运行状态，由于该过程要向电网吸收能量，会引起DFIG有功功率的缺失和系统频率的二次下跌。

3 改进的虚拟惯性控制和基于变参数PI控制器的转速恢复方式

针对转子动能控制的DFIG直接转速恢复退出频率控制引起系统有功功率缺失和系统频率二次跌落问题，对转子动能控制进行改进。改进方案的基本思路为：系统频率下降时，DFIG通过释放转子动能为系统提供频率支撑，一定时间后DFIG退出频率控制，通过基于变参数PI控制器的转速恢复环节逐渐恢复到最优转速。与固定参数不同，变参数PI控制器在转速恢复过程中逐渐调整控制器比例-积分系数，利用负反馈作用使风电机组随转速逐渐下降退出频率控制。图5为本文改进的虚拟惯性和转速恢复控制结构总图。其中，ωr为风电机组实时转速，ωref为某风速下风电机组转速给定值，Kp、Ki为PI控制器可变参数， ΔP1为转速恢复环节输出功率；Protect为转速保护环节，Recover为转速恢复动作模块。

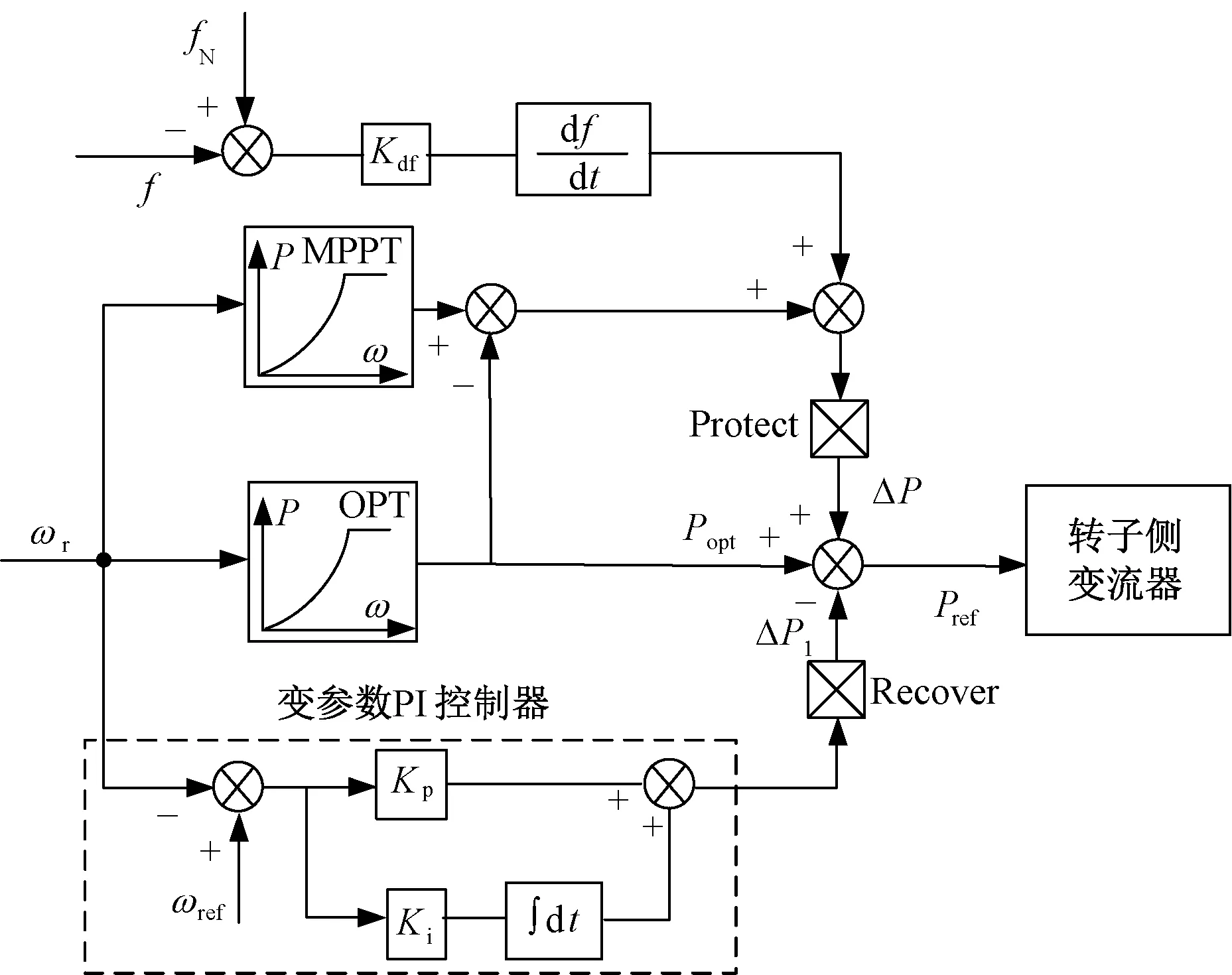
图5 改进的虚拟惯性控制和转速恢复模块控制结构总图Fig.5 Model of improved virtual inertial control and rotor speed recovery control

3.1 虚拟惯性环节

在DFIG减载运行模式下，结合风电场可增发的最大有功功率同时使DFIG能够响应系统频率变化，将虚拟惯性附加功率ΔP设定为：

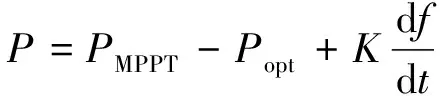
(3)

式中，PMPPT为最大功率追踪运行模式下风力机输送到双馈感应发电机的有功功率参考值。将式(3)作为虚拟惯性控制附加功率的优点在于：

(1)能充分利用DFIG快速暂态响应能力，为常规机组调节稳态频率起到支撑作用。

(2)使得不同风况的DFIG获得有差别的功率参考值，同时能够充分利用风电机组备用容量，提高风能利用率。

(3)由于该值为DFIG减载功率，因此不会出现转速过低引起的切机情况。

3.2 转速保护模块

DFIG通过虚拟惯性控制降低转速释放转子动能参与调频时，当转速低于ωmin通常直接将机组增发有功降为零，使DFIG不再参与系统频率控制，避免转速超出安全运行范围。转速保护模块的输出信号满足：

(4)

式中，Protect为“0”表示不动作转速保护模块；Protect为“1”时触发该模块开始动作；ωmin取值为0.7pu。上述方式存在的问题在于：触发转速保护信号时，DFIG有功出力瞬时降低可能引起频率二次跌落，不利于机组安全运行，同时影响系统频率稳定性。

为了达到转速保护的目的，同时避免功率骤降，将变PI参数控制器引入其中，当风电机组转子转速下降至下限值ωmin时，将调频功率控制信号ΔP随转速逐渐减小至零，DFIG逐渐退出频率控制过程，避免系统有功功率骤降，从而避免系统频率的骤跌。

3.3 基于变参数PI转速恢复模块

为了保证机组的安全运行，风电机组通过降低转子转速短时增大有功输出后，需要进行转子转速恢复，通过引入变参数PI转速恢复避免频率的二次跌落。其中，变参数时段比例环节Kp、积分环节Ki曲线斜率分别为a(固定为0.005)、b(随m变化)，Kp、Ki表达式如式(5)、式(6)所示，变化参数曲线如图6所示。

(5)

(6)

式中，ts为转速恢复开始时刻(也是参数开始变化的时刻)；m为时间常数。

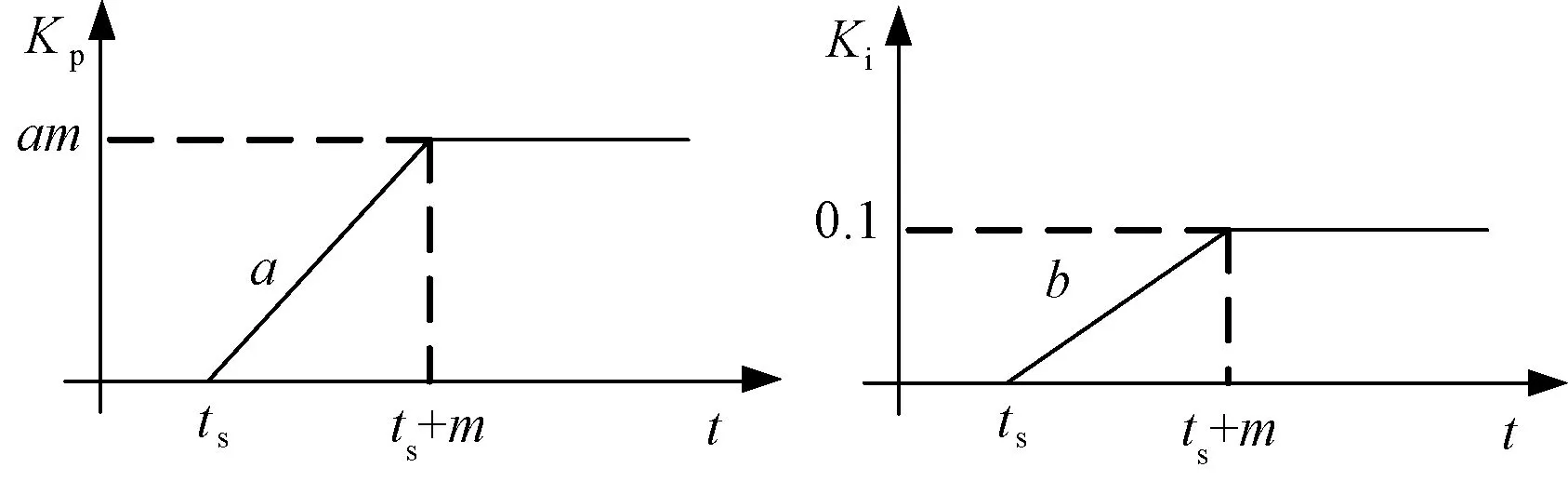
图6 Kp、Ki变化参数曲线图Fig.6 Curve of variable parameter Kpand Ki

转速恢复动作模块的输出信号应满足：

(7)

式中，Recover设置为“0”表示转速恢复模块不动作；Recover为“1”时触发该模块开始动作。加入变参数转速恢复环节后，风电机组输出功率为：

触发转速恢复模块后，由于初期Kp、Ki值较小，故而不会引起ΔP1的跃变，Kp、Ki随着时间逐渐变大，转子转速偏差通过变参数PI控制器逐渐被消除，DFIG恢复至初始运行状态，为下次频率控制做好准备。

4 风电场转速延时恢复及优化分组策略

4.1 风电场转速延时恢复策略

现有对风电场转速恢复调频控制的研究往往将风电场等值为一台DFIG。对于拥有几十台甚至上百台DFIG的大型风电场，由于各风电机组所处的风况不同，运行状态均有差异，这时将整个风电场等值为一台DFIG是不精确的，如果同一时刻所有机组都进入转速恢复模式，其提供的有功功率同时减少可能导致系统频率的二次跌落[19]。

本文对于各风速段内风电机组数目相当(也称作风电机组均匀分布)的情况引入变参数PI控制器，向各风电机组下发参考功率值时需考虑时间差异，使得不同风况风电机组获得有差别的功率参考值及转速恢复时间。首先确定第1组的转速恢复时刻ts1，其他机组在前一台机组基础上增加Δt。根据设置延时使不同工况的风电机组获得不同的转速恢复时刻，不同风速等级的风电机组会在不同时刻依次退出有功增发阶段，避免所有机组功率同时下降和恢复，减少转速恢复对于有功支撑的削弱，从而保证风电机组增发有功值获得优化，同时避免系统频率的二次跌落。

4.2 风电场优化分组策略

本文对于大多数风电机组处于同风速等级(也称作风电机组分布不均匀)的情况，它们将获得同样的转速恢复时间信号，引起频率的二次跌落。为了避免该情况的发生，将风电厂内风电机组进行内部分组十分必要。因此提出一种基于风速的优化分组策略。主要包括以下原则：

(1)根据计算，1.5MW的双馈风电机组在风速7m/s时，转子的最优转速为0.7pu。为了保留足够的安全裕度，仿真中定义风速8m/s为风电机组参与调频的最低风速，低于8m/s不参与系统调频。

(2)根据机组实际所处风况，将风电机组按照风速段均匀地划分为若干组。在确定分组数量时，若分组过少，大量风电机组存在于同一组的可能性较大，分组意义难以体现且效果不佳。分组过多会延长恢复过程时间，进而延长DFIG参与频率控制周期，不能及时做好下次参与系统频率控制的准备。综合以上两方面因素，可将风速8m/s以下设定为1个等级，8～12m/s的机组按每间隔1m/s设为4个等级，高于12m/s为一个等级。

(3) 风电场优化分组流程如图7所示。若存在某一等级内风电机组数量超过全部参与调频机组数量的一定比例η(本文假设η=40%)，则在该等级内部进行均匀分组，直到每组所占比例低于η为止。

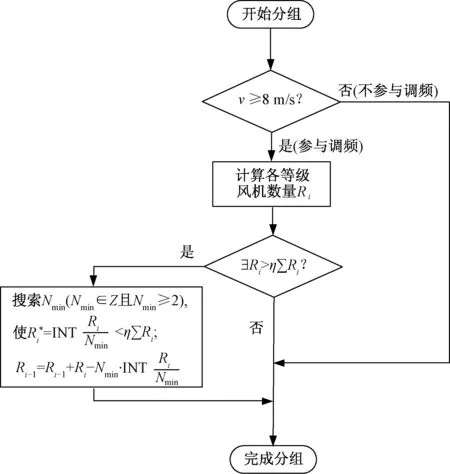
图7 风电场优化分组流程图Fig.7 Grouping optimization flowchart for wind farms

5 仿真分析

本文基于MATLAB/Simulink仿真平台建立了含风电并网仿真模型，如图8所示。该仿真模型将经典3机9节点模型的母线1处的同步机用DFIG代替。同步机G1、G2额定容量均为300MW，虚线部分等值风电场共由200×1.5MW的双馈机组共同构成(渗透率50%)。单机情况时，先将风电场等值为一台DFIG(超速减载20%运行)，通过对单机情形的仿真，验证了基于变参数PI控制器转速恢复环节对系统频率的改善效果。多机情况时，将风电场分组等值为三台DFIG(均超速减载20%运行)，通过对多机情形的仿真，验证风电场转速延时恢复策略和优化分组策略的有效性。

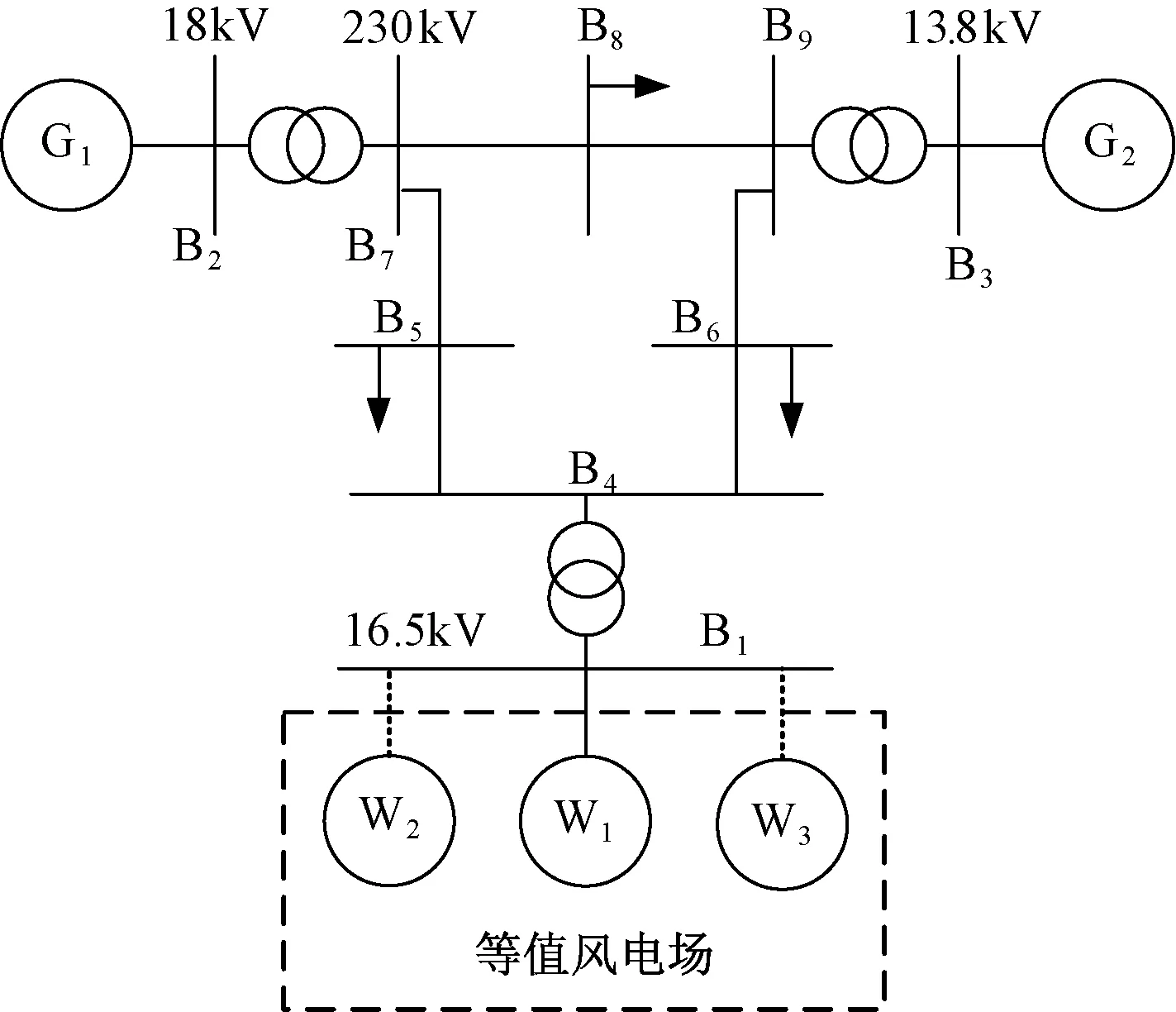
图8 含风电机组3机9节点仿真系统模型Fig.8 Simulation model of three machines nine buses system

5.1 单机情况

为了体现基于变参数PI控制器转速恢复环节对系统调频的改善效果和选择控制器变参数时间常数m的合理性，对单机情况做了以下仿真。

5.1.1 不同转速恢复方式仿真对比

仿真时，风电机组风速为9m/s，仿真系统初始频率为50Hz，在40s时突增50MW负荷，虚拟惯性环节作用15s后触发转速恢复开始信号，分别采用直接转速恢复方式、基于定参数PI控制转速恢复和基于变参数PI控制转速恢复进行仿真，得到3种转速恢复方式下系统频率响应曲线，如图9所示。双馈风电机组功率和转速响应曲线如图10所示。

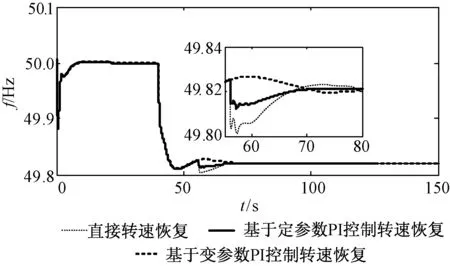
图9 3种转速恢复方式下系统频率响应Fig.9 System frequency response of three kinds of speed recovery mode

图10 双馈风电机组功率和转速响应曲线Fig.10 Power and speed response of DFIG based wind turbines

从图9和图10可见，直接转子转速恢复方式在转速恢复初期转子转速立即加速上升，但总的恢复时间却没有缩短，且出现一定超调，进而引起短时有功功率0.13pu的缺失，导致系统频率二次跌落0.03Hz。实际系统中，对于不同的情形可能对系统功率和频率的影响更大。采用基于定参数PI控制器时转子转速恢复速度有所减缓，虽减小了有功功率的短时缺失，但也会引起0.1pu的有功骤减。采用基于变参数PI控制时转子转速逐渐恢复至最初状态，避免了转速恢复时刻功率突变，同时缩短了恢复至初始状态的时间，且不会出现系统频率的二次下跌。

5.1.2 不同m值的变参数曲线

为了进一步说明不同m值对DFIG频率控制的影响，验证m值的合理选择范围，设定Kp、Ki变化参数部分曲线斜率a=0.005。分别对m取6s、16s、30s三种不同情形进行了仿真。Kp、Ki变化参数曲线图如图11所示。不同m值时系统频率响应、双馈风电机组功率和转速响应曲线分别如图12、图13所示。

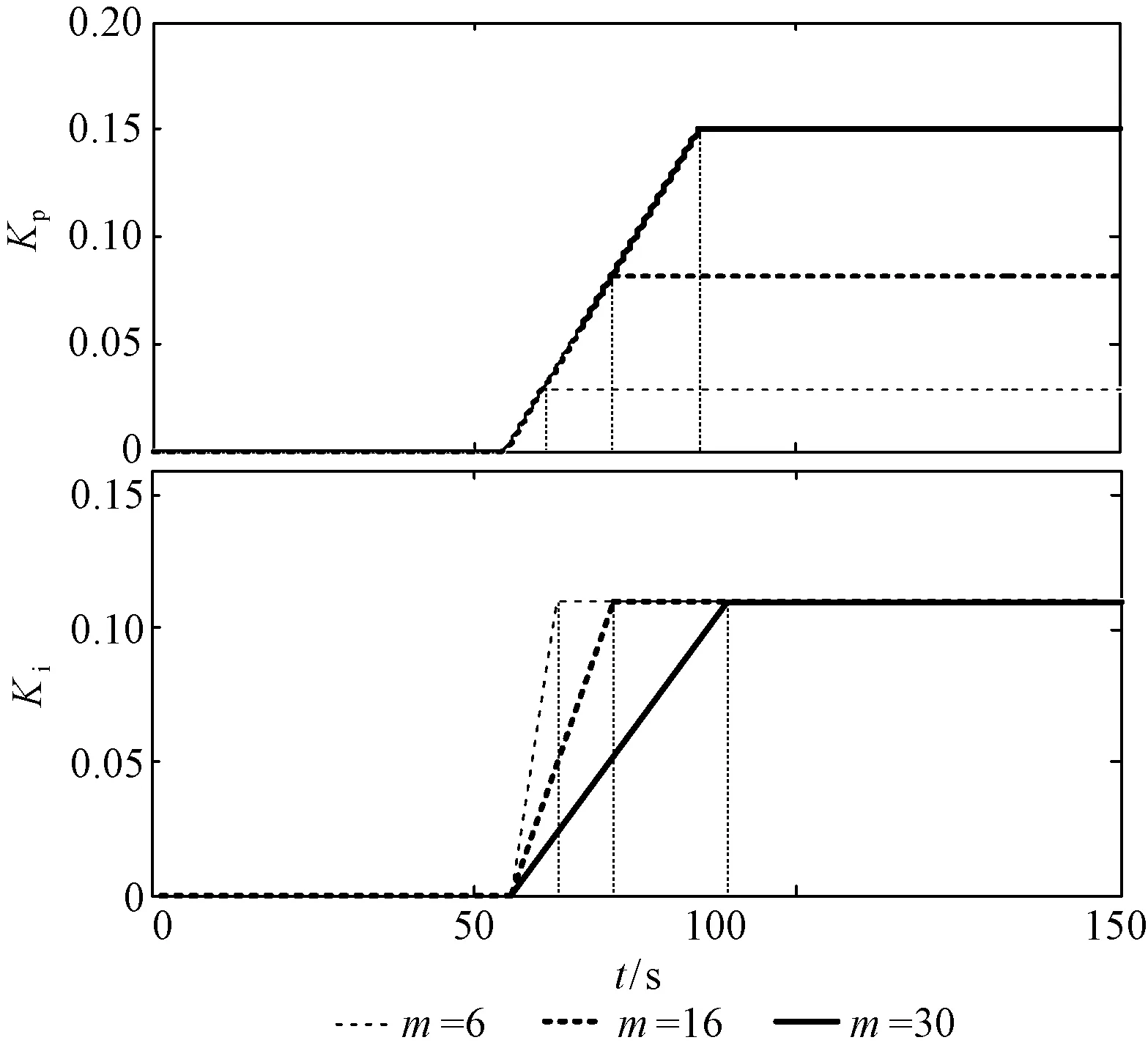
图11 变参数Kp、Ki曲线Fig.11 Curve of variable parameter Kp and Ki

图12 不同m值系统频率响应Fig.12 System frequency response under different m value

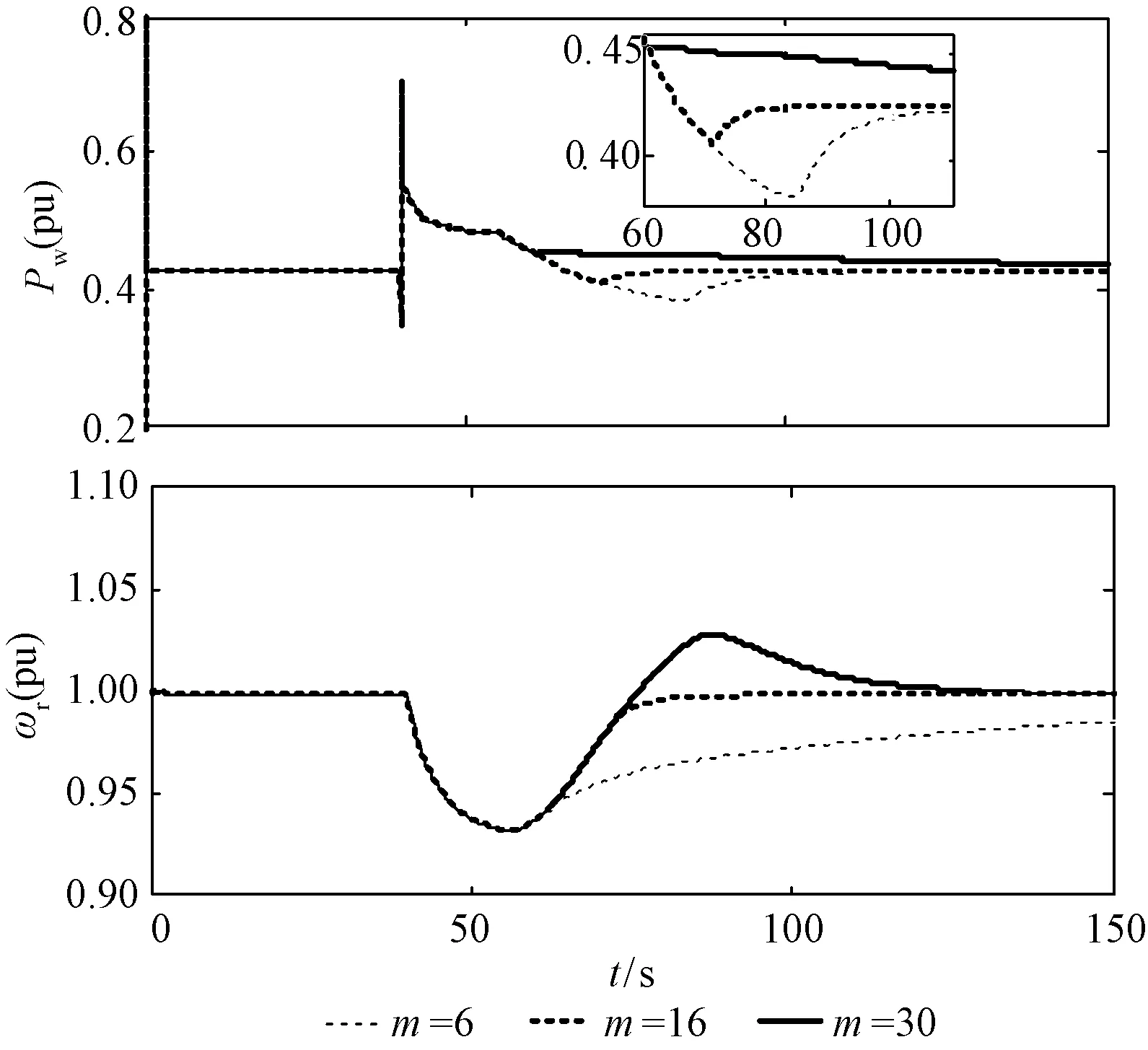
图13 不同m值双馈风电机组功率和转速响应曲线Fig.13 Power and speed response of DFIG wind turbines under different m value

从图11可知，不同的m值直接影响Kp的最大值和Ki的斜率。m值越大，Kp最大值越大，同时Ki斜率越小，反之同理。从图13可知，不同的m值影响双馈风电机组的转子转速恢复时间，m太大或太小都不利于双馈机组恢复到初始状态。不同m值下双馈机组恢复时间见表1。

表1 不同m值下双馈风电机组恢复时间Tab.1 DFIG recovery time under different m values

从表1可知，m=16s时转速恢复时间只需25s，而m=6s或m=30s时转子转速恢复时间均大于130s。因此，m值的合理选取有利于系统的平稳恢复。大量仿真验证表明，为了保证转速恢复时间在40s内，m的取值介于14～18s为宜。

5.2 多机情况

为了体现转速延时恢复策略和优化分组对风电场在系统频率跌落方面的改善效果，对多机情况做了以下仿真。

5.2.1 各风速区间机组数量分布较均匀

风电机组均匀分布时各功率控制等级的风电机组台数见表2。分别针对风电场同时直接转速恢复、延时直接转速恢复和基于变参数PI控制延时转速恢复进行仿真。仿真时，系统70s突增50MW负荷，转速恢复开始时间ts1=85s，延迟时间Δt=3s，系统频率响应如图14所示。

表2 不同风速区间对应DFIG机组数量Tab.2 Number of DFIG units corresponding to different wind speed range

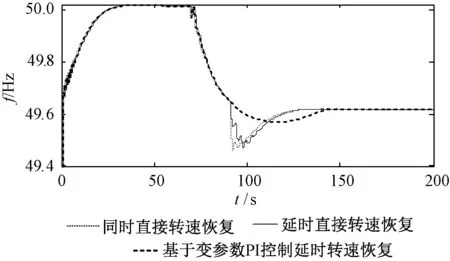
图14 风电机组均匀分布不同转速恢复方式频率响应Fig.14 Frequency response in different speed recovery mode with well-distributed wind turbines

从图14可知，风电机组均匀分布时，同时直接进行转速恢复将会引起系统频率的二次跌落，最低值已达49.5Hz以下，严重影响了系统的稳定运行。延时直接时转速恢复方式虽放缓了频率跌落的态势，但仍然呈阶梯状，在短时间内频率骤减0.15Hz，基于变参数PI控制延时转速恢复能平滑过渡风电机组退出引起的系统有功功率的缺失，系统频率逐渐恢复至稳定状态，利于系统的稳定运行。

5.2.2 各风速区间机组数量分布不均匀

风电场内多数风电机组处于同等级风速区间时，风电机组将会同时退出频率控制。针对此种情况需先对风电厂内部进行优化分组。风电机组分布不均匀时，优化分组前各风速等级的风电机组台数见表3。此时绝大多数风电机组处于9～10m/s风速段，风电场渗透率η=57.5%>40%，因此需先根据本文所提优化分组策略对其进行优化，优化结果见表4，其中N为均分待优化区间DFIG数量时的风速值。为体现优化效果，分别就风电场基于变参数PI控制延时转速恢复分组优化前后对比仿真，仿真时系统70s突增50MW负荷，系统频率响应如图15所示。

表3 优化前不同风速区间对应DFIG机组数量Tab.3 Number of optimization of different wind speed interval corresponding to DFIG wind turbines

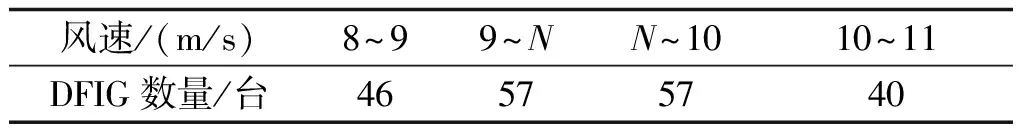
表4 优化后不同风速区间对应DFIG机组数量Tab.4 Number of different optimized wind speed range corresponding to DFIG wind turbines

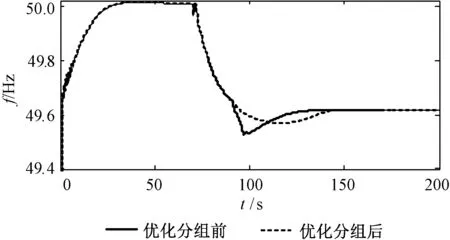
图15 优化分组前后系统频率响应曲线Fig.15 System frequency response curve of whether or not use the optimization grouping

从图15可知，优化分组前，由于同一风速等级的风电机组数量过多，基于变参数PI控制延时转速恢复虽已能减缓系统频率的骤减，但在5s时间内系统频率下降0.08pu，下降趋势依然明显。分组优化后避免了同一时间大多数风电机组同时退出的情况，虽延长了系统频率恢复稳定的时间，但明显减缓系统频率的跌落，使系统在发生负荷扰动时，平稳地过渡到稳定状态，有利于系统的安全稳定运行。