特高压自耦变压器直流偏磁无功损耗算法研究

杨培宏， 李 亚， 亢 岚， 冯士伟

(1. 内蒙古科技大学信息工程学院， 内蒙古 包头 014010；2. 内蒙古科技大学矿业与煤炭学院， 内蒙古 包头 014010)

1 引言

高压直流输电单极或双极不对称运行时所产生的入地电流与地磁扰动所产生的地磁感应电流均会导致变压器发生直流偏磁现象，将会导致变压器励磁电流畸变且伴随有高次谐波的出现、无功需求增多、变压器噪声和振动增大等一系列问题，严重影响电网及其主要电力设备的安全稳定运行[1-3]。发生于1989年5月13日的加拿大魁北克大停电事故，其主要原因就是地磁感应电流导致变压器无功损耗增大，各次谐波的增加导致电容器组被迫退出从而致使735kV超高压电网电压崩溃，造成了严重的经济损失[4-6]。21世纪以来，我国发现了多起直流偏磁电流侵害电网的事件。广东岭澳核电站中500kV变电站在2004年11月10日监测到变压器中性点的地磁感应电流为75.5A。随着我国直流输电工程的建设，为满足长距离输电的需求，1000kV特高压电网正在逐步投入使用。且对1000kV电网，其地磁感应电流的计算值高达382.9A[7]。同时，由于其体积较大且为便于运输，1000kV特高压变压器为单相自耦变压器，通常是将三个单相特高压自耦变压器组成三相变压器组投入使用，从而导致三个变压器的磁路相互独立，其偏磁磁通不能相互抵消。因此，直流偏磁电流对特高压变压器有着极大的影响。

国内外研究直流偏磁电流对变压器的影响主要是利用相关理论、算法来实现的。国外的研究方法主要指将铁心材料的磁化特性曲线等效为两段线性曲线，并利用相关的电磁理论进行分析，其分析结果发现流入变压器的直流偏磁电流与其无功功率损耗近似成线性关系，其大小主要取决于直流偏磁电流的大小、变压器电压等级、铁心电抗大小[8]。文献[9]通过建立单相四柱式特高压自耦变压器的磁-电路耦合模型，以此来计算直流偏磁下变压器的励磁电流特性与无功损耗特性，计算结果表明直流偏磁电流与三相无功损耗近似呈线性关系，比例系数为2.44。文献[10]利用特高压变压器的实际参数，通过有限元分析其场-路耦合模型，进行迭代计算。结果表明，当直流偏磁电流超过一定范围后，无功功率随着直流偏磁电流的增加近似呈线性关系。文献[11]则是利用特高压变压器厂家所提供的U-I曲线，经过相应的转化与计算，计算地磁感应电流影响下变压器无功扰动的增量，为大规模电网的地磁感应电流无功扰动工程计算提供相应的参考依据，但是此方法忽略了漏磁对计算结果的影响。对于我国自主研发的单相四柱式特高压自耦变压器，国外相关专家学者并未对此做相应的研究，而国内的研究主要集中于电、磁相结合的分析，并未在电磁暂态环境当中研究特高压变压器的直流偏磁特性。

笔者利用PSCAD/EMTDC仿真软件针对我国自主研发的单相四柱式特高压自耦变压器建立了电磁仿真模型。模型中变压器的建立主要依据其中的统一电磁等效电路 (Unified Magnetic Equivalent Circuit， UMEC)变压器模型，该模型不仅能模拟变压器铁心的非线性，还能考虑到变压器结构的特殊性。因此，笔者利用此模型计算直流偏磁下，特高压变压器的励磁特性与无功损耗特性，为治理特高压电网的无功波动提供一定的参考依据。

2 变压器直流偏磁无功损耗数学模型

直流偏磁下变压器铁心磁链与励磁电流的非线性特性曲线如图1所示。其中ψ0为正向磁链的峰值，ψknee、ψdc分别为拐点磁链、直流偏置磁链，Lm为变压器励磁感抗，Lair-core为变压器空心感抗，L0为等效线性感抗，I0则为正向励磁电流，Δψ为磁链增量，ΔI为励磁电流增量。当直流偏磁电流从中性接地点进入变压器后，将会产生直流偏置磁链ψdc，从而导致变压器磁链向上偏移，变压器进入半波饱和状态，此时变压器等效电抗减小，进一步导致无功损耗增加，计算方法[8]如下。

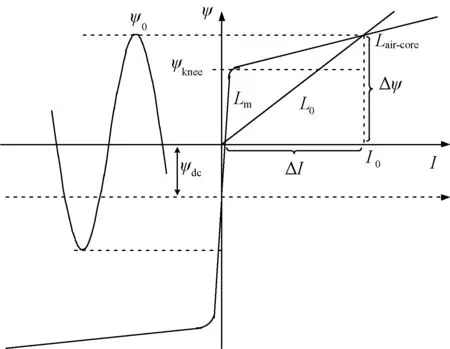
图1 直流偏磁下磁链与励磁电流的非线性特性曲线Fig.1 Flux linkages versus exciting current nonlinear characteristic with DC flux offset

基于电磁感应定律，电压有效值到磁链的转换如式(1)所示，据此可求得空载情况下变压器所施加电压与磁链的关系：

(1)

(2)

式中，U0为变压器所施加正弦电压有效值；ω为电源角频率。

从图1可以看出，变压器铁心磁通半波饱和时，变压器励磁感抗Lm远大于变压器空心感抗Lair-core，因此，等效线性电抗L0可由Δψ、ΔI求得。

(3)

由于变压器直流偏磁时，励磁电流发生畸变，且波形会向上(或向下)移动，因此导致励磁电流负半周(或正半周)的幅值几乎为零。此时，变压器铁心有效线性感抗可由式(4)给出。

Leff=2L0

(4)

忽略磁滞和涡流损耗，变压器等效无功损耗如式(5)所示。

(5)

式中，Q为变压器等效无功损耗；U为电压有效值；Xeff为变压器铁心有效线性感抗。

由式(3)～式(5)可得：

ψdc-λ)

(6)

式中，当给定工作电压U0时，λ为常数。

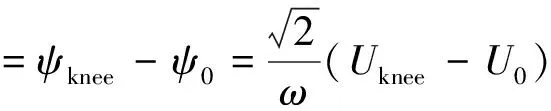
(7)

式中，Uknee为拐点等效电压有效值。直流偏置磁链ψdc的计算如式(8)所示，其中Idc为直流偏磁电流。

ψdc≈LmIdc

(8)

因此，直流偏磁下变压器无功损耗与直流偏磁电流的关系可表示为：

Q=KIdc+C

(9)

式中

(10)

从式(9)可以看出，直流偏磁下变压器无功损耗与直流偏磁电流近似为线性关系。

3 特高压自耦变压器的UMEC仿真模型

3.1 特高压自耦变压器建模

由于变压器的统一电磁等效电路模型(UMEC)不仅能模拟变压器铁心的饱和特性与磁滞特性，而且在模型的分析求解过程中还能够考虑到变压器电路与磁路的耦合关系[12-15]，因此，笔者利用PSCAD中的UMEC变压器模型建立仿真模型。

其中，变压器铁心的饱和特性是利用厂家所提供的I-U曲线来模拟实现的。即在模型参数设置过程中，从厂家所提供的I-U曲线中选取10个点的I、U值作为模型的输入参数，将表示变压器铁心饱和特性的曲线用多斜率分段线性曲线来代替，并利用插值法进行计算，此方法不仅减少了矩阵倒置计算并提高了计算精度。依据特高压变压器的实际绕组结构，需将单相三绕组UMEC变压器模型中两绕组侧的两个绕组首尾相连，形成串联绕组和公共绕组，此外，还需对相关参数进行换算与设置。据此，可建立特高压自耦变压器模型。

3.2 仿真模型介绍

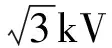
通过分析变压器直流偏磁的原因可知：建立变压器直流偏磁仿真模型的关键在于模拟变压器铁心的磁化特性曲线。因此，为验证所建模型的合理性与正确性，现比较基于UMEC模型的特高压自耦变压器的I2-U曲线与实际I1-U曲线，如表1所示，由表1可知实际值与仿真值最大误差为6.86%，即所建模型的I-U曲线与实际值基本相同。因此，利用PSCAD所建立的UMEC特高压自耦变压器模型可用于研究直流偏磁下变压器的励磁特性与无功损耗特性。

依据特高压自耦变压器的实际运行方式发现，其通常是三台单相自耦变压器组成的变压器组投入运行的，因此其联结方式为YN，a0，d11，如图2所示。高压侧连接额定电压等效电源，中压侧空载或额定负载运行；三相自耦变压器组低压侧为角型连接且与高压、中压绕组中并无“电”的联系，因此重点仿真直流偏磁对变压器励磁特性的影响以及为保证空载与负载运行情况下变量唯一，减少其他因素对仿真结果的影响，在仿真计算过程中低压绕组状态保持不变，即低压绕组开路。而直流偏磁电流则通过在中性点添加直流电势来实现。由于特高压自耦变压器具有电压等级高、高磁导率和小电阻等特性，仿真计算过程中极易导致计算结果发散[16]。因此需在直流电势连接处添加一定阻值的电阻来保证计算结果的正确性与稳定性。依据引言中所提到的1000kV电网中地磁感应电流的计算值高达382.9A，因此，在扩大仿真结果裕度的基础上，将中性点最大偏磁电流设置为450A。

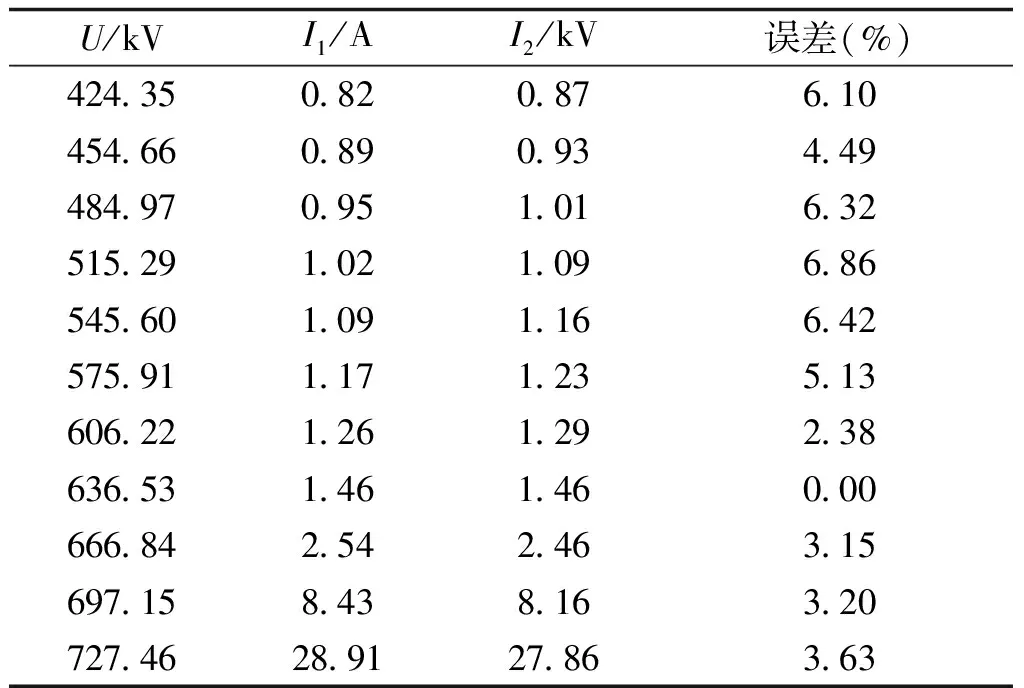
表1 变压器非线性曲线的一致性Tab.1 Consistency of nonlinear curve for transformers

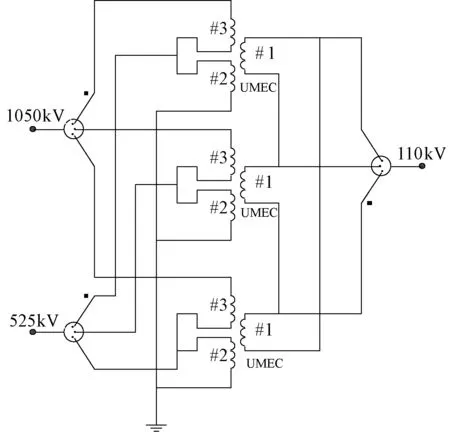
图2 基于UMEC的自耦变压器模型Fig.2 Autotransformer model based on UMEC

4 结果分析

4.1 特高压变压器励磁特性

利用上文中所建立的特高压变压器模型，由于三相变压器组模型中的三台特高压变压器模型具有相同的非线性特性，因此本节只针对其中一台变压器进行励磁特性分析。单台变压器中的直流偏磁电流用Idc来表示。因此，当Idc分别为0、1A、5A时特高压变压器的励磁电流波形与谐波变化分别如图3～图5所示。

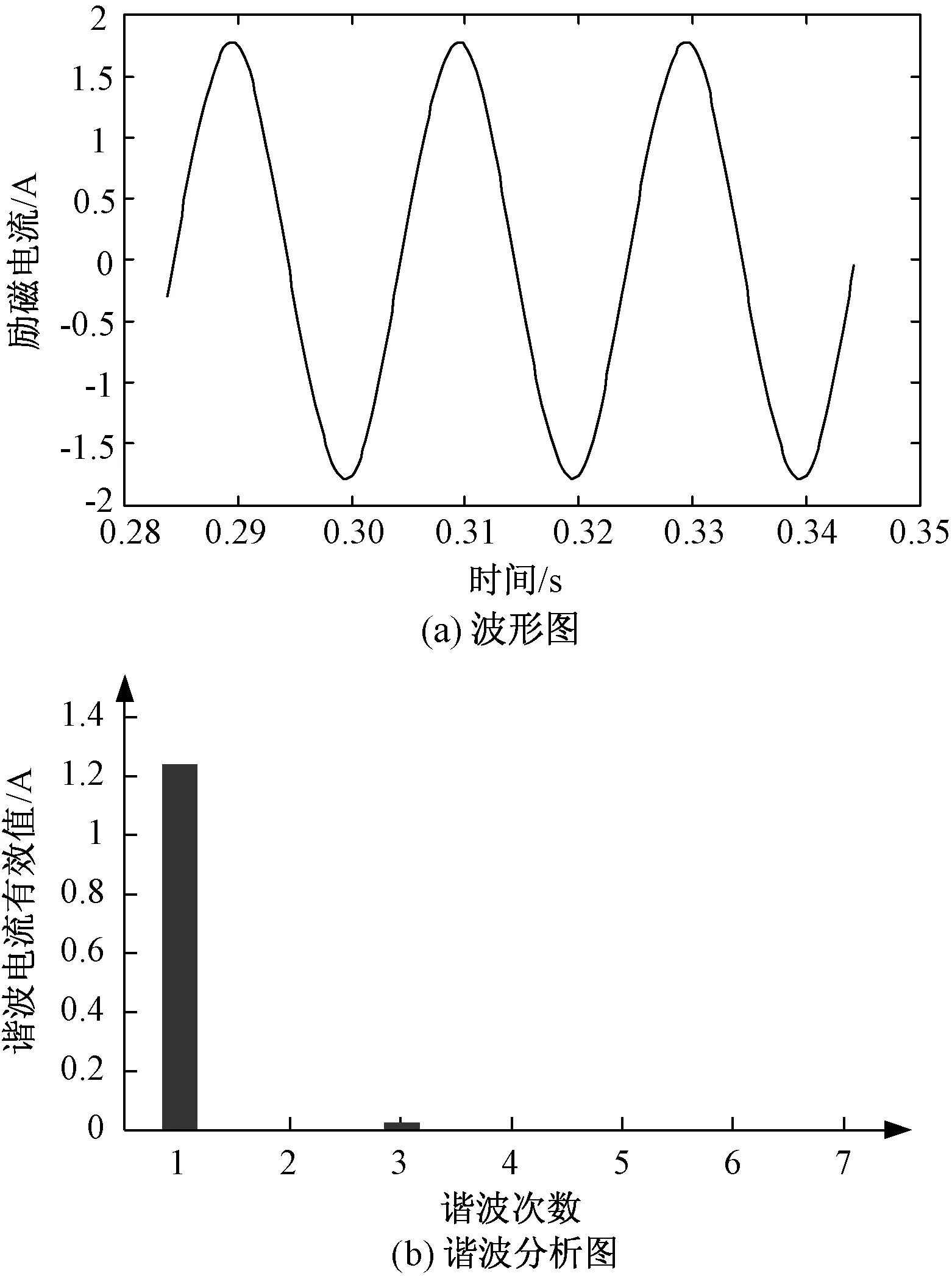
图3 无偏磁时变压器励磁电流及其谐波分析图Fig.3 Exciting current and harmonics distribution of transformer without DC bias current

图4 直流偏磁电流为1A时变压器励磁电流及其谐波分析图Fig.4 Exciting current and harmonics distribution of transformer under DC bias current of 1 A

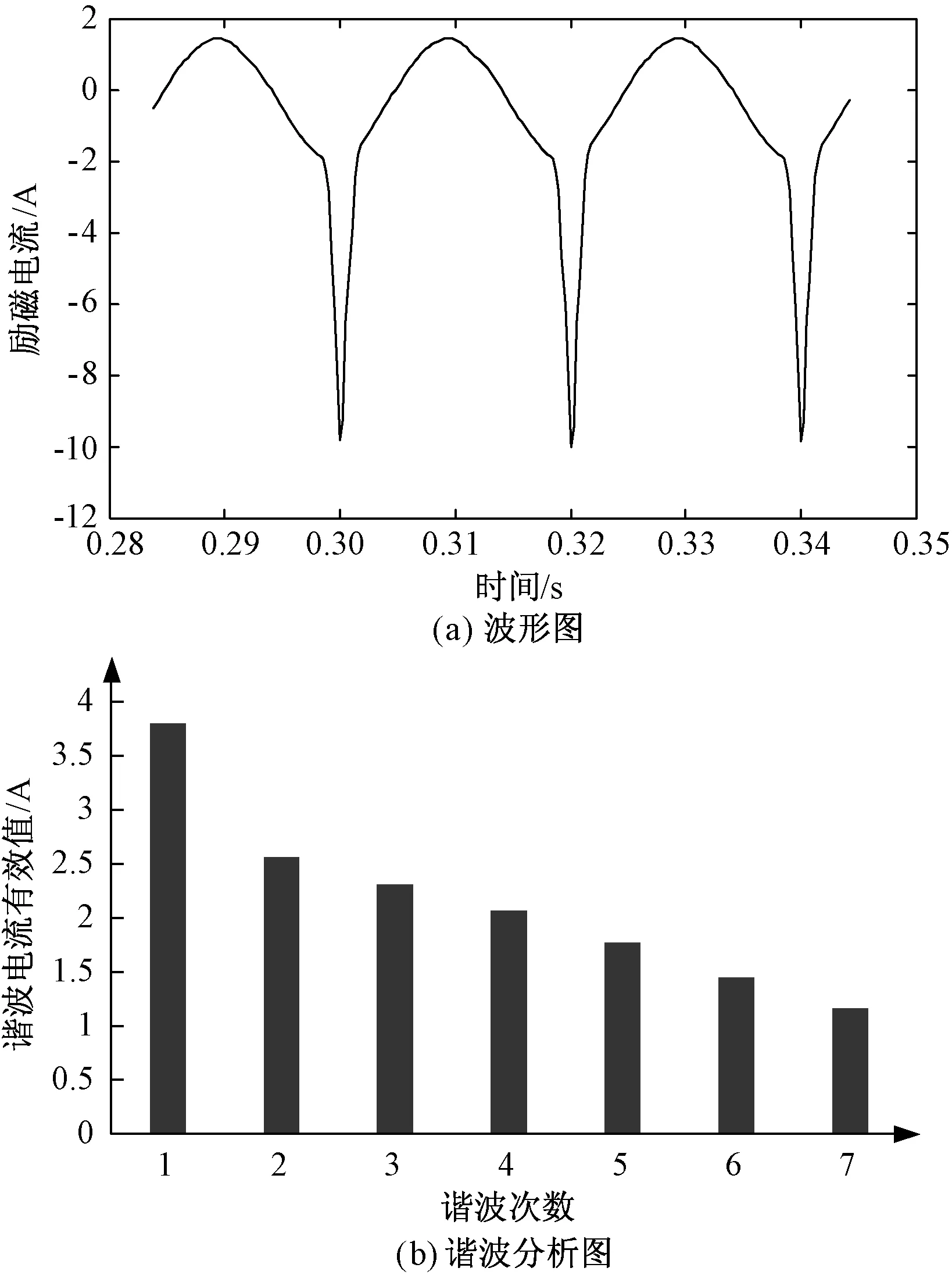
图5 直流偏磁电流为5A时变压器励磁电流及其谐波分析图Fig.5 Exciting current and harmonics distribution of transformer under DC bias current of 5A

从图3～图5可以看出，随着所加直流偏磁电流的增大，励磁电流会向负方向移动，且正向峰值逐步减小，当直流偏磁电流增大到一定程度后，正向峰值会逐步接近于零。此外，随着直流电流的增大励磁电流畸变越来越严重，其各次谐波幅值也在不断地增加，进而导致变压器无功损耗增加。且谐波次数越高，增长越缓慢。

4.2 空载无功损耗计算与分析

依据所建立的UMEC特高压变压器组模型，其高压侧额定电源，中、低压侧空载情况下，逐步增大直流偏磁电流，特高压变压器无功损耗(三相)如表2所示。

表2 空载偏磁条件下无功损耗仿真结果Tab.2 Simulation results of reactive loss under no-load bias conditions

针对表2中的数据，利用MATLAB进行拟合，可得直流偏磁电流与无功损耗之间的关系如图6所示，对图6的曲线进行拟合处理得到式(11)的方程。

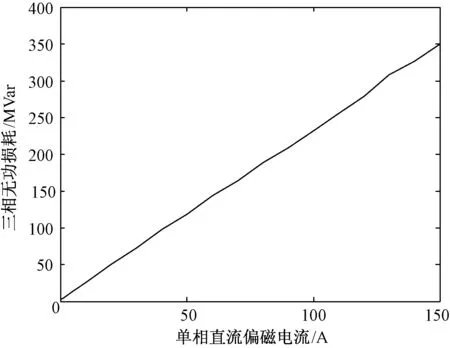
图6 直流电流与无功损耗之间的关系Fig.6 Corresponding relationship between dc current and reactive loss

(11)

式中，2.31为直流偏磁下无功损耗与直流偏磁电流之间的比例系数。可以看出，Q与Idc之间呈线性关系。

4.3 额定负载无功损耗计算与分析

结合3.2节中的空载无功损耗仿真计算，给中压侧添加额定负载，保持其他条件不变，测量结果如表3所示。

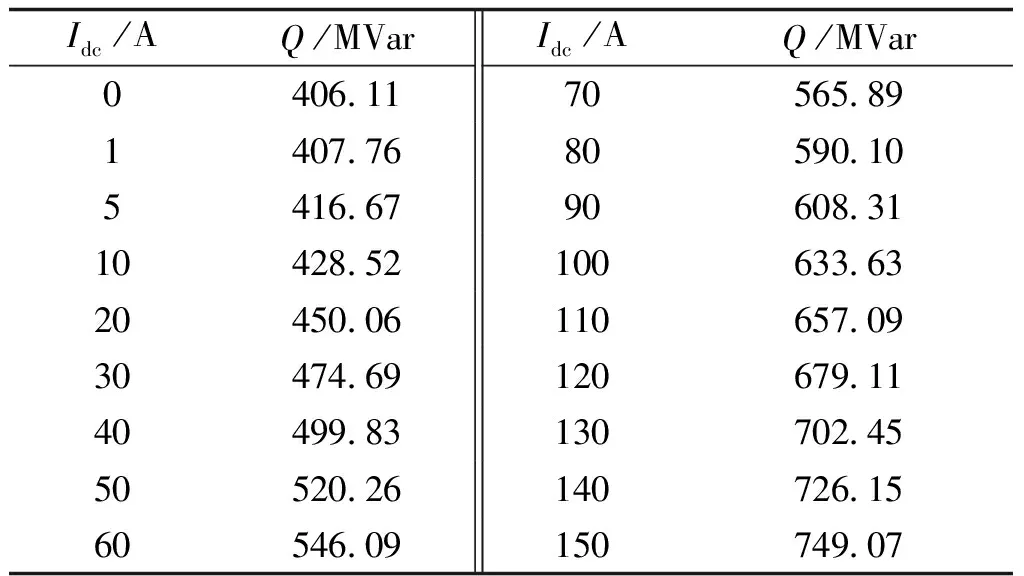
表3 额定负载偏磁条件下无功损耗仿真结果Tab.3 Simulation results of reactive loss under rated load bias conditions

针对表3中的数据，利用MATLAB进行拟合，可得直流偏磁电流与无功损耗之间的关系如式(12)所示。

Q=2.28Idc+406.08

(12)

由表3与式(12)可以看出额定负载情况下，变压器直流偏磁下的无功损耗与直流偏磁电流之间同样呈线性关系，且直流偏磁电流相同的情况下，负载无功损耗明显大于空载无功损耗。

4.4 误差分析

文献[9]利用变压器磁-电路模型所得到的单台变压器空载情况下无功损耗与直流偏磁电流之间的比例系数K1为2.44；文献[11]所得比例系数K2为2.22。与本文计算所得比例系数K相比，其误差分析如下：

由式(13)、式(14)可知，与较为成熟的理论算法计算结果相比，其最大误差为5.33%。因此，计算结果可为治理1000kV特高电网直流偏磁无功波动提供相应的依据。

5 结论

(1)特高压变压器受直流偏磁电流侵扰后，其励磁电流会发生畸变，并伴随有高次谐波的出现，其中，随着直流偏磁电流的增大，基波、2次谐波、3次谐波的增加速度明显快于4次谐波、5次谐波等，即谐波次数越高，其幅值增长速度越慢。

(2)无论变压器空载运行或负载运行，其无功损耗与直流偏磁电流之间均呈线性关系，且比例系数大致相同，但直流偏磁电流相同时，负载无功损耗明显大于空载无功损耗。

(3)针对直流偏磁电流对变压器造成的危害，可通过在变压器中性点串联电阻、电容装置或反向直流电源来抑制直流偏磁电流的流通。据此，可以推测，如要从根本上治理直流偏磁电流对特高压变压器的影响，可从通过改变变压器自身的结构来抑制或消除直流偏磁电流对电力系统的影响。