快速掌握方法 巧妙解选择题

☉陕西省西安市西光中学 冯有涛

高考数学中，选择题几乎占据了数学试卷的近“半壁江山”，是拉开考生分数距离的一道屏障.如果能在选择题上快速正确破解，既达到尽量不丢分，又能节约时间，是我们解决选择题的目标所在.下面笔者结合高考真题，就快速破解选择题的比较常见技巧方法加以实例剖析.

一、直接法

直接法破解选择题是最常见的一种方法，其是直接从题设条件出发，运用数学的相关知识，通过推理和运算得出结论，进而作出相应的选择.直接法一般用来破解涉及概念、性质、定理、法则的辨析等问题.

例1（2017年全国卷Ⅲ理9）等差数列{an}的首项为1，公差不为0.若a2，a3，a6成等比数列，则{an}前6项的和为（ ）.

A.-24 B.-3 C.3 D.8

分析：设出等差数列{an}的公差为d，直接根据等比中项的性质建立关系式，结合等差数列的通项公式求解公差d的值，再利用等差数列的前n项和公式求解即可.

解：设等差数列{an}的公差为d.

因为a2，a3，a6成等比数列，根据等比数列的性质有a2a6=a32，即（a1+d）（a1+5d）=（a1+2d）2.

又a1=1，所以d2+2d=0，又d≠0，解得d=-2，

点评：直接巧妙利用等差（等比）数列的相应性质来解题，方法简单，思路快捷，可以省去一些不必要的计算.利用直接法解答选择题时，要尽可能地优化思路，力争小题不大做.

二、特例法

特例法是解决选择题时一种非常有效的特殊方法，其主要是结合题目条件，通过特殊值（或特殊图形、特殊位置、特殊模型）代替题设中的普遍条件，得出特殊结论，再通过适当的检测来作出判断.在涉及一些确定性的结论问题中，常采用特殊数值、特殊数列、特殊函数、特殊图形、特殊角、特殊位置等来特殊处理.使用特例法往往能简缩思维过程，降低答题难度，从而迅速得解.

例2 （2017年山东卷理7）若a＞b＞0，且ab=1，则下列不等式成立的是（ ）.

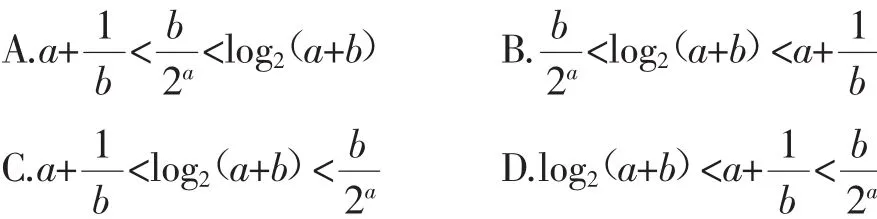
分析：涉及不等式的成立问题，可以利用条件中特殊值的选取，加以合适的验证，从特殊到一般，进而确定相应的关系式的大小问题.

点评：通过特殊值的选取可以比较方便快捷地处理此类问题，当然也可以根据对数函数的单调性来进行直接分析与判断.在解决函数中的大小比较问题时，往往优先考虑特值法、排除法等，操作比较简单，且容易判断.通过特殊值的选取来解决往往比采用相关知识的概念、定理、性质、公式等来处理更显得简单易操作.

三、筛选法

筛选法是根据题设条件入手，运用概念、性质、定理、法则或公式等的推演，逐步剔除干扰项，从而得出正确的判断.此类方法一般比较适合用于定性型或不易直接求解的选择题.

A.f（x）的一个周期为-2π

分析：根据三角函数的解析式，通过最小正周期、三角函数值的求解以及三角函数的单调性等来筛选与确定对应的结论的真假.

故选D.

点评：本题采用代入分析法，从选择支入手，结合三角函数的图像与性质，结合题设条件不断筛选不满足条件的选项，最后确定正确的选项，得到正确的答案.

四、图像法

在解答有关选择题的过程中，经常可以根据已知条件作出对应的曲线或有关图形或草图，借助几何图形的直观性来作出正确的判断，得出结论.由于选择题不要求写出解题的过程，使得图像法可以巧妙解题，提高解题的效率.

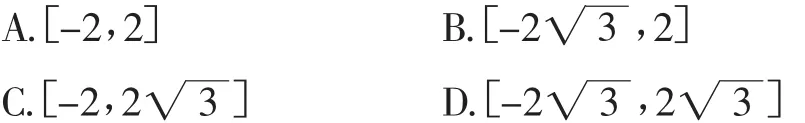
图1

综上分析可得-2≤a≤2，故选A.

点评：解决此类问题的关键是抓住函数的图像与性质，运用数形结合的思想和函数与方程的思想解答问题.特别地，涉及方程、不等式等问题，经常可以采用转化法，利用函数来处理，结合方程与函数的对应关系作出相应的图像，数形结合达到求解的目的.而涉及线性规划问题，也多采用数形结合思维，利用图像法来处理.

五、极限法

极限思维是一种重要的数学思想，灵活地借助极限思想，结合取极端值、极端点、极端位置等，避开抽象、复杂的运算，简单解题过程，优化解题效益，起到事半功倍的效果.

例5 （2015年浙江卷理8）如图2，已知△ABC，D是AB的中点，沿直线CD将△ACD折成△A′CD，所成二面角A′-CD-B的平面角为α，则（ ）.

A.∠A′DB≤α B.∠A′DB≥α C.∠A′CB≤α D.∠A′CB≥α

分析：直接通过题目条件判断相应两角之间的大小关系难度比较大，而通过极限法，结合翻折角的变化带动点的变化来分析，可以很快确定答案.

解：取极限思维：当沿直线CD翻折→180°，此时α→0°，排除选项A、C；

当沿直线CD翻折→0°，此时α→180°，排除选项D.故选B.

点评：本题采用极限法，从翻折的特殊位置入手，根据特殊位置对应的角来排除与应用，解答简单快捷.

解答选择题要真正做到“小题小做”，应该充分挖掘不同题目的“个性”，寻求最适合的方法，快捷地作出正确的判断，提高解题速度，为后续解题节省时间.H

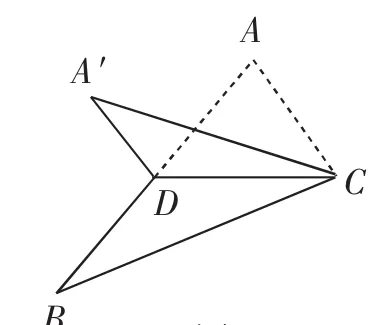
图2