数形结合，有效转化——以2018年江苏卷第12题为例

☉浙江省杭州第二中学钱江学校 杨冬梅

☉浙江省杭州高级中学钱江校区 邓 成

2018年的江苏卷整体难度不大，试卷设计平稳，比有些模考试卷更基础，整张试卷中基础题送分很到位，考生只要正确地掌握相关公式与定理，准确地计算即可得分，试卷中的中档题，有许多涉及的是经典题型、经典方法，多为历年高考的热点，如果考生在平时复习的时候多注重这类典型问题，多注重历年的常考知识点，掌握此类问题的通性通法，对付试卷中的中档题也是易如反掌.试卷中某些问题，如果考生选择恰当的解题方法还可以极大地提高运算的速度与准确性.本文以江苏卷第12题为例，谈谈此题的解题策略，与读者共勉.

一、身临其境，再见真题

题目 （2018年江苏卷第12题）在平面直角坐标系xOy中，A为直线l：y=2x上在第一象限内的点，B（5，0），以AB为直径的圆C与直线l交于另一点D，若=0，则点A的横坐标为______.

分析：由于题目中没有给出符合题意的相关图形，所以考生首先要根据题意作出大致图形，结论中要求点A的横坐标，所以猜想解答过程中可能少不了坐标运算，纵观题目，应该是将题设条件中的=0进行相关转化，可以直接进行数量积的坐标运算，也可以转化成线段AB与CD的垂直关系，或者进一步转化成相关线段的长度关系来解决，解题思路一下子明朗起来.

二、条件转化，各显神通

题设条件中有提及“以AB为直径的圆C与直线l交于另一点D，且=0”，都与点D关联，而点B已知，点A又为已知直线l：y=2x上在第一象限内的点，故点D的求解是关键.

1.曲线交点法

解法1：作出大致图像，如图1所示，因为A为直线l：y=2x上在第一象限内的点，所以可设点A（x1，2x1），所以以AB为直径的圆C的圆心所以圆C的方程为

图1

因为点A在第一象限内，所以x1=3，故点A的横坐标为3.

点评：本解法为纯代数解法，解法中运算量较大，直接根据题意，求出直线l与圆C的交点D，再将条件A■→B·C■→D=0进行坐标化后运算，没有过多的技巧性的东西，但对考生的计算能力有过硬的要求.

既然想到了要求点D的坐标，上述解法又太过烦琐，计算量又大，那么能否换个角度求点D的坐标呢？不难发现，圆C是以AB为直径的，所以AD⊥BD，这样就可以求出点D了.

解法2：因为AB为圆C的直径，所以AD⊥BD.因为直线l：y=2x，所以，所以直线BD的表达式为.联立直线l：y=2x，有解得所以D（1，2）.再设点A（x1，2x1），所以=（5-x1，又因为=0，所以（5-x1，-2x1）·=0，整理得（x1+1）（x1-3）=0，即x1=-1或x1=3.因为点A在第一象限内，所以x1=3，故点A的横坐标为3.

解法3：因为AB为圆C的直径，所以AD⊥BD，因为直线l：y=2x，所以kAD=2，kBD=-.设点D（x2，2x2），所以kBD=，解得x2=1，所以D（1，2）.再设点A（x，2x），因为=0，所以AB⊥CD，而C为圆心，所以直线CD为线段AB的垂直平分线，所以AD=BD，即，解得x=-1或x=3.因为点A在第一象限内，所以x=3，故点A的横坐标为3.

点评：解法2与解法3都简化了D点坐标的求法，解法2中求的是直线l与直线BD的交点，解法3中利用“两直线垂直时斜率乘积为-1”的结论，都快速地求出了D点坐标，解法3中有效地将=0转化为线段AD与线段BD的相等关系，减少了计算量.

2.几何意义法

题设条件中，直线l与圆C相交，且直线l的表达式已知，C又是AB的中点，不妨考虑将点C到直线l的垂线段与其他线段关联起来，运用几何意义解决问题.

解法4：如图2所示，连接CD，过C点作CH⊥AD.

图2

因为A为直线l：y=2x上在第一象限内的点，所以可设点A（x1，2x1）.因为=0，所以AB⊥CD.因为AC=CD，CH⊥AD，所以CH=AC，根据点到直线的距离公式，即·，整理有（x1+1）（x1-3）=0，所以x1=-1或x1=3.因为点A在第一象限内，所以x=3，故点A的横坐标为3.

点评：解法4巧妙地利用线段之间的垂直关系，在直角三角形中，数形结合，找到等量关系CH=AC这一关键点，借助点到直线的距离公式、平面上两点之间的距离公式，直接解出了A点的横坐标.

3.三角函数法

观察到A为直线l与直线AB的交点，直线l的表达式已知，若能求出直线AB的解析式，问题就解决了，而直线AB上的点B（5，0）又是已知，故只要求直线AB的斜率.

图3

点评：从所求结论直接入手，求出直线AB的解析式，倾斜角θ的设出及两角和的正切公式的运用是本解法的出彩之处.

4.构造相似法

要求点A的横坐标，只要求出点A到y轴的距离即可，作出垂线段，构造相似三角形，求出点A到y轴的距离.

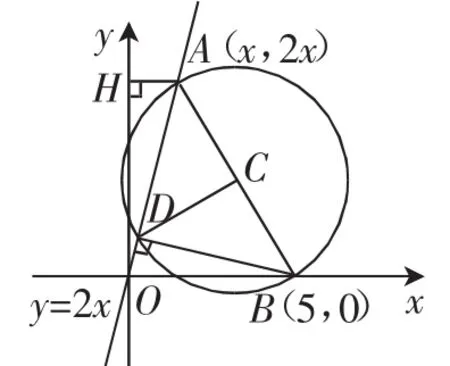
图4

解法6：如图4所示，过点A作AH⊥y轴，所以AH∥x轴，所以∠HAD=∠DOB，连接BD.因为AB为圆C的直径，所以AD⊥BD，所以∠AHO=∠ODB=90°，所以△AHO∽△ODB，所以.因为A为直线l：y=2x上在第一象限内的点，所以可设点A（x，2x），所以0，所以AB⊥CD.而C为圆心，所以CD直线为线段AB的垂直平分线，所以AD=BD，所以AO=AD+DO=BD+OD=，即x=3，故点A的横坐标为3.

点评：运用初中的数学知识，构造相似三角形，利用相似三角形的相似比的性质来解答，没有高中数学中高大上的感觉，但过程显得通俗、易懂.

三、解后小结，能力升华

本题属中档题，主要考查平面向量数量积、直线与圆的位置关系等，对考生而言，准确理解题意，并正确画出符合题意的图形非常关键，只要能准确理解题设条件“A■→B·C■→D=0”，并实施有效的转化，本题还是易解的，在本文中，我们从不同的角度、不同的层面对题设条件进行相关转化，发现此题解答方法如此众多，但是要考生在规定时间内，能够运用最合适的解题方法快速地解决问题，这对考生的个人数学能力有较高的要求，另外，这些解法主要体现了数学中常用的两大数学思想：数形结合的思想、转化与化归的思想.W