叠波模型视角下学生概率比较策略发展的再审视
2018-10-16何声清
何声清
(北京师范大学教育学部 100875)
1 引言
无论是课程目标的阶段划分,还是教材内容的螺旋编排,亦或是教学过程的路径设计,这些工作的开展都应以尊重学生的认知发展规律为前提.传统的认知发展理论大都属于某种阶梯模式(staircase model)或等级模式(hierarchical model),其关注点多聚焦于认知发展的阶段性(如认知发展阶段理论[1])或认知水平的层次性(如SOLO分类理论[2]).
数学问题的美常常体现在答案的确定性和方法的多样性.同一个作答反应可能源自不同的解决策略,这些策略甚至有优劣、正误或多种层次之分.例如,新近一项有关学生概率比较策略的研究表明[3]:对于问题“不透明的盒子里有白球、黑球各2个,它们除颜色外都相同.从盒子里随机摸出2个球,摸出‘一个是黑球而另一个是白球’和‘两个都是白球’这两种情况哪个可能性更大”,初中生的作答正确率为37.75%,而正确策略的使用频率则仅为14.73%.这说明,在能够作出正确判断的学生群体中,有相当一部分学生使用了不当的策略.
可见,仅仅从学生的最终答案来判断其认知水平在科学性上尚存在局限和偏颇,我们还应该深入考察学生问题解决的策略表现及水平差异,分析学生持有不当策略的潜在原因并探索可行的干预手段,厘清学生策略发展的过程并据此揭示其中的规律.前研究厘清了学生概率比较的典型策略并考察了其发展趋势,但比较遗憾的是,该研究尚未就“学生策略发展的竞争、替代机制”等问题做更深入的探索,亦没有从这个角度对“概率比较”问题解决的教学提出更多建议.本文在前研究的基础上,从理论层面重新审视学生概率比较策略的发展机制并据此探讨其一般模型以及提出相应的教学建议.
2 问题解决策略发展的叠波模型
当代著名心理学家Siegler早在上世纪90年代就提出了策略发展叠波理论(overlapping waves theory).该理论认为,儿童在其认知发展的不同阶段对于特定问题的解决一般都持有不同的策略,并且这些策略常常有对错、优劣和繁简之分.学生问题解决的策略通常表现出情境适应性和时间适应性.情境适应性是指学生会在不同的问题情境中倾向于诉诸不同的策略.时间适应性是指学生在不同的认知发展阶段运用不同策略的频率在不断变化,能够越来越多地使用“好”的策略[4].
策略的“发展”主要体现在4个方面:接受新的策略;增加新策略的使用频率;策略使用有效性的提高;越来越擅长使用最佳策略.不同年龄段学生都有其特定的“主打”策略和“替补”策略;随着年级/年龄的递增,各种策略的使用频率呈现“此消彼长”的动态发展;在此过程中,新的策略被发现和运用,陈旧的策略被永久遗弃;策略运用的有效性、贴适性也随年龄/年级的递增而提升,学生的认知发展在策略优化过程中得以实现.
该理论与以往认知发展阶段理论的最大区别是:它更多地关注到策略发展的渐进机制,认为儿童的认知发展是“渐进的”而非“突变的”,尽管新的策略不断被采纳,但这并不意味着旧的策略被随即终止,策略的发展是在相当长的一段时间里新、旧策略的持续竞争中得以实现的.
3 叠波模型视角下学生概率比较策略的发展机制
在前一项研究中,研究者设计了5个有关概率比较的测试题目[3],并从学生的判断结果和理由解释两个方面收集了学生的作答数据,本文的分析正是基于该套测试题目和相应的数据库而进一步展开的,受测被试也与上述研究一致.5个测试题目详见表1.

表1 测试题目的结构
前研究还区分了学生概率比较的7种典型策略(表2),并以年级为变量考察了学生各种策略使用频率的发展状况[3]:随着年级的递增,学生正确策略的使用频率总体上呈现上升趋势,部分朴素策略的使用频率总体上呈现下降趋势,而尚有部分朴素策略的使用频率长期居高不下.
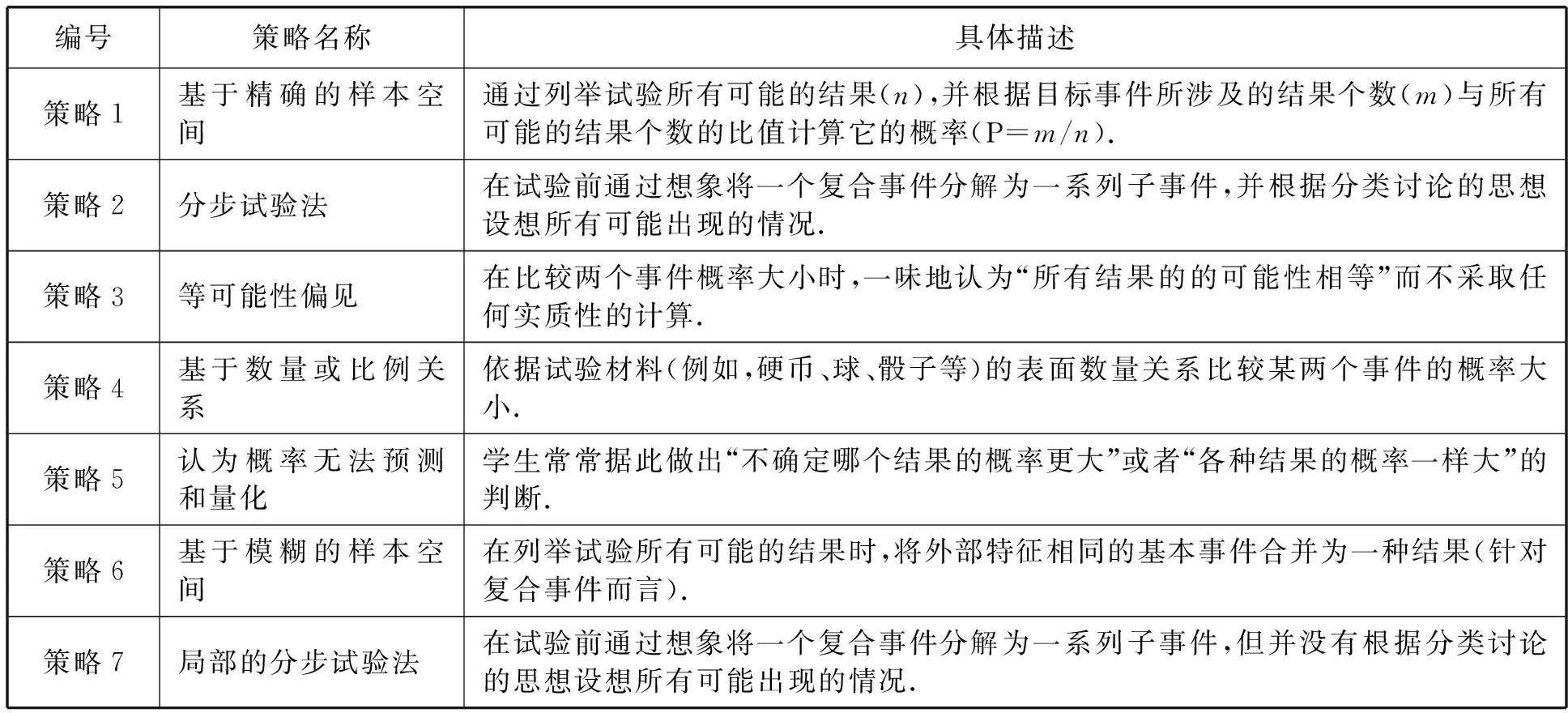
表2 学生概率比较的典型策略
然而进一步的问题是:各个年级组间正确策略的使用频率是否存在显著性差异?随着年级的递增,学生概率比较策略是以怎样的机制进行竞争和替代的?上述策略发展机制的潜在原因是什么?教学如何适应学生的策略发展规律?本文以叠波模型为视角对上述问题进行分析,以期从理论层面进一步厘清学生概率比较策略的发展机制.
3.1 时间适应性:不同年级学生策略使用的倾向性及其差异
对不同年级学生策略使用的频率进行了统计,这部分数据已在前一项研究中进行了初步报告和解读[3],不再赘述.进一步发现,学生概率比较策略发展的数据符合叠波模型的理论预期,如图1所示.若从叠波模型的视角重新审视前文数据,可以发现:策略的使用随着年级的递增呈现此消彼长的动态发展趋势,有的策略逐渐在竞争中被替代,有的策略则逐渐成为主导.具体而言:七年级学生的“主打”策略基本是朴素策略,正确策略使用频率不高;八年级学生策略的使用频率相对均衡,发展呈现多样化;九年级学生的优势策略发展强劲并开始成为主导,部分朴素策略的使用频率趋于缓和.
以上发展特点也进一步表明:学生概率比较策略的发展是一个“渐进的”而并非“突变的”过程,即优势策略的发展不是一蹴而就的,即便九年级学生所使用的策略也并非全然达到了最优水平,他们同样持有一些顽固的、难以消除的朴素策略.
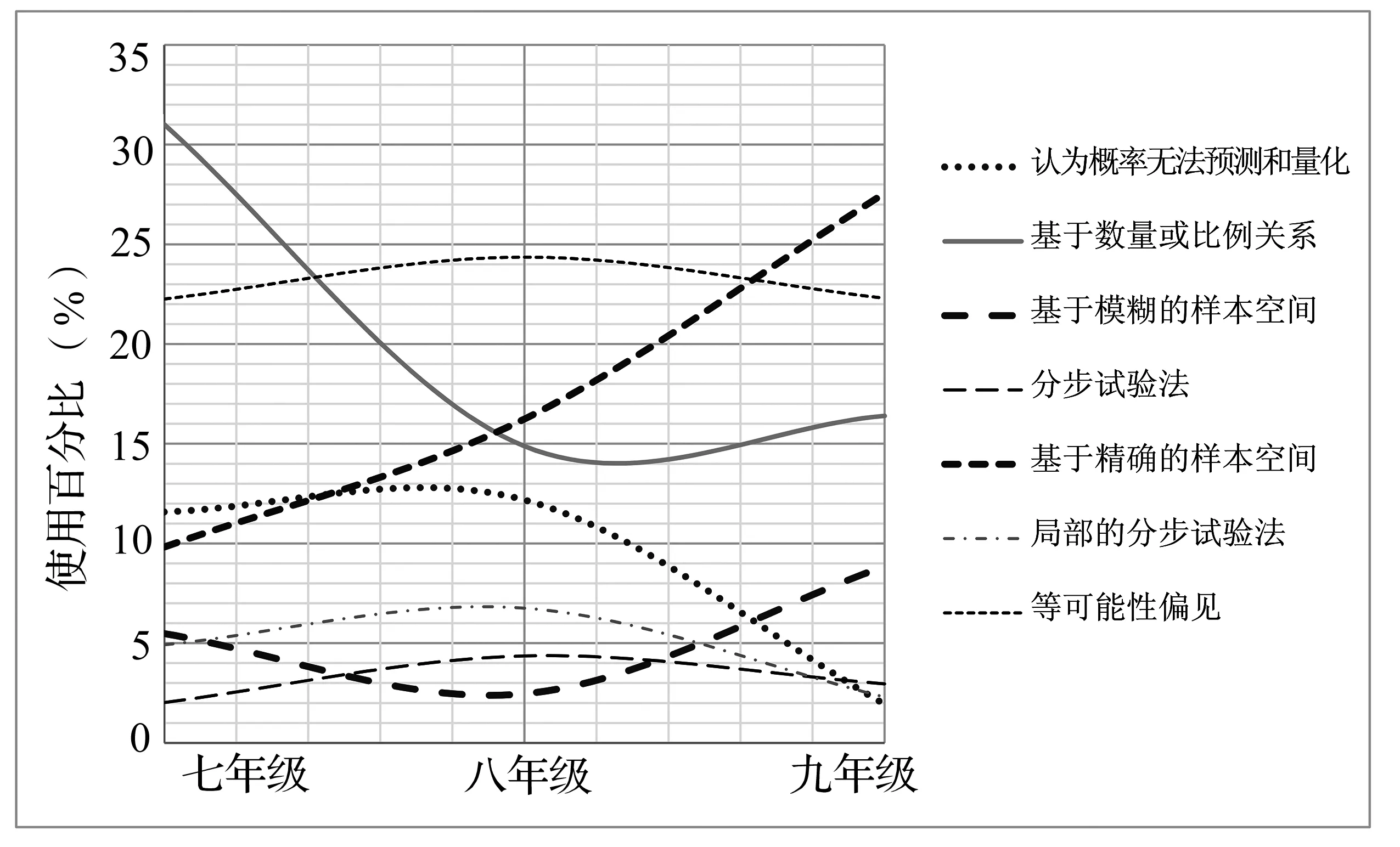
图1 七~九年级学生“概率比较”策略发展的叠波模型
对各个年级组间正确策略(包括“基于正确的样本空间”和“分步试验法”)的使用频率进行差异检验.结果表明,除了Q2(χ2=4.646,p=0.098)以外,七~九年级学生在其余各个测试题目上正确策略的使用频率均存在显著性差异(Q1:χ2=6.383,p<0.05;Q3:χ2=8.578,p<0.05;Q4:χ2=13.133,p<0.01;Q5:χ2=6.383,p<0.05).这进一步表明,除了个别测试题目以外,学生在大多数题目中优势策略的发展均是显著的.那么,学生为何在Q2的问题解决中优势策略的发展不显著呢?这可能与该测试题目本身的难度及学生的认知局限有关:该题目涉及的黑球和白球均是2个,摸出的2个球所有可能的结果有6种(基本事件),其中“1个黑球和1个白球”这种情况包含了“黑1白1”、“黑1白2”、“黑2白1”及“黑2白2”4种组合.然而,学生在对所有可能结果进行组合的过程中遇到了困难,他们难于厘清“1个黑球和1个白球”的4种可能的组合,有84.8%的学生认为所有可能结果为“2个白球,2个黑球,1黑1白”,有7.8%的学生认为所有可能的结果为“2个白球,2个黑球,1黑1白,1白1黑”[5].在概率比较时,有11.8%的学生正是基于他们对样本空间的上述错误理解而进行的判断,有26.5%的学生则是源于其持有的“等可能性偏见”而进行的判断,另有23.5%的学生从表面的数量关系出发,认为“黑球和白球均是2个,所以两种情况的概率一样大”.可见,各年级学生均在该问题的概率比较任务中遇到了困难,这一方面源于他们的组合知识缺乏(尽管人教版教材在九年级上册涉及到“用列举法求概率”,但本测试进行时他们尚未学习到该章节),一方面源于他们不良概率直觉的根深蒂固.
3.2 情境适应性:不同问题情境下策略使用的倾向性及其差异
就学生在不同测试题目中策略的使用频率进行统计及差异检验(表3),结果表明:
(1)学生在Q1中的主导策略是“等可能性偏见”(33.3%)和“基于精确的样本空间”(20.6%).尽管该测试题目涉及的球个数最少,但却给学生造成了不小的干扰.有20.6%的学生能够通过构造样本空间来进行概率比较,这不足为奇,甚至这个百分比还可以更高,因为它一共仅有3种可能的结果.但是更多学生的作答却表现出了“等可能性偏见”,且该策略的使用频率在5个测试题目中处于最高水平.
(2)学生在Q2中的主导策略是“等可能性偏见”(26.5%)和“基于数量或比例关系”(23.5%).“等可能性偏见”依然被学生频繁地使用,这与该测试题目的自身特点有关:它涉及的两种颜色球均是2个,而这种高度对等的外表特征很容易诱导学生作出“因为两种球个数相等,所以各种情况的可能性相同”的判断.相对于Q1而言,学生使用“基于精确的样本空间”策略的频率有所降低,而“基于数量或比例关系”的频率则相对提高.这仍然与上述高度对等的外表特征有关,其次还与学生组合知识的局限有关,他们容易被“1个黑球和1个白球”所涉及的4种基本事件所混淆.事实上,学生在该题目中“基于模糊的样本空间”策略的使用频率确实达到了5个题目的最高水平(11.8%),这说明学生在列举所有可能的结果时倾向于将基本事件中相同的样本混淆为一种情况.
(3)学生在Q3中的主导策略是“等可能性偏见”(19.1%),另外“基于精确的样本空间”和“基于数量或比例关系”策略的使用频率相当(均为16.2%).
(4)学生在Q4中的主导策略是“等可能性偏见”(25%)、“基于精确的样本空间”(22.5%)及“基于数量或比例关系”(21.1%).学生在该测试题目中的策略使用出现了高度的竞争关系和两极分化:一方面,“等可能性偏见”和“基于精确的样本空间”的使用频率依然居高不下,其原因可能与Q2类似——高度对等的外表特征给学生的上述直觉性策略提供了土壤.另一方面,“基于精确的样本空间”策略的使用频率处于5个题目的最高水平,甚至高于Q1.究其原因,题目要求学生“分别”从盒子里个摸出一个球,这在一定程度上提示了学生对左右两个盒子里摸出的球进行组合.
(5)学生在Q5中的主导策略是“基于数量或比例关系”(29.4%),而其他策略的使用频率则均相对不高,其中“等可能性偏见”的使用频率更处于5个题目的最低水平.这也容易理解:该题涉及的白球个数明显多于其他颜色的球,这大大降低了题目的干扰性,并提高了“基于数量或比例关系”策略的有效性.此外,“分步试验法”的使用频率在该题达到最高水平,这与题目情境有关:“分别”从两个盒子里各摸出1个球对学生的分步策略起到了一定的暗示作用.然而问题是,学生在Q4中使用该策略的频率则很低,这正是因为其高度对称的外表特征诱导了“等可能性偏见”和“基于数量或比例关系”策略,而这些策略在与“分步试验法”的竞争中被采纳.
(6)不同策略的使用频率发展情况也与题目的情境有关.例如,不同年级学生在“基于精确的样本空间”策略的使用频率上的发展一般都达到显著,但是在Q2中却并非如此,这再一次证实了学生在该题中的策略运用存在局限,正确策略的使用也容易在竞争中被朴素策略所替代.再例如,不同年级学生“等可能性偏见”的发展未达显著,其使用频率一值居高不下,这说明它十分顽固、难以消除.
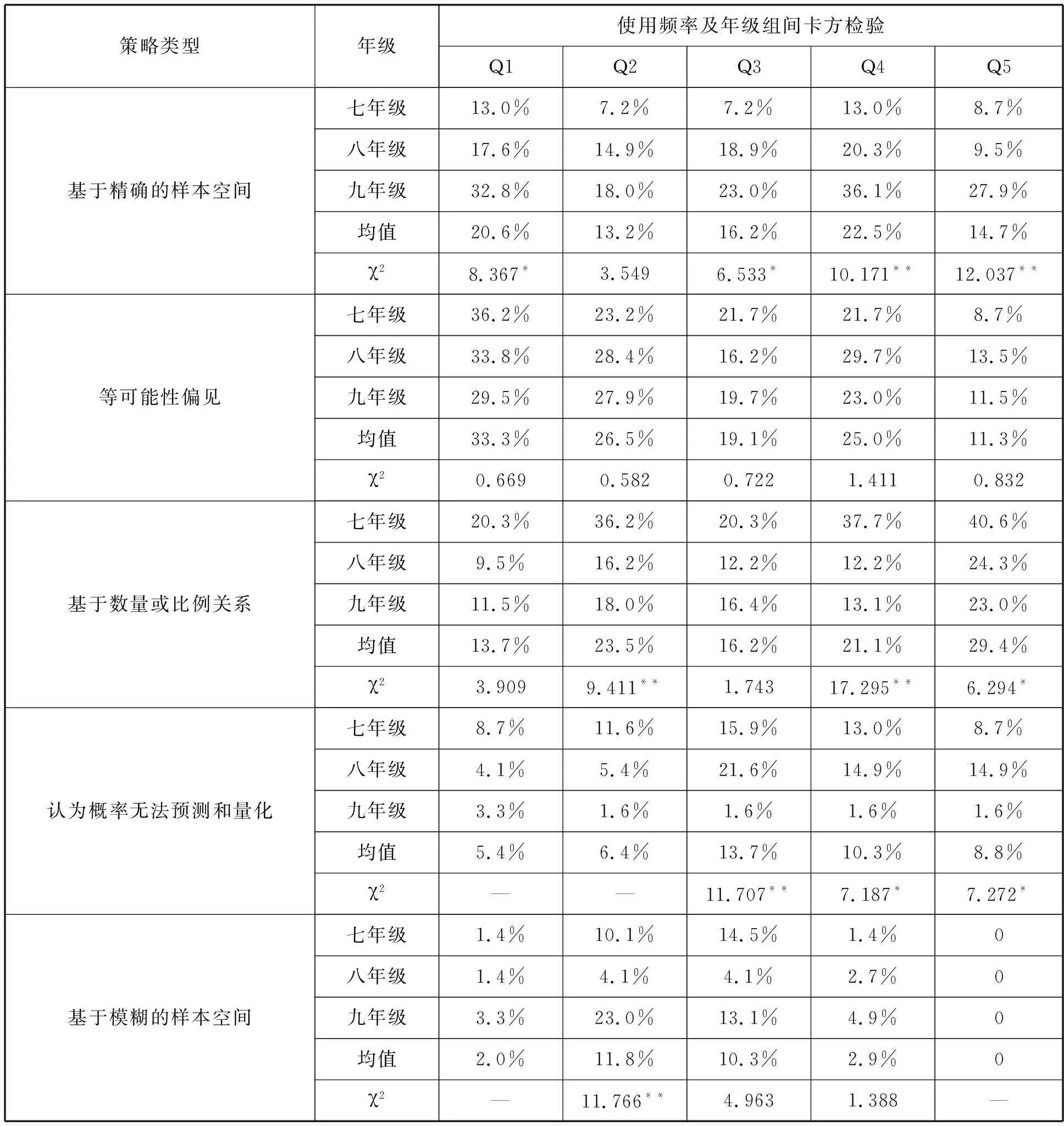
表3 学生在不同测试题目中策略的使用频率及卡方检验
注:*表示p<0.05,**表示p<0.01;考虑到部分年级在个别策略(“分步试验法”和“局部的分步试验法”)上的使用人数期望次数小于5,这不满足卡方检验的前提,故没有对这些策略的使用频率进行卡方检验.
3.3 不同策略间竞争和替代的一般规律和基本机制
基于上述讨论可以发现,学生概率比较的策略一般是按照“个别主导→相互制衡→个别主导”、“策略贫乏→策略丰富→策略优化”的方向发展的.具体而言,可以归纳出如下的一般规律和基本机制:
(1)从“不可知论”到“可知论”.古典概率的一个鲜明特点是理论先验性,即在试验前能够对事件的概率进行理论推演,通过将目标事件所包含结果的个数与所有可能的结果个数作比而计算出来.换言之,尽管最终会出现哪种结果不得而知,但可以事先在理论上对其进行预判.而学生往往持一种“不可知论”的观点,认为“事情没有发生,不能知晓哪种结果更可能发生”、“只有上帝才知道会出现什么”,等等.数据表明,九年级学生较七、八年级学生在“认为概率无法预测和量化”的使用频率上有了明显的降低,而在“基于精确的样本空间”策略的使用频率上则达到了峰值.值得提及的是,尽管“基于模糊的样本空间”尚不属于正确的策略,但它至少反映了学生能够从样本空间的角度出发进行概率比较(这也是“可知论”的一种体现),而七~九年级学生关于该策略的使用频率基本是呈现上升发展的.
(2)从“数量关系”的表象到“样本空间”的实质.如前所述,古典概率计算的基本依据是“目标事件的结果个数÷所有可能的结果个数”.如果将本研究中的题设改为“摸出1个球”,那么从不同颜色球的数量或比例的角度去分析是基本合理的.然而对于复合事件的概率计算而言,其可能的结果(基本事件)是一个组合的形式,上述的有关“数量或比例关系”的解释在这种情况下就显得苍白无力.数据表明,八、九年级学生较七年级学生在“基于数量或比例关系”的使用频率上有了明显的降低.与此同时,“基于精确的样本空间”策略的使用频率则明显提高,“基于模糊的样本空间”策略的使用频率也基本上呈现上升趋势.
(3)从朴素的组合推理到精确的组合推理.从“不可知论”到“可知论”的发展是学生概率思维发展的第一步,从“基于数量关系”到“基于样本空间”则体现了更深层次的发展.但是就样本空间的认识而言,学生的发展也并非一蹴而就的——它与学生组合知识的发展有关.数据表明,八年级学生“基于模糊的样本空间”策略的使用频率处于三个年级的最低水平,九年级学生该策略的使用频率反而较该年级有明显的提高.但总体而言,“基于精确的样本空间”策略的使用频率是逐级提高的,且发展速度高于“基于模糊的样本空间”.需要指出的是,学生的“等可能性偏见”在很大程度上源于其对样本空间的模糊认识:以Q2为例,当认为所有可能的结果为“2个白球,2个黑球,1黑1白”这3种情况时,他们则倾向于认为“3种结果的可能性相等”.但数据表明,学生“等可能性偏见”的频率一直居高不下且处于一个较高的水平,这也反映了学生组合推理发展的困难性和局限性.换言之,从“朴素的组合推理”到“精确的组合推理”是学生概率比较策略发展的一个大势,但这个发展过程是曲折和缓慢的.
4 对概率教学的启示
4.1 尊重策略使用的局限性和朴素性,关注错误策略的消除
学生的策略发展与其知识发展、思维水平、生活经验等多重因素有关,他们早期使用的策略不可避免地存在一定的局限性和朴素性.研究表明,即便成人也难免表现出对概率的错误直觉和认识[6].因此,我们应充分尊重学生的认知局限性,在策略的运用上不可有过高的要求.尽管如此,我们还应致力于通过教学系统地干预并纠正他们的错误策略.研究表明,尽管策略的发展是“渐进”的,但教学干预能够帮助他们更快摆脱错误认识而产生“突变”的效果[7].
4.2 把握策略发展的渐进性和竞争性,着力优势策略的培养
如前所述,策略的发展是一个竞争、替代并逐渐适应的渐进过程,最终的结果是优势策略的建立与巩固.本文中“基于精确的样本空间”策略是一种优势策略,尽管它的使用频率基本是持续上升的,但在此过程中也不可避免地面临着来自其他策略的竞争,因而其发展的过程是渐进的.例如,七年级时主导策略是“基于数量或比例关系”,八年级时的主导策略是“等可能性偏见”,“基于精确的样本空间”与“基于数量或比例关系”策略的使用频率基本平分秋色,九年级时“基于精确的样本空间”策略的使用频率才发展到顶峰.另外,“基于精确的样本空间”策略的发展还受到学生组合知识的影响,后者的局限不仅限制了其对样本空间的理解,还是诱导“等可能性偏见”的原因之一.因此,教学应正视学生优势策略发展的曲折性和渐进性,着力加强学生对组合知识、样本空间等概念的理解,让学生优势策略的发展更加顺利和稳定.
