基于HPM的《三角学序言课》教学设计*
2018-10-16张海强
张海强
(江苏省宜兴中学 214200)
2.本文是江苏省教育科学规划“十二五”立项课题《MKT视角下的高中数学课堂教学设计研究》(编号:D/2015/02/363,主持:张海强、刘国祥)的研究成果之一.
1 引言
2017年10月26日,由华东师范大学教师教育学院、宜兴市教师发展中心、宜兴市张海强高中数学名师工作室联合举办大型公开教学活动,笔者开设《三角学序言课》,学生来自于江苏省宜兴中学高一精一班,知识面广,反应敏捷.本课是三角学序言课,内容包括三角函数的图象与性质、三角恒等变换和解三角形,等.
2 序言课和HPM
2.1 关于序言课
序言课的教学是为了促进新知识的学习,具有先行组织者的作用.序言课的设计追求大立意、高境界,旨在勾勒特定内容的研究蓝图,引发学生的思考,激发学生的学习兴趣.因此,序言课的设计宜重“虚”而不重“实”,重“廓”而不重“具”.
序言课的设计不宜设定一个通用的模式,应视具体内容而定.但序言课应按一定的线索来设计,如知识发展的线索、研究思想的线索、重要人物的线索、知识应用的线索等.序言课大致可分为三类:知识层面的序言课、方法层面的序言课和文化层面的序言课.
序言课要注重回答以下几个问题:(1)为什么要学习这个内容?它的学习价值是什么?(包括人文的、思想的、逻辑的等方面)(2)这个内容是什么?(包括它的历史变迁、发展过程、研究思想和方法等方面)(3)如何学好这个内容?(主要是学法指导)
2.2 关于HPM
HPM是History&Pedagogy of Mathematics的简称,即数学史与数学教育.在过去的四十余年间,HPM领域的研究工作涉及五个方面:
·关于“为何”和“如何”的探讨;
·教育取向的数学史研究;
·数学理解的历史相似性实证研究;
·数学史融入数学教学的实践;
·HPM与数学教师专业发展.
其中数学史融入数学教学实践的方式主要有三种:一是提供直接的历史信息;二是借鉴历史进行教学;三是开发对数学及其生活文化背景的深刻觉悟.其中第二种方式就是发生教学法,即通常所说的HPM视角下数学教学的主要内容.
本教学设计定位于文化层面的序言课,它将从HPM的视角,以时间为轴线,选择三角学发展过程中的重大事件和关键人物为节点,用故事的形式展示三角学发展的历史画卷,以高度凝练的语言揭示三角学研究的目的、内容和方法.
3 基于HPM的序言课案例设计
案例1引言
出示两件文物:一件是大英博物馆永久馆藏——莱因德纸草书(古埃及),其中第56-60题均与金字塔的计算有关;另一件是哥伦比亚大学珍藏的“普林顿322”号泥版(古巴比伦),其中涉及大量的勾股数,它表明巴比伦人比毕达哥拉斯早一千年知晓了毕达哥拉斯定理.
设计理由:三角学起源于古埃及和古巴比伦,选择两件重要且具有代表性的文物作为本节课的引言,引出课题:三角学的缘起、内容与方法.
案例2词源考证
三角学的英文单词trigonometry,来源于希腊文字trigonon和metron,前者相当于英文单词triangle,意思为三角形,后者相当于英文单词measure,意思为度量、测量.
早期的三角学是天文学的一部分,天文学家只是关注“量天的学问”,不关注“量地的学问”,因此,早期三角学的内容主要是球面三角学.
设计理由:从三角学的词源考证入手揭示了早期三角学的内容,从三角学与天文学的关系阐释了早期三角学的工具性.
案例3正弦函数的演进
在“量天”的计算过程中有一个核心技术,即在圆中,求已知弧长所对弦的长度.这涉及正弦函数的定义.希腊数学家希帕普斯(Hipparchus)认为正弦是圆弧所对弦的弦长;印度数学家阿耶波多(Aryabhata)认为正弦是圆弧所对弦的半弦长;奥地利数学家雷蒂库斯(Rheticus)认为正弦是比值,他最先给出角的正弦概念,把原来弧的正弦改成了锐角的正弦.
设计意图:正弦函数概念的变迁反映了三角函数的历史发展.“正弦是比值”这一定义与学生初中学习的正弦函数定义相吻合,与学生的已有知识挂钩,在学生的心里产生强烈的共鸣.
案例4弦表的编制
在缺乏现代计算工具的古代,如何才能快速求出已知弧所对弦的弦长呢?
古人采用编制弦表的方式来达到快速计算的目的.
(1)托勒密(Ptolemy)
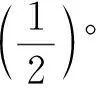
那么他是如何做到的呢?其中重要的工具之一就是著名的Ptolemy定理:圆内接凸四边形ABCD中,AC·BD=AB·CD+AD·BC.
问题1:在图1中,你能利用托勒密定理得出哪些三角公式?
(注:可以得出sin2α+cos2α=1;
sin(α+β)=sinαcosβ+cosαsinβ;
cos(α+β)=cosαcosβ-sinαsinβ.)
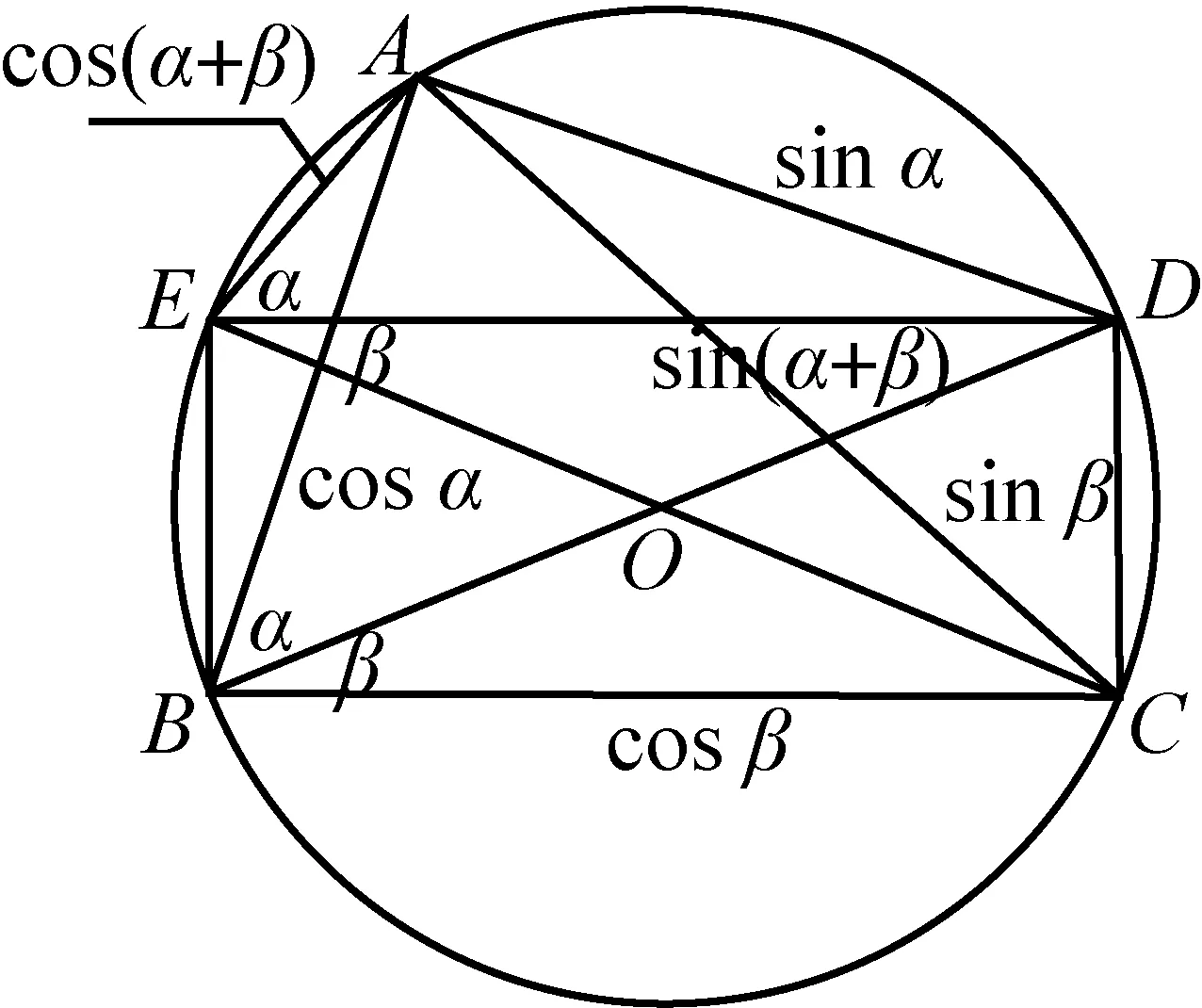
图1
(2)僧一行
一行,本名张遂,中国唐代著名的天文学家和佛学家.他主张在实测的基础上编订历法,编制了《大衍历》.设计制造了“水运浑天仪”,提供了相当精确的地球子午线一度弧的长度.
他在《大衍历》“步晷漏术”中建立了从0°到80°的每度影长与太阳天顶距之间的对应数表,其本质即为正切函数表,堪称数学史上最早的正切函数表.
(3)阿布•韦发
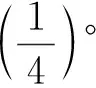
阿布•韦发是三角学历史上最早使用所有六个三角函数、并系统研究它们之间关系的数学家.
问题2:在图2中,你能发现哪些三角函数关系?
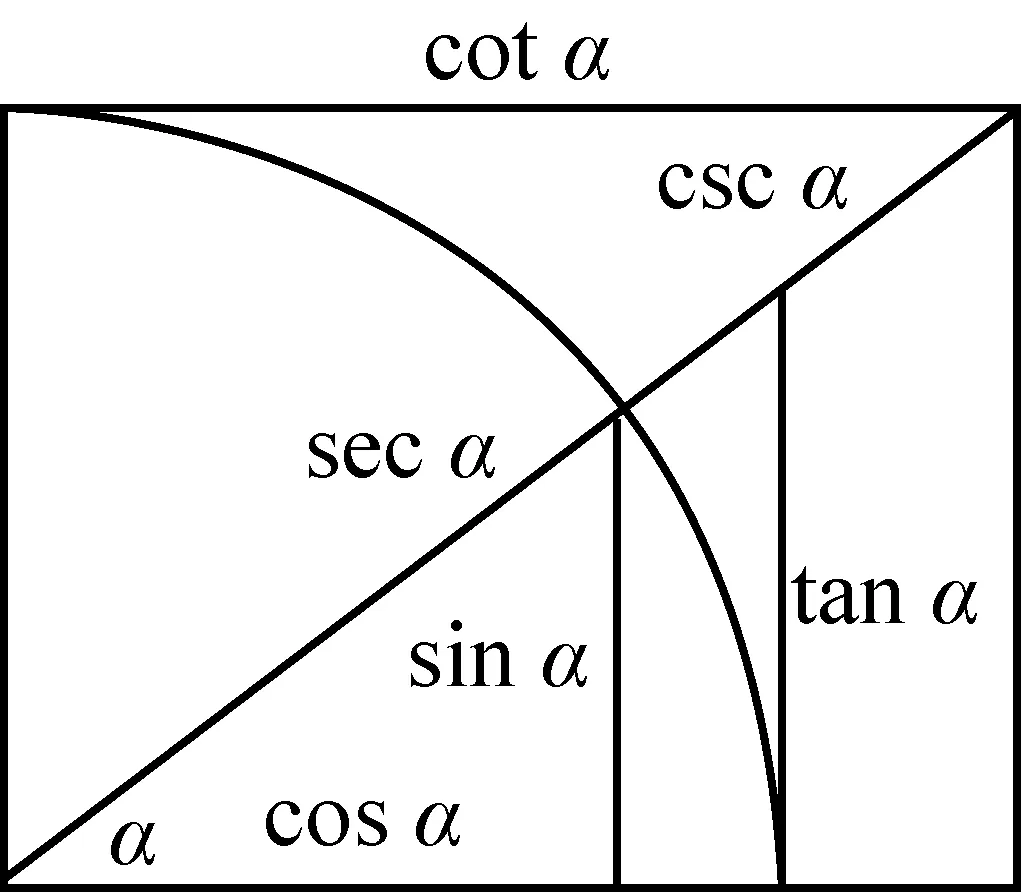
图2
(注:tanα:1=sinα:cosα;cotα:1=cosα:sinα;
tanα:1=1:cotα;sin2α+cos2α=1;
需要指出的是:阿布•韦发所生活的时代,三角函数并不是用比率,而是用线段来表示的,同角三角函数关系则往往以比例的形式出现.)
阿布•韦发为编制精确的弦表,几乎演绎出了所有的三角公式.但三角学仅局限于锐角,而且每个三角公式均脱胎于几何证明.这正是我们将要学习的“三角恒等变换”的主要内容.
设计理由:编制弦表是三角学作为计算工具的重要工作,在编制弦表的过程中演绎出了丰富的三角公式,这些公式仅局限于锐角,均脱胎于几何证明.这一教学环节有利于学生认识、理解和记忆三角公式,也为三角恒等变换的教学提供了全新的视角.
案例5承前启后的韦达
韦达是三角公式的集大成者,他总结了前人的三角学研究成果,并补充了自己发现的新公式,系统论述了平面三角与球面三角,采用完整的代数公式解决斜三角形和球面直角三角形问题,首次给出余弦定理的现代表达形式.这即是我们将要学习的“解三角形”的主要内容.
韦达被称为代数学之父,他承前启后,在数学符号语言方面有独到的表现.他首次将代数变换的方法引入三角学,为解析三角学的出场准备了必要的布景.
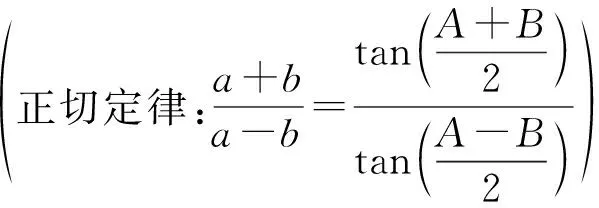
韦达还是第一个将代数方法系统应用到三角学中的数学家,韦达就像是一个守门人,他转变了三角学这道门,从此三角学不仅通向几何,而且通向代数.
韦达是初中学生熟悉的、为数不多的数学家之一,把韦达作为三角学的关键人物,可以使学生产生“他乡遇故知”的感觉!
案例6三角学的近现代发展
从日常生活的力学世界中选择四幅图片:弹簧振子、钟摆、大提琴、摩天轮.
问题3:你能从中发现什么内在联系?你准备用什么模型来刻画它?
(通过动画分别展示钟摆和摩天轮随时间运动的图象(正弦型图象))
于是欧拉来了!
在4000年的历史发展中,三角学的研究对象本质上是圆,欧拉首次用单位圆中的有向线段表示三角函数,故三角函数又称圆函数.
三角函数是匀速圆周运动的本质体现,研究圆周运动,最重要的是研究圆周上一点(x,y)与角θ的函数关系.欧拉使三角学成为一门独立的学科.
三角学从强调计算转变到强调函数方法,函数方法成为研究三角学最有力的工具,三角函数则是刻画“周期现象”最理想的数学模型.
值得一提的是,欧拉的著述浩瀚,不仅包含科学创见,而且富有科学思想,他给后人留下了极其丰富的科学遗产和为科学现身的精神.历史学家把欧拉同阿基米德、牛顿、高斯并列为数学史上的“四杰”.如今,在数学的许多分支中经常可以看到以他的名字命名的重要常数、公式和定理.
欧拉是所有中国数学家和中国人的导师.这首先是因为每一个进入学校接受教育的人,都要学习他所创造的数学知识;这更是因为,他那苦难而光辉的一生给后世无限的启迪,教导人们如何做人,如何做学问,如何生存.
设计理由:18世纪以后,三角函数与振动、波动现象的关系成为人们关注的焦点.突出三角函数与振动、波动的联系要抓住三角函数的本质.三角函数就是匀速圆周运动的本质表现,因此三角函数也称圆函数.这就确定了单位圆在三角函数研究中的工具地位.而研究圆周运动最重要的是研究圆周上一点(x,y)与角θ的函数关系,这就指出了三角函数研究的研究内容和研究方法.
引导学生发现日常生活中比比皆是的周期现象,并提出问题:如何用数学模型来刻画周期现象?让学生感悟三角函数是刻画“周期现象”的数学模型.
欧拉是三角学发展中的关键人物之一,对欧拉生平的介绍不仅具有教学价值,而且具有重要的教育功能,体现数学在“立德树人”教育中不可或缺的地位和作用.
案例6变迁与跃进
三角学起源于古埃及、古巴比伦,兴盛于古希腊,发展于印度、中国、阿拉伯,完善于欧洲地区.简言之,三角学经历了从弧到角、从全弦到半弦、从线段到比值、从球面三角学到平面三角学、从计算三角学到解析三角学、从天文计算方法到数学独立分支的演进过程,三角学发展史实际上也是一部浩瀚的人类发展史.
设计理由:以高度凝练的文字概括了三角学的历史发展过程,从数学史的角度描述了三角学的大致轮廓,体现了序言课重“虚”不重“实”,重“廓”不重“具”的特征.
4 结语
序言课有助于为学生今后的学习构建知识框架,以形成新知识的固着点,为学生学习新知识做好必要的知识准备和心理准备.数学史则为序言课的设计提供了独特的视角和丰富的资源;首先,数学史揭示了特定知识的缘起及其发展过程,这一过程正是人类对特定数学知识的认识过程;其次,数学史演绎了特定知识从古到今对推动时代发展和人类文明进步所作出的巨大贡献;再次,数学史中的轶事具有故事性和趣味性,可以引起学生的学习兴趣.因此,基于HPM的序言课可成为文化层面的序言课教学设计的一种重要操作样式.
