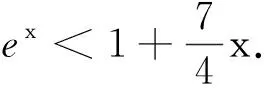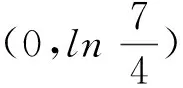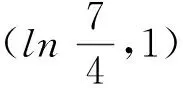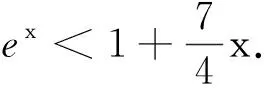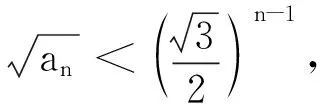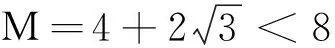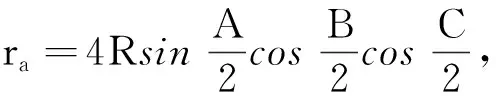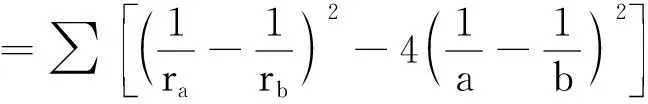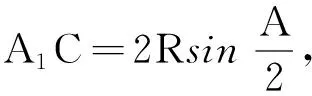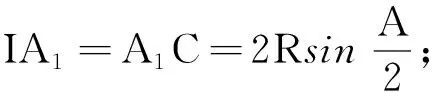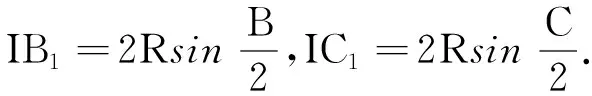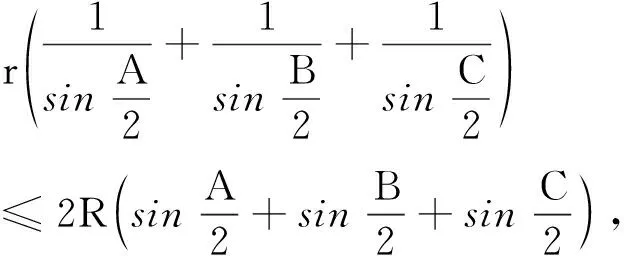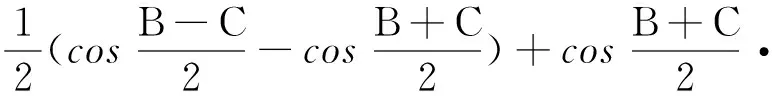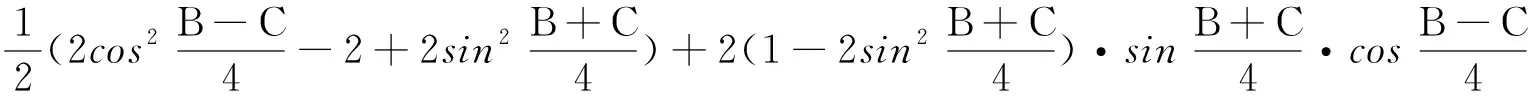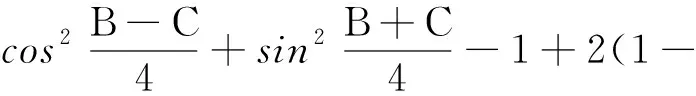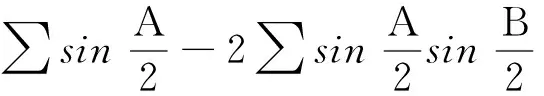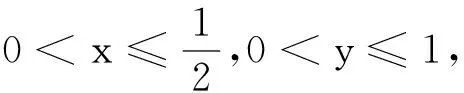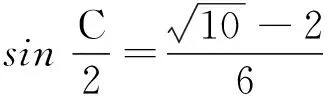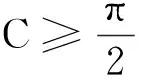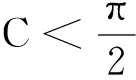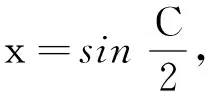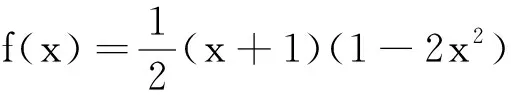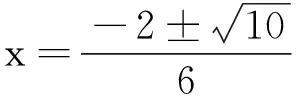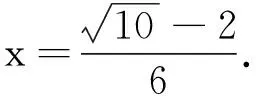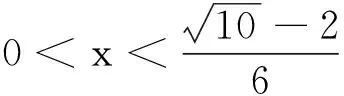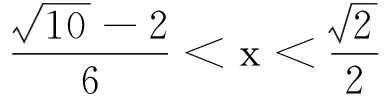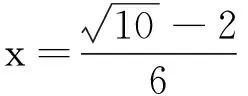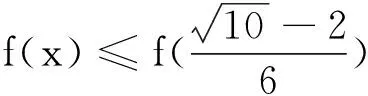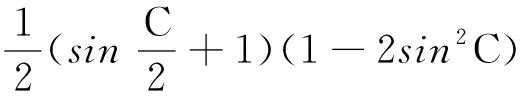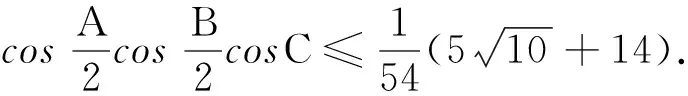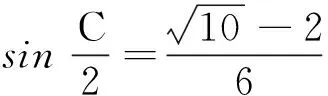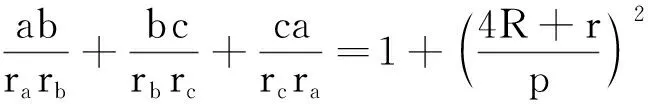数学问题解答
2018-10-16
2018年7月号问题解答
(解答由问题提供人给出)

(浙江省宁波市甬江职高 邵剑波 315016)
解先给出以下两个结论:
结论1: 当n≥2时,0 结论1的证明:用数学归纳法. (1)当n=2时,a2=ln(e-1), 故有0 (2)假设当n=k时结论1成立, 即0 那么当n=k+1时, ak+1-ak=ln(eak-ak)-lneak 故ak+1 由不等式ex>1+x(x>0)得 ak+1=ln(eak-ak) >ln(1+ak-ak)=0, 这样0 由(1)(2)知,结论1成立. f(0)=0,f(1)=e-2.75<0, 由不等式ln(1+x) an+1=ln[1+(ean-1-an)] 2432设△ABC的三边长为a,b,c,对应的旁切圆半径分别为ra,rb,rc,则 (天津水运高级技工学校 黄兆麟 300456) 证明为书写简便,令∑表示三元循环和,且设待证不等式左右之差为M, 故命题成立. 2433如图,I是△ABC的内心,AI,BI,CI分别交外接圆于A1,B1,C1,R,r分别为△ABC外接圆与内切圆半径,求证: (Ⅰ)IA+IB+IC≤IA1+IB1+IC1 (1) (Ⅱ) 6r≤IA+IB+IC≤3R (2) (江西省九江市德安磨溪中学 胡文生 332000) 证明如下图,连接BA1,A1C,则BA1=A1C, 在△BA1C中,由正弦定理得 过点I分别作三边的垂线,垂足分别为D、E、F, 则ID=IE=IF=r, 且 故(1)式等价于 上式又等价于 (3) 和 =2x(y-x)+1-2[y2+x2-1+2(1-2x2)xy] =8x3y-4x2-2xy-2y2+3 =(1-4x2)(1-2xy)+2(1-y2) (4) 不妨设A≥B≥C≥0, 所以1-4x2≥0, 1-2xy≥0, 1-y2≥0, 从而 (4)≥0,即(3)式得证,也就是(1)式得证. 另一方面,由(1)式可得 2(IA+IB+IC) ≤(IA1+IA)+(IB1+IB)+(IC1+IC) =AA1+BB1+CC1≤2R+2R+2R=6R, 所以IA+IB+IC≤3R. 又由艾尔多斯—莫迪尔不等式得 IA+IB+IC≥2(r+r+r)=6r, 所以 6r≤IA+IB+IC≤3R, 即(2)式得证.当且仅当△ABC为正三角形时(1),(2)两式等号成立. 2434设正数a,b,c满足a+b+c=3,求证: (1) 其中“∏”表示轮换对称积 (四川成都金牛西林巷18号晨曦数学工作室宿晓阳610031) 证明由条件易知(1)式等价于 (2) 由对称性不妨设0 则b+c-a>0,c+a-b>0. 于是当a+b-c≤0时,(1)式显然成立. 当a+b-c>0时,则易知 (3) 事实上,(3)式等价于 4a2bc≥(b+c)2(c+a-b)(a+b-c) ⟺(a+b+c)(b+c-a)(b-c)2≥0, 此式显然成立.故(3)式成立. 同理 三式相乘并整理,即得(2)式. 综上所述(2)式得证.故(1)式成立. 2435设A,B,C为△ABC的内角,则 (陕西延安育英中学 尚生陈 716000) 2018年8月号问题 (来稿请注明出处——编者) (安徽省太和县第二小学 任迪慧 随礼敏 236630) (北京市陈经纶中学 张留杰 100020) 2438在△ABC中,设三内角A,B,C所对的三边长分别为a,b,c,三角形面积为Δ, (1) (河南质量工程职业学院 李永利 467000) 2439锐角三角形ABC各边AB,AC和BC分别被延长到点D,E,F,△ADE,△BDF和△CEF的外心分别为O1,O2,O3,如果∠DCA=90°,∠EFC=∠BAC,证明:△O1O2O3∽△ABC. (河南省辉县市一中 贺基军 453600) 2440令T={9k|k∈Z,1≤k≤2018},已知92018是1926位数 ,问T中有多少个元素以9为最左边的数字? (湖北省谷城县第三中学 贺斌 龚云峰 441700)