回归概念出新意 高屋建瓴追本质
——2018年高考北京卷压轴题的变式研究与启示
2018-10-16许绮菲
许绮菲
(北京市第一七一中学 100013)
考题再现
设n为正整数,集合A={α|α=(t1,t2,…,tn),tk∈{0,1},k=1,2,…,n}.对于集合A中的任意元素α=(x1,x2,…,xn)和β=(y1,y2,…,yn),记
(Ⅰ)当n=3时,若α=(1,1,0 ),β=(0,1,1),求M(α,α) 和M(α,β)的值;
(Ⅱ)当n=4时,设B是A的子集,且满足:对于B中的任意元素α,β,当α,β相同时M(α,β)是奇数;当α,β不同时,M(α,β)是偶数.求集合B中元素个数的最大值;
(Ⅲ)给定不小于2的n,设B是A的子集,且满足:对于B中的任意两个不同的元素α,β,M(α,β)=0.写出一个集合B,使其元素个数最多,并说明理由.
标准答案
(Ⅰ)因为α=(1,1,0 ),β=(0,1,1),
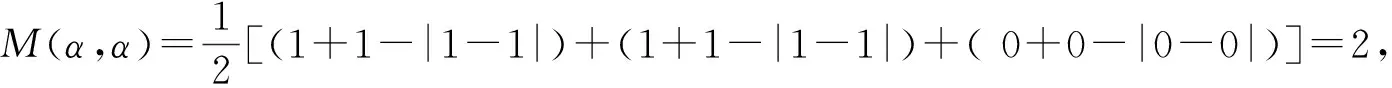
(Ⅱ)设α=(x1,x2,x3,x4) ∈B,则M(α,α)=x1+x2+x3+x4,
由题意知x1,x2,x3,x4∈{0,1},且M(α,α)为奇数,
所以x1,x2,x3,x4中1的个数为1或3.
所以B⊆{(1,0,0,0),(0,1,0,0),(0,0,1,0),(0,0,0,1),(0,1,1,1),(1,0,1,1),(1,1,0,1),(1,1,1,0)}.
将上述集合中的元素分成如下四组:
(1,0,0,0),(1,1,1,0);
(0,1,0,0),(1,1,0,1);
(0,0,1,0),(1,0,1,1);
(0,0,0,1),(0,1,1,1).
经验证,对于每组中两个元素α,β,均有M(α,β)=1,
所以每组中的两个元素不可能同时是集合B的元素,
所以集合B中元素的个数不超过4,
又集合{(1,0,0,0),(0,1,0,0),(0,0,1,0),(0,0,0,1)}满足条件,
所以集合B中元素个数的最大值为4.
(Ⅲ) 设Sk={(x1,x2,…,xn) | (x1,x2,…,xn)∈A,xk=1,x1=x2=…=xk-1=0,k=1,2,…,n)},Sn+1={(x1,x2,…,xn)|x1=x2=…=xn=0},
则A=S1∪S2∪…∪Sn+1.
对于Sk(k=1,2,…,n-1)中的不同元素α,β,经验证,M(α,β)≥1,
所以Sk(k=1,2,…,n-1)中的两个元素不可能同时是集合B的元素,
所以B中元素的个数不超过n+1.
取ek=(x1,x2,…,xn)∈Sk且xk+1=…=xn=0(k=1,2,…,n-1) ,
令B={e1,e2,…,en-1}∪Sn∪Sn+1,则集合B的元素个数为n+1,且满足条件,
故B是一个满足条件且元素个数最多的集合.
解法研究
本题源于2元域上n维线性空间的内积.题目的三个设问,难度逐步递增,但本质上环环相扣.第二问从第一问的事实和命题出发,将问题特殊化,在具体的数字计算中进一步寻求规律,引发大胆猜想;第三问从特殊拓展到一般,推出抽象情况的结论.问题由简入繁、前后衔接、逐步深入,试题考查学生抽象思维能力和创新解题能力,保持了北京数学试卷的新定义风格.
题目第一问帮助学生加强对新定义的理解,通过让学生计算当n=3,α=(1,1,0 ),β=(0,1,1)时M(α,α) 和M(α,β)的值引导学生在计算过程中发现规律,找到灵感为后续工作铺垫.
破解本题的关键是对题目中给出的如下新定义的本质理解:
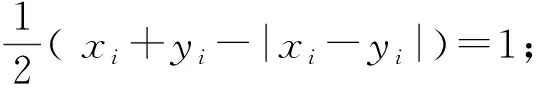
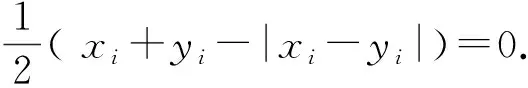
所以我们可以更通俗化地理解M(α,β)的定义:M(α,α) 记录了α这个n元有序数组中为1的个数;M(α,β)记录了α,β两个有序数组中对应项同时为1的项数.如α=(1,1,0 )中为1的项的个数为2个,则M(α,α)=2,当β=(0,1,1)时,α,β两个有序数组中对应项同时为1的项有一个,则M(α,β)=1.在这一“计数”视角下冗长的定义变得“亲切、自然”了.
下面在“计数”视角下解答第二问:
(Ⅱ)设α=(x1,x2,x3,x4) ∈B,由M(α,α)为奇数,得x1,x2,x3,x4中1的个数为1个或3个,所以B⊆{(1,0,0,0),(0,1,0,0),(0,0,1,0),(0,0,0,1),(1,1,1,0),(1,1,0,1),(1,0,1,1), (0,1,1,1)}.
将上述集合中的元素分成如下四组:
(1,0,0,0),(1,1,1,0);
(0,1,0,0),(1,1,0,1);
(0,0,1,0),(1,0,1,1);
(0,0,0,1),(0,1,1,1).
经验证,对于每组中两个元素α,β,有序数组中对应项同时为1项数均有1个,即M(α,β)=1不合题意,所以上述四组每组中的两个元素不可能同时是集合B的元素,集合B中元素的个数不超过4.
又集合{(1,0,0,0),(0,1,0,0),(0,0,1,0),(0,0,0,1)}满足条件,所以集合B中元素个数的最大值为4.
我们再以这一视角诠释第(Ⅲ)问:
(Ⅲ) 给定不小于2的n,设B是A的子集,且满足:对于B中的任意两个不同的元素α,β,M(α,β)=0,即对于集合B中任意两个元素α,β,有序数组中对应项不能同时为1,即任取元素α=(x1,x2,…,xn)和β=(y1,y2,…,yn),相应的xi,yi不能同时为1.
集合A={α|α=(t1,t2,…,tn),tk∈{0,1},k=1,2,…,n},将集合A中元素分为n+1个交集不全为空的集合:
P0:{(0,0,…,0)};
P1:{(x1,x2,…,xn) |x1=1,x2,x3,…,xn∈{0,1}};
P2:{(x1,x2,…,xn) |x2=1,x1,x3,…,xn∈{0,1}};
…
Pn:{(x1,x2,…,xn) |xn=1,x1,x2,…,xn-1∈{0,1}}.
对于P1,P2,…,Pn这n个集合,由集合B任意两个元素α,β,有序数组中对应项不能同时为1,故每个集合至多取一个元素:
pi=(x1,x2,…,xn)∈Pi,x1=x2=…=xi-1=xi+1=…=xn=0,i=1,2,…,n,共有n个元素.
又(0,0,…,0)∈A,则集合B的元素个数最多为n+1个.
变式思考
在解法研究过程中,我们给新定义:
赋予一个学生容易理解的“计数”情境,在这一情境下使解法生动起来.
至此我们不禁联想到2010年高考数学北京卷20题:
已知集合Sn={X|X=(x1,x2,…,xn),xi∈{0,1},i=1,2,…,n}(n≥2),对于A=(a1,a2,…,an),B=(b1,b2,…,bn),
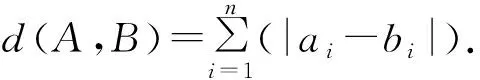
证明:(Ⅰ)∀A,B,C∈Sn,有A-B∈Sn,且d(A-C,B-C)=d(A,B);
(Ⅱ)∀A,B,C∈Sn,d(A,B),d(A,C),d(B,C)三个数中至少有一个是偶数;
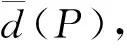
这个题目同样有高等代数的背景,文[1]从“距离”等角度给出了一个不同于标准答案的解法.我们再从“计数”的角度思考如下:
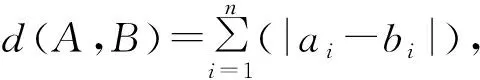
(Ⅰ)设C=(c1,c2,…,cn),关注三个有序数组中的对应项ai,bi,ci∈{0,1},当ai,bi相同时,|ai-bi|=0,而ai-ci,bi-ci也相同,即|(ai-ci)-(bi-ci)|=0;当ai,bi不同时,|ai-bi|=1,而ai-ci,bi-ci也不同,|(ai-ci)-(bi-ci)|=1.
从“计数”视角显然d(A-C,B-C)=d(A,B).
(Ⅱ)∀A,B,C∈Sn,不妨设A与C这两个有序数组中不同的对应项的个数为p个,即d(A,C)=p,设B与C这两个有序数组中不同的对应项的个数为q个,即d(B,C)=q,若p,q中至少有一个为偶数则题设得证.当p,q均为奇数时,若A、C这两个有序数组中不同的对应项与B、C这两个有序数组中不同的对应项没有“重叠”,由ai,bi,ci∈{0,1}可知,A与B这两个有序数组中不同的对应项的个数为p+q个,显然p+q为偶数,即d(A,B) 为偶数;若A与C这两个有序数组中不同的对应项与B、C这两个有序数组中不同的对应项有k个位置“重叠”,易知A、B这两个有序数组中不同的对应项的个数为p+q-2k个,即d(A,B) 为偶数.命题得证.
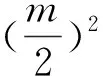
以“计数” 这一学生较为熟悉的情境,行云流水般地解决了2018年20题与2010年20题,体现了数学创新思维的优秀品质和较高的数学素养.
试题启示
近年来,北京高考数学试卷注重加强对数学核心素养和关键能力的考查,特别是理科第20题因其知识起点低、背景深刻、思维灵活、知识面广,一直以来受到中学师生的广泛关注.北京卷20题虽然所涉及的数学背景有优化理论、数论、高等代数等,但并不需要学生掌握超出课程标准要求之外的数学知识,考查的是学生通过中学阶段数学基础知识的学习,正确理解抽象的数学概念,在逻辑推理的基础上进行数学符号化表征的能力.重点考查数学抽象和逻辑推理能力等核心素养.
我们并不倡导通过奥数及AP先修课程学习去求解高考北京卷20题.教师在教学中注重与学生一起给抽象的问题创设一个较容易接受的情境,使学生在与教师共同探究的过程中对一些情境留有较为深刻的印象,在思维不断碰撞中激励学生,通过典型例子的分析和学生自主探究活动,使学生理解数学概念、结论逐步形成的过程,体会蕴含在其中的思想方法.教师要努力创设生动活泼的问题情境,揭示数学概念、法则、结论的发生、发展过程,掌握其本质,把数学的学术形态转化为学生易于接受的教育形态,使学生看到题目后能逻辑连贯地、前后一致地进行数学思考,并用较严谨有序的数学语言表述其思维过程,这是破解北京高考数学20题的基本策略.
