十年高考全国课标卷统计与概率解答题的考查研究
——以2009年至2018年高考全国课标卷理科为例
2018-10-16宋建辉
宋建辉
(福建省福州格致中学 350001)
1 引言
统计与概率是高中数学的重要内容,《2018年普通高等学校招生全国统一考试大纲的说明(理科)》对统计与概率内容的要求是,高考主要考查随机抽样,用样本估计总体,变量的相关性,随机事件的概率,古典概型,几何概型,回归分析,独立性检验,离散型随机变量的分布列、期望、方差,正态分布.考查重点是用样本估计总体,古典概型,离散型随机变量的分布列、期望、方差,应用回归分析与独立性检验思想方法解决简单实际问题的能力.试题强调应用性,以实际问题为背景,构建数学模型,突出考查统计与概率的思想和考生的数据处理能力以及应用意识.
本文将以2009年至2018年高考全国课标卷统计与概率(理科)解答题为例,对其进行一次理论与实践的总结和分析,与大家分享试题背后的思想和试题对教学的引导作用,希望能给一线教师提供一点经验.
2 基本情况分析
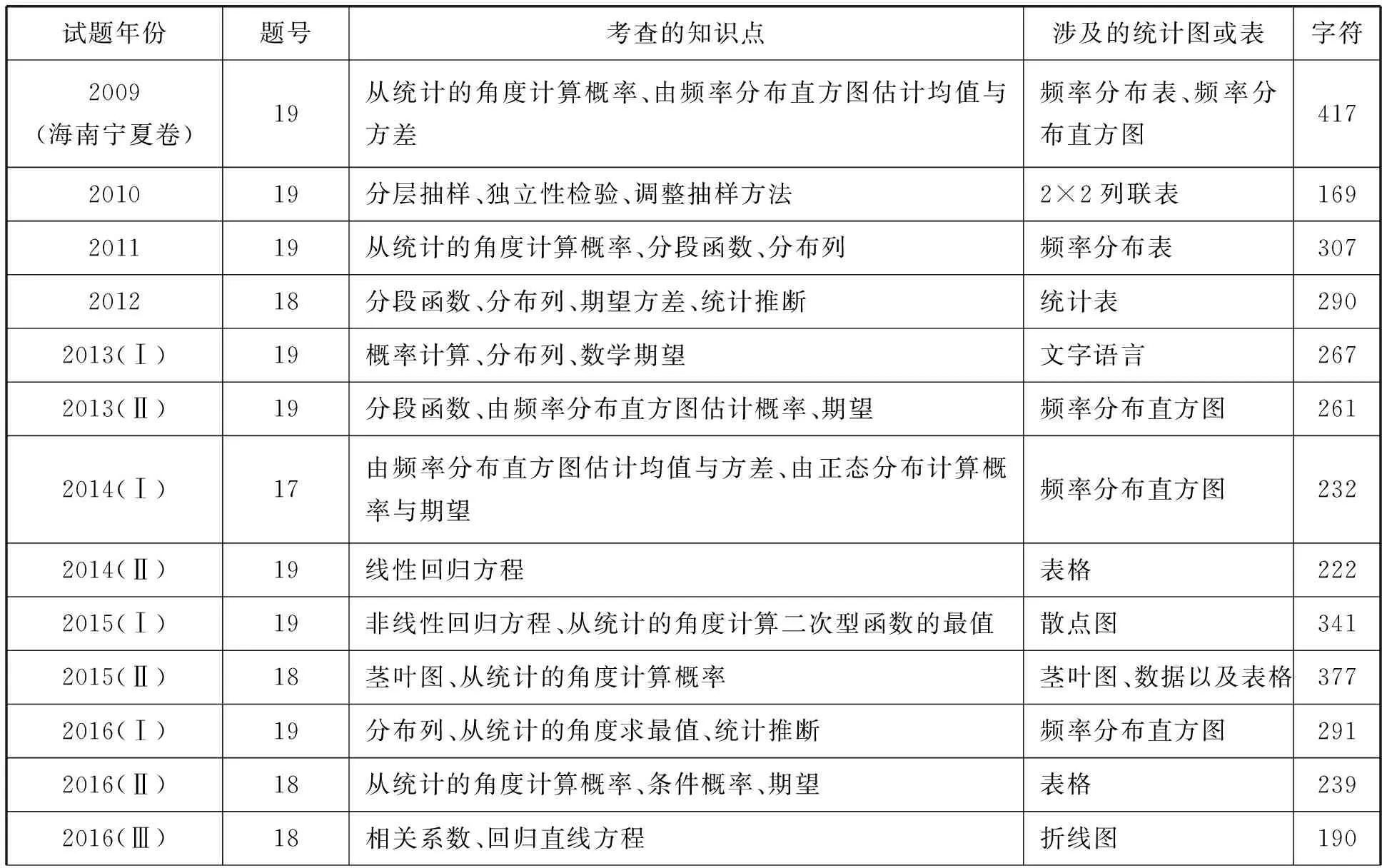
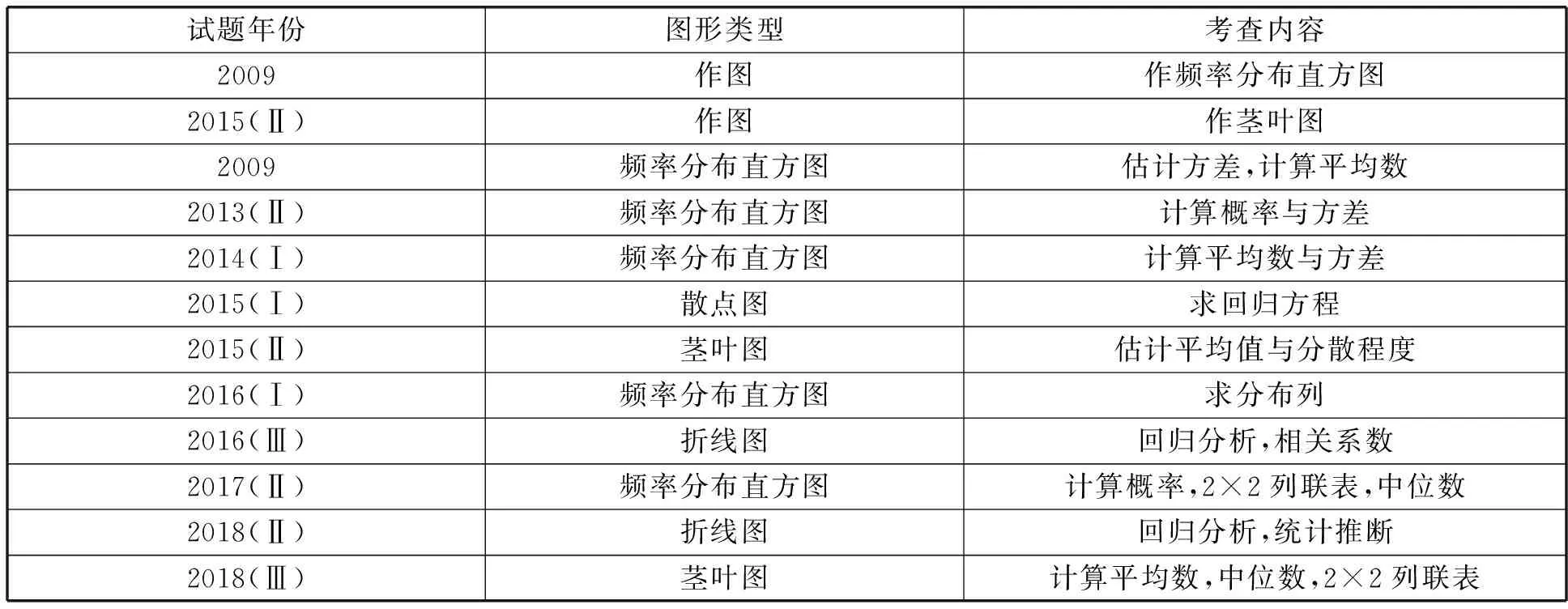
表1 2009年至2018年高考课标卷统计与概率解答题统计

续表
由表1,统计与概率命题范围主要有:用样本估计总体,离散型随机变量的分布列、期望与方差,正态分布,回归分析与独立性检验,统计决策,并多次与函数结合在一起考查.其基本情况有如下4点:
①从题号来看,除了2014年Ⅰ卷和2018年Ⅰ卷外,其余均是解答题的第18或19题,属中档和中档偏上的题目.但从实测数据来看,以福建省2016年和2017年公布的数据:2016年难度0.34,2017年难度0.24,由此可以看到课标卷的统计概率题难点在于“新”.
②除了2013年Ⅰ卷和2018年Ⅰ卷外,所有题目都与统计图表紧密相连,涉及频率分布直方图、茎叶图、折线统计图、散点图,读图识表作图是基本要求.
③不含空格,从统计的字符来看,信息量相当大,需要很好的数学阅读能力.
④大部分考查离散型随机变量分布,尤其是超几何分布与二项分布,其中2014年Ⅰ卷与2017年Ⅰ卷结合正态考查二项分布.
十年所考的19题对统计与概率的知识、思想、能力进行了非常全面的考查,强调应用性,试题呈现出三大特点:
(1)背景公平,控制难度.全国卷的统计与概率解答题主要是以考数学应用题的考查目标而出现的,因此它必须以大多数考生熟悉的社会热点问题为背景才能显示公平,而且考查的难度适中.
(2)以统计为主,概率为辅.在命题设计中,对概率的考查基本上都是从统计的角度来计算概率,即概率计算是为统计服务的,重在强调对统计的基本思想方法及其应用的考查,重在利用统计与概率思想解决实际问题.
(3)强调对随机模型的建立,统计数据的收集、整理和处理,直至最终作出相关统计决策的全过程的考查.
3 试题分析
3.1 突出统计概率思想分析、解释和统计决断
统计与概率思想包含统计思想与概率思想两个部分,统计思想是指利用统计数据,依据统计问题的要求,得到统计结论;概率思想是通过对随机现象的观察研究发现必然,去研究隐藏在随机现象背后的统计规律,进而理解随机现象.
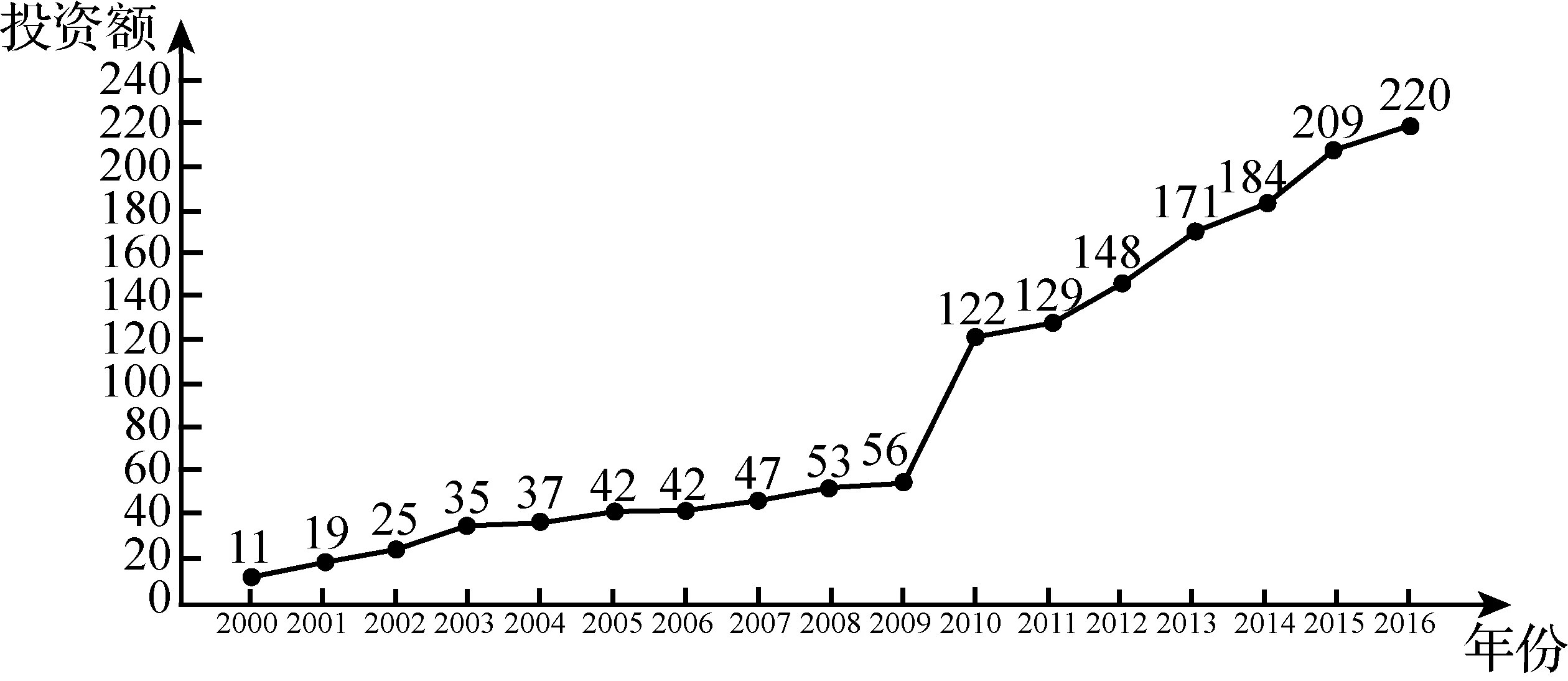
例1(2018全国1卷理20)某工厂的某种产品成箱包装,每箱200件,每一箱产品在交付用户之前要对产品作检验,如检验出不合格品,则更换为合格品.检验时,先从这箱产品中任取20件作检验,再根据检验结果决定是否对余下的所有产品作检验.设每件产品为不合格品的概率都为p(0 (1)记20件产品中恰有2件不合格品的概率为f(p),求f(p)的最大值点p0; (2)现对一箱产品检验了20件,结果恰有2件不合格品,以(1)中确定的p0作为p的值.已知每件产品的检验费用为2元,若有不合格品进入用户手中,则工厂要对每件不合格品支付25元的赔偿费用. (i)若不对该箱余下的产品作检验,这一箱的检验费用与赔偿费用的和记为X,求EX; (ii)以检验费用与赔偿费用和的期望值为决策依据,是否该对这箱余下的所有产品作检验? (2)(i)剩余180件产品中恰有Y件是不合格品服从二项分布B(180,0.1),所以检验费用与赔偿费用的和X=25Y+40,则EX=E(25Y+40)=490. (ii)如果对余下的产品作检验,则这一箱产品所需要的检验费为400元,由于EX>400,故应该对余下的所有产品作检验. 本题以统计思想为引导,从统计的角度求得概率,让概率为统计服务,考查样本估计总体的思想,考查统计思维.课标卷的统计概率解答题尤其突出统计概率思想分析问题、解释问题和统计推断,充分体现了高考的考查重点是利用统计与概率思想解决实际问题,体现了数学的应用性价值.十年高考题中具有“统计决断”特征的试题如下: 表2 统计决断问题统计 数据处理能力是指会收集数据、整理数据、分析数据,能从数据中提取对研究问题有用的信息,并做出合理判断.数据处理能力主要是针对研究对象的特殊性,选择合理的收集数据的方法,根据问题的具体情况,选取合适的统计方法整理数据,并构建模型对数据进行分析、推断,获得结论.数据处理能力要求学生能理解问题所提供的文字、数字、图形、图表等信息,并能从中提取有关信息,对它们进行分析和处理.能对有关的数据和图形进行统计和分析,应用统计或统计案例中的方法解决实际问题. 例2(2017全国1卷理19)为了监控某种零件的一条生产线的生产过程,检验员每天从该生产线上随机抽取16个零件,并测量其尺寸(单位:cm).根据长期生产经验,可以认为这条生产线正常状态下生产的零件的尺寸服从正态分布N(μ,σ2). (1)假设生产状态正常,记X表示一天内抽取的16个零件中其尺寸在(μ-3σ,μ+3σ)之外的零件数,求P(X≥1)及X的数学期望; (2)一天内抽检零件中,如果出现了尺寸在(μ-3σ,μ+3σ)之外的零件,就认为这条生产线在这一天的生产过程可能出现了异常情况,需对当天的生产过程进行检查. (ⅰ)试说明上述监控生产过程方法的合理性; (ⅱ)下面是检验员在一天内抽取的16个零件的尺寸: 9.9510.129.969.9610.019.929.9810.0410.269.9110.1310.029.2210.0410.059.95 简解(1)由正态分布知一个零件的尺寸在(μ-3σ,μ+3σ)之外的概率为0.0026,再由独立重复试验的概率模型可知故X服从二项分布B(16,0.0026),从而P(X≥1)=1-P(X=0)=1-0.997416=0.0408,EX=16×0.0026=0.416. (2)(ⅰ)如果生产状态正常,零件尺寸服从正态分布,那么零件在(μ-3σ,μ+3σ)之外取值的概率只有0.0026.抽取的16个零件中,出现尺寸在(μ-3σ,μ+3σ)之外的概率只有0.0408,发生的概率很小.这样小概率事件在实际中几乎不会发生.一旦发生这种情况,就有理由认为这个事件不是小概率事件,即可推断零件尺寸不服从正态分布,也就是说生产状态不正常,即这条生产线在这一天的生产过程可能出现了异常情况,需对当天的生产过程进行检查,可见上述监控生产过程的方法是合理的. 本题充满了创新性,数据处理问题是该题的另一个亮点,从大量数据中对研究问题提取出有用的信息,构建“随机抽样一收集数据一整理、分析数据一提取信息一用信息去说明问题”的框架.在统计问题中,数据的获得是至关重要的.此题用给出的数据,灵活的考查了相关知识,尤其第(ⅱ)小题,在原有16个数据平均数和标准差考查去掉一个数后的平均数标准差,用数据说话,也是每年高考概率与统计试题之中的有效考查方式. 课标卷的统计与概率解答题分别以“频率分布直方图”、“茎叶图”、“折线统计图”、“统计表”和“文字语言”不同方式呈现对数据处理能力的考查,考查的知识点也各不相同,但从考查的“数据处理能力”来看,思路一直没有改变,且不断加强.无论是哪种方式呈现,数据都是含有信息的,根据数据的特点选择不同的计算方式以及对公式或数据进行变形和对参考数据的解读,这些都是最基本的,所以与数据处理能力相伴而生的是对数据的解读和对数据或公式的变形应用,体现了数据分析的核心素养. 从表1的统计来看,所有试题都与统计图表紧密相连,突出考查“读图识图”的应用意识和能力,另外统计与概率中有大量的数据与图形相关,要能够识图处理数据.主要类型如下表所示: 表3 统计图类型统计 例3(2018全国2卷理18)下图是某地区2000年至2016年环境基础设施投资额y(单位:亿元)的折线图. (1)分别利用这两个模型,求该地区2018年的环境基础设施投资额的预测值; (2)你认为用哪个模型得到的预测值更可靠?并说明理由. (2)利用模型②得到的预测值更可靠. (ⅱ)从计算结果看,相对于2016年的环境基础设施投资额220亿元,由模型①得到的预测值226.1亿元的增幅明显偏低,而利用模型②得到的预测值的增幅比较合理.说明利用模型②得到的预测值更可靠. 以上给出了2种理由,考生答出其中任意一种或其他合理理由均可得分. 本题背景源于社会生活的实际,要求考生读懂该统计图,从统计图中获得相关的信息,问题的设置很人性化,通俗易懂,有利于考生分析、解决问题.本题注重对数学素养和能力的考查,在引导中学加强“数学应用能力和应用意识”的教育培养方面具有很好的引导作用,堪称“读图识图”的典范. 概率计算问题,从课标卷来看,既注重计算概率的基本根据计数原理的应用,更注重从统计的观点来计算概率,尤其在统计与概率的解答题中体现的淋漓尽致,是新课标思想的极致体现. 考试大纲在考查要求上开门见山地强调了知识交汇,与函数相结合考查是课标卷的统计与概率解答题又一特色之一,试题的设计注重学科的内在联系和知识的综合性,从学科的整体高度和思维价值的高度考虑问题,将交汇的特色突出地彰显. 表5 与函数结合统计 随着人们对统计在决策中的作用的认识的深入,课标卷中加大了对统计内容考查的力度.课标卷统计与概率的命题,从数学学科的整体高度和思维能力的角度出发,将知识、能力与素养融为一体,全面考查了学生的数学能力与素养,试题注重了数学的学科特点,突出了知识的基础性和综合性,以知识为主体,顺应时代需求,在知识交汇处设计试题,使对统计概率的基础知识的考查达到了必要的深度和广度,以此来推动概率统计思想在中学教学中的渗透和发展. 本文以2009年至2018年高考全国课标卷理科为例,把十年课标卷的统计与概率内容进行了一次较为系统的总结与分析,详细阐述了近几年统计与概率解答题的探索与改革方向,以及试题背后蕴含的统计思想,以期让一线教师更加了解试题的设计初衷,为更好地进行统计与概率的教与学提供了一个参考框架.本人水平有限,如有不当之处请批评指正.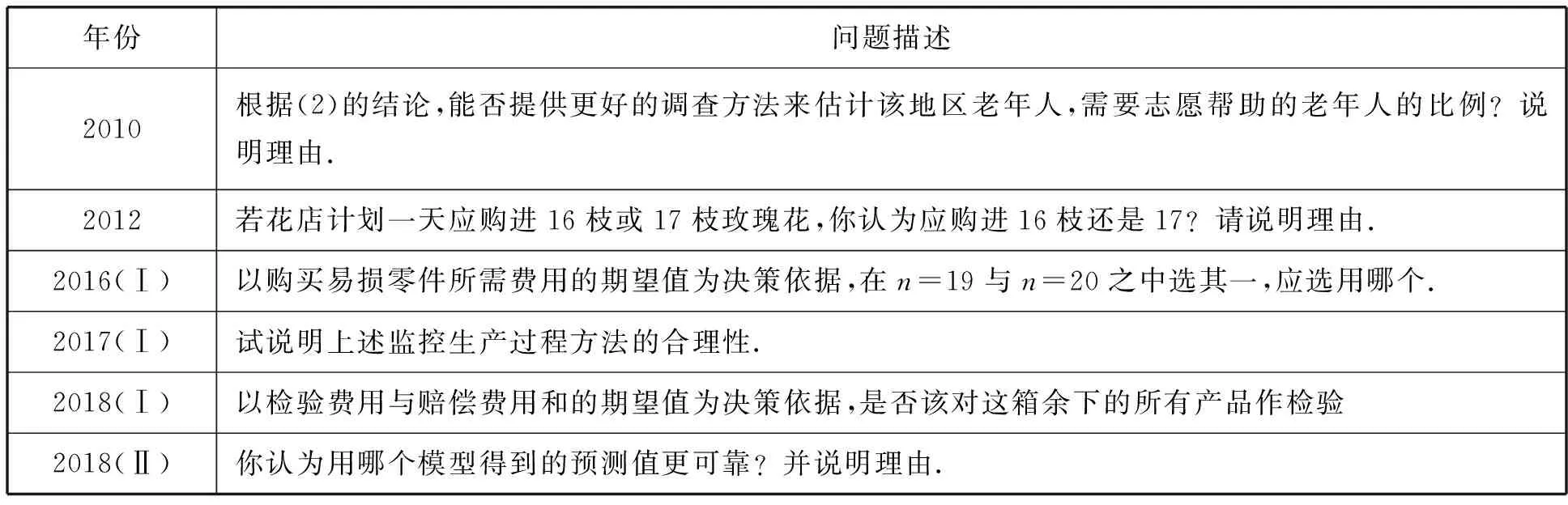
3.2 对数据处理能力提出了较高要求

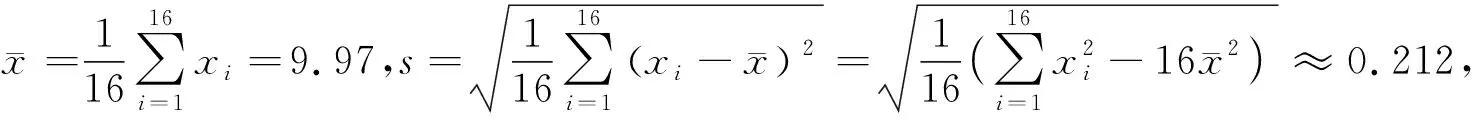
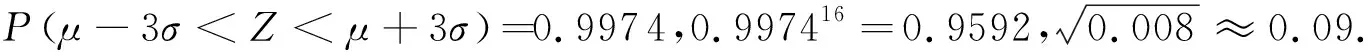
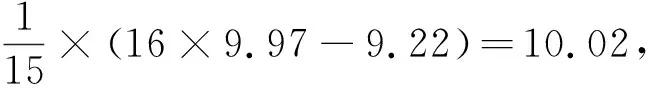
3.3 作图读图识图提到了非常重要的位置
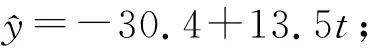
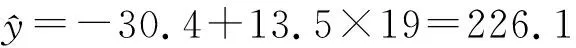
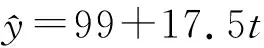
3.4 从统计的角度计算概率
3.5 注重综合考查,关注知识交汇
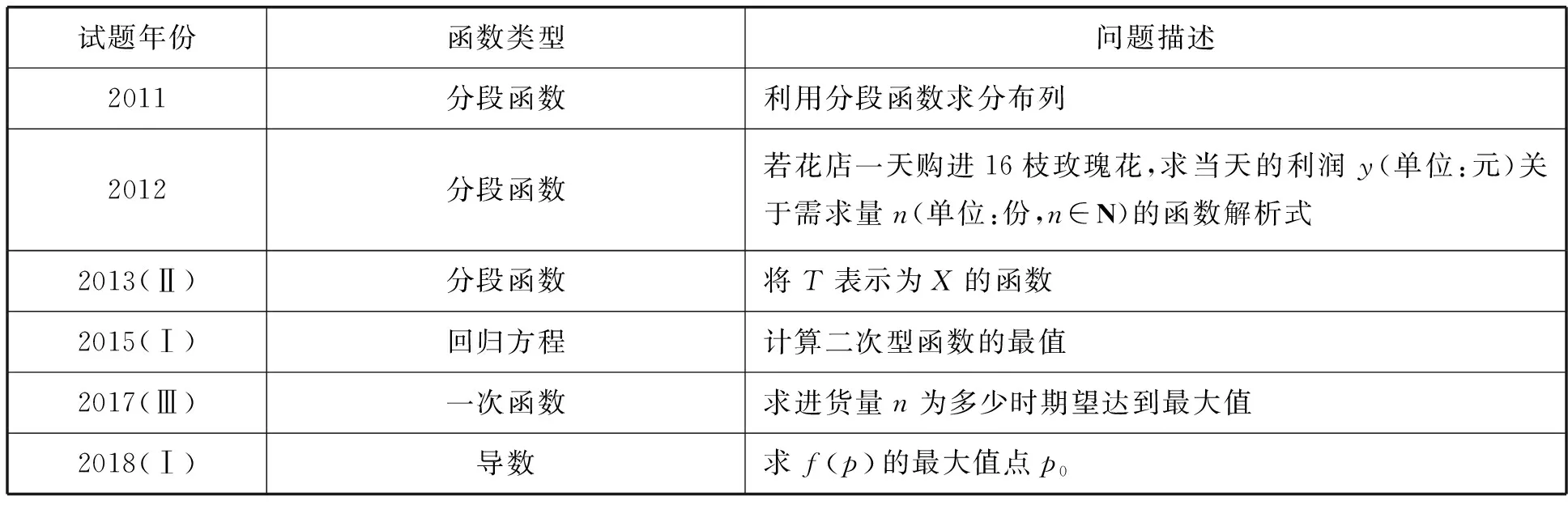
4 结语
