基于混杂非对称复合材料的自适应对日定向器

2018-10-13陆国平周徐斌

宇航学报 2018年9期

江霆,李昊,陆国平,王彦,周徐斌

(上海卫星工程研究所，上海 201109)

0 引言

近年来，随着航空技术的发展，智能可变形结构由于其优越的性能正受到越来越多的关注，智能可变形结构通常能够通过改变其形状来适应不同的外部条件，最常见的如可变形机翼。目前大多数智能可变形结构通过利用智能材料，如压电材料[1]或形状记忆材料来驱动结构偏离其平衡位置以发生变形[2]。这些可变形结构通常需要持续的能量输入来维持结构的变形，因此需要在变形体系中植入一定的加载设备、控制设备和载荷维持设备等，这必然会大大增加结构的重量，不利于可变形结构在航空航天领域上的应用[3]。

卫星在静止轨道运行时所需能量主要由太阳能翼提供。面积一定的太阳翼提供能量的大小主要取决于其法线方向和太阳矢量方向之间的夹角β。β越小，其吸收太阳光辐射能量的有效面积越大，效率越高，输出功率越大。国内外卫星太阳翼对日定向的方式主要包括固定展开式、单自由度驱动、单自由度加偏置角、双自由度驱动、三自由度驱动等驱动方式。目前，国内外最常采用的定向方式是单自由度对日定向方式。卫星在静止轨道运行时，太阳翼上太阳光入射角变化主要由两方面因素造成：一是卫星随地球自转；二是卫星随地球绕太阳公转。前者导致太阳光入射角的变化属于快变化，后者导致太阳光入射角变化属于慢变化。单自由度对日定向方式解决了快变化问题，而忽略了慢变化问题。单自由度加偏置的方式不仅解决了太阳光入射角快变化问题，也通过调整卫星姿态的方式解决了太阳光入射角慢变化问题。然而，通过该方法实现太阳翼对日定向会对某些卫星有效载荷功能的实现产生影响，如对地观测卫星。

单向碳纤维增强预浸料在垂直于纤维方向的热膨胀系数远大于沿纤维方向的热膨胀系数，因此在非对称层合板或混杂金属层非对称层板中，由于铺层之间残余热应变不匹配，导致非对称层板在固化后内部产生较大的残余热应力，进而产生明显的固化变形[4]。试验及理论研究显示，非对称复合材料层合板随着温度的变化将产生大变形，因此非对称层板可同时作为承载结构和变形构件，其在可变形结构上的应用已引起国内外学者的关注[5-12]。本文基于混杂非对称复合材料结构热变形提出并设计了一种新型太阳翼自适应对日定向器，通过利用日照变化引起的混杂非对称复合材料结构温度变化，进而混杂非对称复合材料结构产生大变形并驱动太阳翼转动，解决太阳光入射角慢变化问题。该定向器结合电机驱动的单自由度定向器，可以实现太阳翼的双自由度对日定向。

本文首先建立混杂非对称层合板的热变形预测模型，构建基于非对称混杂层合板的自适应转动机构并分析其变形及转动特性；在第三部分，本文基于地球静止轨道(GEO)的光照条件，分析自适应对日定向器的温度变化并计算其转动角度；在第四部分本文对自适应对日定向器的关键设计参数进行分析，并给出一种自适应对日定向器的优化方案，使得GEO轨道上太阳能帆板法向与阳光之间最大夹角始终小于±1°，满足±2°的性能指标要求。

1 非对称复合材料结构热变形分析

本节采用Rayleigh-Ritz法建立混杂非对称复合材料层合板的大变形理论预测模型，分析层合板温度变形特性，同时采用有限元的方法对其进行分析，对两者的分析结果进行比较。

1.1 复合材料结构热变形分析模型

取层合板中面为x-o-y坐标面，z轴垂直于板中面，z轴取向上为正，混杂非对称层合板分析坐标系如图1所示。层合板第k层位于厚度方向zk与zk+1之间，zk+1-zk=tk,tk表示第k层厚度。经典层合板理论指出复合材料层合板第k层应变为：

εk=ε0+zκ

(1)

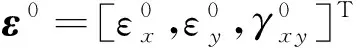
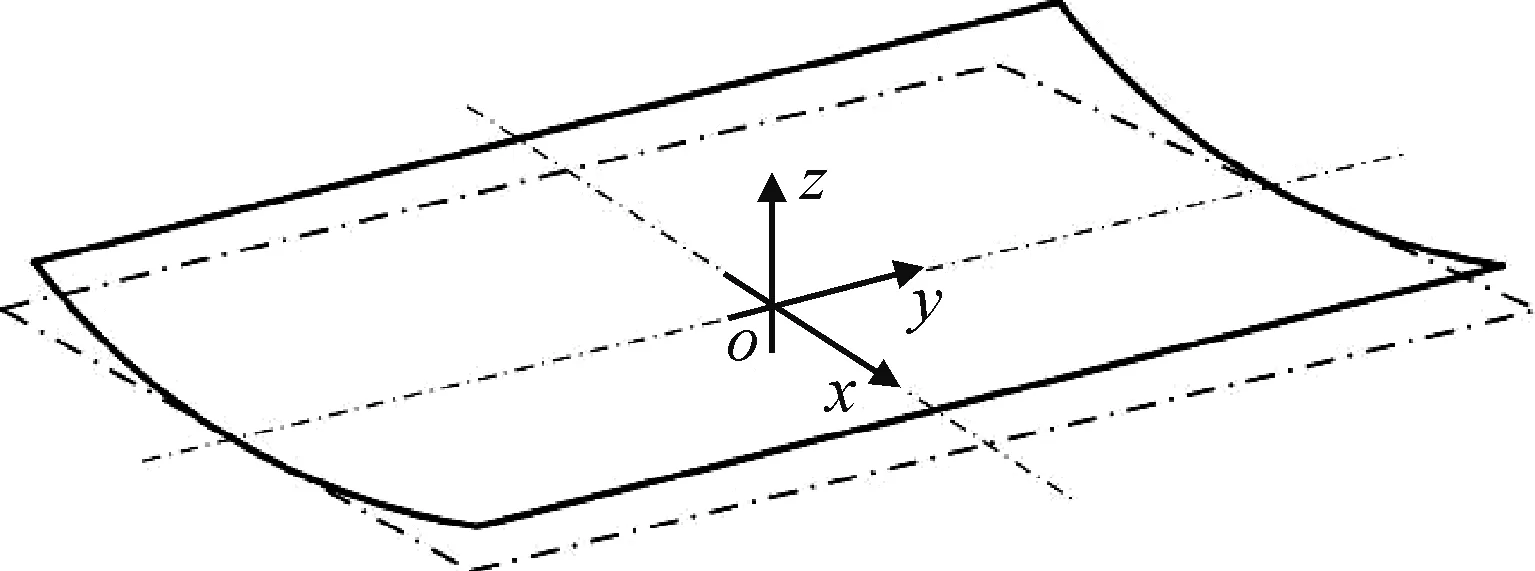
图1 混杂非对称层合板分析坐标系Fig.1 The coordinate system of analyzing hybrid asymmetric laminates

对于混杂非对称复合材料层合板非线性大变形，中面应变与中面位移关系可表示为

(2)

单位长度层合板上的合力和合力矩为

(3)

式中：Δκ=κ-κ0=[κx-κx 0,κy-κy 0,κxy-κxy 0]T表示中面曲率变化量，κ0=[κx 0,κy 0,κxy 0]T表示初始中面曲率。A，D，B分别表示面内刚度矩阵，弯曲刚度矩阵，耦合刚度系数矩阵。

层合板热合力和热合力矩为：

(4)

(5)

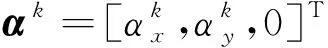
(6)

则中面应变及中面曲率为

(7)

(8)

式中：ɑ，b，c，d均为常数。

层合板残余合力和残余合力矩分别为：

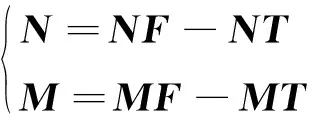
(9)

设混杂复合材料层合板宽为Lx,长度为Ly,则混杂复合材料层合板的总应变能：

NTε0-MTΔκ)dy]dx

(10)

根据能量变分原理，将式(10)分别对ɑ，b，c,d求偏导，并令其为0，得：

(11)

求解式(3)～式(11)可以得到ɑ，b，c，d的值，即中面应变ε0及中面曲率κ。式(11)通常存在多组解，因此必须对计算结果稳定性进行分析，即雅可比矩阵必须为正定矩阵：

(12)

1.2 复合材料结构热变形分析结果

混杂复合材料铺层材料选择碳纤维/环氧树脂及铝合金，材料具体参数见表1。层合板的固化温度为T0=180℃，采用第1.1节的热变形模型及有限元方法分析50 mm×100 mm，初始曲率κ0=[0,0,0]T，[Alt=0.5 mm/Ct=0.5 mm]复合材料层合板恢复到常温T=20 ℃时的形状。

表1 混杂复合材料层合板铺层材料属性Table 1 Hybrid composite laminate material properties

采用ABAQUS建立有限元模型，模型采用S4R壳单元，单元数量200。分析结果如图2所示，图中黑色点代表FEA预测值，网格表示理论模型预测值。图2表明理论模型的预测结果与有限元模型的预测结果吻合很好。在内部残余热应力的作用下，[Alt=0.25 mm/Ct=0.25 mm]复合材料层合板沿着x方向弯曲。

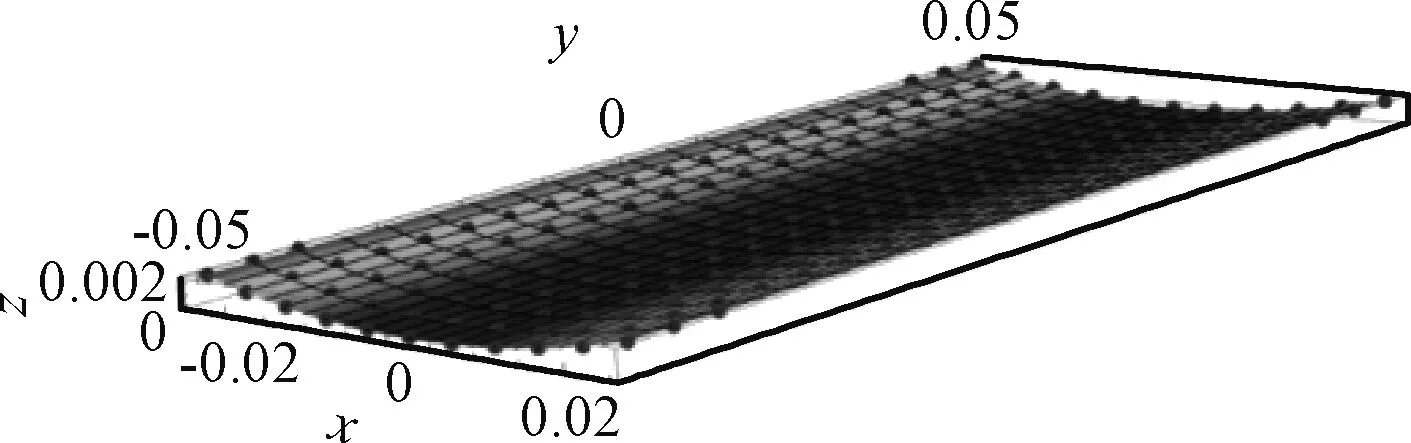
图2 50 mm×100 mm混杂复合材料层合板变形预测结果(T=20 ℃)Fig.2 Prediction results of the deformation of 50 mm×100 mm composite laminate(T=20 ℃)

假设混杂复合材料层合板的初始曲率为κ0=[κx 0,0,0]T。分别分析κx 0=25 m-1和κx 0=50 m-1时，层合板在常温(T=20 ℃)下的变形，变形结果如图3和图4所示。混杂复合材料层合板的弦长变形：

(13)

图3及图4中，理论模型所预测的弦长变形量Δx与有限元模型预测结果相比误差分别4.49%和2.40%。

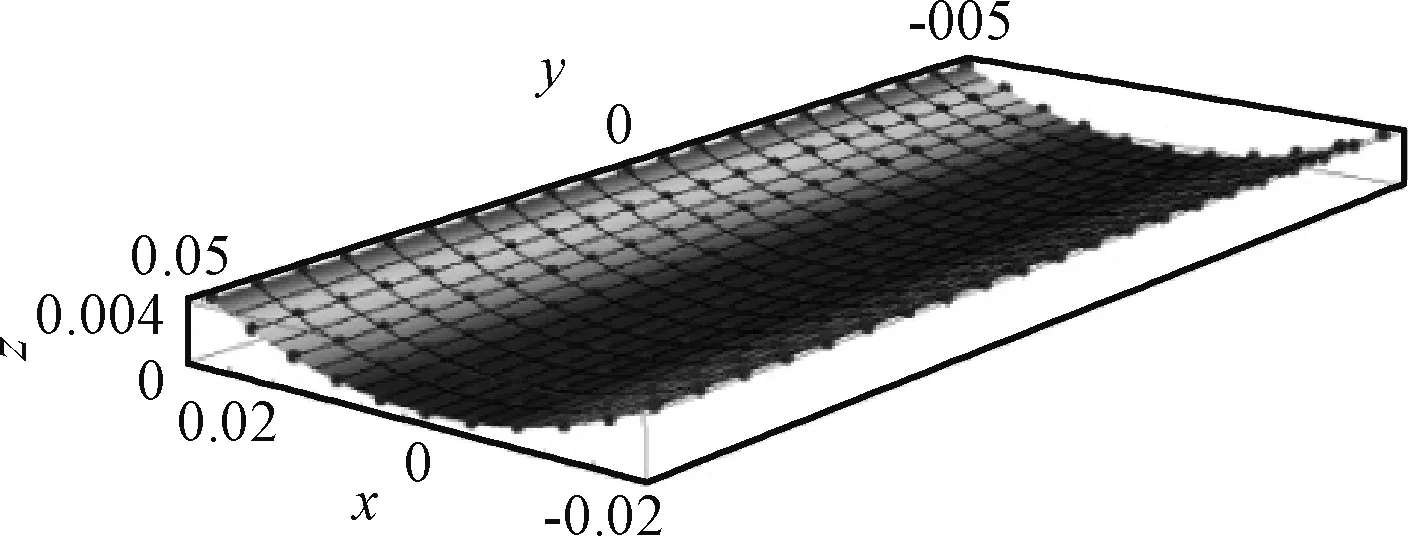
图3 50 mm×100 mm，κx 0=25 m-1混杂复合材料层合板变形预测结果(T=20 ℃)Fig.3 Prediction results of the deformation of 50 mm×100 mm, κx 0=25 m-1 composite laminate(T=20 ℃)

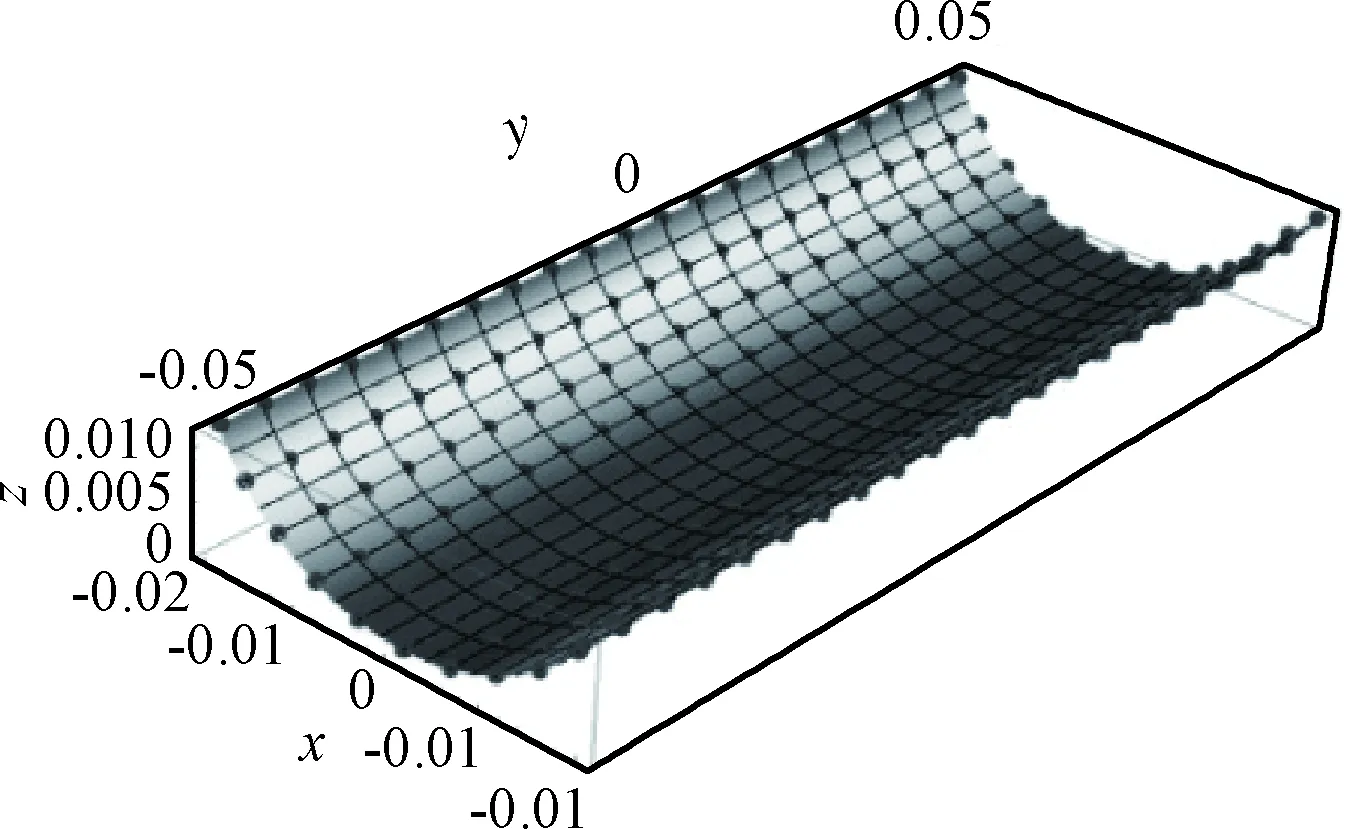
图4 50 mm×100 mm，κx 0=50 m-1混杂复合材料层合板变形预测结果(T=20 ℃)Fig.4 Prediction results of the deformation of 50 mm×100 mm, κx 0=50 m-1 composite laminate(T=20 ℃)

当温度层合板的在-100～250℃变化时，不同初始曲率的层合板弦长变形随温度变化曲线Δx-T的预测结果如图5所示。计算结果显示，在-100～180 ℃范围内，50 mm×100 mm，[Alt=0.25 mm/Ct=0.25 mm]初始曲率(初始弯曲弧度)越大，其在x方向上的弦长变化量越大。初始曲率为50 m-1(初始弯曲弧度为π)时，50 mm×100 mm的[Alt=0.25 mm/Ct=0.25 mm]层合板弦长在x方向变形量达到其初始弦长的11.16%。

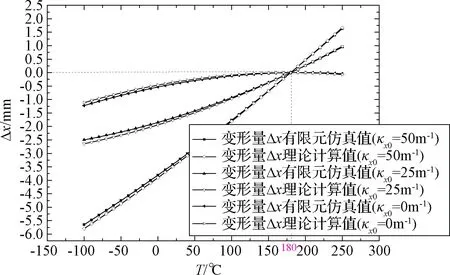
图5 不同初始曲率50 mm×100 mm [Al/C]层合板弦长变形Δ x-T曲线Fig.5 Relationship between chord length deformation of 50 mm×100 mm [Al/C] laminate board and initial curvature

2 自适应对日定向器原理

前文分析表明，混杂非对称复合材料[Al/C]层合板的温度发生变化时，在内部热应力的作用下，将产生大变形，且相同尺寸的层合板，变形量随初始弯曲弧度(初始曲率)的增大而增大。本文选择层合板初始弯曲弧度为π，并基于混杂非对称复合材料[Al/C]层合板变形-温度相关性，提出了一种基于[Al/C]层合板的太阳翼自适应对日定向机构。对日定向机构的驱动单元如图6所示，太阳翼自适应对日定向机构示意图见图7。

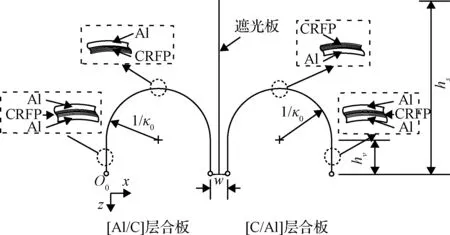
图6 转动机构驱动单元示意图Fig.6 Schematic diagram of drive unit of rotary mechanism

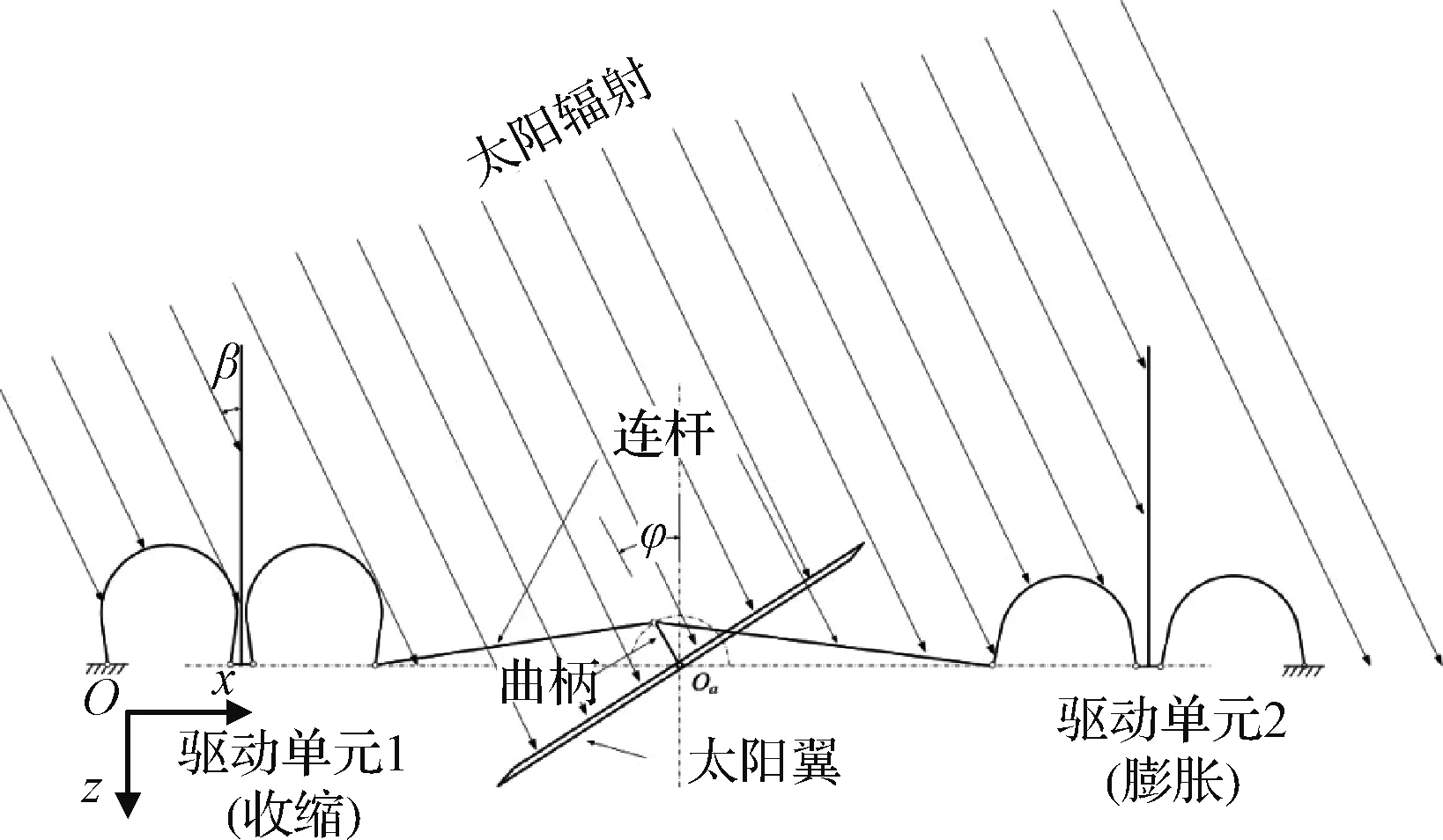
图7 太阳翼转动机构示意图Fig.7 Diagram of solar wing rotating mechanism

对日定向机构的驱动单元由两块半圆形混杂非对称复合材料层合板串联而成，串联的两个层合板之间安装一块遮光板。非对称层合板铺层数为两层，材料采用金属铝和碳纤维/环氧树脂。碳纤维/环氧树脂层采用单向预浸料沿层合板弯曲方向铺设，铺层角度为0°。在单个驱动单元中，两块混杂复合材料层合板的铺层顺序不同，分别为[Al/C]和[C/Al]。对于非对称铺层的[Al/C]层合板和[C/Al]层合板，当层合板温度均升高时，[Al/C]层合板将发生收缩，[C/Al]层合板将发生膨胀；相反，当温度均降低时，[Al/C]层合板将发生膨胀，[C/Al]层合板将发生收缩。图7中驱动单元 1和驱动单元 2对称设置。从左至右，驱动单元 1和驱动单元 2中层合板设置为[Al/C]，[C/Al]，[C/Al]及[Al/C]。当太阳光从左侧照射时，由于遮光板的存在，驱动单元 1和驱动单元 2的左侧层合板温度升高，右侧层合板温度降低。根据混杂非对称层合板变形与温度的关系，驱动单元 1整体表现为收缩，驱动单元 2整体表现为膨胀，两者的变形及产生的驱动力最终驱动连杆带动曲柄转动，实现太阳翼的对日定向。基于自适应对日定向器的双自由度太阳翼效果图如图8所示。

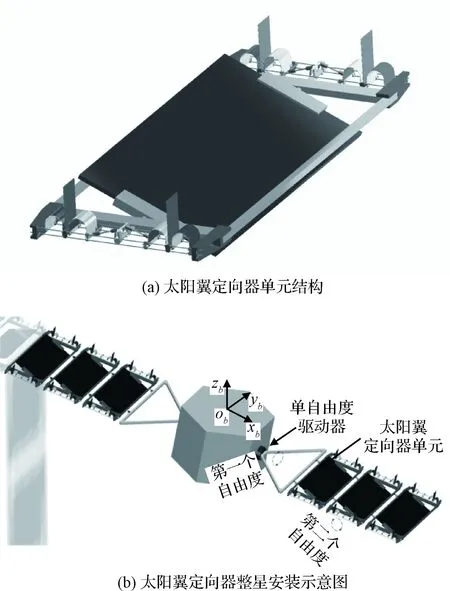
图8 基于自适应对日定向器的双自由度太阳翼Fig.8 The solar wing having two-degree of freedom based on adaptive sun tracker

3 对日定向器驱动位移分析

本文以尺寸为700 mm×340 mm×10 mm的太阳翼单元帆板为驱动目标进行对日定向器设计和研究。根据帆板的尺寸，在考虑满足安装空间及机构运动不发生干涉的条件下，选择半圆形混杂非对称复合材料层合板x方向弦长为40 mm,即初始曲率κx0=50 m-1，初始状态[Ct=0.5 mm/Alt=0.5 mm]层合板结构的右侧到轴O的距离D=64 mm。

本文基于地球静止轨道空间热环境进行自适应对日定向器设计[15-16]。在传统单自由度驱动机构作用下，从冬至日至夏至日，太阳光与太阳翼法向夹角β的变化范围为±23.5°。本文采用SINDA/FLUINT软件建立静止轨道卫星热分析模型，分析定向器温度场。定向器有限元热分析模型如图9所示，模型参数见表2。取图7中驱动单元 1作为研究对象，结构参数见表3。驱动单元中，层合板的铺层分别为[Ct=0.5 mm/Alt=0.5 mm]和[Alt=0.5 mm/Ct=0.5 mm]。当太阳光入射角β=23.5°时，驱动单元的温度场沿x方向分布情况如图11所示。

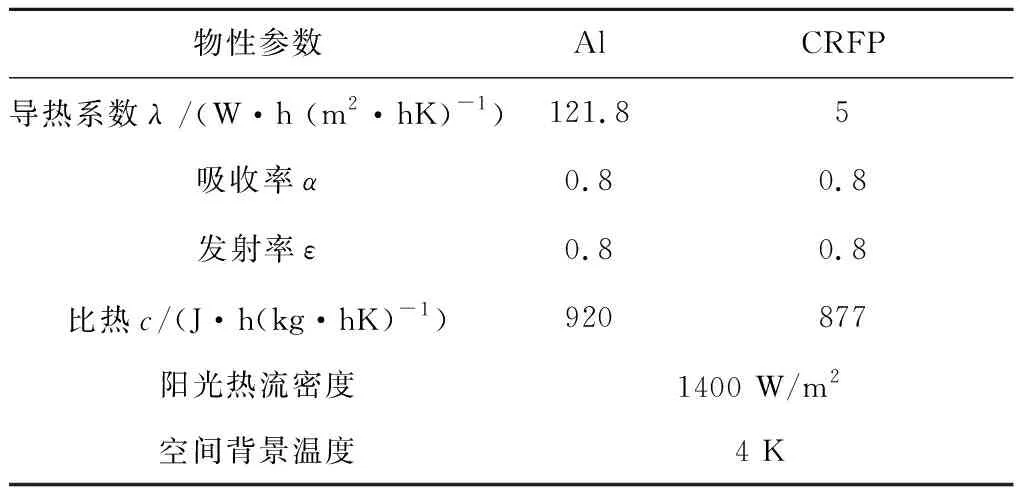
表2 模型参数Table 2 Model parameters

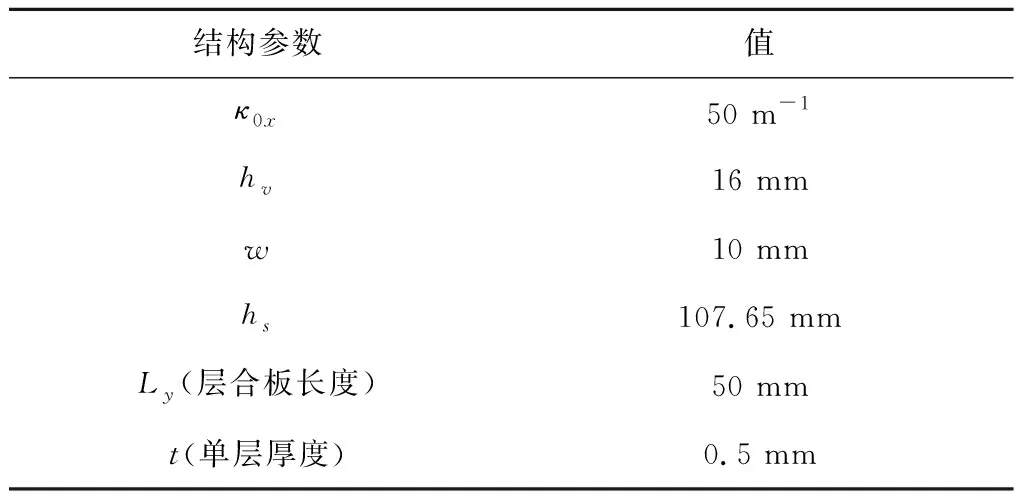
表3 驱动单元 1结构参数Table 3 Driver element 1 structure parameters

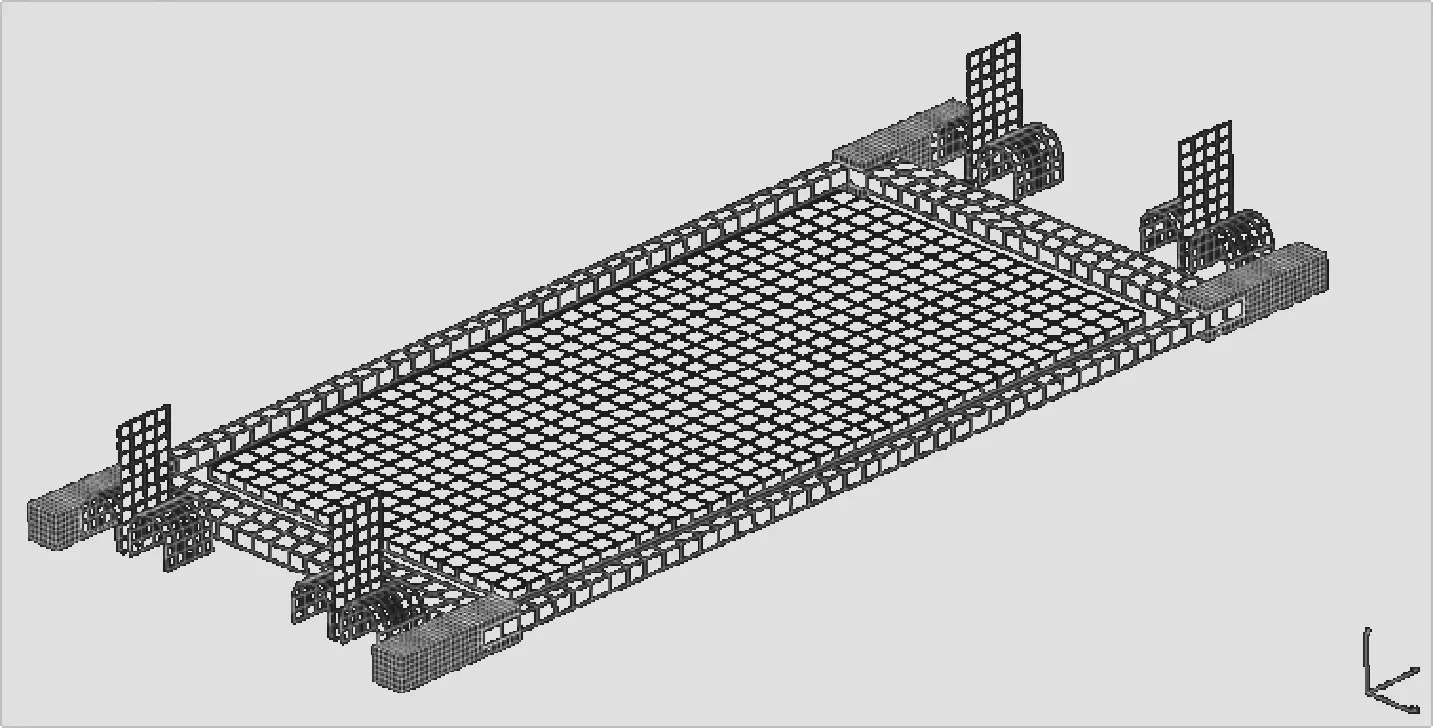
图9 定向器有限元热分析模型Fig.9 Thermal analysis FEA model of sun tracker

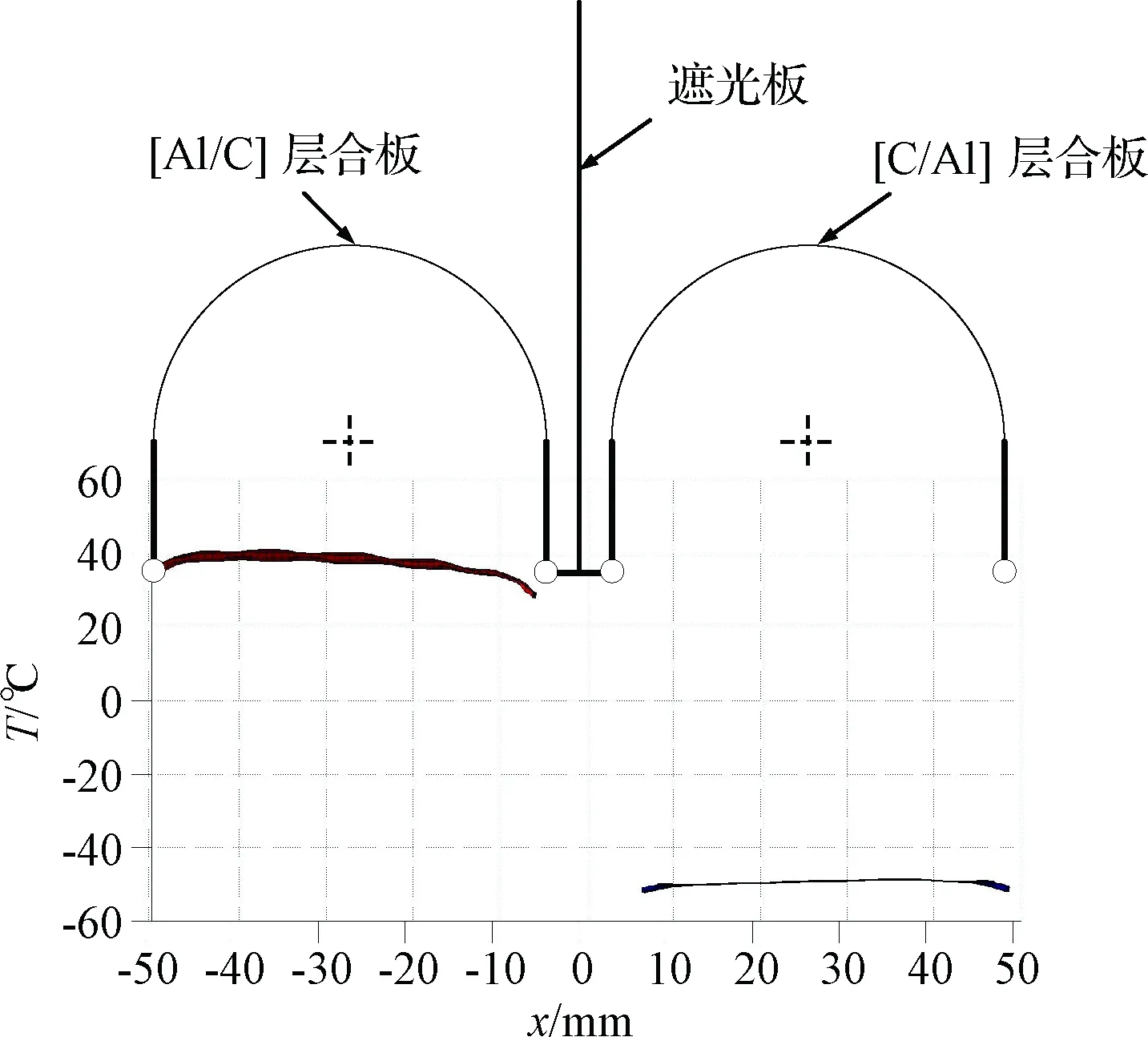
图10 驱动单元 1 [Ct=0.5 mm/Alt=0.5 mm]和[Alt=0.5 mm/Ct=0.5 mm]结构在β=23.5°时温度场沿x方向分布情况Fig.10 Temperature field distribution along the x direction of[Ct=0.5 mm/Alt=0.5 mm] and [Alt=0.5 mm/Ct=0.5 mm] structures of driver element 1 with β=23.5°

定向器复合材料层合板的平均温度T与太阳光入射角β的关系如图11所示。图11表明，[Ct=0.5 mm/Alt=0.5 mm]层合板结构和[Alt=0.5 mm/Ct=0.5 mm]层合板结构的温度在x方向及y方向的变化梯度较小。

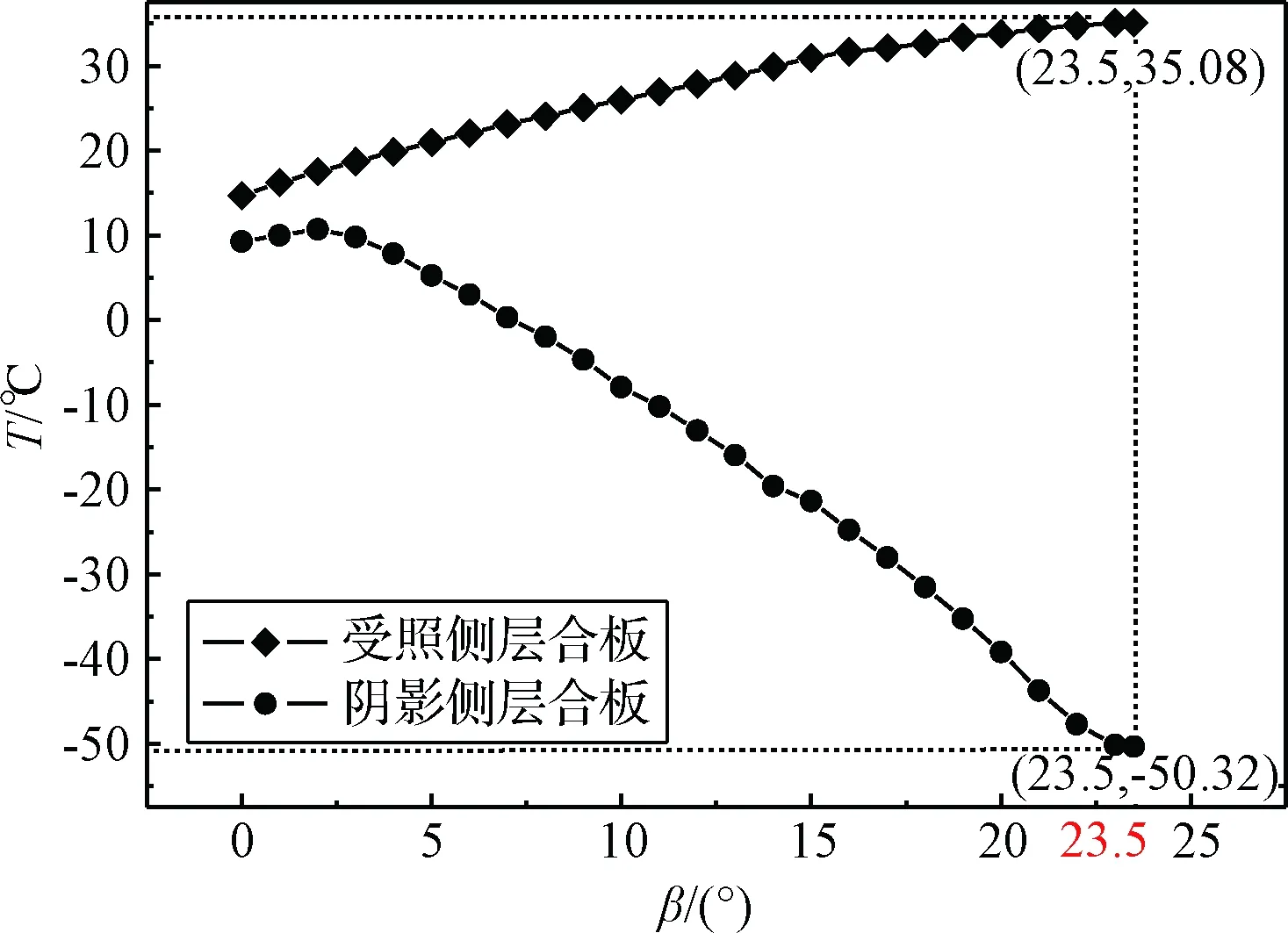
图11 定向器复合材料层合板平均温度T与入射角β关系Fig.11 The relationship between the average temperature T of the composite laminates of the sun tracker and the incident angle β

计算结果表明，受照侧[Ct=0.5 mm/Alt=0.5 mm]层合板的温度和阴影侧[Alt=0.5 mm/Ct=0.5 mm]层合板的温度随入射角基本呈线性变化。取图7中驱动单元 1作为研究对象，遮光板左侧为[Ct=0.5 mm/Alt=0.5 mm]层合板结构，遮光板右侧为[Alt=0.5 mm/Ct=0.5 mm]层合板结构。初始条件T0=20 ℃，将仿真分析得到的温度场数据作为载荷，建立驱动单元的有限元模型并分析其热变形。驱动单元 1整体结构热变形Δx与阳光入射角β的关系曲线如图13所示。计算结果表明，随阳光入射角β的增加，驱动单元 1的整体结构热变形Δx随入射角基本呈线性变化，即驱动单元 1整体驱动位移随入射角基本呈线性变化。

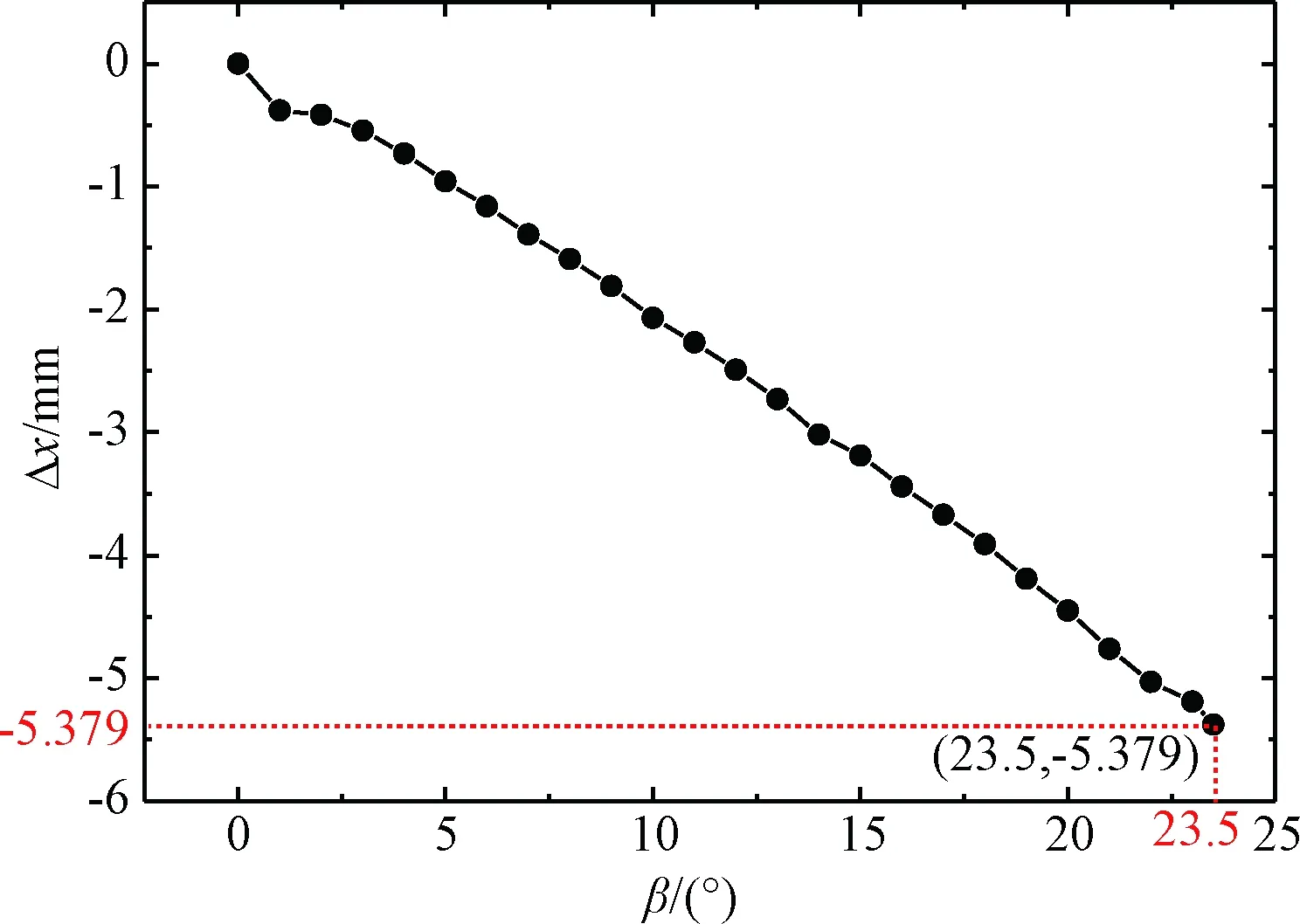
图12 驱动单元 1整体结构热变形Δx与β关系曲线Fig.12 Relationship between the thermal deformation Δx of the driver element 1 and the incident angle β

4 自适应对日定向器对日定向分析

根据图7中驱动机构的几何关系可知，定向器转角φ与驱动器的热变形Δx满足关系式：

(14)

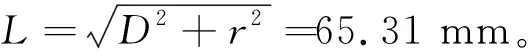
图13 定向器FEA模型Fig.13 The rotation FEA model of the adaptive sun tracker

初始温度T0=20 ℃，将图11中不同太阳光入射角对应的复合材料结构温度T作为输入载荷。通过FEA模型分析，对日定向器转角φ与太阳光入射角β的关系如图14所示。

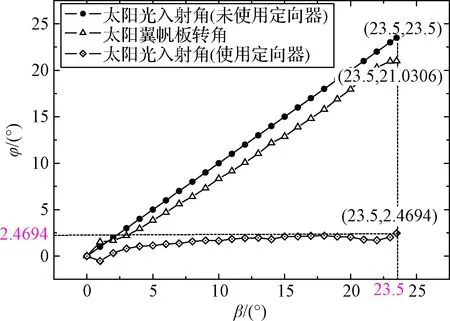
图14 定向器转角φ与太阳光入射角β的关系Fig.14 The relationship between the rotating angle φ of the sun tracker and the incident angle β of sunlight

图14分析结果显示，自适应对日定向器能明显降低了地球静止轨道中太阳光线与太阳翼法向之间的夹角β。使用自适应对日定向器后，太阳光入射角最大值为2.4694°。而定向器性能目标是太阳翼法向与太阳光夹角最大值小于±2°，因此需要优化定向器结构参数。图14表明，定向器转动角度小于理论转角。分析其原因为，在分析驱动单元 1整体结构热变形Δx时，是将其作为自由变形来考虑。然而，在整个定向器系统中，该结构不是自由变形，各结构间存在变形耦合作用，结构实际热变形小于自由状态下的热变形值小。结构热变形Δx一定时，转角φ与曲柄长r满足关系：

(15)

为了增大定向器转角，设计曲轴时，可适当减小其长度。当取曲柄r=11.50 mm时，对日定向器转角φ与太阳光入射角β的关系如图15所示。

图15表明，适当减小曲轴长度能增大定向器转角，能够有效提高自适应对日定向器对日定向精度。当r=11.50 mm时，使用自适应对日定向器后，太阳光入射角与太阳翼法向夹角在±1°范围内变化，满足定向器性能指标(太阳翼法向与太阳光夹角小于±2°)要求，对日定向精度较高。

5 结构参数分析

自适应对日定向器的驱动力矩为重要指标。驱动力矩越大，对日定向器对入射角变化作出响应越快。由于定向器转角φ与驱动单元变形Δx及曲柄长度r有关，为使转角φ保持与入射角β相等，当Δx发生变化时，r取值也将发生变化。本节主要分析自适应对日定向器的驱动单元变形量、转动机构曲柄长度以及自适应对日定向器的驱动力矩与混杂驱动复合材料层合板厚度之间的关系，即Δx-t,r-t及M-t关系。

混杂复合材料层合板中，金属层与纤维层厚度相同。本节利用有限元模型分析太阳光与太阳翼法线夹角为β=23.5°，层合板单层厚度t从0.3 mm到1.0 mm变化时的Δx-t,r-t及M-t关系。驱动单元 1整体结构参数分析结果如图16所示。

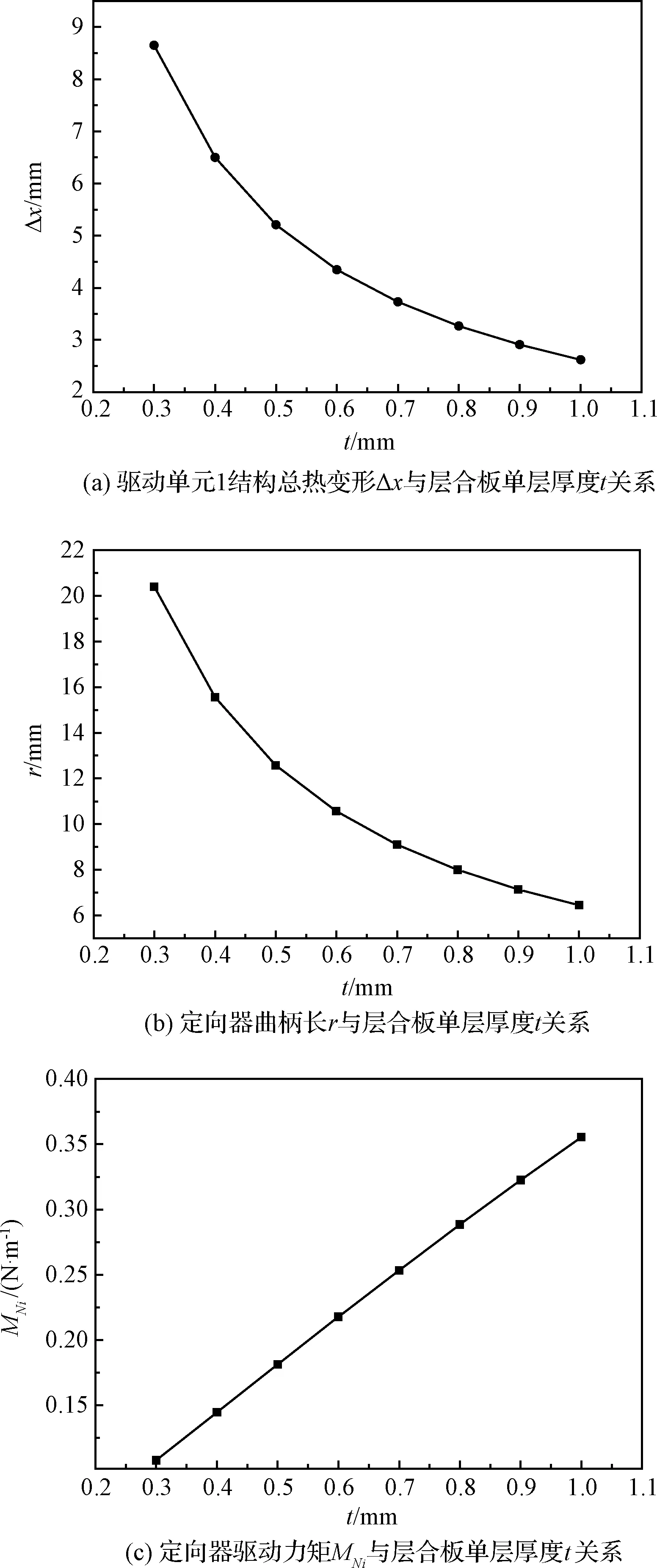
图16 驱动单元 1整体结构参数分析结果Fig.16 Parameter analysis results of the driver element 1

图16分析结果表明，驱动单元 1驱动位移Δx随层合板单层厚度t的增加而越小，曲柄长r也随层合板单层厚度t的增加而越小，但结构驱动力矩MNi随层合板单层厚度t的增加而增大。当层合板单层厚度t=0.5 mm时，驱动单元 1的驱动力矩MNi=0.1814 N·m-1，单个太阳翼的自适应定向器单元总驱动力矩MN=4×MNi=0.7256 N·m-1。由于太阳翼转轴的阻力力矩接近零，因此自适应定向器的驱动力矩满足实际工程中驱动力矩与阻力力矩之比大于1的要求。