高超声速气动加热关联方法的适应性分析

杜 涛，陈闽慷, 李凰立，张耘隆，沈 丹

(1. 北京宇航系统工程研究所,北京 100076；2. 中国运载火箭技术研究院，北京 100076)

0 引 言

飞行热环境的预测是高超飞行器设计的核心问题之一[1-2]。提升飞行热环境预测的正确性和可靠性，一方面在于发展先进的试验和测试技术、完善高精度数值模拟技术，另一方面也需要发展关联外推技术。首先风洞受原理限制，模拟条件不能复现飞行条件，试验结果不能直接用于飞行热环境的设计[3]。可以直接模拟飞行条件的数值模拟近些年来获得长足进展，但是数值方法的检验和验证还需要开展深入的工作[4]。为了克服风洞试验和数值仿真缺陷带给设计工作的风险，国内外在航天实践中发展和应用了关联外推技术，通过建立飞行环境同试验环境之间的关联关系，以实现试验和数值结果，预测飞行条件下的气动力热环境[5]，这一问题在专业上也被称为天地一致性问题[6-7]。美国在航天飞机的研制上，气动力预测采用了第三类黏性干扰关联参数关联方法[8-10]，在气动热预测中采用了St数-Re数关联方法[11]，实现了风洞试验结果外推预测飞行环境。

关联方法在飞行器设计上的重要价值，体现在：

1) 利用地面试验数据可预测飞行条件的气动力热环境；

2) 校验试验和计算数据，发现数据的缺陷和问题；

3) 指导飞行器的地面风洞试验设计。

本文将研究气动热预测的St数-Re数经典关联方法的适应性。Langley中心在猎户座成员探索飞行器(CEV)的气动开发研究中，发现St数-Re数经典关联关系不是普适的，存在风洞设备的依赖性[12]。1985年，Miller等[13]在分析双椭球锥热环境试验数据时，提出了将黏性干扰系数和激波前后的密度比引入St数-Re数经典关联关系，这一参数在后续文献中被称为Miller’Stanton数。1993年，Olivier等[14]认为Miller’Stanton数适用于类似航天飞机轨道级的钝前缘飞行器，对于锐前缘类型的滑翔飞行器，可以不考虑熵层的影响。2001年，日本NLA的Hozumi等[15]对地面试验和飞行遥测分别得到的高超试验飞行器HYFLEX的热环境数据开展了关联分析，认为黏性干扰和归一化焓差(1-hw/h0)对关联关系有重要影响。2010年，Langley中心的Hollis[12]针对层流和湍流流态，提出了在St数-Re数关联关系上引入一个激波外缘参数的修正系数β，表达形式为

式中：指数n的取值因为层流和湍流状态而不同。

2011年，李明等[16]利用黏性干扰参数、归一化焓差、驻点钝度参数等多个参数开展了国内低密度风洞和激波风洞试验数据的关联分析。

从上述发展可以看到，气动热环境关联方法研究工作始终是围绕St数-Re数关联关系展开。因此研究St数-Re数的构造机制和适应性有着重要理论价值和应用价值。在本文中，将以驻点为研究对象，从Kemp-Riddell公式出发，推导经典的斯坦顿数和雷诺数0.5次幂关系。虽然驻点并不能完全代表飞行器的分布情况，但是驻点热流关联关系存在是飞行器分布热流关联关系成立的必要条件，且推广成功是较高的。研究工作对于指导飞行器热环境关联函数的构造有着实际意义[12]。

1 雷诺数-斯坦顿数关联关系

经典的St-Re关联关系，即

St·Re0.5=C

(1)

式中：

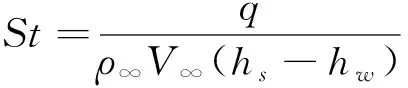
其中，q表示飞行器表面热流，ρ∞为来流密度，V∞为来流速度，hs表示驻点恢复焓，hw表示壁面焓，L表示特征尺度，μ∞表示黏性系数。C表示常数。

满足上述条件，则可构造归一化的热环境分布如下：

(2)

航天飞机轨道级的再入气动热环境设计和分析，即采用了上述关系[11]。

2 驻点雷诺数-斯坦顿数关联关系分析

驻点热流预测的Kemp-Riddell公式如下：

(3)

式中:ρc=1.225 kg/m3,Vc=7900 m/s。

文献[18]经过大量试验数据比较后认为，该公式与试验结果一致性最好，可适应1800～17100 m/s的速度范围。简化式(3)得

(4)

式中：C′=5.26051×10-8。

进一步：

(5)

于是有

(6)

式(6)揭示了经典的St-Re关联关系的影响要素，但是右边的各个参量之间不独立，需要简并。

在低焓范围内，有热力学关系

μ=0.296109×10-6h0.7259

同时，激波前后满足能量关系

激波后速度为亚声速，来流速度越高，波后速度越低，忽略波后速度，可以得到

V∞=[2000(hs-h∞)]0.5

这里焓值的单位为KJ/kg。可以验证马赫数为3和5时，该简化公式偏差分别为4.3%和3.3%。显然来流马赫数更大，偏差会更小。

则式(6)右边项可以表示为

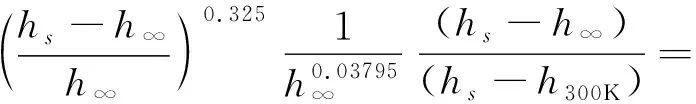
C‴·K1·K2·K3

(7)

式中：

C″=4.35×107

C‴=C′·C″=2.2865

(8)

(9)

(10)

下面分别研究K1，K2和K3三个函数的分布特性和对St和Re数之间关系的影响。

K1表征激波前后焓值之比的影响。激波前后的焓值比，有如下关系[19]

式中：θ表示激波角，对驻点附近的正激波，θ=90°。

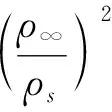
(11)

上述简化处理Ma=3时，偏差4.5%，Ma=5时，偏差3.4%，假设合理。可得：

(12)

式(12)显示K1表征了来流马赫数对关联关系的影响。

第二项K2显示了来流静焓(静温)的影响。图1给出了K2的分布情况，横坐标表示来流静温。曲线分成了三段，每一段代表不同的工况。150 K～300 K代表飞行条件。低于150 K代表常规低焓地面设备。随着地面试验技术的提升，各国陆续建成了高焓风洞设备，典型如德国宇航中心的HEG高焓激波风洞，来流静温可以达到790 K和1200 K，气流速度超过5000 m/s[20]。大于300 K区间表示高焓地面设备。从图1可以看出，在飞行条件、高焓地面设备和主要的低焓设备工作范围内，K2变化很小，随着来流静焓的增加，略微下降。总的来说，这一项值的变化是比较小的，可以选择常值替代，设定为K2=0.8。

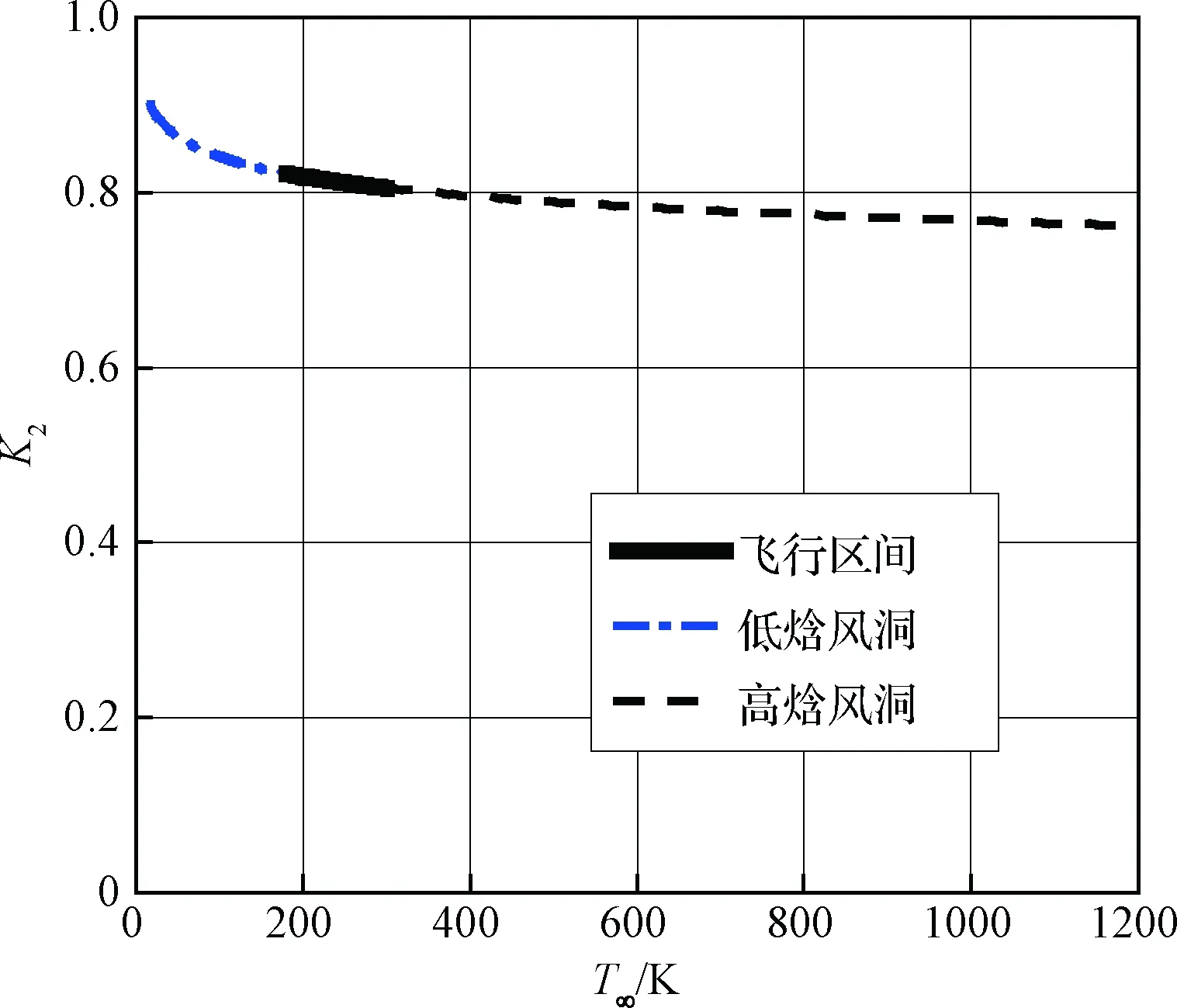
图1 K2的分布特性Fig.1 Distribution for K2

下面分析K3:

(13)

由式(13)可知,K3表征了来流静焓同来流马赫数的匹配性对关联关系的影响。K3的特性比较复杂，图2给出了五个来流静温18 K,50 K,200 K,250 K和800 K下，K3随马赫数变化的分布特性。从图2可以看出，飞行条件和高焓设备范围(来流静温200～800 K)，马赫数大于5以后，K3已经很好地逼近1，对关联特性无影响。低焓风洞范围的K3曲线表现复杂，存在一个临界马赫数Macr。临界马赫数是K3函数的一个奇异点。

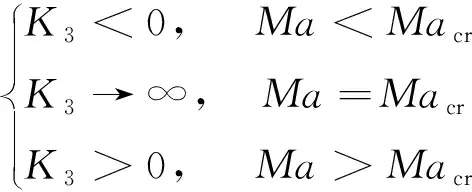
(14)

图2 K3的分布特性Fig.2 Distribution for K3

现在分析临界马赫数的意义。假定临界马赫数时，激波后的恢复焓正好为h300K，即h0=h300K，则

则式(13)为

(15)

由式(15)可知，临界马赫数的物理意义为该来流马赫数下波后的焓值h0等于参考焓值h300K。临界马赫数与来流静温T∞是对应的，可以算出临界马赫数为

(16)

图3给出了临界马赫数随来流静温变化情况。来流静温越低，临界马赫数越高。T∞=50 K的临界马赫数是5，T∞=18 K的临界马赫数为8.85。

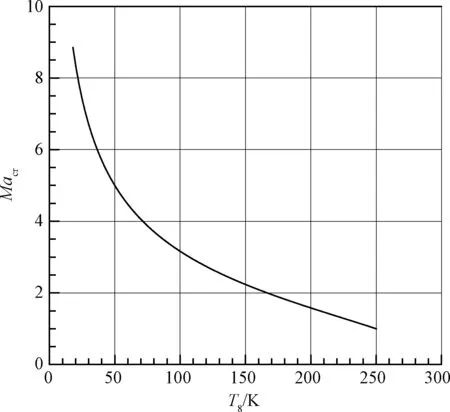
图3 临界马赫数随来流静温变化Fig.3 The critical Mach number according inflow static temperature

选择300 K作为参考焓值有现实意义，代表了试验的冷壁焓值。当风洞来流马赫数低于对应的临界马赫数，壁面热流为负，结果无意义。

风洞试验的设计点也不能选择在临界马赫数附近，这表征波后的焓值与壁面焓值接近，从测量上微小的扰动会引起较大的测量波动，更为重要的是分析显示结果不具有关联性。当马赫数跨越临界马赫数后逐步增大时，K3快速单侧逼近1。T∞=18 K曲线逼近1的速度明显慢于T∞=50 K曲线。前者在马赫数超过15以后比较良好逼近1，后者马赫9以后比较良好逼近1。T∞=50 K是目前国内的主力低焓风洞的典型工况。而来流静温越低的设备，需要提高试验马赫数才能获得与飞行条件关联度高的试验结果。

通过上述分析，可以得出如下结论：

1)为了试验结果与飞行条件具有良好的关联性，热环境风洞试验点远离临界马赫数。

2)来流静焓对于地面风洞试验设计是一个重要的参数，过低的来流静焓，需要提高试验马赫数才能获得与飞行条件具有关联的试验结果。

3)高焓试验设备是重要的，试验数据与飞行条件具有更好的关联性。

可知在关联关系中

K3=1

综合上述结果，可以得到如下表达式：

(17)

式中：C=C‴·K2·K3=1.085。可见St数和Re数经典关联关系是有限制性条件，来流马赫数和来流静焓都需要满足一定的条件。

3 Fay-Riddell公式计算的验证

采用Fay-Riddell公式计算了30 km,50 km,60 km和70 km高度上，速度在1500～8000 m/s范围内变动的驻点热流，开展关联性分析。图4采用经典的St-Re关联关系分析，坐标为对数坐标。结果无关联性。这表明经典的St-Re关联关系不具有普适性。

图5给出了按式(17)关联分析，横坐标是Re0.5/Ma0.65，纵坐标是St数。结果之间实现了关联。图中的空心符号表示马赫数低于8的工况，关联性稍微差些，原因在于马赫数较低时候，需要考虑焓差影响，即K3的影响。图中的理论直线采用了式(17)，系数C为1.185，略高于理论预测的1.085。

图4 Fay-Riddell公式预测驻点热流的St-Re数关联性分析Fig.4 St number-Re number correlation relation for stagnation point aerotheating from Fay-Riddell formula

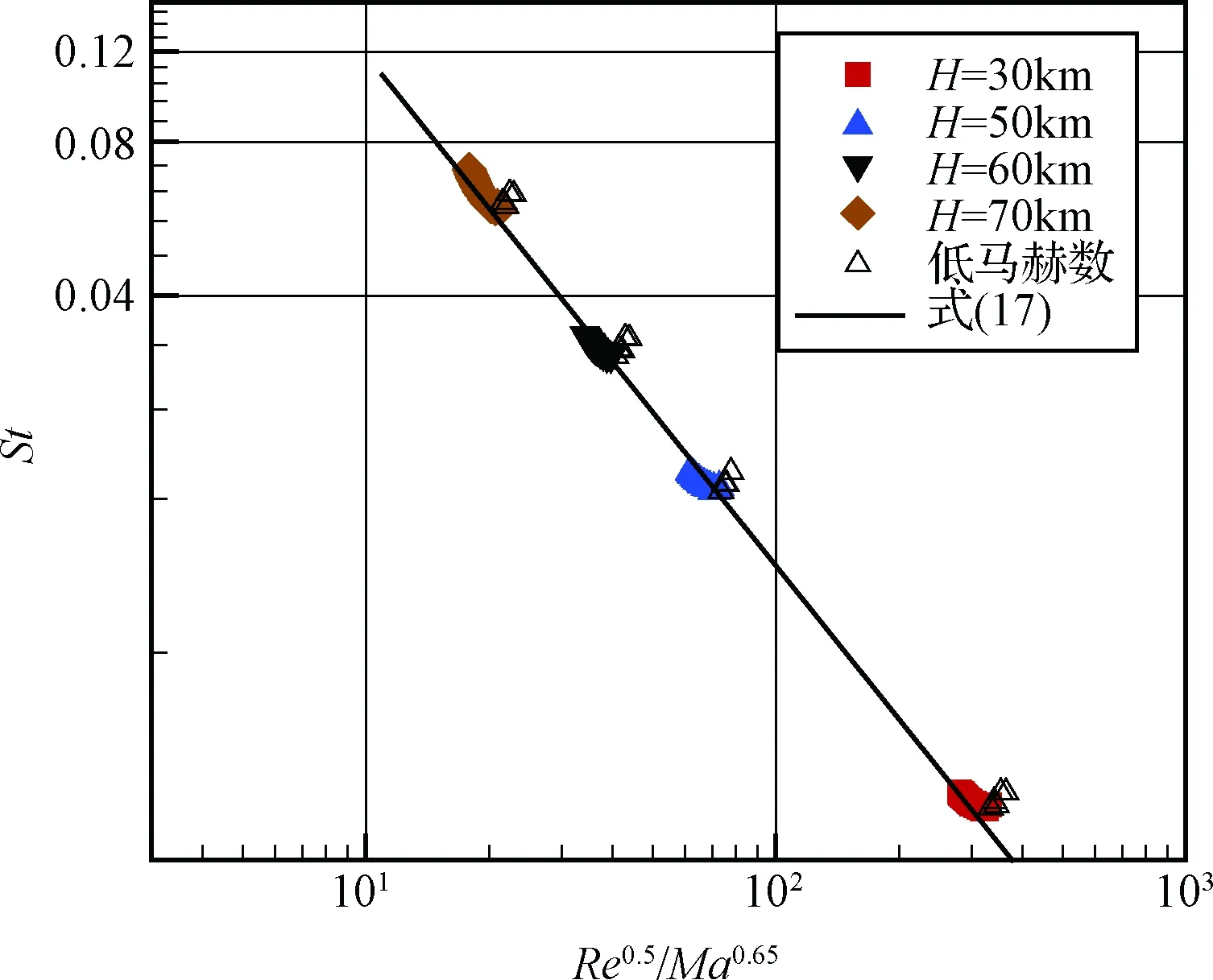
图5 Fay-Riddell公式预测的驻点热流的St-Re0.5/Ma0.65数关联性分析Fig.5 St-Re0.5/Ma0.65 correlation relation for stagnation point aerotheating from Fay-Riddell formula

4 风洞试验和数值计算的验证

为验证式(17)的正确性，开展了地面试验和数值计算。

4.1 风洞试验

在3座激波风洞和1座低密度风洞上完成了驻点热流测量试验。风洞试验状态在表1中给出。

激波风洞数据处理未按传统的相同工况取平均值作为试验结果，将单次试验结果作为独立样本参与分析，这样能够看到样本的分布特性。

Φ1 m激波风洞上的马赫数12.16工况的雷诺数最高，达到4.2×107(1/m)，且驻点半径也是最大。Φ2 m激波风洞马赫数16，雷诺数2.5×105(1/m)工况的雷诺数最低，是目前国内在激波风洞上完成的最低雷诺数工况。实现了风洞试验雷诺数跨越两个数量级，增加风洞试验代表性。

测热手段也多种多样，主要采用薄膜电阻测热。在Φ1m激波风洞上，开展了磷光热图技术测热试验[21]。Φ0.3m低密度风洞上采用红外测热方式测量热流[22]。测量手段的多样性，有助于发现和消除单一测量方式的系统性偏差。

4.2 数值计算

数值计算采用了DSMC和CFD两种计算方法。CFD方法计算了80 km和85 km两个高度状态。DSMC方法计算状况分布在85 km～94 km高空多个状态。国内多家研究机构的课题组参与了计算工作，同一状态均有多个课题组同时参与提供计算结果。以消除数值方法、格式和使用上的差异性对结果的影响。

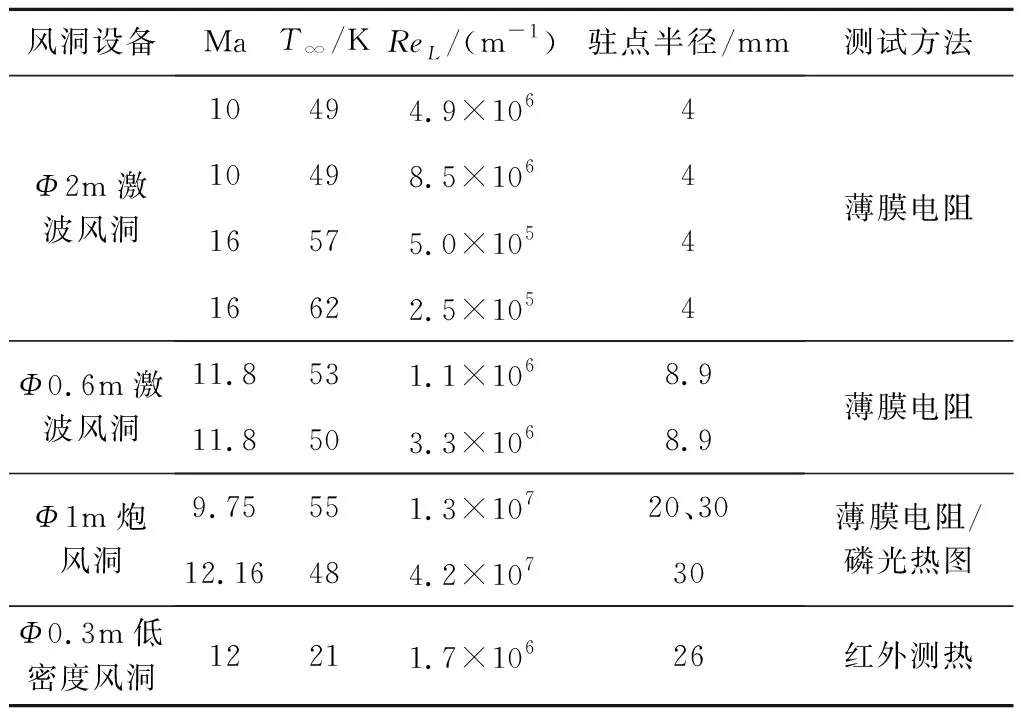
表1 风洞试验基本情况Table 1 Fundamental state for wind tunnel experiment

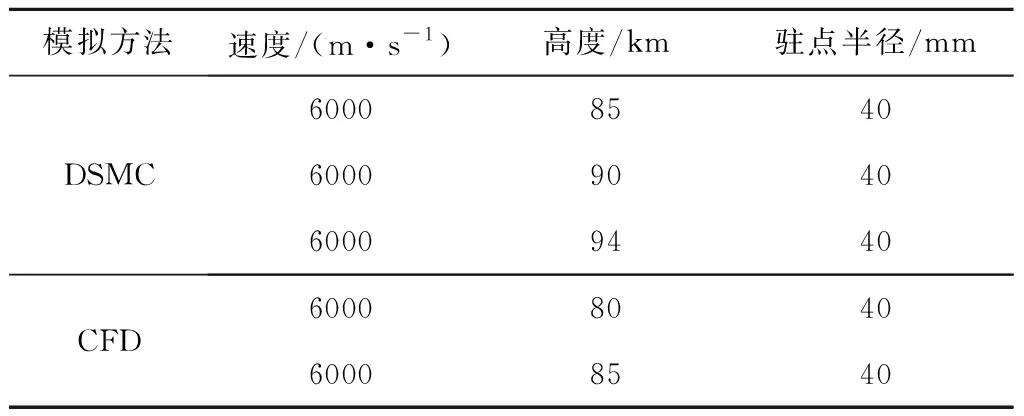
表2 数值计算状态Table 2 Fundamental state for computational simulation

4.3 工程方法计算

采用Fay-Riddell公式预测了驻点热流。计算了80 km高度以上的状态。第4.2节得到的高度70 km的不同速度的结果也参与分析。

表3 Fay-Riddell公式计算状态Table 3 Computation state for Fay-Riddell formula

4.4 结果分析

图6给出了采用经典的St-Re关联关系的分析结果。图中采用式(17)中系数，以来流马赫数12为计算点，关联系数为5.44。结果之间呈现了一定的关联性，热环境数据分布在直线附近，但关联性并不紧密，可以看出马赫数的影响。马赫数在9.75～12范围的试验结果关联最好，代表飞行状态数值仿真结果和Fay-Riddell公式预测工况，来流马赫数较高，超过20，明显偏离直线，几乎分布于理论曲线的上侧。马赫数为16的低雷诺数工况的两个试验结果也因为同样原因显著偏离关联直线。Fay-Riddell公式计算得到的高度70 km的多个马赫数结果，同第4.3节，与公式并无关联性。可见经典St-Re关联关系不具有普适性。为了验证上述结论，图7中采用马赫数22对应的系数进行关联，结果显示，代表飞行工况的数值仿真结果之间实现了良好的关联，而地面试验结果出现了偏差，均分布在直线下方。

图6 驻点热流的St-Re数关联分析(关联公式系数为5.44)Fig.6 St number-Re number correlation relation for the stagnation point aeroheating (C=5.44)

图7 驻点热流的St-Re数关联分析(关联公式系数为8.09)Fig.7 St number-Re number correlation relation for the stagnation point aeroheating (C=8.09)

图8给出了按照关联关系(17)的关联分析结果，图中横坐标是Re0.5/Ma0.65，纵坐标是St数,坐标系采用对数坐标系。常系数C同第3节采用的1.185。从图8可以看出，风洞试验和数值仿真结果之间实现了良好的关联，直线处于风洞试验结果和数值仿真结果中间，数据与数据之间的散布明显降低。另外，也可以注意到在雷诺数1.0×104～1.0×106之间，不同风洞设备获得的数据在St-Re关联分析中散布是比较大的(见图6)，而在St-Re0.5/Ma0.65关联分析中，明显散布变小(见图8)。可以得到结论：忽略马赫数效应的St-Re关联分析，适用于马赫数变化范围小的分析中；St-Re0.5/Ma0.65关联分析可以提供偏差较低的关联分析，适用于地面试验和飞行马赫数跨度范围大的关联分析和热环境预测。

DSMC获得的高度为85 km以上的飞行工况结果，既与Fay-Riddell公式给出的结果不一致，也明显偏离关联关系。因为85 km高度以上流动已经出现稀薄效应，破坏了关联关系的连续流假设基础。从图8可以看出，这个失效点大约在于雷诺数100附近。雷诺数小于100以后，需要探索新的考虑稀薄效应的关联方式。

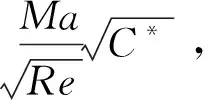
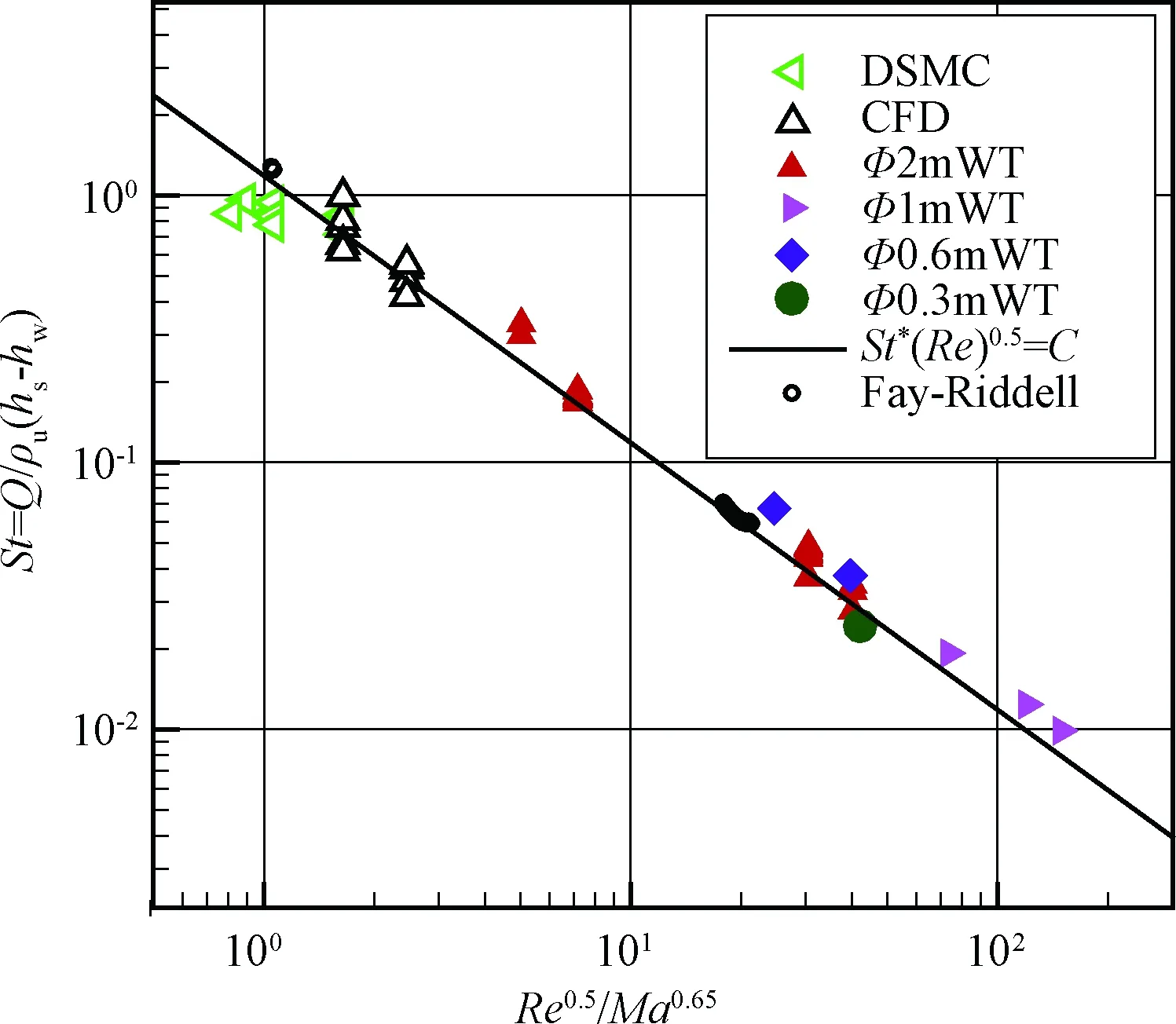
图8 驻点热流的St-Re0.5/Ma0.65数关联性分析Fig.8 St number-Re0.5/Ma0.65 correlation relation for stagnation point aerotheating

5 结 论

本文研究了热环境的经典关联方法的适应性，从Kemp-Riddell公式出发，从理论上推导了经典的雷诺数-斯坦顿数关联关系，结论显示上述关系受马赫数的制约，在马赫数变化较大的范围内，Re0.5/Ma0.65更易于实现与St数的关联。在地面风洞试验中，来流静焓值(静温)过低时，需要考虑来流静焓和来流马赫数的匹配关系，通过提高来流马赫数，抑制过低静焓对关联关系的不利影响。通过在国内4座风洞的试验结果，以及DSMC和CFD数值仿真结果，校验了结论的正确性。分析结论可以指导试验任务设计和构造全飞行器表面完整分布的关联关系。