拦截高速目标的比例与反比例导引捕获区分析
2018-10-13雷虎民
周 觐,雷虎民,侯 峰,赵 炜
(1. 空军工程大学防空反导学院,西安 710051;2. 中国人民解放军31001部队,北京 101400)
0 引 言
临近空间高超声速武器是以高超声速飞行器为载体或直接作为武器本体使用,长时间在临近空间飞行的武器,具有作战空间大、飞行速度快、突防能力强以及毁伤力大等特点,能突破几乎目前所有的防御体系,对我国空天防御安全提出了极大的挑战。所以,开展拦截此类高速目标的临近空间防御拦截弹制导控制技术研究已迫在眉睫[1-2]。
比例导引制导律其形式简单且易于弹上实现,在现役防空武器系统中得到了广泛应用[3]。在未来一段时间内,比例导引以及在其基础上发展而来的扩展比例导引,偏置比例导引等制导规律仍将作为主流制导律以应对临近空间高超声速目标威胁。因此许多专家学者开展了面向高速目标拦截作战的比例导引制导律设计。李新三等[4]基于模型静态预测规划方法设计了一种协同比例制导律,闫梁等[5-7]从普适性制导律的角度出发,设计了一种既能拦截高速目标(顺轨模式),又能拦截低速目标(逆轨模式),并同时考虑到末端碰撞角约束限制的偏置比例制导律。在其基础上,李辕等设计了针对高速目标拦截特点的三维联合比例制导律[8-9]以及偏置比例制导律[10]。白国玉等[11-12]提出了一种自动选择拦截模式并调整拦截弹速度,兼具顺、逆轨拦截能力的全向真比例制导律,仿真结果表明,该制导律可以满足对高速目标实施全向拦截的需求。秦潇等[13]考虑用扩张状态观测器对目标的机动形式进行在线估计,设计了一种带有目标机动补偿的反比例制导律。Su等[14]设计了一种考虑零控脱靶以及飞行器间安全距离的偏置比例导引律。以上研究充分考虑了高速目标拦截作战的特点,为防御作战制导律设计提供了一定借鉴,但是对于制导律初始条件的选择考虑较少。传统研究中一般都在给定的初始条件下检验所设计的制导律,如果该制导律能成功拦截目标则证明制导性能良好,如果脱靶则证明制导性能欠佳,对于初始条件设置的合理性及有效性未能给出理论证明。
针对以上问题,台湾学者Feng[15-17]和Lin等[18]研究了制导律成功拦截目标条件下拦截弹初始条件需满足的约束关系,给出了制导律的捕获区定义。Li等[19-21]沿袭其研究思路,在改进极坐标系下推导得到了制导律捕获区的相平面图(Phase portrait)。以上研究虽给出了制导律捕获区应满足的基本关系,但是推导过程特别复杂,而且从相平面图中难以有效得到拦截弹末制导初始条件设置范围。赵继广等[22]利用伴随法和蒙特卡洛打靶的方法检验了比例导引和反比例导引的捕获区,得到了二者捕获区的定性对比分析,但仍缺少理论性证明。于大腾等[23]对能量约束下的动能拦截弹逆轨拦截攻击区进行了建模,基于拦截弹和目标的机动范围在攻击区中的投影推导得到了制导捕获区与逃逸区的计算方法。Prasanna等[24]系统性地研究了比例导引与反比例导引的捕获区约束,但是其所建立的坐标系并非惯性坐标系,得出的结论并不具有普适性。
为了深入分析拦截高速目标作战过程中末制导阶段初始条件设置以及捕获区范围,本文首先结合拦截弹和目标相对运动关系,推导得到了逆轨零控拦截条件以及顺轨零控拦截条件,其次通过分析零控拦截的边界条件,建立了比例导引与反比例导引的捕获区,然后利用函数对称性,将比例导引捕获区与反比例导引捕获区在同一坐标区间下进行比较,证明了在相同条件下,反比例导引捕获区要大于比例导引捕获区,从而佐证了反比例导引在拦截高速目标作战中的优势,为应对临近空间高超声速目标威胁提供了一定的解决思路。
1 零控拦截条件分析
1.1 拦截弹和目标相对运动分析
临近空间高超声速目标速度超过马赫数5,拦截弹在末制导阶段并不具备速度优势[25],拦截弹和目标较大的相对速度造成末制导时间较短。在临近空间特殊的作战环境中,气动力的作用效果有限,拦截弹主要借助直接力或直/气复合控制[26],重力以及指令过载对速度值影响较小,因此,结合临近空间高速目标拦截作战的具体背景特点,作出如下假设条件。
假设1. 装备在拦截弹上的导引头可以是红外导引头或者雷达导引头,其最大作用距离为Rmax,忽略导引头捕获目标的过程,认为一旦弹目距离小于导引头最大作用距离,导引头即可对目标成功捕获。
假设2. 在末制导阶段,忽略目标机动影响,认为拦截弹的指令过载只改变其速度方向,忽略拦截弹和目标所受到的重力影响。
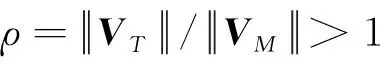
垂直平面内的拦截弹和目标相对运动关系如图1所示。
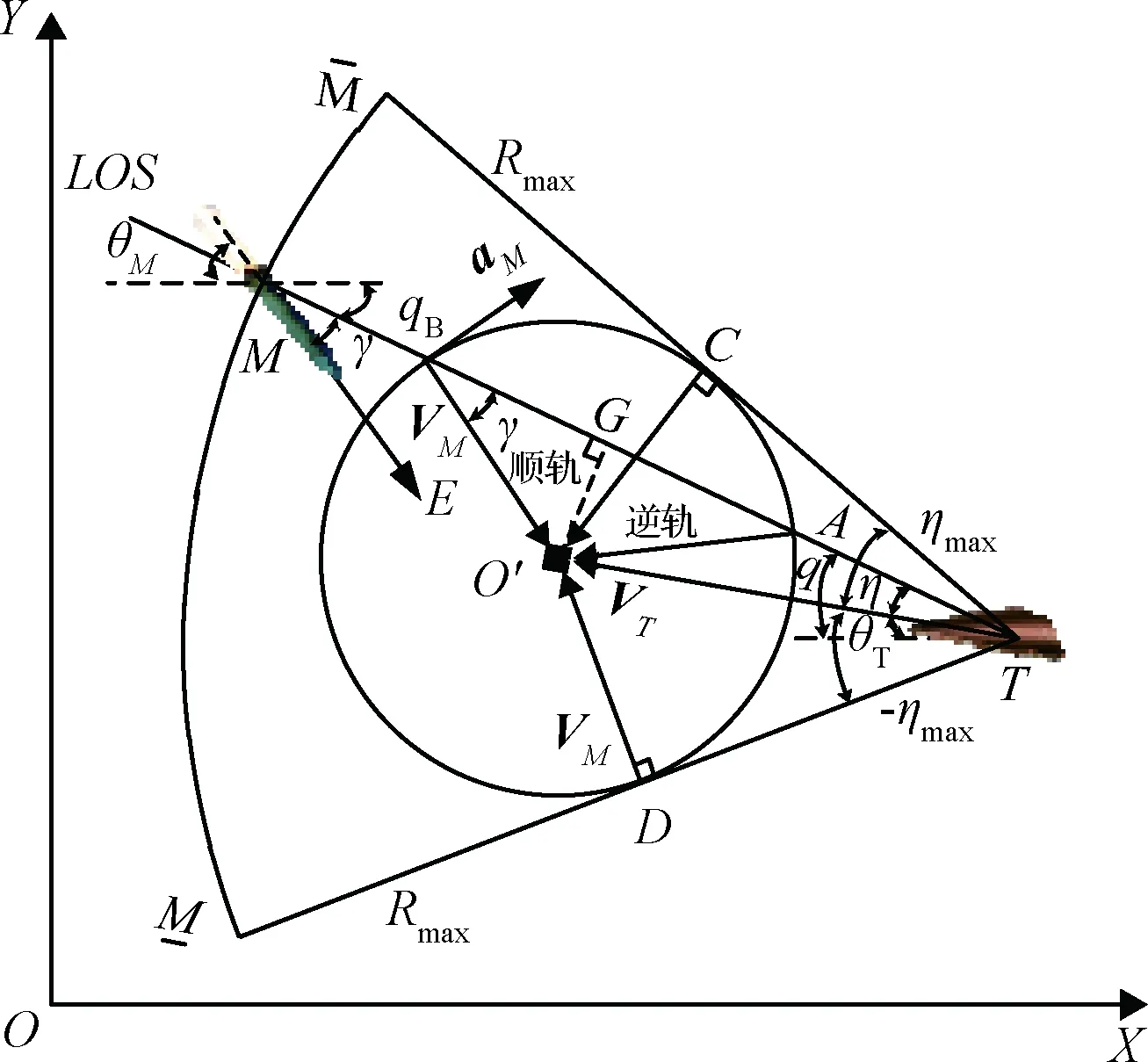
图1 拦截弹和目标相对运动关系图Fig.1 Diagram of the relative motion between the interceptor and the target
在图1中,XOY为地面惯性坐标系,M和T分别指代拦截弹和目标。M和T之间的连线为视线(Line-of-Sight,LOS),拦截弹和目标之间的距离用R表示。V和a分别表示速度矢量和加速度矢量。θ表示速度矢量V和X轴之间的夹角,即弹道倾角。q表示视线LOS与X轴之间的夹角,即视线角。从图1中可以得到拦截弹和目标的运动方程以及相对运动方程为,
(1)
(2)
(3)
γ=θM-q
(4)
(5)
(6)
(7)
η=q-θT
(8)
(9)
(10)
其中(Xi,Yi),i=M,T表示拦截弹和目标在地面坐标系中的位置,γ和η分别表示拦截弹和目标的速度矢量与视线LOS之间的夹角,即速度前置角。
1.2 顺轨和逆轨零控拦截条件分析
借鉴文献[6]中的定义,本文中将拦截弹的速度矢量与目标速度矢量之间的夹角小于π/2情形下的拦截称为逆轨(Head-on)拦截。将拦截弹的速度矢量与目标速度矢量之间的夹角大于π/2情形下的拦截称为顺轨(Head-pursuit)拦截。
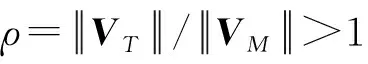
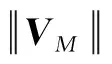
通过圆心O′作视线LOS的垂线与LOS相交于点G,那么在三角形ΔAO′B可以得到,
(11)
sinγ=ρsinη
(12)
γ=arcsin(ρsinη)
(13)
将式(11)带入到式(10)中可以得到,
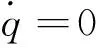
(14)
从式(12)中可以进一步求得cosγ的表达式为,
(15)
将式(15)带入到式(9)中并进行化简可以得到,
(16)
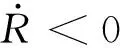
(17)
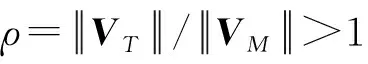
从图1中可以进一步观察发现,零控拦截条件的边界为视线LOS与拦截弹的速度矢量圆相切的情形,将切点分别记为点C和点D,此时可以得到,
γ=±π/2
(18)
将式(18)代入到式(13)中可以得到,
ηmax=arcsin(1/ρ)
(19)
从而可以得到存在零控拦截条件情况下的目标速度前置角η的取值范围是
-ηmax≤η≤ηmax
(20)
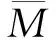
2 比例与反比例导引捕获区分析
2.1 比例导引捕获区分析
当末制导初始时刻,拦截弹和目标的速度前置角不满足零控拦截条件时,应引入末制导律将拦截弹导引到零控拦截曲线附近,确保对目标的成功拦截。
比例导引的加速度指令表达式为,
(21)
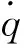
(22)
对式(8)进行求导,并将式(22)带入,可以得到,
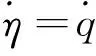
(23)
对式(4)进行求导,并将式(23)和式(3)带入可以得到,

(24)
对于式(24)等号两边进行积分,
(25)
其中,η0和γ0分别为末制导初始时刻η和γ的初值。通过观察式(25)可以发现,无论目标和拦截弹的速度比ρ取何值,应用比例导引得到的拦截弹与目标的速度前置角在(γ,η)平面内都表现为一条斜率为1/(N-1)的直线。
定理2. 在忽略目标机动影响,认为目标与拦截弹的速度比ρ保持不变的情况下,应用比例导引得到的捕获区(Capture Region,CR)在(γ,η)平面内可以表示为,
CR=(A1∩B1)∪(A2∩B2)
(26)
其中,
(27)
(28)
(29)
(30)
f(γ,η)=η-arcsin(sinγ/ρ)
(31)
(32)
(33)
(34)
(35)
(36)
(37)
证. 令式(31)中f(γ,η)=0即可得到零控拦截条件。如果目标和拦截弹的初始速度前置角η0和γ0不满足零控拦截条件,那么在末制导律的作用下,二者将逐渐收敛至零控拦截状态,以确保对目标的成功拦截。结合以上分析,在(γ,η)平面内目标和拦截弹的速度前置角将表现为一条斜率为1/(N-1)的直线,所以捕获区的边界条件应为此直线与零控拦截曲线相切的情形。因此令式(13)对γ进行求导,可以得到,
(38)
将式(38)与式(25)相比较,可以求解得到,
(39)
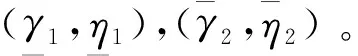
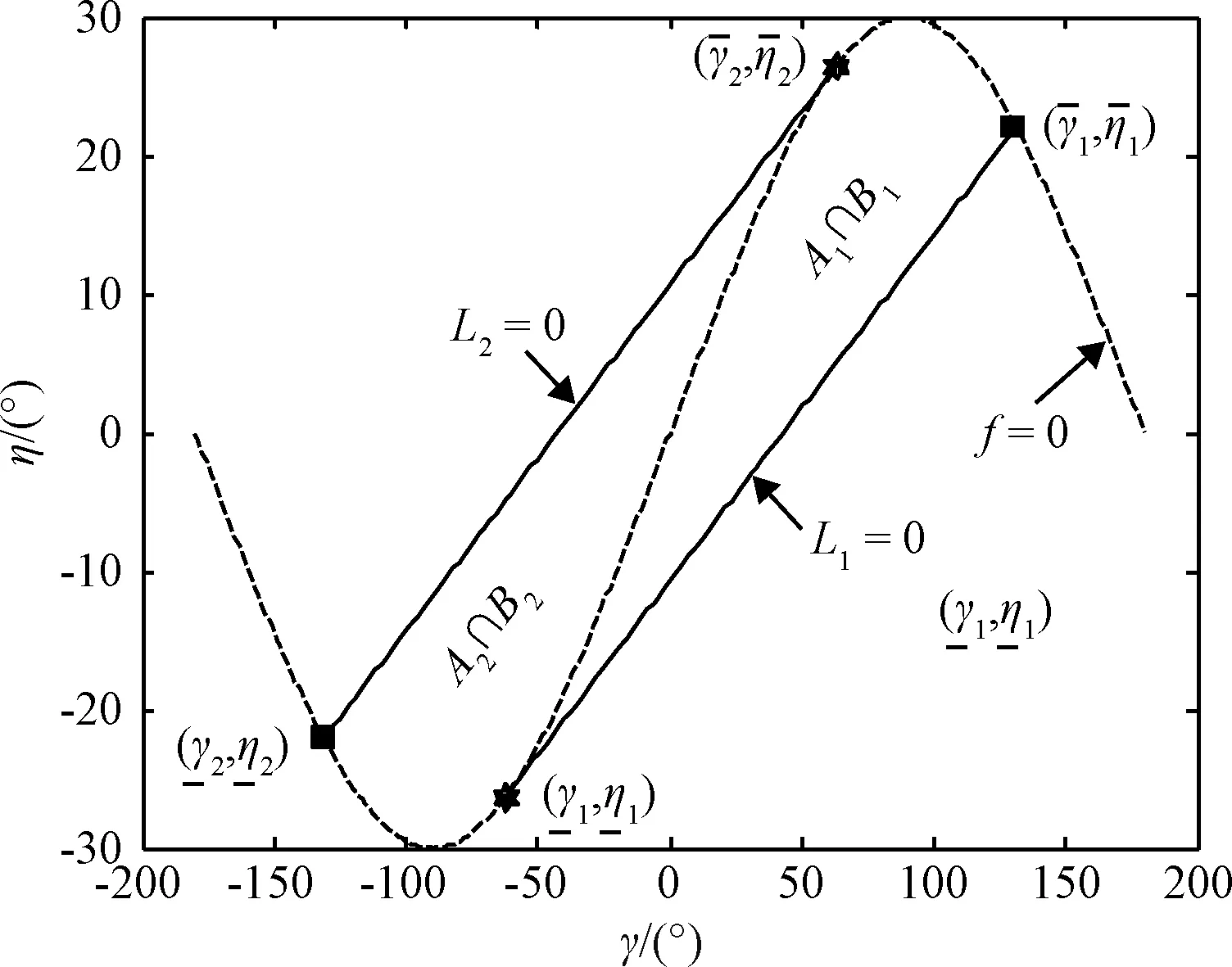
图2 N=5, ρ=2时比例导引捕获区Fig.2 CR of proportional navigation with N=5, ρ=2
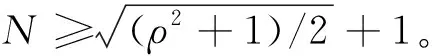
证. 根据式(39),可以得到,
(40)
结合目标与拦截弹的速度比ρ>1,可以得到式(40)中导航比N需要满足,
(41)
通过以上分析可知,拦截方可以利用定理3设置有效的导航比N,确保定理2中捕获区非空,然后根据定理2进一步解算捕获区的边界条件,得到特定导航比N以及速度比ρ情形下的比例导引捕获区范围。通过调整末制导初始时刻拦截弹状态,使其位于此范围内,从而确保对目标的成功拦截。
2.2 反比例导引捕获区分析
反比例导引的导航比为负数,其加速度指令表达式为,
(42)
所以用-N代替2.1节分析中的N可以得到反比例导引捕获区。
定理4. 在忽略目标机动影响,认为目标与拦截弹的速度比ρ保持不变的情况下,应用反比例导引得到的CR在(γ,η)平面内可以表示为,
CR=(A3∩B3)∪(A4∩B4)
(43)
其中,
(44)
(45)
(46)
(47)
(48)
(49)
(50)
(51)
(52)
(53)
定理4. 的证明与定理2的证明过程相似,在此不再赘述。图3给出了导航比N=5,目标与拦截弹的速度比ρ=2时反比例导引的捕获区。
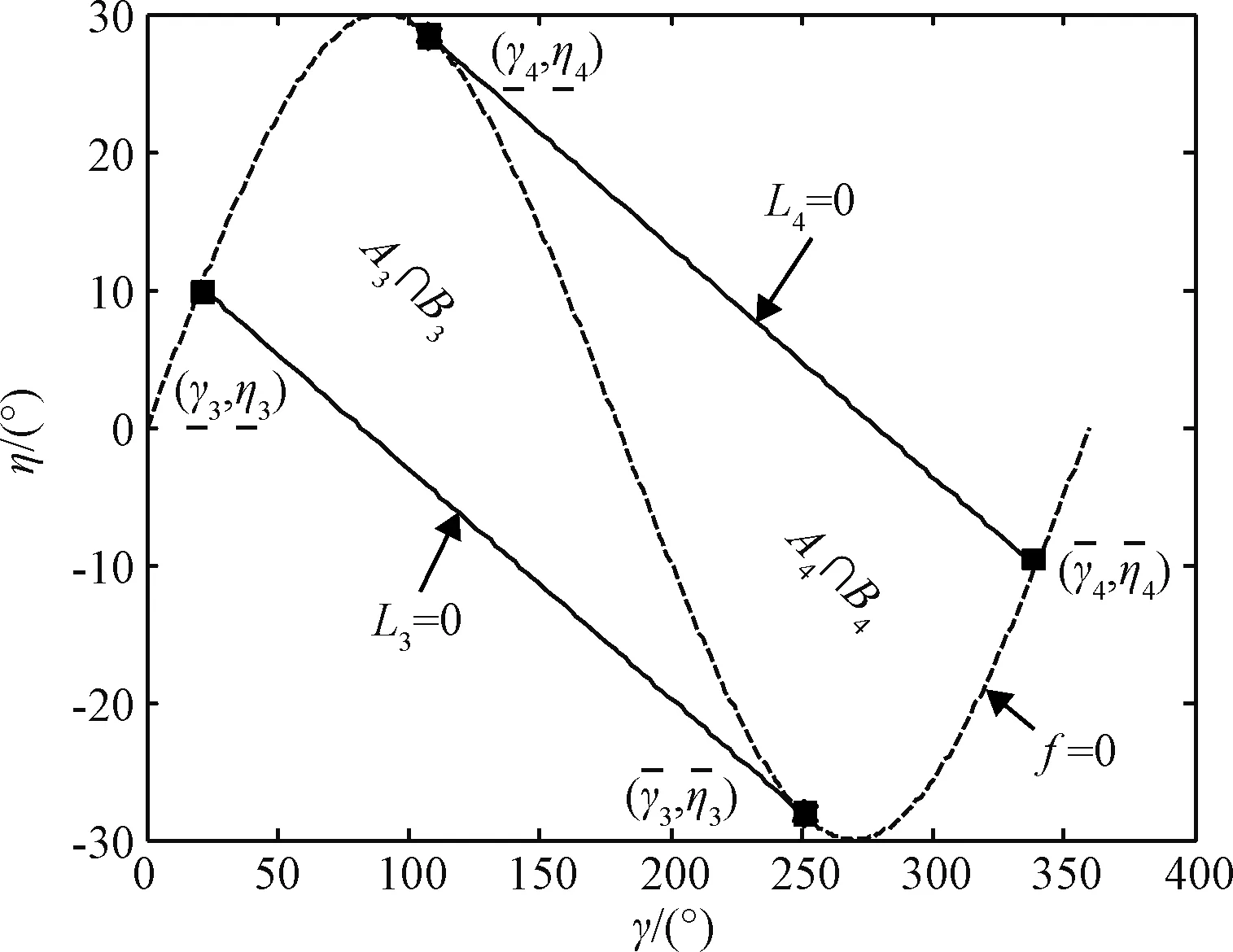
图3 N=5, ρ=2时反比例导引捕获区Fig.3 CR of retro-proportional navigation with N=5, ρ=2
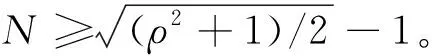
证. 根据式(50)和式(51),可以得到,
(54)
结合目标与拦截弹的速度比ρ>1,可以得到式(54)中导航比N需要满足,
(55)
2.3 比例与反比例导引捕获区对比
同一坐标系中,导航比N=5,目标与拦截弹的速度比ρ=2时比例导引与反比例导引捕获区如所图4示。
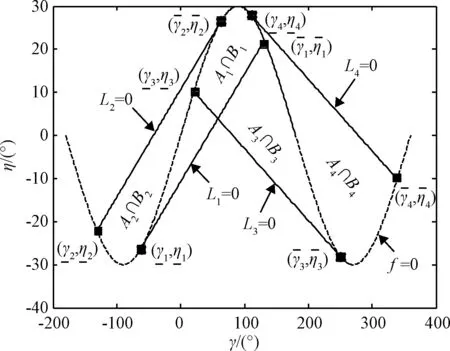
图4 N=5, ρ=2时比例导引与反比例导引捕获区Fig.4 CRs of proportional navigation and retro-proportional navigation with N=5, ρ=2
定理6. 在忽略目标机动影响,认为目标与拦截弹的速度比ρ>1保持不变的情况下,导航比为-N的反比例导引律相比于导航比为N的比例导引律捕获区要大。
证. 将零控拦截条件式(13)进行变形,记函数g(γ)为
(56)
由于g(π/2-γ)=g(π/2+γ),函数g(γ)关于x=π/2轴对称,所以将反比例导引的捕获区关于x=π/2轴旋转,得到如图5所示捕获区对比图。
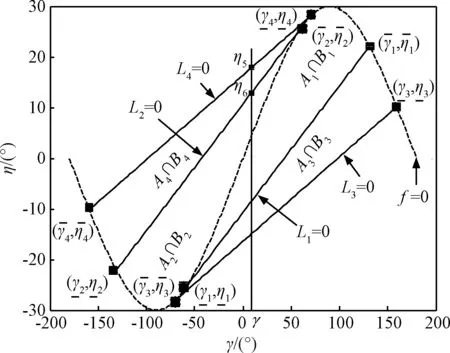
图5 N=5, ρ=2时比例导引与旋转后反比例导引捕获区Fig.5 CR of proportional navigation and rotated CR of retro-proportional navigation with N=5, ρ=2
由于g(γ)=-g(-γ),函数g(γ)关于原点(0,0)对称,因此比例导引和反比例导引的捕获区同样关于原点(0,0)对称。接下来只需要分析各自捕获区的一半。记比例导引的系数mP=N-1,关于x=π/2轴旋转后反比例导引的等效系数为mR=N+2,那么根据式(39)可以得到,切点的统一表达形式为
(57)
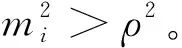
(58)
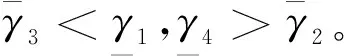
切线与零控拦截曲线的交点满足的表达式为
(59)
将函数(59)对mi求偏导可以得到,
(60)
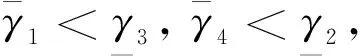
另外对于任意γ,带入到比例导引捕获区直线边界L2和反比例导引捕获区直线边界L4可以得到,
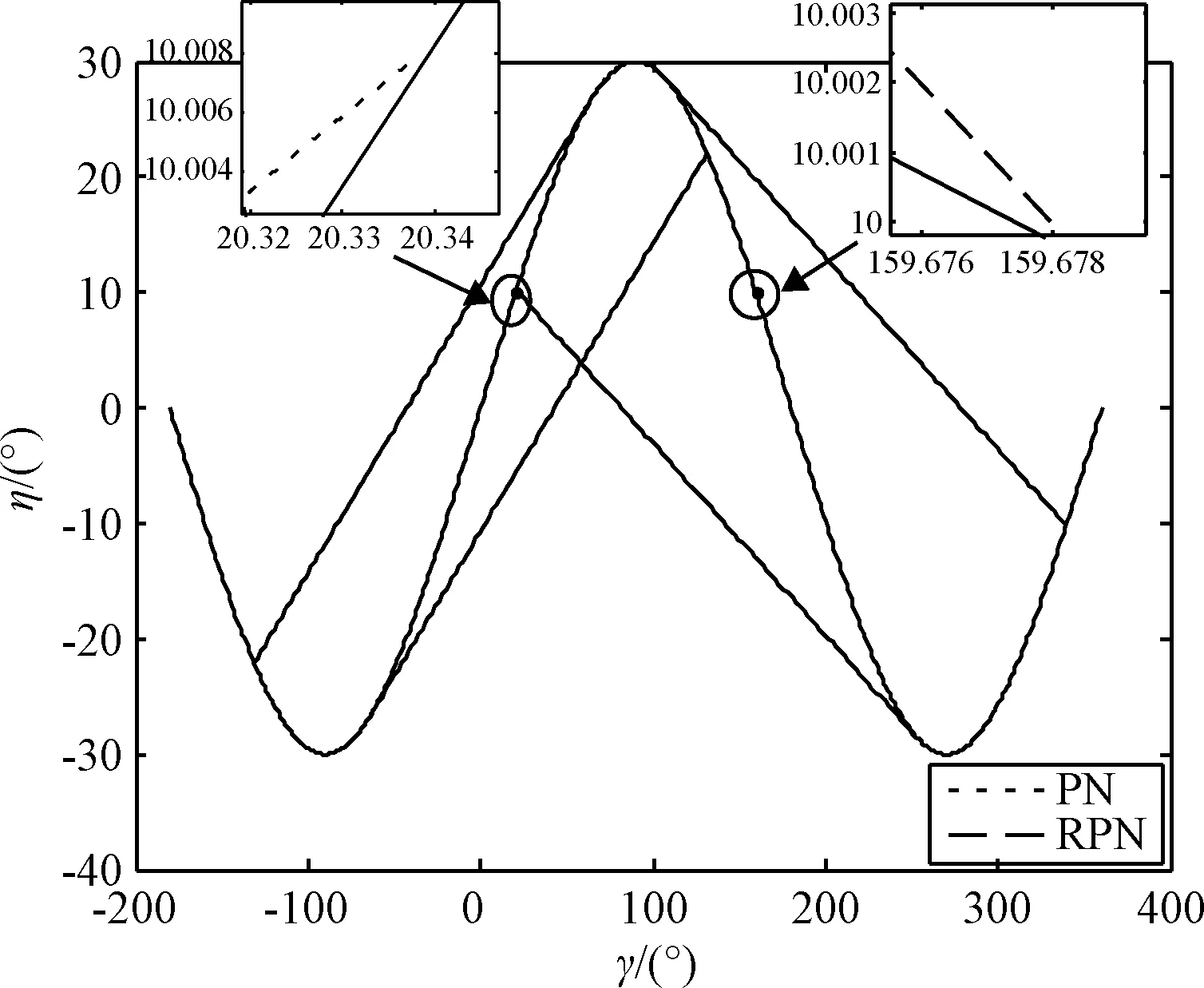
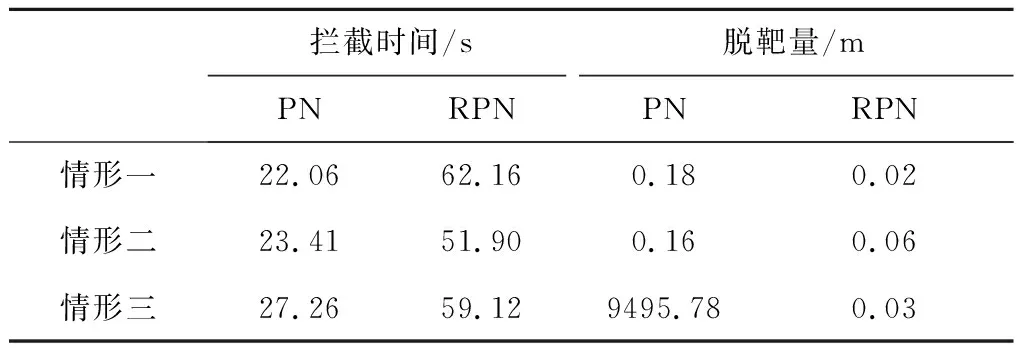
η6=L2(γ) (61) 综上所述,在忽略目标机动影响,认为目标与拦截弹的速度比ρ>1保持不变的情况下,导航比为-N的反比例导引律相比于导航比为N的比例导引律来说,其捕获区对应的区间更大,因此捕获区更大。 为验证本文对于比例导引和反比例导引捕获区理论分析的合理性,开展以下四种情形的仿真。仿真中设定拦截弹的弹上导引头最大作用距离为Rmax=100 km,忽略拦截弹过载指令延迟环节。拦截弹和目标的初始参数设置如表1所示。 表1 拦截弹和目标初始参数设置Table 1 Parameter settings of the interceptor and the target 从表1中可以发现,目标和拦截弹的初始距离满足拦截弹弹上导引头的最大作用范围约束,可以顺利进入末制导阶段。设置末制导过程中比例导引系数为5,反比例导引系数为-5。设置目标速度为3113 m/s,拦截弹速度为1556.5 m/s,目标和拦截弹的速度比为ρ=3113/1556.5=2。拦截弹的弹道倾角在四种仿真情形中发生变化,目标的弹道倾角为-180度保持不变。为体现代表性并不失一般性,此处选取目标和拦截弹的初始视线角为-10度,以尽量贴合临近空间防御作战中拦截弹再入打击的特点。 仿真情形一的设置主要是为了检验顺轨和逆轨零控拦截条件的有效性。由表1中拦截弹和目标的初始参数设置可以计算得到,目标的速度前置角为10度,结合式(13),满足顺轨零控拦截条件的拦截弹速度前置角为160度,满足逆轨零控拦截条件的拦截弹速度前置角为20度,进一步计算可以得到拦截弹的弹道倾角初始值应分别设置为-170度以及-30度。仿真得到的比例导引(PN)和反比例导引(RPN)结果如图6所示,末制导时间和脱靶量对比如表2所示。 图6 情形一捕获区曲线Fig.6 Curves of the CR in scenario one 表2 拦截时间和脱靶量对比Table 2 Comparisons of the interception time and miss distance 从图6中的捕获区曲线可以发现,目标和拦截弹速度前置角的初始条件设置满足零控拦截条件,并且在整个末制导过程中,目标和拦截弹的速度前置角都保持在零控拦截曲线附近,从而证明了本文零控拦截条件的合理性。从表2给出的末制导时间和脱靶量对比可以发现,PN和RPN都能够成功拦截目标,PN的拦截时间22.06 s要小于RPN的拦截时间62.16 s,而PN脱靶量0.18 m略大于RPN的脱靶量0.02 m。 当拦截弹的速度前置角不满足零控拦截条件时,只要其位于捕获区内,在末制导阶段就可以通过末制导律的作用将其收敛至零控拦截曲线附近。仿真情形二的设置主要考虑拦截弹的初始速度前置角不满足零控拦截条件,但仍位于比例导引和反比例导引的捕获区内。设置拦截弹的初始速度前置角为70度,仿真结果如图7所示。 图7 情形二捕获区曲线Fig.7 Curves of the CR in scenario two 图7给出了情形二中的捕获区曲线,从图中可以发现,拦截弹和目标的初始速度前置角并不满足零控拦截条件,但是仍位于捕获区内,PN和RPN分别导引拦截弹至零控拦截曲线附近,确保了对目标的成功拦截。目标和拦截弹的速度前置角在(γ,η)平面内表现为一条斜率为1/(N-1)的直线。从表2中可以发现,PN导引拦截弹选择了近点拦截,拦截时间为23.41 s,脱靶量为0.16 m,而RPN导引拦截弹选择了远点拦截,拦截时间为51.90 s,脱靶量为0.06 m。 仿真情形一和仿真情形二验证了零控拦截条件的有效性,在仿真情形三中,设置拦截弹的速度前置角为110度,使其不满足PN捕获区限制,然而仍然满足RPN捕获区限制。仿真结果如图8所示。 图8 情形三捕获区曲线Fig.8 Curves of the CR in scenario three 从表2中可以发现,PN导引最终导致了拦截弹的脱靶,脱靶量为9495.78 m,拦截时间为27.26 s,而RPN导引能够成功拦截目标,脱靶量为0.03 m,拦截时间为59.12 s。图8中给出了情形三中的捕获区曲线,从中可以发现,拦截弹和目标的初始速度前置角位于RPN导引捕获区内,RPN导引能够有效将拦截弹改变到零控拦截条件附近,确保对目标的成功拦截。由于初始条件位于PN导引捕获区外,所以PN导引不能有效引导拦截弹,从而导致脱靶。仿真情形三说明了如果拦截弹和目标在末制导阶段的初始条件位于末制导律的捕获区外,那么单纯依靠末制导去修正不良的初始条件难以满足拦截需求,必须在中制导段提前修正,以确保较好的中末制导交接班状态,为末制导提供良好的初始条件。仿真情形三在一定程度上说明了,在拦截高速目标作战场景中,RPN相对于PN具有一定的优势,在相同初始条件下,能够拦截一些传统PN制导律难以拦截的目标。 在仿真情形四中,设置拦截弹的速度前置角从0度至360度每间隔5度进行遍历,分别利用PN和RPN作为末制导律进行蒙特卡洛打靶仿真,统计成功拦截目标的情形,仿真结果如图9所示。 图9 情形四捕获区曲线Fig.9 Curves of the CR in scenario four 图9中给出了情形四中的捕获区曲线,针对同一目标,应用RPN作为末制导律的拦截弹初始速度前置角范围可以设置为[20,215]度,而应用PN作为末制导律的拦截弹初始速度前置角范围为[0,80]度。根据捕获区边界式(32)-(37)和(48)-(53)计算得到PN的捕获区范围为[-2.82,82.82]度,RPN的捕获区范围为[21.61,218.39]度。从图9中可以发现,蒙特卡洛仿真得到的捕获区曲线基本填充满了理论计算的捕获区,与理论分析完全吻合,从而证明了捕获区边界约束的有效性。 1)在末制导段拦截弹和目标相对运动过程中存在零控拦截条件,如果拦截弹状态满足此条件,那么可以在不施加任何制导控制指令的条件下成功拦截非机动目标。 2)零控拦截条件具体可以分为顺轨零控拦截条件和逆轨零控拦截条件,此条件由拦截弹与目标的速度比以及二者的速度前置角决定。 3)在(γ,η)平面内,比例导引的捕获区由逆轨零控拦截曲线以及两条与其相切且斜率为1/(N-1)的直线构成。反比例导引的捕获区由顺轨零控拦截曲线以及两条与其相切且斜率为-1/(N+1)的直线构成。 4)比例导引和反比例导引都存在各自的捕获区约束,如果拦截弹与目标初始条件不满足零控拦截条件,并且位于捕获区约束范围内,那么依靠比例导引和反比例导引可以控制拦截弹分别收敛至逆轨零控曲线和顺轨零控曲线附近,确保对目标的成功拦截。 5)针对高速目标拦截的相同作战条件下,反比例导引的捕获区要大于比例导引的捕获区。如果不考虑拦截时间影响,应用反比例导引的制导效果要优于比例导引制导效果。3 仿真校验
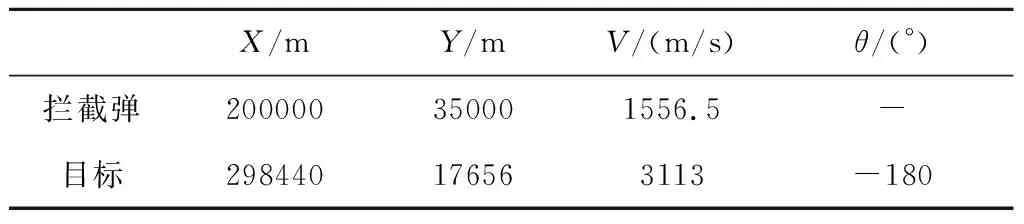
3.1 情形一
3.2 情形二
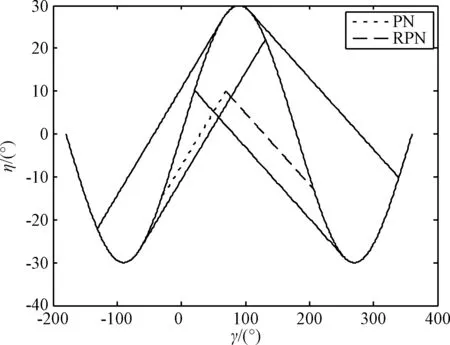
3.3 情形三
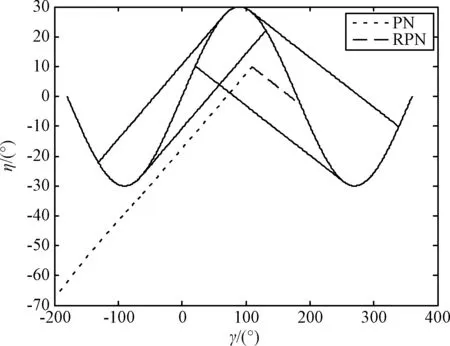
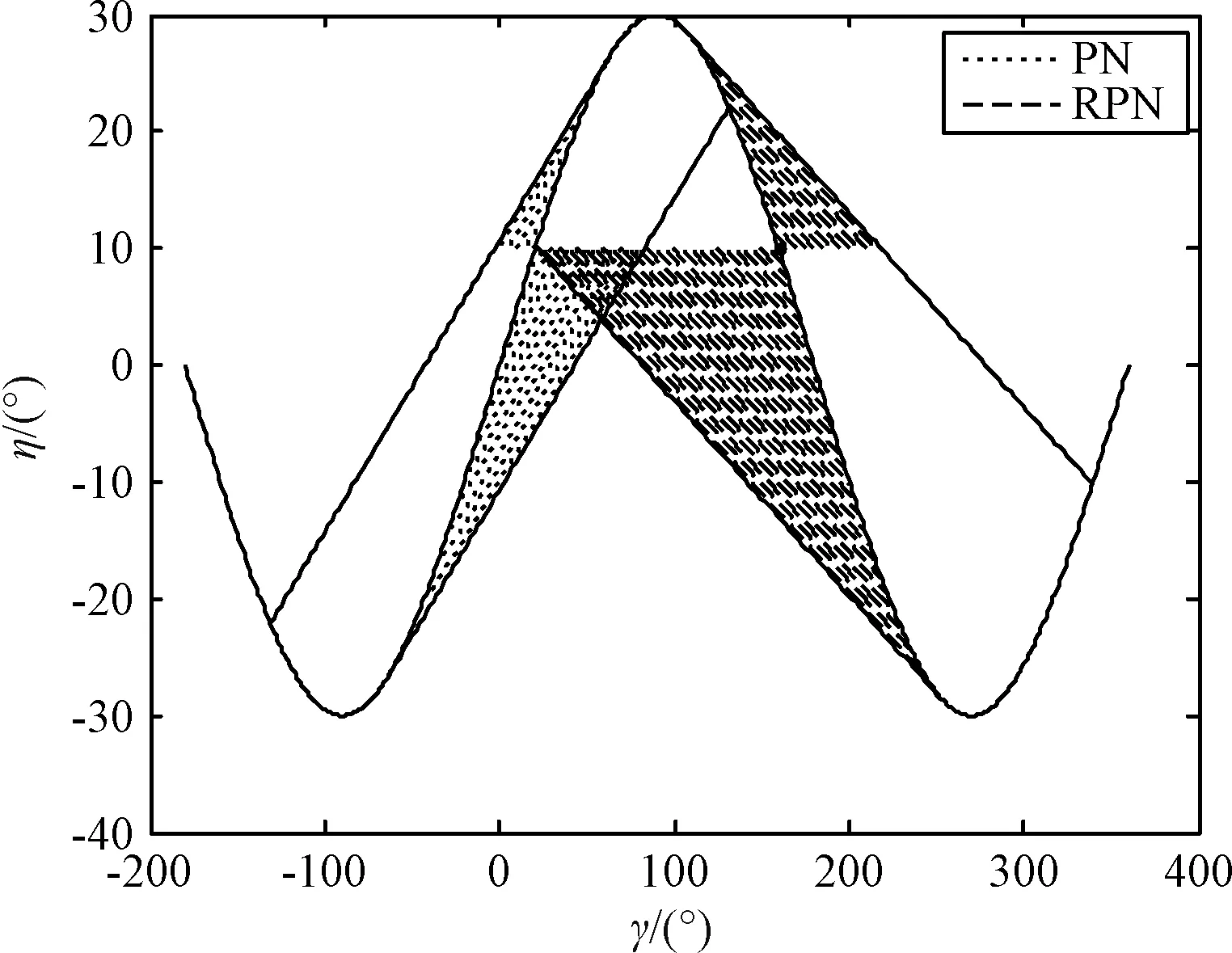
3.4 情形四
4 结 论
