基于脉冲子结构的探测器结构动力学优化设计

陈树霖，刘 莉，陈昭岳，岳振江，孙浩然

(北京理工大学宇航学院，飞行器动力学与控制教育部重点实验室，北京 100081)

0 引 言

随着航天技术的发展，工业部门对航天器性能要求不断提高，航天器结构设计逐渐由传统的先分析后校核步入优化设计阶段。航天器结构的柔性化、轻量化使得其承受的动力学环境越来越复杂，有必要在结构优化设计中将结构动力学特性分析考虑其中[1]；逐步将航天器结构设计由固有频率设计向动态响应设计过渡[2]。

考虑航天器柔性的动力学模型主要有基于多体动力学的刚柔耦合模型[3-4]，基于连续介质力学的非线性有限元模型[5-6]。肖岩等[7]建立了卫星的刚柔耦合动力学模型，在卫星姿态控制中考虑了附件柔性的影响。刘汉武等[8]建立了航天器柔性多体动力学模型并开展航天器的分离动力学分析及分离参数优化，结果表明结构柔性对航天器动力学分析不可忽视。刚柔耦合模型虽能在一定程度上反映结构柔性，但结果精度往往与模态基选取密切相关[9]；非线性有限元模型对结构的局部振动表达更加精确[10]。但非线性有限元模型自由度数较多，求解耗时，很难在结构优化中直接使用，可采用子结构方法或近似模型的方法对原模型进行简化处理以提高动力学求解效率。

脉冲子结构方法(Impulse Based substructuring Method，IBS)是一种高效求解且不损失精度的动态时域子结构方法[6]。Rixen[11]于2010年首次提出了它的标准形式。之后，董威利等[6]将该方法成功应用于月球探测器着陆阶段动力学分析中，并对标准脉冲子结构方法的连接形式进行拓展[12]。将脉冲子结构方法应用于复杂结构的优化设计中既能保证动力学响应求解精度又能有效缩短计算耗时，但脉冲响应函数的获取较为耗时，在优化过程中需要反复修改的优化区域并不适宜建成脉冲子结构。Van Der Valk等[13]进一步研究了脉冲子结构与有限元的刚性连接情况。Chen等[14]发展了脉冲子结构与有限元及模态子结构间的复杂连接情况。脉冲子结构与有限元的复杂连接的研究，为该方法在结构动力学优化设计中的应用提供了基础。

本文基于脉冲子结构方法，提出了一种考虑结构动力学响应的优化流程，建立月球探测器中心体脉冲子结构模型及太阳翼有限元模型，考虑探测器着陆段动力学过程，对探测器太阳翼复合材料铺层厚度、太阳翼间连接铰链刚度等结构参数进行动力学优化设计。经过动力学优化，有效地提高了太阳翼结构动力学特性，并改善了关键位置处动力学环境。

1 脉冲子结构与有限元子结构动力学综合方法

脉冲子结构方法的基本思路是通过子结构的脉冲响应函数与子结构所受的全部外载荷的卷积对子结构的运动进行描述，并通过界面相容条件在时域内进行子结构综合得到系统的位移响应[6]。文献[14]进一步拓展了脉冲子结构与有限元子结构的综合。

1.1 子结构的运动学描述

零初始条件下，t时刻子结构的位移可由它的脉冲响应函数与全部外载荷卷积获得

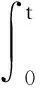
(1)

其中，上标s表示该量属于第s个脉冲子结构，u表示位移列阵，H为子结构脉冲响应函数矩阵，f为子结构受到的外力列阵，g为作用在子结构上的界面力列阵。

对于有限元子结构，它的运动方程可以表示成

f(r)(t)+g(r)(t)

(2)

其中，上标r表示该量属于第r个有限元子结构，M、C、K分别为子结构的质量、阻尼、刚度矩阵。

1.2 界面相容条件及子结构综合方程

子结构在连接界面处应满足位移协调，力平衡的界面相容条件。可将各子结构连接自由度投影到广义铰链处，通过广义铰链对各子结构进行综合[14]，如图1所示。

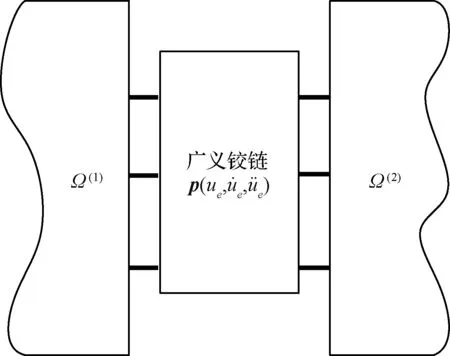
图1 子结构间的广义铰链连接Fig.1 Assembly of substructures through general joints

整个系统位移向量u由脉冲子结构位移向量与有限元子结构位移向量共同构成。对于广义铰链中的刚性连接，其界面相容条件应为连接位置处位移相等

BRu(t)=0

(3)

其中，BR为布尔矩阵，包含元素0、1、-1。

在非刚性连接位置处，将系统自由度投影到广义铰链处，广义铰链处的位移协调及力平衡方程分别为

BEu(t)=ue(t)

(4)

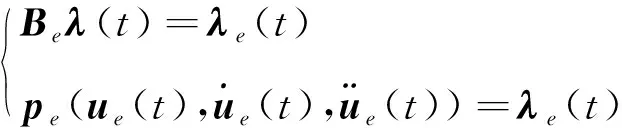
(5)

其中，BE为布尔矩阵，包含元素0、1，它将系统自由度投影到广义铰链非刚性自由度ue上；引入拉格朗日乘子λ表示作用于子结构上的界面力，通过布尔矩阵Be将其投影为非刚性连接处的作用力λe；pe为广义铰链处的运动量与作用力的关系式。

结合子结构运动学方程及界面相容条件，得到脉冲子结构与有限元广义铰链连接的综合方程

(6)

其中，布尔矩阵B将各子结构自由度投影到对应子结构连接处的自由度上，包含刚性及非刚性连接自由度。

1.3 子结构综合方程数值求解

对方程采用如下差分格式

(7)

其中，Δt为时间步长，下标n表示该量处于nΔt时刻。分离出λn得到方程(7)的递推格式

(8)

其中，

(9)

对方程(2)引入Newmark积分策略

(10)

其中，积分常数γ=0.5,β=0.25。将方程(10)代入方程(2)，可得到递推格式

(11)

其中，

(12)

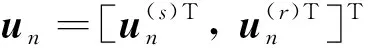
Gλn-q=0

(13)

其中，

(14)

容易看出，当pe为运动量与作用力的线性关系时，方程为线性代数方程，可直接求解；当pe为运动量与作用力的非线性关系时，可通过迭代的方法求解非线性方程，本文采用常用的Newton-Raphson方法求解。得到λn后，将其代入方程(7)、方程(11)即可得到各子结构nΔt时刻的位移。由方程(10)进一步可以获得系统nΔt时刻的速度、加速度。

2 月球探测器建模及着陆段结构动力学分析

本文研究的月球探测器由探测器中心体、着陆缓冲机构和有效载荷等部分组成[15]。根据探测器着陆动力学响应分析要求，对探测器结构进行有限元建模，如图2所示，保留探测器中心体主结构、太阳翼结构及着陆缓冲系统，其中太阳翼、缓冲腿分别通过弹性铰链、球铰与中心体连接，探测器上其他有效载荷按其安装情况以等效质量形式分布到临近承力结构上。详细有限元建模过程参见文献[16]。

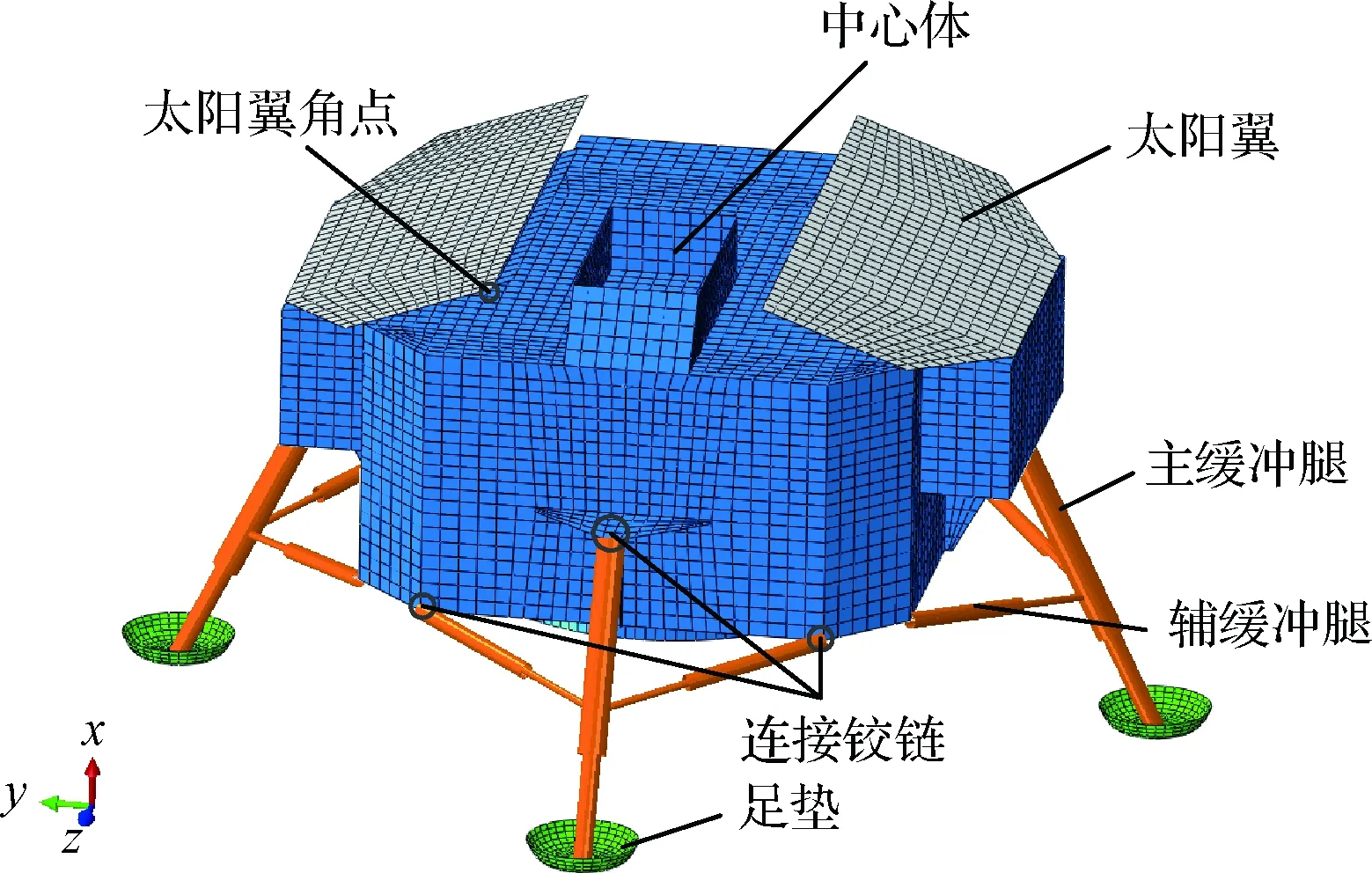
图2 月球探测器示意图Fig.2 Configuration of lunar lander

太阳翼基板是支撑太阳能电池的主承力结构，关系着探测器在月面工作的能源供应。采用四节点完全积分壳单元建立太阳翼基板复合材料有限元模型，共涉及3024个自由度，模型规模并不很大。

太阳翼根部与探测器中心体通过三个铰链连接，连接处平动自由度受到刚性约束，在转轴方向上铰链提供扭转刚度，其刚度具有一定非线性，可建立连接元表示转角与扭转力矩的三次多项式关系[17]

τ=μ1θ+μ2θ3

(15)

其中，θ为太阳翼与中心体相对转角，μ1、μ2分别为铰链线性及三次扭转刚度值。

探测器中心体以及内部的贮箱均为板壳结构，可近似作为线弹性结构建模。完整的探测器中心体有限元模型自由度众多，但涉及的连接自由度较少，着陆腿、太阳翼与中心体分别有36、24个连接自由度，可将中心体进行自由度缩聚，以提高动力学求解效率。由于中心体模态密集[14]，使用模态综合法将保留过多模态，且计算精度不能得到有效保证。因此，使用脉冲子结构方法对探测器中心体建模，共涉及60个输入自由度(所有连接自由度)、25个输出自由度(24个连接太阳翼自由度与1个中心体顶板输出自由度)。

在进行探测器中心体脉冲子结构生成时，分别在探测器中心体60个输入自由度上施加等效脉冲载荷(即初始时刻在输入自由度上直接施加载荷幅值为2/Δt的力，随后的时间步上载荷设置为零，该等效脉冲载荷称为初始载荷模型[10])，通过Newmark积分获得探测器中心体25个输出自由度上的位移响应，该系列位移响应构成了探测器中心体脉冲响应函数矩阵。

探测器着陆月面时产生的冲击载荷通过着陆缓冲系统吸收后传递到探测器主体并引起结构振动。由于两太阳翼质量不足探测器总质量的1%，其质量的改变对着陆过程中的缓冲作用力影响很小，在对探测器进行结构动力学分析时，可直接将获得的着陆缓冲力作为激励作用于缓冲腿与探测器中心体连接的36个连接自由度上。探测器在以4 m/s的初始速度竖直着陆月面(月球重力加速1.63 m/s2)时，缓冲机构对中心体的缓冲载荷，以Z+方向上主缓冲腿缓冲载荷为例，如图3所示。

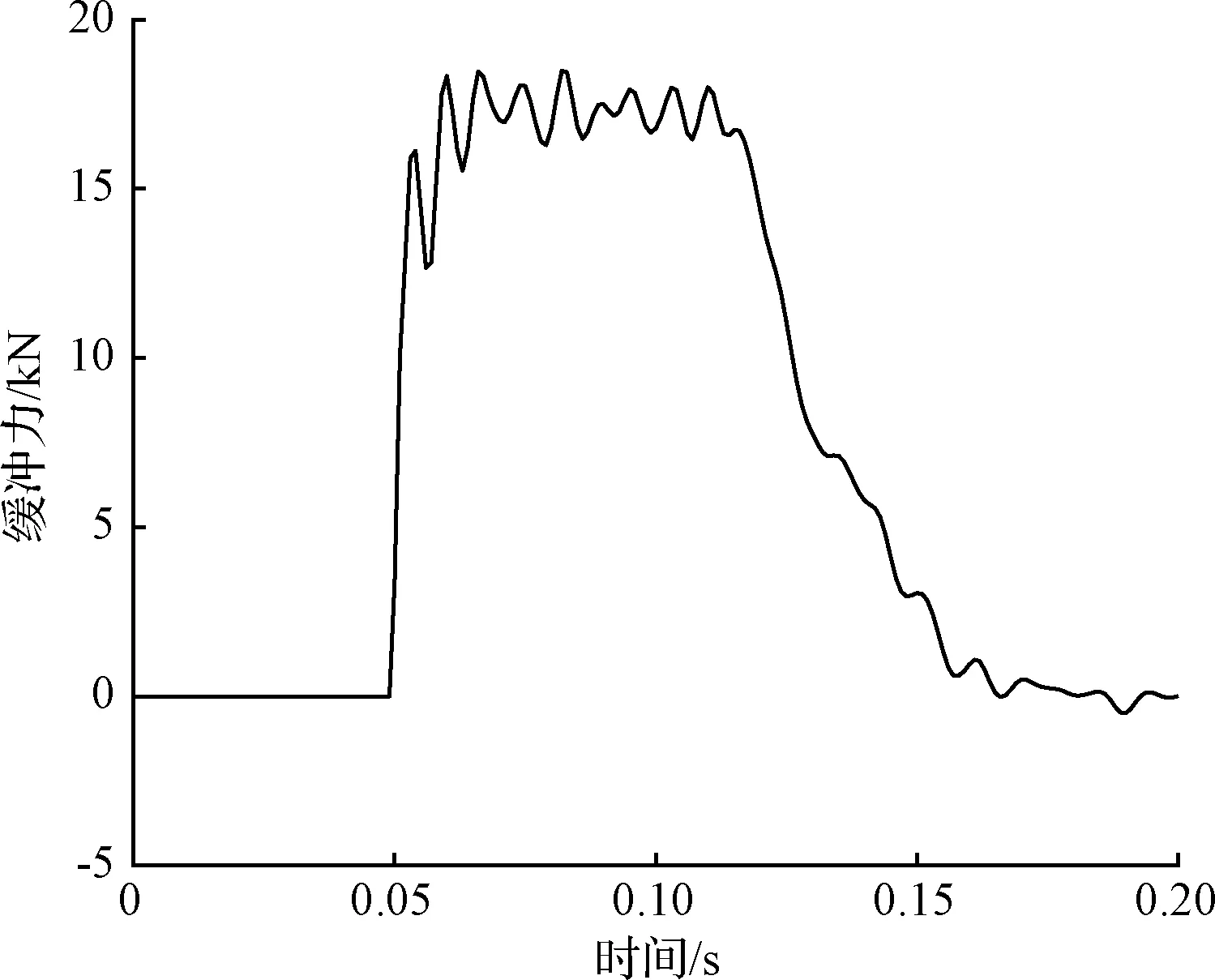
图3 着陆缓冲载荷Fig.3 Landing buffer load

通过以上分析，建立了探测器着陆段子结构动力学分析模型：探测器中心体为脉冲子结构，太阳翼为有限元子结构，子结构间为非线性的广义铰链，着陆缓冲载荷为系统激励。由于该模型在保证与有限元模型同等求解精度的前提下，极大的提高了求解效率[14]，为太阳翼结构动力学优化提供了模型基础。

3 月球探测器太阳翼结构动力学优化模型

太阳翼是月球探测器上最为关键的结构之一。在太阳翼结构设计阶段，其动力学特性越来越引起设计人员的关注。在着陆段，月球探测器太阳翼将承受较大的着陆冲击载荷，本节以第2节建立的探测器子结构动力学分析模型为基础，通过合理设计太阳翼结构参数，提高太阳翼抗着陆冲击载荷的能力。

太阳翼基本构型如图4所示。为有效降低基板质量提高基板刚度，基板采用铝蜂窝夹层板结构。基板中间层为铝蜂窝夹芯，材料参数如表1所示；夹芯两侧按照[0/90/45/-45/0/90/45/-45/]s的对称方式铺设多层碳纤维铺层，采用表2中的材料参数。

在太阳翼安装压紧点处，为保证刚、强度要求，需进行加固处理，因此，太阳翼基板采取分区域铺层的策略，在不同区域铺设不同厚度碳纤维层。基板铺层厚度、铺层方向及铺层的分布等都对太阳翼结构性能产生影响，在结构设计中应当予以考虑。

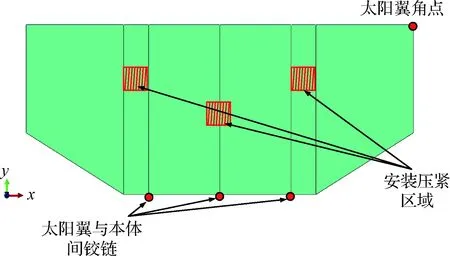
图4 太阳翼构型示意图Fig.4 Configuration of the solar wing

表1 铝蜂窝夹芯材料参数Table 1 Material property of aluminum honeycomb core

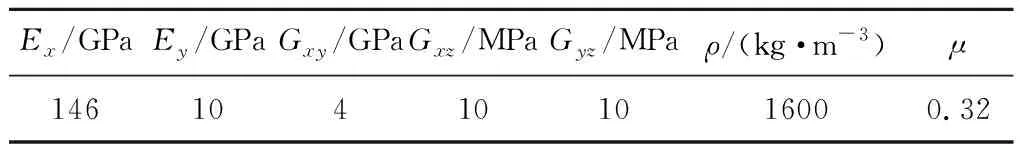
表2 碳纤维材料参数Table 2 Material property of carbon fibre

3.1 优化目标选取

本次太阳翼结构动力学优化旨在提高太阳翼抗着陆冲击载荷的能力，使得太阳翼基板安装压紧区域冲击力学环境最小，保证太阳翼结构及有效载荷在动态冲击过程中结构性能完好。在探测器着陆冲击力学环境分析中，通常使用加速度冲击响应谱(Shock Response Spectrum，SRS)对探测器部组件处的冲击力学环境进行量化[2,18]。因此对安装压紧区域内特征点的加速度冲击响应谱进行包络，使用该包络谱描述安装压紧区域着陆冲击力学环境。

综合以上分析，太阳翼结构动力学优化目标选取为：

minAf

(16)

其中，Af为安装压紧区域特征点加速度冲击响应包络谱峰值。

3.2 约束条件选取

在对太阳翼结构动力学优化时，主要对包括太阳翼的质量特性、动响应及结构固有频率有如下要求：

1)质量特性要求：考虑到运载火箭运载能力，探测器总质量应尽可能轻，太阳翼结构总质量Ms应当控制在分配的质量指标之内；

2)动响应要求：探测器着陆过程中，在冲击作用下太阳翼会有一定幅度振动，为保证太阳翼与探测器本体不发生物理干涉，太阳翼角点处相对位移d应在可控范围之内；

3)固有频率要求：在太阳翼展开过程中，为保证太阳翼与驱动机构的动力学特性更加匹配，不发生严重的耦合，太阳翼一阶绕铰链转动基频Hf应大于驱动频率。

3.3 太阳翼结构动力学优化设计变量分析

太阳翼是探测器的主要供能装置，基板上布有太阳能电池片，其形状和总面积与所需太阳能电池片的面积和布局相适应[19]，所以在结构动力学优化设计中不涉及其几何外形参数。太阳翼基板采用分区域铺层结构设计，其中碳纤维铺层厚度对太阳翼结构刚度、强度影响显著，在已满足静强度基础上(单层碳纤维铺层厚度下限满足静强度要求)，对太阳翼局部单层碳纤维铺层厚度(h1,h2)进行优化设计；太阳翼整体刚度同时受到太阳翼与本体间连接铰链扭转刚度的影响，由于探测器着陆过程中太阳翼相对转动较小，三次扭转刚度对动响应影响较小(此处取值设为6000 N/rad3)，因此仅对一次扭转刚度(μ1)进行优化。综合以上，设计变量及设计空间如表3所示：

表3 太阳翼结构动力学优化设计变量Table 3 Dynamic optimum design variables of solar wings

3.4 探测器太阳翼结构动力学优化数学模型

通过以上对优化三要素：优化目标、约束条件、设计变量的分析，太阳翼结构动力学优化问题可描述为标准优化数学模型：

其中Ms_max=5.5 kg,d_max=40 mm,Hf_min=16 Hz。

4 探测器太阳翼结构动力学优化分析

探测器太阳翼结构动力学优化流程总结如下。首先确定优化初始条件，包括设计变量、目标函数、约束条件和设计空间等；接着，建立高效求解的动力学响应预测模型：由于探测器本体自由度众多、涉及较多内部连接且在太阳翼动力学优化设计时保持结构不变，因此将探测器本体凝聚成脉冲子结构，太阳翼采用有限元建模，探测器本体与太阳翼通过广义铰链连接，通过脉冲子结构方法对动力学响应进行预测；然后，选取合适优化算法调用动力学响应预测模型进行优化求解。

在本优化算例中涉及3个连续设计变量、3个非线性约束及1个目标函数，其中目标函数加速度冲击响应包络谱峰值由于经过统计包络运算不是设计变量的连续函数，因此本节可选用遗传算法(GA)对该问题进行寻优，遗传算法能够处理此类不连续、非线性问题且具有较好的全局寻优能力；同时，采用罚函数法对约束进行处理，将该约束优化问题转换成等价的无约束优化问题。具体优化流程如图5所示。

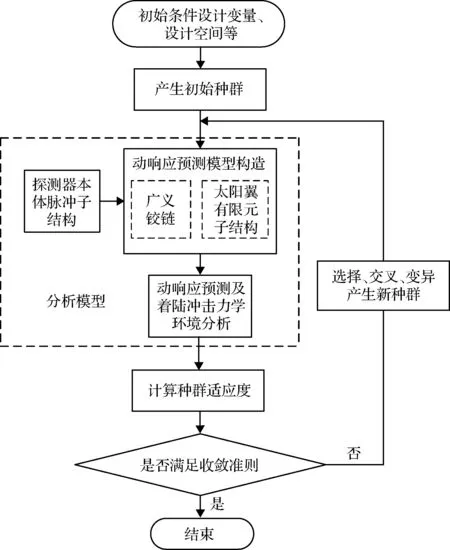
图5 探测器太阳翼结构动力学优化流程Fig.5 Optimization process of the dynamic optimum design of solar wings

采用遗传算法对该问题进行寻优：种群设置为30，代数为50代。种群适应度随种群代数的变化曲线如图6所示，可以看出，种群代数到达40代后，结果基本收敛。

图6 种群适应度收敛曲线Fig.6 Iterative convergence curve of fitness value

经过优化求解，得到优化后的设计变量，如表4所示。

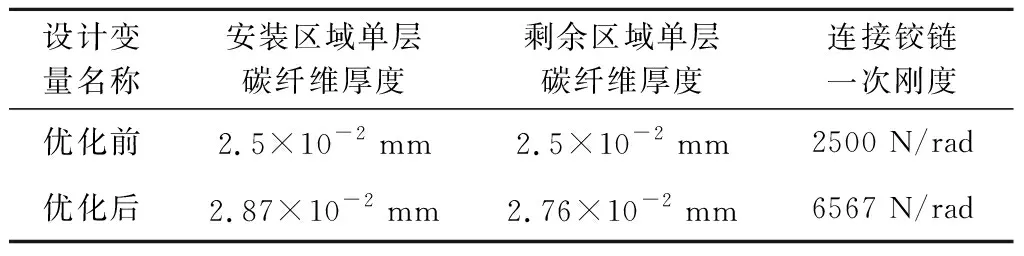
表4 优化前后设计变量取值Table 4 The design variables before and after the optimization

优化后太阳翼动力学特性各指标均有所提高，太阳翼绕铰链转动基频及太阳翼角点相对最大位移均满足约束要求，总质量在满足约束要求前提下略有增加，太阳翼安装压紧区域冲击响应包络谱峰值由降低了约1 km/s2，着陆冲击力学环境得到有效改善，具体如表5所示。

表5 优化前后结构动力学特性对比Table 5 The structural dynamic performance before and after the optimization

整个寻优过程共调用模型1530次，单次模型分析耗时约90 s。若动力学分析模型采用原有限元模型，仅单次动力学响应预测将耗时约1400 s，这将使得整个优化过程极其耗时、不可接受。

5 结 论

本文通过引入脉冲子结构方法，建立了探测器着陆段结构动力学子结构分析模型，并基于此快速分析模型对探测器太阳翼结构进行动力学优化。首先分析选取了探测器太阳翼结构动力学优化三要素，将太阳翼绕铰链转动基频、太阳翼角点最大相对位移、太阳翼总质量作为约束，建立了以太阳翼安装压紧区域冲击响应包络谱峰值为目标函数的优化数学模型；接着提出了探测器太阳翼结构动力学优化流程，将脉冲子结构方法引入优化过程，在保证与有限元模型同等求解精度前提下，使得单次动力学分析效率提高15倍以上，显著缩减了结构动响应计算耗时；最后完成优化分析，得到合理的结构设计参数，太阳翼动力学特性各指标均有所提高，太阳翼安装压紧区域着陆冲击力学环境得到有效改善。结果表明，脉冲子结构方法可以有效应用到结构动力学特性优化分析中，提高结构设计优化效率，所得优化结果对实际结构设计具有一定指导意义。