一般三棱镜偏向角与入射角的关系

王梦影,顾菊观,徐海斌,曹炳松,俞轶帆

(湖州师范学院 理学院,浙江 湖州 313000)

0 引 言

在《光学》[1]和《光学实验》教材[2]中,对三棱镜的讨论都是针对等边三棱镜及其在空气中偏向角、最小偏向角与入射角的关系.在实验和教学过程中,教师和学生很难从理论上解释偏向角与入射角的关系曲线,也很难从光线传播轨迹上进行分析.文献[3]研究了空气中等边三棱镜入射角、棱镜顶角、折射率的变化对偏向角的影响.文献[4]讨论了空气中等边三棱镜偏向角与入射角、棱镜折射率的关系,以及最小偏向角与顶角、折射率的关系.文献[5]探讨了空气中等边三棱镜偏向角与入射角的关系,并得到其最小入射角.文献[6]研究了空气中等边三棱镜偏向角与入射角的关系,以及最小入射角与棱镜顶角、折射率的关系.文献[7]讨论了空气中等边三棱镜偏向角与入射角的关系,得到测量偏向角需要考虑棱镜顶角、折射率、入射角和入射点等因素.文献[8]通过推导得到了一般三棱镜的最小入射角、最大顶角和折射率要求.文献[9]讨论了影响棱镜顶角和最小偏向角测量的因素.文献[10]和[11]分析讨论了空气中三棱镜折射率、入射角的测量方法,以及测量中的入射点问题.以上教材和文献都没有对曲线的各部分进行理论分析和光路模拟分析,也没有对一般三棱镜的具体情况进行分析讨论.本文应用几何光学原理,得到在顶角、两侧折射率和自身折射率不同的情况下,一般三棱镜偏向角和最小偏向角的理论公式,并运用Matlab研究偏向角与入射角的关系曲线,以及运用TracePro模拟光线传播分析讨论关系曲线和光线轨迹,观察入射角、顶角和折射率变化对出射光线出射的影响.

1 理论分析

1.1 偏向角与入射角、出射角、顶角的关系

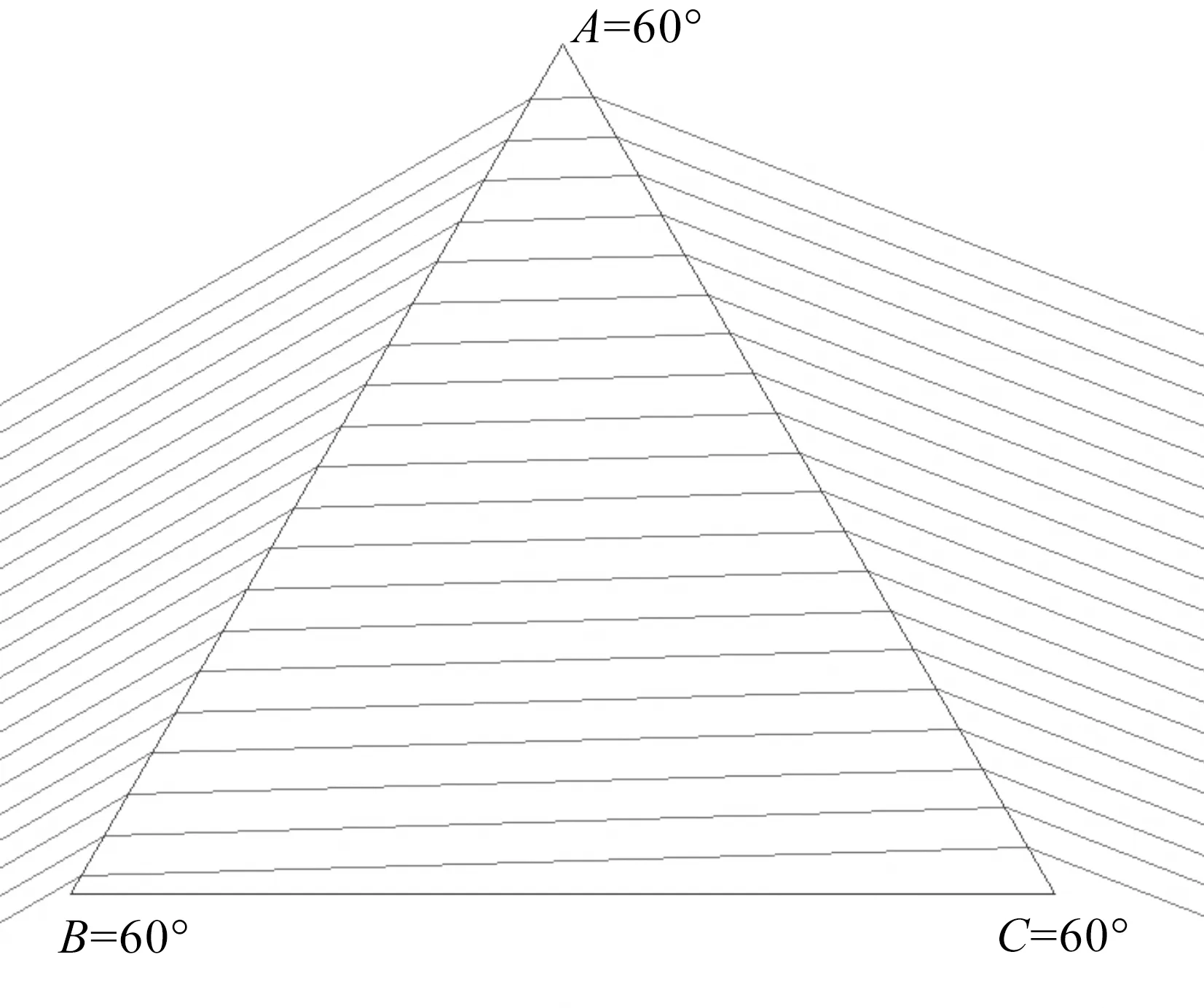
一般三棱镜的光路示意图见图1.A、B、C为三棱镜的三个角,A为顶角,B、C为底角.i1为AB面的入射角,r1为AB面入射角i1对应的折射角,O点为AB面的入射点.r2为AC面的入射角,i2为AC面入射角r2对应的出射角,E点为AC面上的入射点.θ为出射光线与入射光线的夹角,即偏向角.α为AB面法线与AC面法线的夹角,两法线交点为F点.n2为三棱镜的折射率,n1、n3分别为棱镜两侧的折射率.

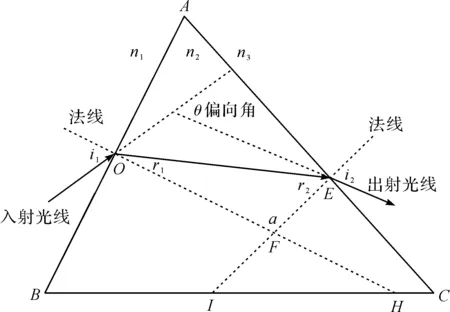
图1 一般三棱镜的光路示意图

由图1和几何关系得:

r1+r2=A.

(1)

偏向角θ为AB面的入射光线经AB面折射和AC面折射对应的出射光线,以锐角逆时针转至入射光线延长线所对应的夹角,且为正值[1-11].偏向角θ与入射角、出射角、顶角的关系为:

θ=(i1-r1)+(i2-r2)=i1+i2-(r1+r2)=i1+i2-A.

(2)

由此可得,偏向角θ与B、C角没有关系,而与入射角、出射角和顶角有关.该结果与空气中等边三棱镜的研究结果[1,3,5-7]一致.

1.2 偏向角与入射角、顶角的关系

由式(1)、式(2)和折射定律式(3):

(3)

化简得:

(4)

将式(4)代入式(2),得偏向角与入射角、顶角的关系:

(5)

式(5)表明了一般三棱镜的偏向角θ与入射角i1、顶角A,以及折射率n1、n2、n3的关系,说明偏向角θ与折射率n1、n2、n3是有关系的,测量偏向角时需要选择合适的入射角、顶角和折射率.

1.3 最小入射角与最大顶角的关系

文献[8]通过讨论得到了最小入射角i1min、最大顶角Amax和折射率要求,即:

ICP-OES法同时测定煅炉甘石中氧化锌及13种金属元素杂质的含量 ……………………………………… 谢 凯等（16）：2179

(6)

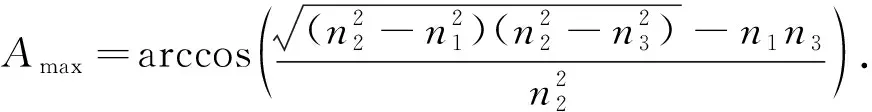
(7)

折射率要求:

n1n3.

(8)

式(6)指在给定折射率和棱镜顶角时,当AC面产生全反射时AB面对应的最小入射角i1min,即若要在AC面观察到折射光线(出射光线),则对应AB面的入射角应大于最小入射角i1min.式(7)指在给定折射率时,若要在AC面观察到折射光线(出射光线),则对应的棱镜顶角必须小于最大棱镜顶角Amax.式(8)指在AC面观察到折射光线(出射光线)且偏向角为锐角正值的情况下,对应的折射率关系为棱镜的折射率必须大于两侧的折射率.

1.4 最小偏向角与入射角的关系

对式(2)两端的i1进行求导,得:

(9)

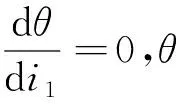
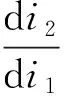
(10)

对式(1)求微分,得:

dr1+dr2=0.

(11)

对式(3)求微分并化简,将式(10)和式(11)代入式(3),得:

(12)

将式(12)平方后,得:

(13)

(14)

将式(3)平方后,代入式(14)化简,得:

(15)

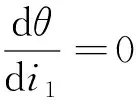
当n1=n3=1时,式(14)可化简为sini1=sini2,则i1=i2,与空气中等边三棱镜最小偏向角的条件[1-2,6-7,10-11]相同.

由式(15)可得:

(16)

将式(16)代入式(2),得到最小偏向角:

(17)

式(17)中的θmin是满足一定入射角[式(16)出射角对应的入射角]时对应的最小偏向角.式(17)说明最小偏向角θmin与三棱镜的底角B、C无关,而与入射角i1、顶角A,以及棱镜的折射率n2、两侧的折射率n1、n3有关.

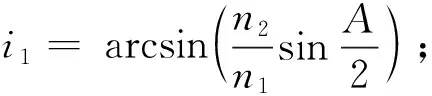
2 偏向角与入射角的关系曲线和模拟光路

当给定棱镜折射率、两侧折射率和棱镜顶角时,偏向角θ与入射角i1的关系由式(5)确定.但要考虑对应的最小入射角i1min和棱镜最大顶角Amax[4-8],才能直观正确地得到关系曲线,才能在AC面观察到出射光线.由式(6)可得到给定棱镜的最小入射角i1min,由式(7)可得到给定棱镜的最大顶角Amax.

2.1 n1=1,n2=1.647 5,n3=1,A=60°,Amax=74.743 0°

图2中偏向角与入射角的关系曲线与文献[3-6]中的关系曲线相似,其中直线部分对应的是AC面发生全反射的情况.图3、图4中的D点是指棱镜内的折射光线(粗的黑线)刚好入射到棱镜的C点所对应的入射点.D点和BD区间内的入射光线经BC面反射,再经AC面折射,在AC面观察到出射光线,此时偏向角不是文献[1-5,7-8,11]及本文所定义的偏向角;D点和BD之间的区域大小与入射角、折射率、顶角有关,关于D点位置和BD之间区域大小的研究将另文探讨.这就要求在实验和教学过程中,要注意入射角i1应大于最小的入射角i1min,且入射点在AD之内(图4、图5)时,才能在AC面能观察到出射光线,且偏向角θ为文献[1-5,7-8,11]和本文所定义的偏向角θ.由图2可知,当入射角i1大于最小入射角i1min时,偏向角θ随入射角i1的增大而非线性地减少;当入射角i1满足式(15)的条件时,偏向角θ达到最小值θmin;当入射角i1继续增大时,偏向角θ也随之非线性地增大.

注:空气中的等边三棱镜,A=60°,n2=1.647 5.图2 偏向角θ与入射角i1的关系曲线

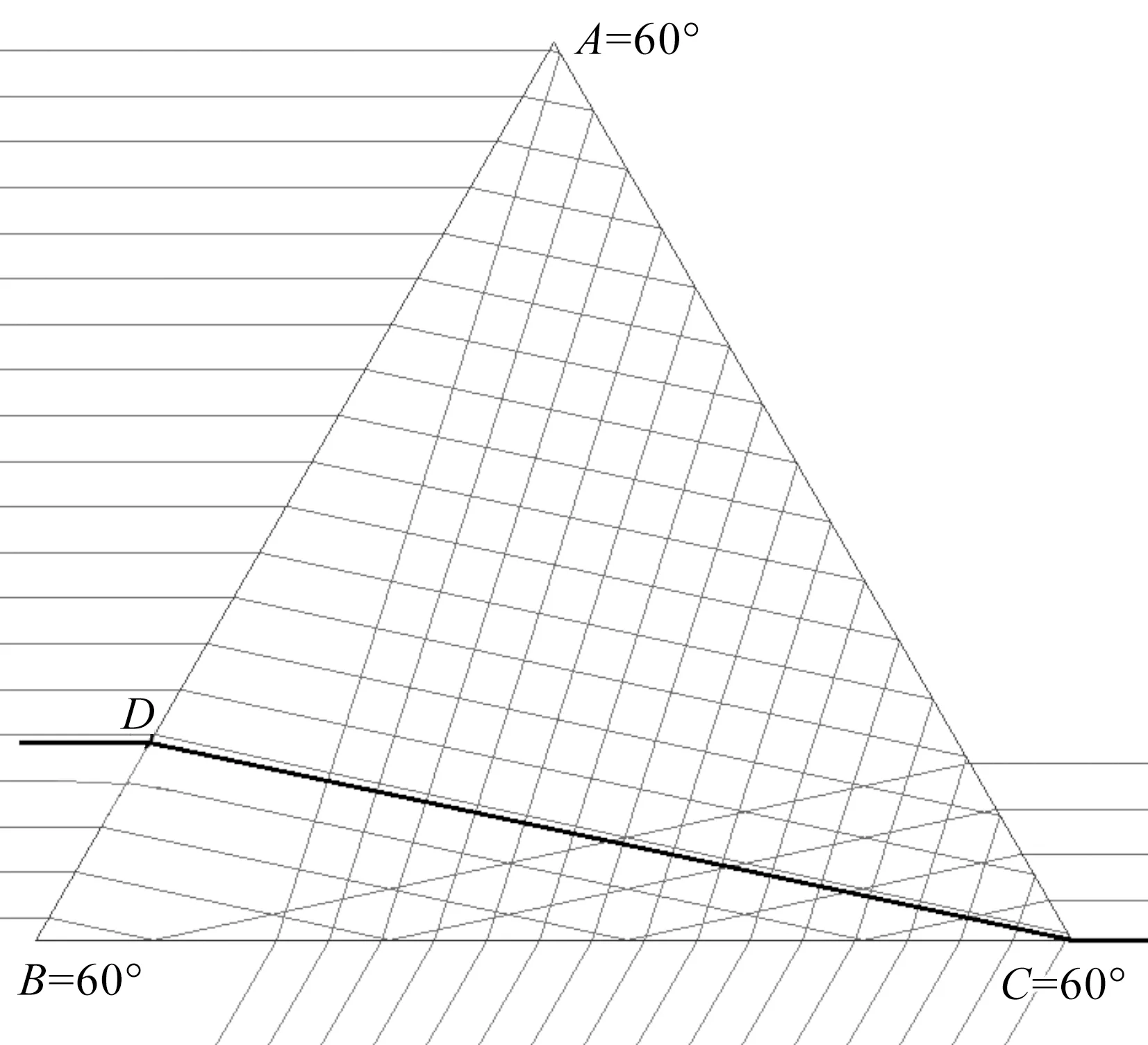
注:在空气中,入射角i1=30°.图3 等边三棱镜的光路轨迹示意图

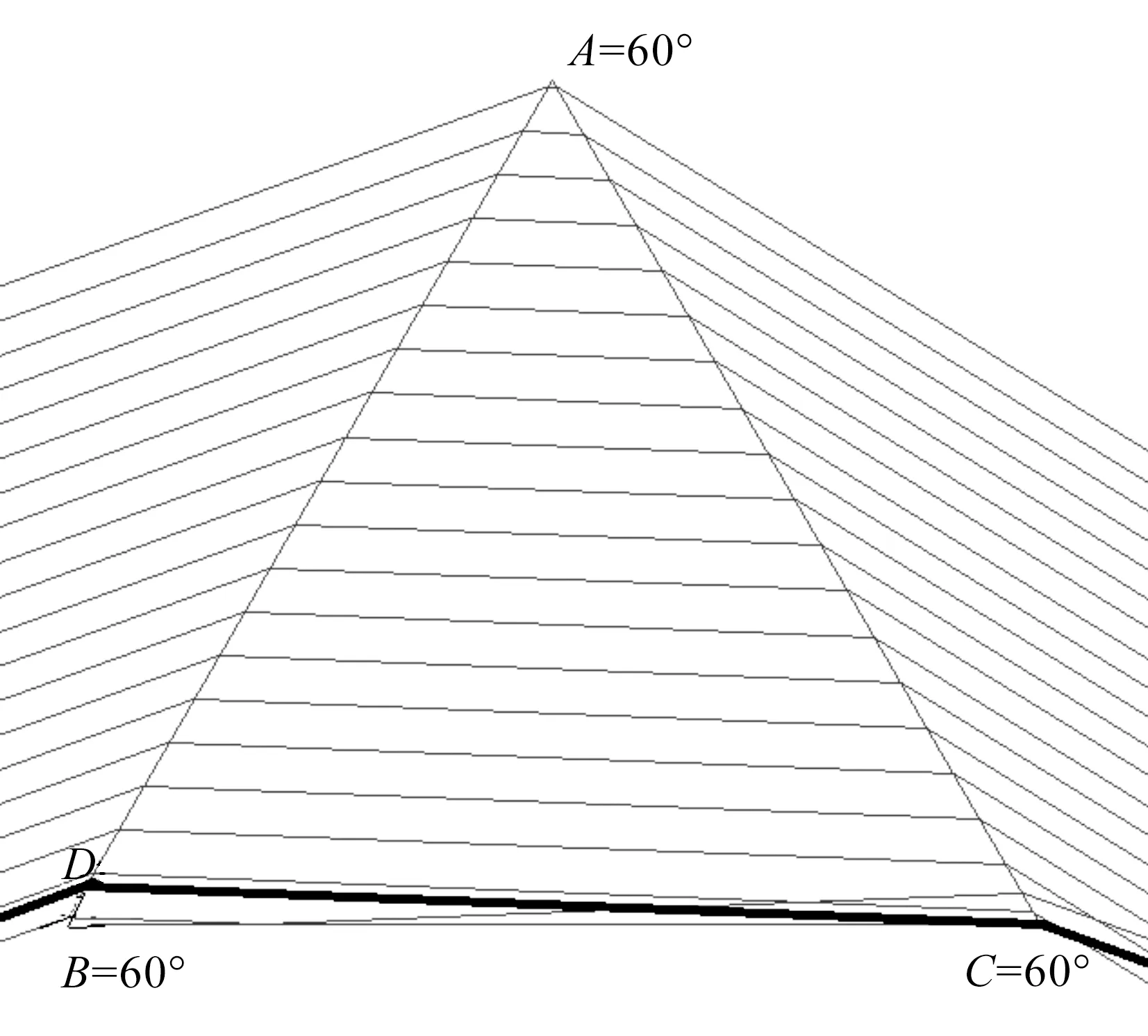
注:在空气中,入射角i1=50°.图4 等边三棱镜的光路轨迹示意图

注:在空气中,入射角i1=60°.图5 三棱镜的光路轨迹示意图

图2中的直线部分因在AC面发生全反射,故出射光线从BC面出射(图6).对应的偏向角θ是虚数,取实部为:

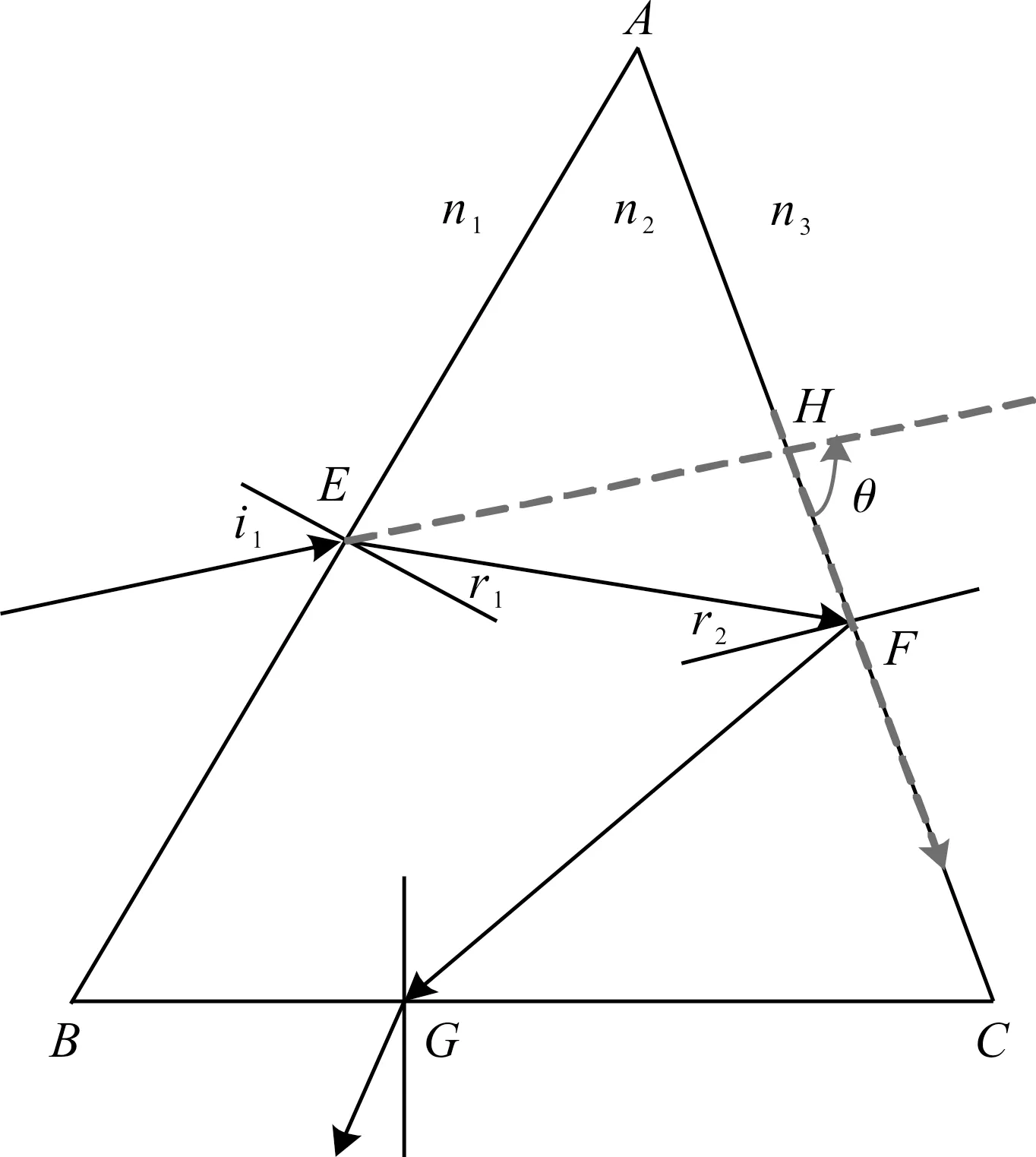
图6 全反射对应的偏向角光路示意图

(18)

实际上,此时的偏向角θ对应图6中的FH线与入射光线EH线的夹角.由图6可得:

(19)

式(18)的Matlab计算结果与式(19)一致.由式(19)可知,对给定的棱镜顶角A,此时的偏向角θ与入射角i1有关,且为线性关系,并对应于图2的直线部分.式(19)的理论分析与关系曲线相符.以下的偏向角θ与入射角i1的关系曲线(图6中的直线部分)分析都与此相同.

2.2 n1=1,n2=1.647 5,n3=1,A=74°,Amax=74.743 0°

图7为当棱镜顶角接近顶角最大值Amax时,偏向角θ与入射角i1的关系曲线.由图7可知,只要棱镜不大于最大顶角Amax,就一定会存在偏向角θ随入射角i1由大逐渐减小至最小,再逐渐增大的变化过程,同时存在最小入射角i1min和最小偏向角θmin.

注:空气中的一般三棱镜,A=74°,n2=1.647 5.图7 偏向角θ与入射角i1的关系曲线

2.3 n1=1,n2=1.647 5,n3=1,A=3°,Amax=74.743 0°

图8为当棱镜顶角很小、入射角很小(i1<5°)时,偏向角θ与入射角i1的关系曲线.由图8可知,当入射角i1较小时,偏向角基本不变.由θ=(n2-1)A=(1.647 5-1)×3=1.942 5°,θmin=1.943 5°可得,偏向角θ和最小偏向角θmin基本相等,这与理论分析和文献[2,6]一致.同时,当棱镜顶角很小时,不存在全反射情况,偏向角θ与入射角i1的关系曲线没有出现直线部分.

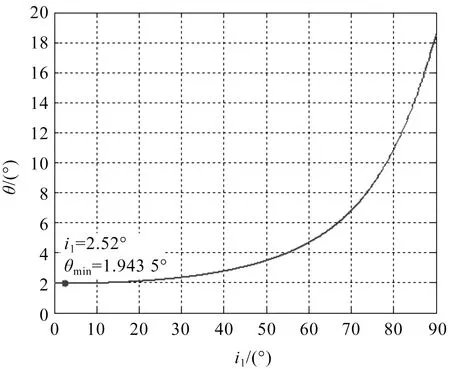
注:空气中的一般三棱镜,A=3°,n2=1.647 5.图8 偏向角θ与入射角i1的关系曲线

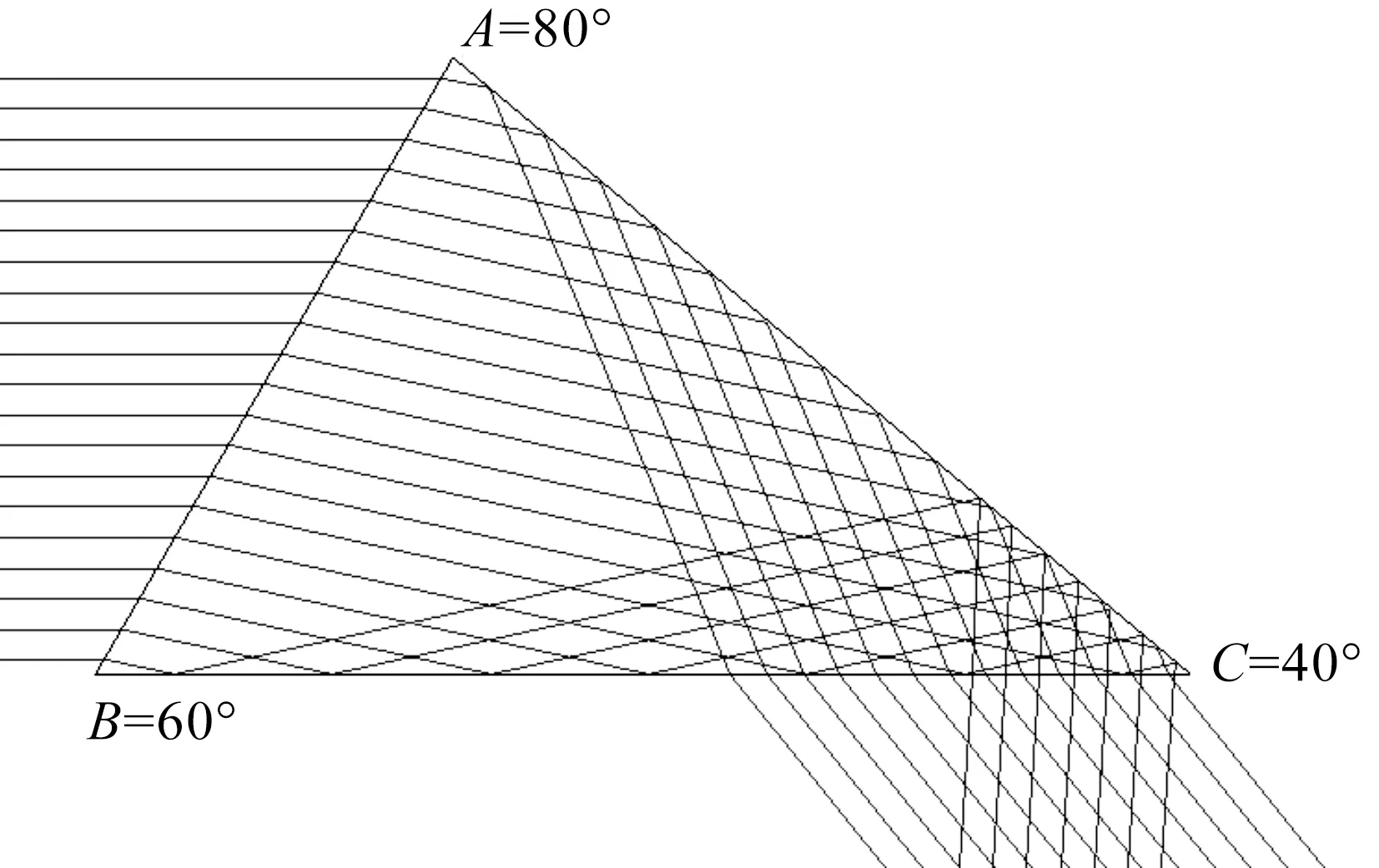
2.4 n1=1,n2=1.647 5,n3=1,A=80°,Amax=74.743 0°

图9为当棱镜顶角A大于棱镜最大顶角Amax=74.743 0°时,偏向角θ与入射角i1的线性关系曲线,其满足式(19).图10和图11说明,棱镜顶角A不能大于折射率给定情况下的棱镜最大顶角Amax,否则无论入射角θ为多大,出射光线都不能从AC面出射,对应偏向角θ也不是文献[1-5,7-8,11]定义的偏向角θ.

注:空气中的一般三棱镜,A=80°,n2=1.647 5.图9 偏向角θ与入射角i1的关系曲线

注:在空气中,入射角i1=30°.图10 三棱镜的光路轨迹示意图

注:在空气中,入射角i1=70°.图11 三棱镜的光路轨迹示意图

2.5 n1=1.333 0,n2=1.647 5,n3=1,Amax=91.380 0°

图12和图13为当棱镜两侧折射率不同时,对应棱镜顶角A为60°和91°时,偏向角θ与入射角i1的关系曲线.该关系曲线与图2相似,也存在最小入射角i1min和最小偏向角θmin.当棱镜顶角大于Amax=91.380 0°时,同样不存在文献[1-5,7-8,11]定义的偏向角θ.

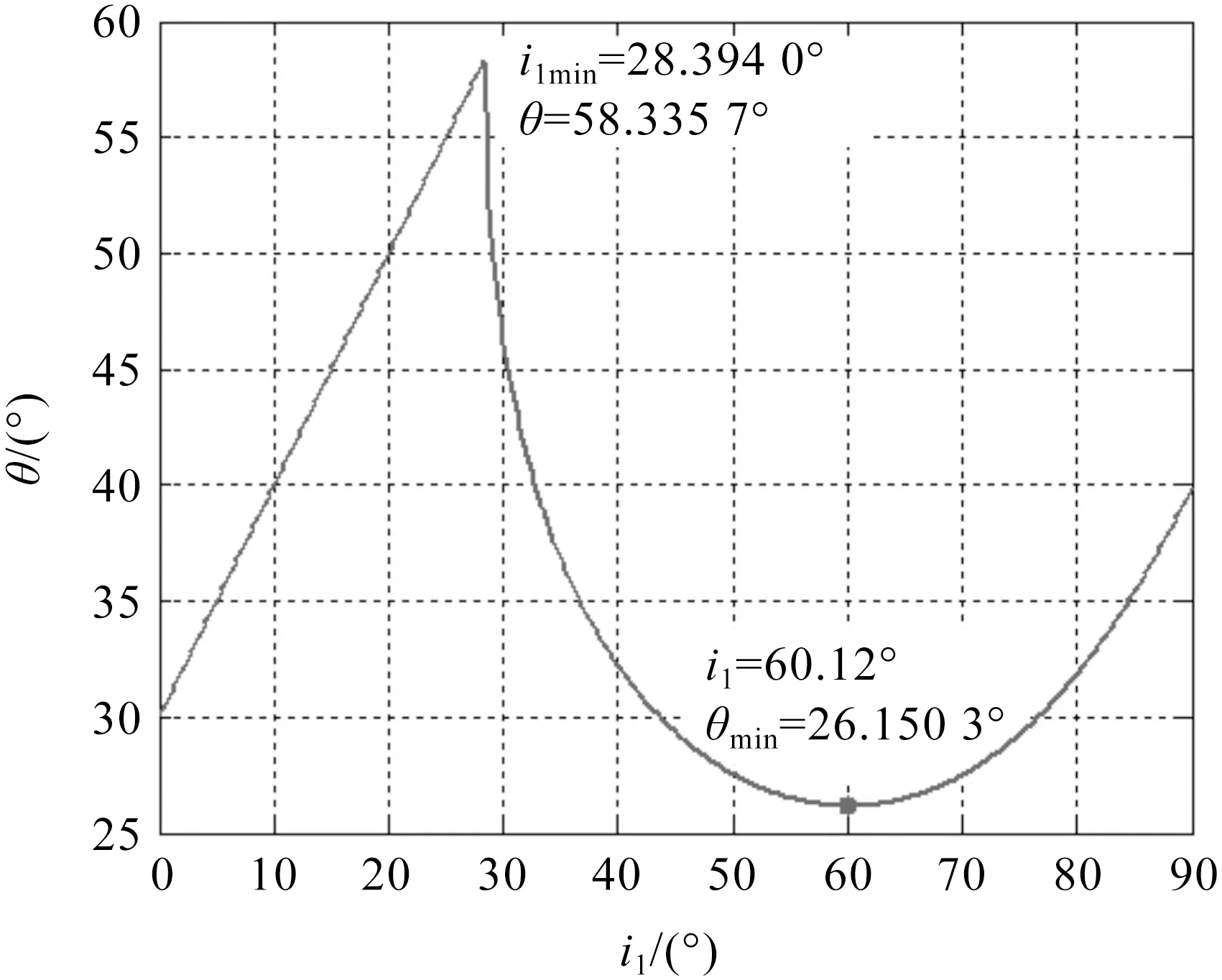
注:左侧在水中,A=60°,n2=1.647 5.图12 偏向角θ与入射角i1的关系曲线

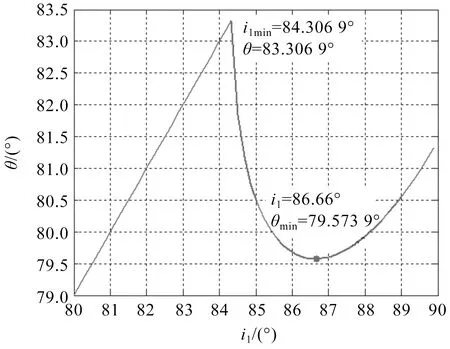
注:左侧在水中,A=91°,n2=1.647 5.图13 偏向角θ与入射角i1的关系曲线

当棱镜顶角A=91°时,由图13可知,入射角i1应大于84.306 9°,这样才能从AC面观察到出射光线,否则不能从AC面观察到出射光线.

图14对应的是入射角i1=82°,从模拟光路看出光不能从AC面出射;图15对应的是入射角i1=85°,从模拟光路看出光能从AC面出射.这与理论分析和Matlab曲线、TracePro模拟光路分析一致.

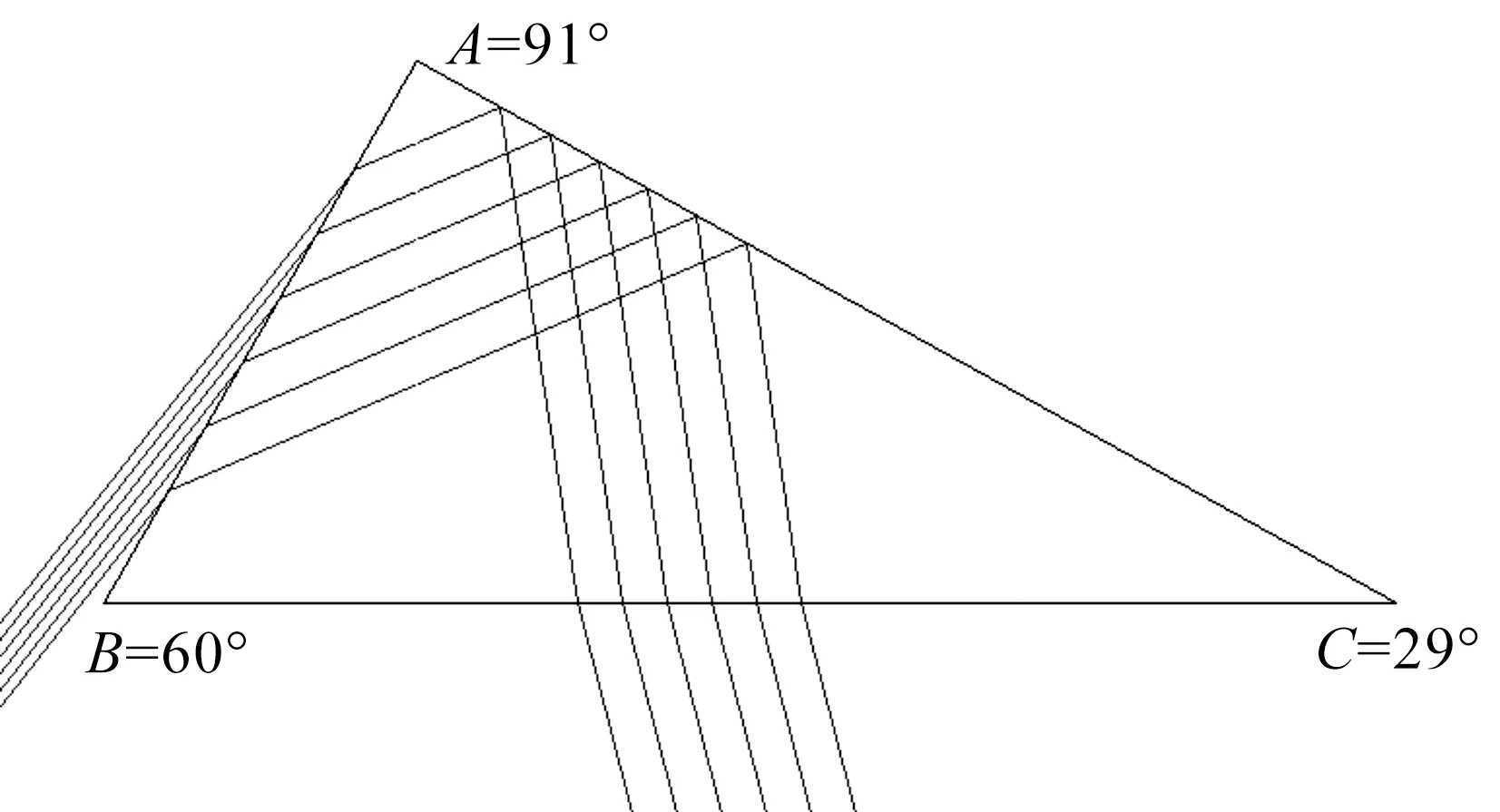
注:左侧在水中,入射角i1=82°.图14 三棱镜的光路轨迹示意图

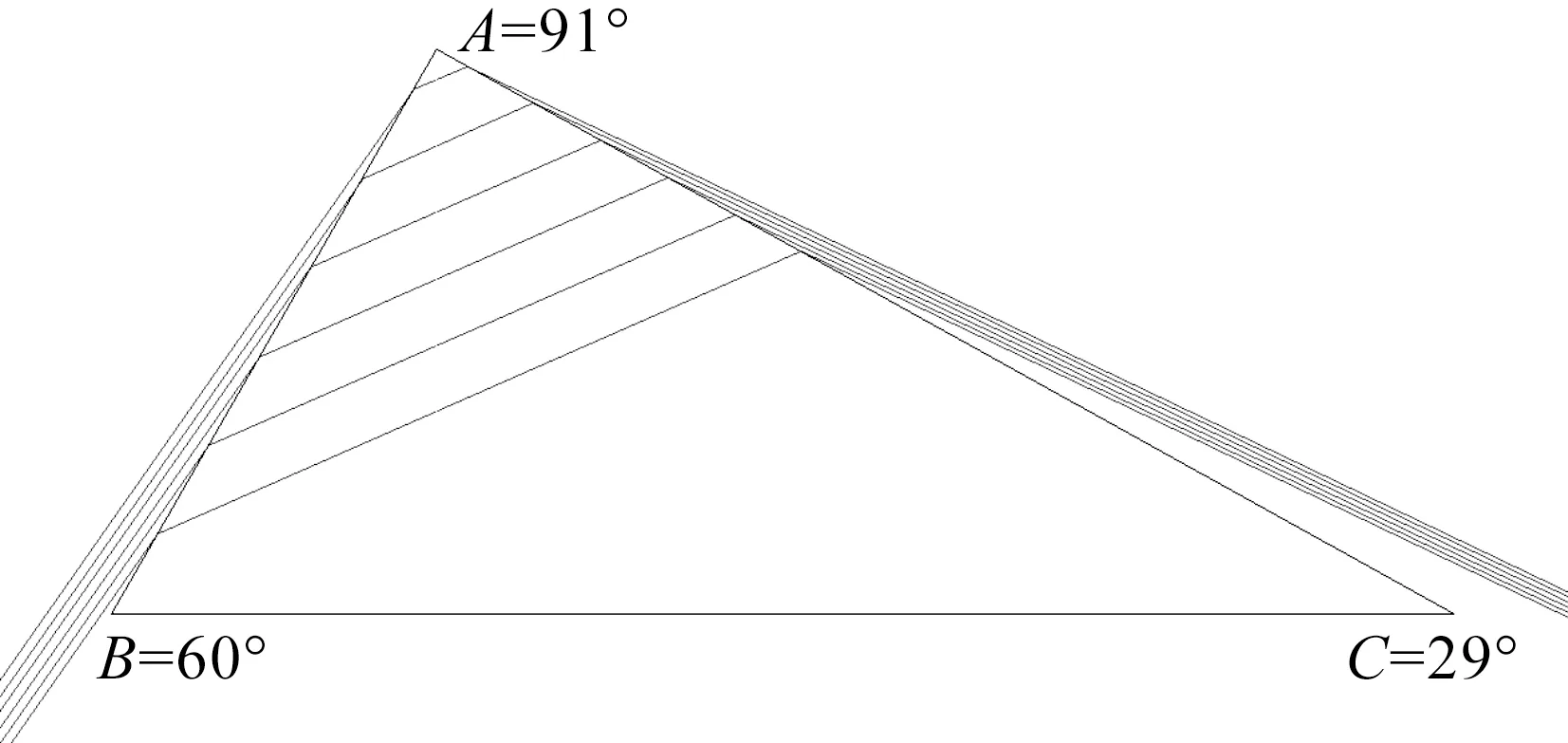
注:左侧在水中,入射角i1=85°.图15 三棱镜的光路轨迹示意图

3 结 论

本研究表明,对给定的棱镜顶角、棱镜折射率,在满足一定条件下,一般三棱镜的偏向角与入射角的关系曲线和空气中的关系曲线相似.通过模拟光路可直观地观察到光线的传播轨迹,且很容易判断和理解光是否直接从AC面折射出射,或经过其他方式从AC面出射,或从BC面出射的情况.理论分析、Matlab关系曲线和TracePro模拟光路分析表明,当入射角小于一定角度时,从AC面观察不到出射光线,对应的偏向角不是文献[1-5,7-8,11]定义的偏向角;最小入射角随顶角和折射率的改变而改变.本文理论和模拟分析了关系曲线直线部分的原因,得到入射点D也会影响出射光线.曲线和理论分析表明,最小偏向角随顶角和折射率的改变而改变,且当顶角小于5°时,其偏向角在入射角较小时基本不变.该研究结果对实验、教学及研究过程中如何选择棱镜顶角、棱镜两侧折射率及AB面上的入射角具有很好的参考价值和指导作用.