末端能量管理段迭代校正轨道算法研究

张恒浩

(1.中国运载火箭技术研究院研究发展中心,北京 100076)

0 引 言

航天器从进入大气层到返回着陆地点分为再入段、末端能量管理段和自动着陆段三部分[1]。其中末端能量管理段(Terminal Area Energy Management，简写为TAEM)位于再入段和自动着陆段之间，其任务是将大气层再入段结束时处于相对随机状态下的航天器引导到自动着陆段的接口处，并要求满足航天器在自动着陆段接口处时自身的位置、高度、速度、航向等状态约束条件[2-5,7]。航天器在末端能量管理段飞行时没有发动机提供动力，需要靠地球重力和空气动力进行能量管理控制。工程上传统的航天器TAEM轨道计算是通过将飞行器与航向校准柱(Heading Alignment Cylinder，简写为HAC)相切[6]，然后根据航天器自身能量条件提前设计航天器绕HAC轨迹并校准航向，使航天器在结束TAEM飞行时航向能够对准着陆场跑道中心线，进入自动着陆段[8-11]。

现阶段针对TAEM段轨道设计技术主要是将再入段的技术直接移植到TAEM段中，通过事先离线计算好的飞行轨道对航天器进行制导控制，并要求航天器不能在位置和航迹倾角上有较大的摄动变化[9]。单独针对TAEM段轨道计算的研究较少。近年来，国内外对TAEM段的研究主要集中在在线轨迹生成技术上[12-13]。美国NASA的高级工程师Hull等人在2015年提出模糊逻辑控制航天器进行TAEM段轨道生成设计思路。2016年另一位高级工程师Batron改进“核心提取协议”轨迹生成法并进行了仿真试验。但是上述研究方法对TAEM段轨道起始点的初始状态约束较为严格[14-17]。当航天器在起始点的位置和航迹倾角存在大范围摄动时，TAEM段在线轨迹生成技术无法进行有效的鲁棒性控制，经常会导致计算结果失控[18]。

针对这一问题，提出一种基于迭代校正的TAEM段轨道算法，首先设计制导算法，通过跟踪轨迹地面投影实现侧向制导；根据TAEM段的起始点与终点的高度与速度约束生成参考动压-高度剖面，并跟踪此剖面实现纵向制导。然后采用迭代校正计算快速确定航向校准柱的位置与最终半径调整参数，保证航天器在末端的所有状态满足自动着陆段接口的边界约束。仿真结果表明，该算法可以根据航天器的初始状态，自动选择进场策略，并调整航向校准柱的位置和最终半径，生成可行的飞行轨道。

1 运动模型设计

再入段结束后进入TAEM飞行阶段，TAEM段的轨道从气动加热并已经到达较低水平时开始，一直到航天器离开HAC，调整到水平飞行状态并对准跑道中心线为止[19]。航天器在TAEM阶段应快速高效地将位置误差与航向角度误差消除掉，并引导自身顺利进入自动着陆段[20]。

根据TAEM阶段的要求，对航天器的飞行做如下定义[17]：

1) 将地球视为惯性系统，忽略地球自转和公转，即视地球为静止；

2) 忽略地球曲面影响。

定义地面坐标系o1-xgygzg如下所示[21]：

地面坐标系的原点o1位于跑道的起点处；o1xg轴沿着跑道中心线的方向为正；o1yg轴位于跑道平面内，与o1xg轴垂直，指向右方为正；o1zg轴在跑道地面以下，与o1xg轴和o1yg轴形成右手定则。

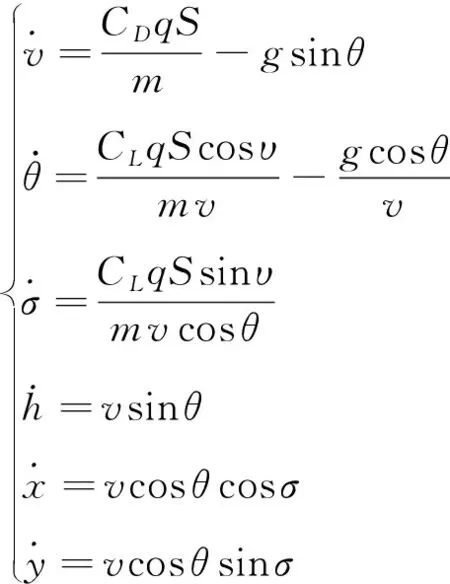
(1)

在地面坐标系中，设航天器的三自由度运动方程如方程组(1)所示[22]。

方程组(1)中，x,y分别表示航天器在地面坐标系中的位置，h表示相对跑道平面的高度，θ表示航迹倾角，σ表示航迹偏角，α表示攻角，β为侧滑角，υ表示倾侧角，m表示航天器质量，S表示航天器特征面积，CL表示升力系数，CD表示阻力系数。

(2)

升力系数和阻力系数的计算公式如式(2)所示。式(2)中，M表示马赫数[23]。

2 算法设计

航天器在TAEM阶段的轨道算法需要根据航天器的初始状态，选择直接进场方式或者间接进场方式，并快速生成可行的参考轨迹[24]。算法通过跟踪轨迹地面投影实现侧向制导；根据末端能量管理段的起始点与终点的高度与速度约束生成参考动压-高度剖面，并跟踪此剖面实现纵向制导；调整HAC的圆心位置与最终半径来调整整个TEAM阶段的航程，使其在到达TAEM阶段终点时满足自动着陆段处的状态约束，达到返航能量管理的要求[25-27]。

2.1 制导设计

制导设计分侧向制导和纵向制导两部分。

2.1.1侧向制导

侧向制导设计包括捕获段、航向校准段和进场前飞行段三段设计。捕获段飞行是控制航天器向HAC表面飞行，以便飞行轨道和HAC的表面某点相切。航向校准段的目的是使航天器沿着HAC表面飞行，同时通过动压和速度制动的变化控制其能量。进场前飞行段负责将航天器沿着跑道中心线进行直线平飞到达自动着陆段接口处。

1)捕获段设计

捕获段位于TAEM段的起始段，在捕获段阶段，航天器轨迹的地面投影与HAC的位置、最终半径和螺旋系数三个因素有关，为了使航天器飞行轨迹与HAC相切，倾侧角指令应与航向偏差角成正比。

υ=KvΔσAT

(3)

倾侧角的计算如式(3)所示。

ΔσAT是航天器当前的航迹偏角和与HAC相切所需的航迹偏角之间的偏差，Kv是比例系数，根据工程飞行试验得到的数据分析，工程最优取Kv值为3。

2)航向校准段设计

航向校准段飞行的目的是保证航天器沿HAC表面飞行，并控制动压和速度制动的变化。

(4)

航天器在沿着HAC柱表面飞行时要沿着HAC内旋的螺旋线进行航向修正，并使其最终对准跑道中心线。结合方程组(1)进行整合，得到航天器在航向校准段的飞行关系式如式(4)所示。

(5)

当航天器需要沿HAC柱进行飞行时，参考倾侧角的计算公式如式(5)所示。

(6)

为了使航天器更加精确地跟踪HAC柱的地面投影，将实际的倾侧角指令设为参考倾侧角的前馈输入与闭环反馈之和，如式(6)所示。

式(6)中ΔR是实际HAC半径与要求的HAC半径之差，KR和KRD均为比例系数，根据美国NASA公布的实际HAC计算数据，这2个系数分别设为0.02和10。

3)进场前飞行段设计

(7)

当航天器相对于跑道的航迹偏角小于5°时，即进入进场前飞行段，倾侧角指令切换为如式(7)所示。

式(7)中，y表示航天器的实际位置与跑道中心的横向偏差，Ky和KyD表示比例系数，根据美国NASA航天飞机多次返回任务过程实际测量得到的数据，这两个系数分别设为0.02和10.

υ≤υmax

(8)

在整个TAEM飞行段，倾侧角指令需满足式(8)的约束条件。

参考美国NASA公布的航天飞机返回过程TAEM段倾侧角指令约束范围，设υmax值为75°。

2.1.2纵向制导

在TAEM飞行阶段，航天器的飞行时间不能确定，而起始点与终点的飞行高度可以根据任务要求事先求知；并且由于在整个末端能量管理段，航天器在自身控制的飞行过程中绕HAC柱飞行的位移需要根据飞行器自身的能量进行调整。因此整个过程中航天器飞行所用的时间无法确定，因此时间无法作为自由变量。但是航天器在末端能量管理段飞行过程中的高度范围的可以确定的。因此整个控制过程使用飞行高度作为代替时间自由变量。

(9)

由于动压的数值很大，因此对误差的容忍能力也更大，速度的较小变化能引起动压的很大变化，而动压的较小变化对速度的影响较小。因此纵向制导设计选用跟踪动压-高度剖面，以实现对航天器速度的控制。使用如式(9)所示的三次多项式来定义需要跟踪的动压-高度剖面。

式(9)中，Q0、Q1、Q2和Q3是多项式的4个系数，可以由下列4个条件确定：

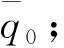
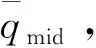
4)自动着陆段接口处的动压相对高度的变化率为0，如式(10)表示。

(10)

条件4可以确保在自动着陆段开始时，航天器在某一航迹倾斜角θALI飞行时处于“伪平衡”滑翔状态。此时动压保持在一个常值。

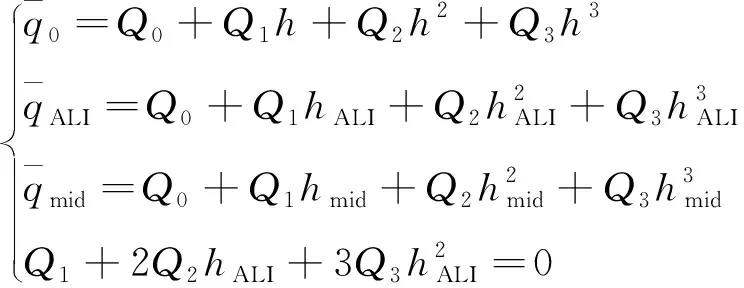
(11)

由以上4个条件建立方程组(11)。

由方程组(11)可以求得参考动压-高度剖面的4个系数Q0、Q1、Q2和Q3。因此纵向制导设计需要计算输入指令攻角α和航迹倾角θ的数据，确定参考动压-高度剖面

(12)

利用链式法则，计算动压相对于高度的导数如式(12)所示。

(13)

式(12)中，ρ为大气密度，ρ对高度求导如式(13)所示。

式(13)中，ρ0表示海平面大气密度，β表示大气标高的倒数。

结合方程组(1)，将式(13)与式(12)联立得式(14)。

(14)

将方程组第2式与第4式联立，得式(15)。

(15)

式(15)中，自变量由时间变为高度，得式(16)。

(16)

式(16)与(14)联立得方程组(17)，求解动压与动压变化率。

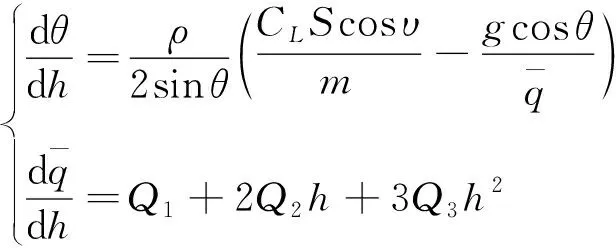
(17)

求解出参考动压-高度剖面4个系数和动压及其变化率后，结合式(3)、(5)、(6)、(7)可求解得到倾侧角指令υ后，通过求解方程组(17)得到控制变量攻角α和状态变量航迹倾角θ，从而确定参考动压-高度剖面，完成纵向制导设计。

2.2 迭代校正设计

TAEM段的轨道算法需要在迭代校正计算中不断进行航程调整，因此需要对运动方程进行数值积分，得到关于高度的方程组才能求解。

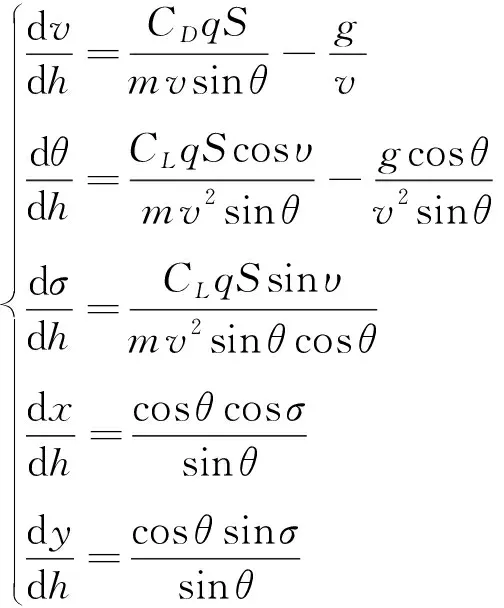
(18)

将方程组(1)中的第1，2，3，5，6式分别除以第4式，得到航天器的各状态变量相对于高度的微分方程组(18)。

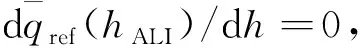
轨道算法首先根据TAEM段开始时航天器初始状态确定合适的进场方式。算法开始阶段默认选择间接进场方式，将HAC的最终半径设为最小，以及将HAC的地面位置设为最近(选择RF初始值为2500 m，xHAC=xALI)(xHAC为HAC的圆心位置，xALI为跑道中心线与实际位置的垂直距离)。二次螺旋系数R2为0.01。如果在上述最短航程的间接进场模式下，航天器的最终位置xf超过了自动着陆段接口处的位置xALI，则将航天器的进场方式确定为间接进场。

当航天器的最终位置xf没有超过自动着陆段接口处的位置xALI，则间接进场模式不可取。在这种情况下选择直接进场方式，此时依然选择最小的HAC半径及最近的HAC地面位置。如果在上述最短航程的直接进场模式下，航天器的最终位置xf超过了自动着陆段接口处的位置xALI，则将航天器的进场方式确定为直接进场。否则由于此时航天器离目标过远或者航天器的初始能量过低，不存在可行的TAEM段轨迹使航天器到达预定的自动着陆段并满足终端状态约束。图1表示的是航天器在TAEM段轨迹生成算法的流程。

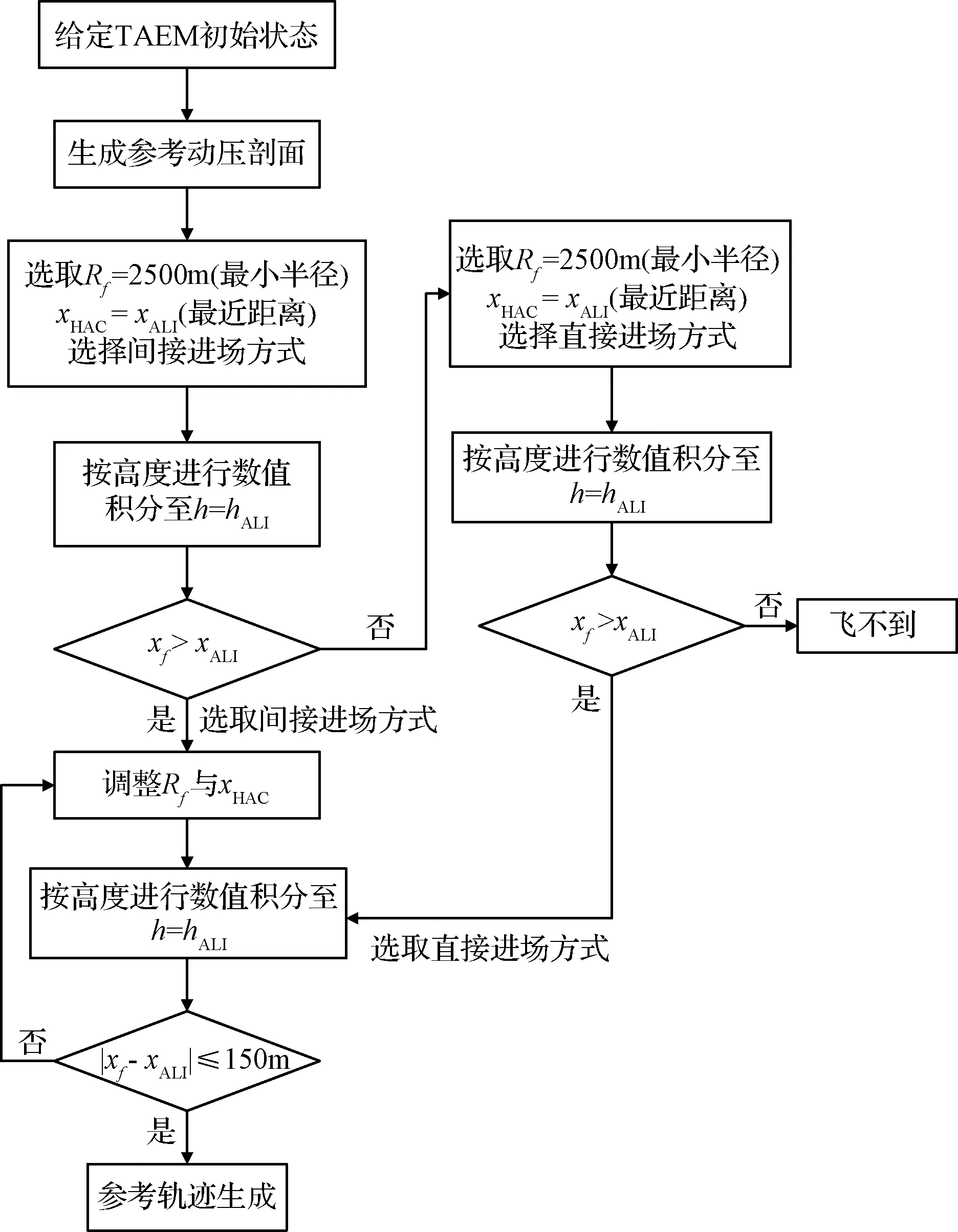
图1 TAEM段轨迹生成算法流程图Fig.1 The flow graph of TAEM orbit algorithm

在航天器进场方式确定之后，运行迭代校正算法，通过调整参数RF和xALI来调整航程和航天器在TAEM段末端的位置误差。

(19)

(20)

在每次的迭代过程中，最终的HAC半径由如式(20)所示的割线法确定。

(21)

式(21)中，ΔσHAC为HAC测量误差。

(22)

将式(22)与(21)相减得到式(23)。

(23)

然后计算HAC半径的方程如式(24)所示。

(24)

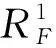
3 仿真校验

为验证该算法的有效性，以美国2011年5月16日奋进号航天飞机最后一次空间任务返回过程为仿真对象。大气模型采用1976年美国标准大气模型。奋进号航天飞机在进入TAEM段时高度、速度和航迹倾角状态变量分别为h0=30 000 m,v0=286 m/s,θ0=10°；其特征面积为S=249.9 m2；而在自动着陆段入口处的状态约束为hALI=3000±100 m,vALI=150±10 m/s,xALI=-8000±300 m。在奋进号航天飞机进入TAEM段接口时对位置和航迹偏角在大范围摄动的条件下进行一系列仿真计算，设航迹偏角的正方向为正北方向，具体计算结果详见表1。

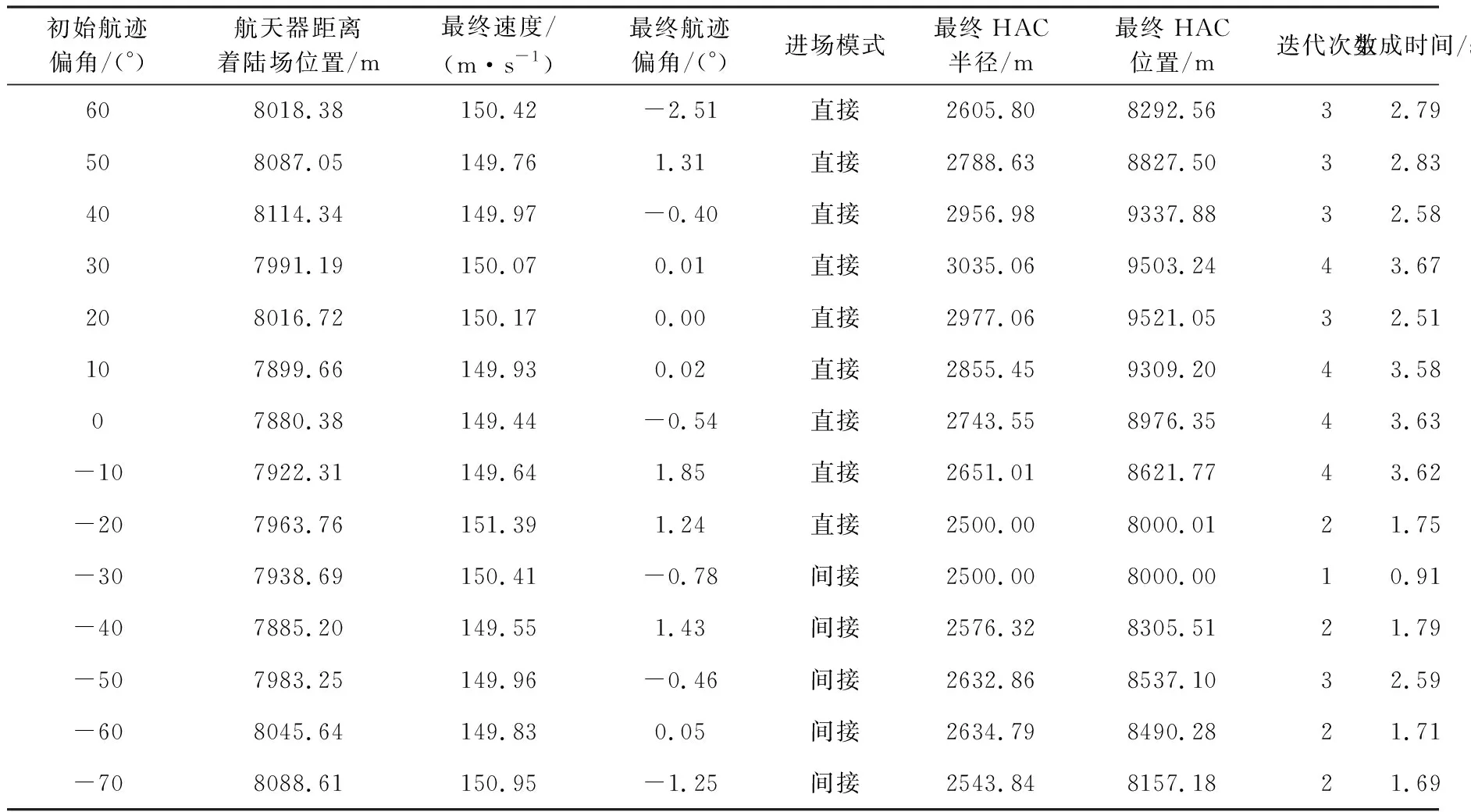
表1 位置与航迹偏角初始状态大范围摄动条件下的仿真结果Table 1 The simulation with large-scale perturbation and azimuth angle in initial position

从表1中可知，基于迭代校正的末端能量管理段轨道算法在进入TAEM段接口处时位置、航迹偏角存在大范围摄动情况下，仅迭代1～4次即可实现对轨道计算的收敛，成功生成TAEM段的飞行轨道，同时计算时间均控制在4 s以内。

将本文算法与奋进号返回时使用的TAEM段轨道算法(以下简称：原算法)同时应用在进入TAEM段接口时位置与航迹偏角均有大范围摄动情况下的仿真算例中，验证本文提出的轨道算法有效性。

在实际任务中，进入TAEM段接口时航迹偏角值为4.45°，此时奋进号与着陆场位置距离为7887.93 m。以表1中第3种情况为仿真算例进行验证，进入TAEM段接口时航迹偏角为40°，航天器与着陆场位置距离为8114.34 m。仿真结果如图2～图5所示。

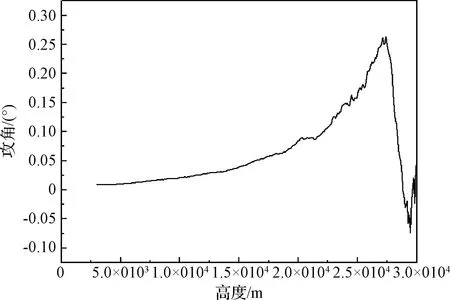
图2 高度-攻角关系剖面图Fig.2 Relationship with altitude and angle of attack

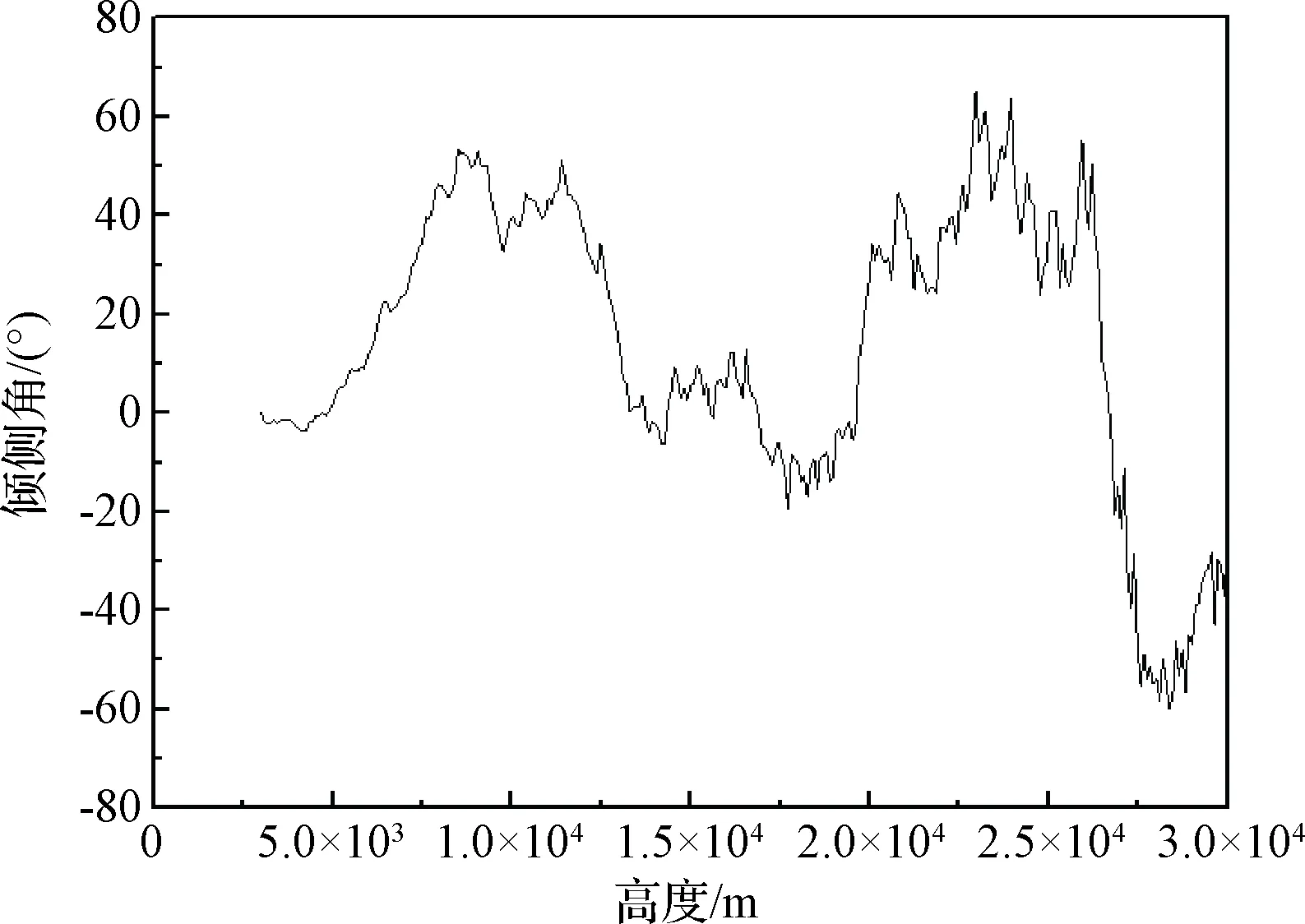
图3 高度-倾侧角关系剖面图Fig.3 Relationship with altitude and heel over angle

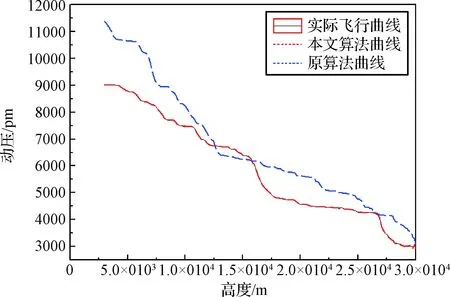
图4 高度-动压关系剖面图Fig.4 Relationship with altitude and dynamic stress

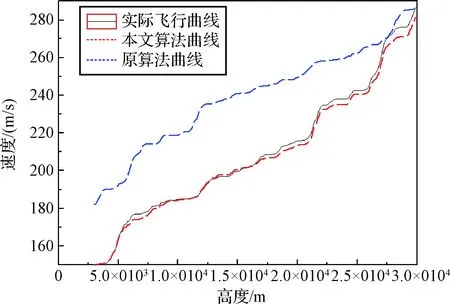
图5 高度-速度关系剖面图Fig.5 Relationship with altitude and velocity

图2表示的是由本文算法在仿真算例中生成的攻角变化曲线。在TAEM段初始阶段，攻角做较大机动配合飞行，经过一段距离的调整飞行后，攻角指令慢慢变小，同时开始捕获航向校准柱。当完成着陆阶段的航向校准后，控制指令指引的攻角指令逐渐减小为零。

图3表示的是由本文算法在仿真算例中生成的倾侧角变化曲线。在TAEM段初始阶段，航天器调整姿态进入接口处，然后通过调整完成着陆阶段的航向校准；在此过程中倾侧角通过较大变化配合机动飞行。在TAEM段终点处控制指令指引的倾侧角指令逐渐减小为零。

图4表示的是动压-高度变化曲线。黑色实线表示奋进号航天飞机在TAEM段时实际飞行时得到的动压-高度变化曲线；红色虚线表示在仿真算例下使用本文算法得到的动压-高度变化曲线；蓝色虚线表示在仿真算例下使用原算法得到的动压-高度变化曲线。

图5表示的是速度与高度的变化曲线。黑色实线表示奋进号航天飞机在TAEM段时实际飞行时得到的速度-高度变化曲线；红色虚线表示在仿真算例下使用本文算法得到的速度-高度变化曲线；蓝色虚线表示在仿真算例下使用原算法得到的速度-高度变化曲线。

图4中可以看出，本文算法生成的动压-高度关系曲线与实际飞行得到的曲线高度拟合。图5中，本文算法产生的速度-高度曲线虽然在开始阶段由于位置和航迹偏角大范围摄动而出现了小幅计算误差，但是在随后的仿真计算中显示了良好的鲁棒控制性能，得到的曲线与实际飞行的曲线基本保持一致。而当位置和航迹偏角发生大范围摄动时，原算法在进行TAEM轨道设计时无法进行有效的鲁棒控制，仿真计算的结果发生严重偏离，在TAEM段末端已经无法满足对自主着陆段的约束要求。仿真结果证明，在TAEM段接口处，当位置、航迹偏角有大范围摄动干扰时，本文的轨道算法可以成功生成参考轨道，同时满足自动着陆段的各种约束要求。

4 结 论

本文提出了一种基于迭代校正的TAEM段轨道算法，可以在TAEM段的初始的位置和航迹偏角存在大范围摄动条件下，快速生成可行的末端能量管理段轨道。通过跟踪轨迹投影实现侧向制导，通过跟踪动压-高度剖面实现纵向制导，使用HAC位置和最终半径调整轨道航程，使其在TAEM段初始状态存在位置、航迹偏角大范围摄动干扰下生成可行的飞行轨道。仿真试验证明，该算法在TAEM段的初始状态存在位置、航迹偏角大范围摄动情况下，可以自动选择进场方式，并生成满足自动着陆段接口处约束条件的飞行轨道。