基于子空间空间谱极值起伏特性加权的未知目标检测方法

陈建军， 郑恩明， 陈新华

(1.中国人民解放军91388部队, 广东 湛江 254002； 2.中国科学院声学研究所, 北京 100190)

在阵列信号处理中，目标检测与估计是一个重要分支[1-2]。当同一频带存在不等强度目标时，弱目标常常会被强目标所掩盖，针对同一频带不等强度未知目标检测问题，目前主要方法为阵元域预处理方法和波束域后置处理方法。现有阵元域预处理方法主要为零点约束法[3-4]、逆波束形成法[5]、阻塞法[6]、空域滤波法[7-8]、子空间法[9-18]等方法。该类方法主要通过信号处理手段在阵元域预先将强目标辐射信号滤除，然后再通过波束形成技术实现对其他未知目标的检测，但该过程需要事先预知哪些方位存在强目标等先验信息，以便从阵元域对强目标辐射信号进行滤除。当强目标与弱目标方位较近时，这些方法在滤除强目标辐射信号的同时也会削弱弱目标辐射信号，在一定方位区间下，不能有效实现对弱目标检测，存在一定探测盲区。或如子空间法，通过子空间重构法，实现对强目标子空间分离，但也存在如下问题：①根据设定较大特征值对应子空间为强目标子空间，存在强目标个数预先确定问题；②依据各子空间空间谱最大值位置的不同，通过判别最大值所在位置是否为强目标所在位置来判别强目标子空间，存在弱目标方位区间预先确知问题。

波束域后置处理方法主要是通过图像处理技术[19-20]对波束形成输出空间谱进行动态压缩或置零实现对弱目标检测。在谱值动态压缩法中，由于对波束形成输出空间谱进行了非线性变换，将会导致强目标对应空间谱形状发生变形，且也无法解决由于空间谱泄露而导致的弱目标淹没问题。强目标方位谱值置零同样也无法解决由于空间谱泄露而引起的弱目标淹没问题，且也无法解决不等强度目标在空间谱中的谱值差异问题。

针对同一频带中不等强度未知目标检测问题，本文依据不同目标辐射信号对各子空间空间谱贡献大小的不同，提出一种基于子空间空间谱极值起伏特性加权的未知目标检测方法。该方法利用各子空间空间谱极值起伏差异形成的加权因子对归一化的各子空间空间谱进行加权统计，可进一步抑制噪声子空间对最终空间谱的干扰，增强弱目标子空间空间谱，减小不同强度目标子空间空间谱幅值差异。无需事先预知目标个数和目标方位等先验信息，也无需通过构造判决因子实现对不等强度目标的判别和分离，只需估计出各子空间空间谱极值起伏特性的差异，即可在同一频带中对不等强度未知目标实现有效检测，并在同一波束图中清晰显示出相应检测结果。

本文接下来将探讨高斯噪声背景下，如何利用目标辐射信号对各子空间空间谱的贡献进行变换处理形成加权因子，解决同一频带中的不等强度未知目标检测问题，提高常规子空间重构法的鲁棒性和可检测性。

1 未知目标检测方法

1.1 常规波束形成方法

依据阵列信号处理理论，对于间距为d，阵元数为N元的等间隔水平线列阵，有I个不等强度目标从θi入射时，则第n个阵元接收频率wl数据Xn(wl)可表示为

(1)

式中：Si(Wl)为第i个目标辐射信号；Nn(wl)为第n个阵元接收的加性高斯白噪声频域数据；c为声速。

则线列阵各阵元接收数据频域矩阵形式可表示为

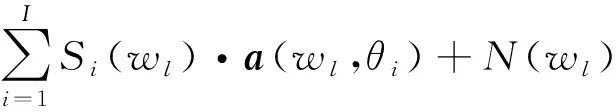
(2)

式中：a(wl,θi)=[1,ejwld cos θi/c，…,ejwl(N-1)d cos θi/c]T为第i个目标辐射信号阵列流形向量；[·]T为矩阵转置。N(wl)=[N1(wl),N2(wl),…,NN(wl)]T为各阵元接收噪声频域数据矩阵。

由线列阵各阵元接收频域数据所得的协方差矩阵R(wl)可以表示为

R(wl)=E{X(wl)XH(wl)}=RS(wl)+RN(wl)

(3)

式中：RS(wl)为目标频域数据协方差矩阵；RN(wl)为噪声频域数据协方差矩阵；[·]H为矩阵共扼转置。

则常规波束形成(Conventional Beam-Forming，CBF)所得空间谱可表示为

B(wl,θ)=WH(wl,θ)R(wl)W(wl,θ)

(4)

式中：W(wl,θ)=[1,ejwld cos θ/c，…，ejwl(N-1)d cos θ/c]T为波束形成加权因子；θ为波束形成预成方位角，一般取值为θ∈[0,Θ]，Θ=180。

1.2 基于子空间加权检测方法

以1.1节所示线列阵接收数据模型为基础，以频间非相干处理为例，对频率为wl的协方差矩阵R(wl)进行特征分解，可得

(5)

式中：λn(wl)和vn(wl)分别为R(wl)的第n个特征值及其对应特征向量。则第n个子空间空间谱为

Bn(w1,θ)=WH(wl,θ)Rn(wl)W(wl,θ)

(6)

式中：Rn(wl)=vn(wl)vn(wl)H为第n个子空间对应的子矩阵，将特征值λn(wk)省去，是为了进一步减小目标子空间空间谱幅值差异。

例如，对于一个间距为d=8 m，阵元数为N=4的线列阵，同时接收从θ1=40°和θ2=80°方向辐射来的频率为fc=80 Hz的非相干信号，目标1信号幅度为1，目标2信号幅度为0.1，对协方差矩阵R(wl)进行特征分解，所得特征值分别为λ1(wl)=1.0，λ2=(wl)=0.01，λ3(wl)=0，λ4=(wl)=0。由此可知，特征值λn(wl)代表为不同目标方差值，即目标1信号方差与λ1(wl)一致，目标2信号方差与λ2(wl)一致，由于只有两个目标，所以λ3(wl)和λ4(wl)没有对应目标对其做贡献，其值为0，不同目标对不同特征值贡献量不同。同时计算得到，子矩阵R1(wl)所有值的绝对值之和为4.0，子矩阵R2(wl)所有值的绝对值之和为3.94，两者输出空间谱幅值比由原先的|λ1(wl)R1(wl)|/|λ2(wl)×R2(wl)|≈101变为现在的|R1(wl)|/|R2(wl)|≈1.01。所以，在求取各子空间相应子矩阵时，将特征值λn(wl)省去，可以进一步减小目标子空间输出空间谱幅值的差异。

Bn(wl,θ)体现了线列阵接收数据在θ方位处对第n个子空间的贡献，即空间不同目标对每个子空间的贡献可以用式(6)所示空间谱表示。因此，可通过构造相应加权因子重新配置不同子空间空间谱在最终空间谱的比例，进而达到削弱噪声和强目标子空间空间谱对弱目标子空间空间谱干扰，增大弱目标子空间空间谱在最终空间谱中的比例，在同一频带中对不等强度未知目标实现有效检测，并在同一波束图中清晰显示出相应检测结果。

若采用常规子空间重构法对目标实现检测，则最终空间谱可表示为

(7)

当目标辐射信号只占据某一个或某几个子空间时，则式(7)会将所有子空间空间谱等价地加权到最终空间谱中，由于噪声所占用子空间较多、强目标子空间空间谱幅值较大，此式所得最终空间谱受噪声和强目标子空间空间谱影响较大，不便于对弱目标实现有效检测。为此，可在式(7)的基础上，采用相应处理来改变各子空间空间谱在最终空间谱中的比例，以削弱噪声与强目标子空间空间谱对弱目标子空间空间谱的干扰，则式(7)可变换为

(8)

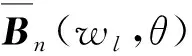
图1 波束形成极大值及其位置示意图Fig.1 Schematic diagram of maximum value and position of beamforming

依据图 2所示流程图，本算法实现过程可分为以下几个步骤：

步骤1对线列阵各阵元拾取离散信号xn(mTs)，1≤n≤N，Ts为采样间隔，然后按式(9)做FFT(Fast Transform Algorithm)，可得到各阵元拾取数据的频域数据。

(9)

式中：wl=2πl/MTs为FFT分析中的第wl频率单元，1≤m≤M为FFT变换采样点数。

步骤2对频率为wl的协方差矩阵R(wl)进行特征分解，求取第n个子空间对应子矩阵Rn(wl)，由子矩阵按式(6)得到第n个子空间空间谱Bn(wl,θ)，n=1,…,N。

步骤3如图 1所示，对每一个子空间空间谱求取极大值，则主极大值位置为该子空间空间谱的主瓣位置，其他次极大值位置为子空间空间谱的旁瓣位置，分别记为θn,main与θn,side，n=1,...,N。

步骤4提取子空间空间谱极大值，然后按式(11)形成加权因子。

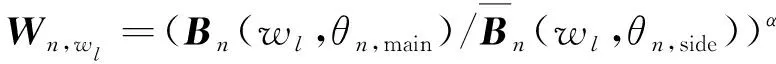
(10)

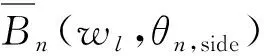
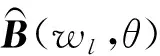
1.3 基于子空间加权检测方法分析

以频率wl处理为例， 假定各阵元接收信号中包含两个不等强度的未知目标，两个目标辐射信号各占协方差矩阵中的一个子空间，其他子空间为噪声子空间。则目标信号子空间空间谱Bn(wl,θ)|n=1,2可近似表示为

(11)

图2 基于子空间空间谱极值起伏特性加权的检测方法流程图Fig. 2 Schematic diagram of detection method based on the extremum fluctuation feature of the subspace spatial spectrum for unknown target

式(11)为sinx/x形式的函数，则第一次极大值为0.22，其他次极大值小于0.22，所以主极大值与次极大值比大于1/0.22。经过优化处理后，目标子空间空间谱的旁瓣级可进一步得到抑制，主极大值与次极大值将比得到进一步扩大，最后的加权因子远大于1/0.22，即Wn,wl|n=1,2> >1/0.22。

由图 3和图 4可知，目标子空间主极大值与次极大值之差为20 dB，目标子空间的加权因子Wn,wl|n=1,2> >1/0.22。

图3 弱目标子空间空间谱(t=70 s)Fig. 3 Spatial spectrum of weak target subspace (t=70 s)

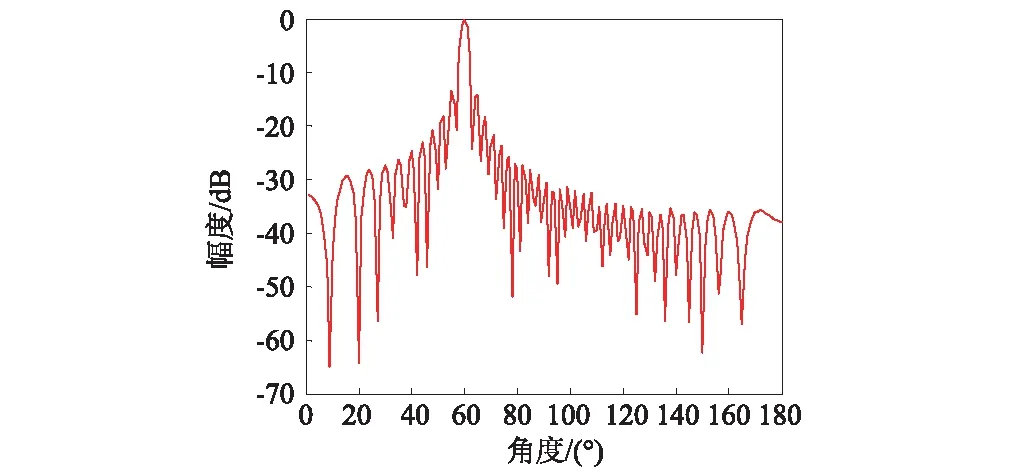
图4 强目标子空间空间谱(t=70 s)Fig.4 Spatial spectrum of strong target subspace (t=70 s)

而其他噪声子空间空间谱Bn(wl,θ)|n≠1,2不再是具有sinx/x形式的函数，而是与噪声一样，空间谱各位置的幅值是随机的，主极大值与次极大值的差别较小，加权因子较小Wn,wl|n≠1,2≈1。

由图 5可知，噪声子空间主极大值与次极大值相似，近似无差别。

图5 噪声子空间空间谱(t=70 s)Fig.5 Spatial spectrum of noise subspace (t=70 s)

另外，从波束形成系统的直流响应[21-22]方面分析也可知，目标子空间空间谱对准目标方位波束的直流输出的理想值为

(12)

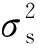
目标子空间空间谱没有对准目标方位波束的理想值为

(13)

两者之差为目标子空间对准目标方位时的直流跳变，即主极大值与次极大值的差值为

(14)

同样，噪声子空间由于没有目标信号，其空间谱所有方位波束的理想值为

(15)

则噪声子空间主极大值与次极大值的差值为

(16)

由式(14)和 式(16)可知，目标信号子空间空间谱主极大值与次极大值之差远大于噪声子空间空间谱主极大值与次极大值之差。

通过求取各子空间主极大值与次极大值比值形成加权因子，则式(7)将变为

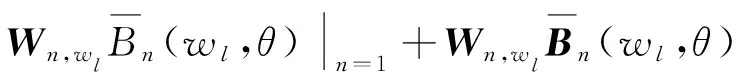
(17)

图 6～图 9 为CBF(Conventional Beam-forming)、常规子空间重构法、本文方法所得空间谱和方位历程图。

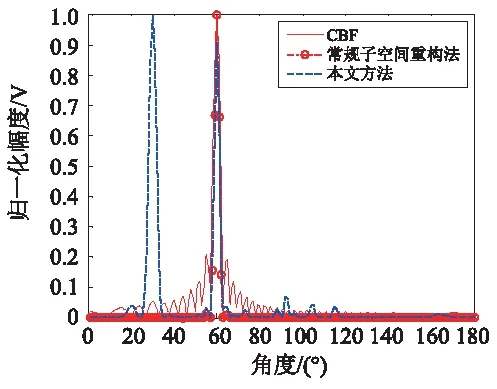
图6 不同方法所得空间谱(t=10 s)Fig. 6 Spatial spectrum by different methods (t=10 s)

图7 CBF所得方位历程图Fig.7 Bearing/time record of CBF

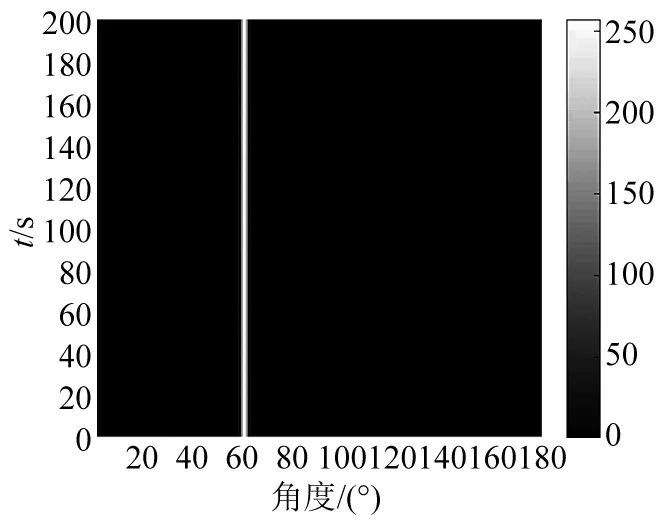
图8 常规子空间重构法所得方位历程图Fig.8 Bearing/time record of conventional subspace reconstruction method

图9 本文方法所得方位历程图Fig. 9 Bearing/time record of this method

由图 6～ 图 9 可知，CBF和常规子空间重构法已经无法实现对弱目标的有效检测，而经过子空间空间谱主极大值与次极大值比加权的波束形成可以很好对不等强度未知目标实现有效检测，且目标检测效果与子空间空谱所示结果相近。由图 10可知，Wn,wl|n=1≈Wn,wl|n=2>>Wn,wl|n≠1,2，联合式(17)可得本文方法所得最终空间谱类似于只由目标子空间谱加权拟合而得，且无需事先预知目标个数和目标方位等先验信息，也无需通过构造判决因子实现对不等强度目标的判别和分离，只需估计出各子空间空间谱极值起伏差异，即可依据不同子空间空间谱极值起伏特性的不同，削弱了噪声子空间与强目标子空间对弱目标子空间空间谱的干扰，增大弱目标子空间空间谱在最终空间谱中的比例，在同一频带中对不等强度未知目标实现有效检测，并在同一波束图中清晰显示出相应检测结果。

另外，由仿真数据统计平均得到，采用本文方法相比CBF、常规子空间重构法，弱目标子空间空间谱在最终空间谱的比例由原先的0.31%变为现在的48.89%，理论推导值为50%；强、弱目标子空间空间谱幅值比由原先的316变为现在的1.046，数值仿真结果与理论分析相符合。

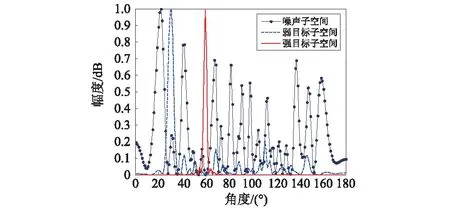
图10 典型子空间空间谱(t=10 s)Fig.10 Beam map of typical sub-covariance matrix (t=10 s)

图3～图10的仿真条件如下：不等强度目标辐射信号中心频率为fc=60 Hz，背景噪声带宽为f=40～80 Hz，强目标相对线列阵方位角为θ=60°，弱目标相对线列阵方位角为θ=20°∶ 220°(@t=0 ∶ 200 s)，强目标辐射信号和弱目标辐射信号谱级比为SLR=25 dB，弱目标辐射信号与背景噪声信噪比为SNR=-20 dB；线列阵相邻阵元间距为d=8 m，阵元数为N=64，声速为c=1 500 m/s，采样率为fs=5 000 Hz，一帧数据长度为T=1 s，样本有效率为100%。图 3～图10所示结果是按CBF、常规子空间重构法、本文方法对采集数据中的fc=60 Hz频率单元进行波束形成所得，在求取Wn,wl时，α=2。

2 实测数据处理

本次实测数据为进行某次目标检测试验所得。试验采用32元水平线列阵接收信号，阵元间隔为8 m，线列阵尾端方向为180°。

实测数据实例1：本次实测数据处理长度为300 s，所用采样率为fs=5 kHz，图 11～图 14所示结果是按CBF、常规子空间重构法、本文方法对线列阵接收信号数据中的fc=67 Hz频率单元进行波束形成所得，在求取Wn,wl时，α=2。

由图 11～图 14可知，采用本文方法除了能够清晰显示出该频带内存在5个目标，目标方位分别为：51°，60°～120°，77°，85°和106°，好于CBF、常规子空间重构法对77°，85°和106°处目标检测效果。该结果与式(17)分析结果相符合，证实了本文方法能对同一频带中的不等强度未知目标实现有效检测，并在同一波束图中连续显示出对未知目标的检测结果和方位。

实测数据实例2：本次实测数据处理长度为400 s，所用采样率为fs=5 kHz，图15～图18所示结果是按CBF、常规子空间重构法、本文方法对线列阵接收信号数据中的fc=78 Hz频率单元进行波束形成所得，在求取Wn,wl时，α=2。

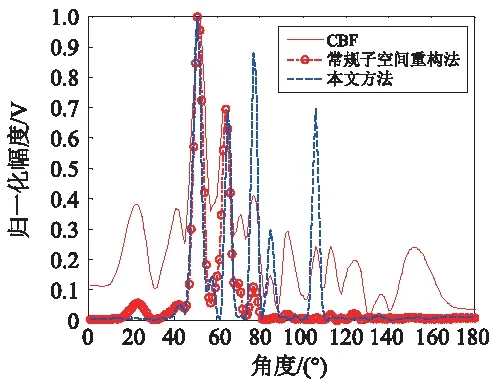
图11 不同方法所得空间谱(t=10 s)Fig.11 Spatial spectrum by different methods (t=10 s)

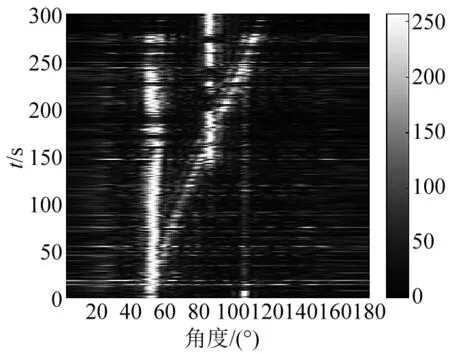
图12 CBF所得方位历程图Fig.12 Bearing/time record of CBF

图13 常规子空间重构法所得方位历程图Fig.13 Bearing/time record of conventional subspace reconstruction method

图14 本文方法所得方位历程图Fig.14 Bearing/time record of this method

图15 不同方法所得空间谱(t=330 s)Fig.15 Spatial spectrum by different methods (t=330 s)

图16 CBF所得方位历程图Fig.16 Bearing/time record of CBF

图17 常规子空间重构法所得方位历程图Fig.17 Bearing/time record of conventional subspace reconstruction method

图18 本文方法所得方位历程图Fig.18 Bearing/time record of this method

由图15～图18可知，采用本文方法除了能够显示70°～90°内的两个强目标，还能清晰地显示100°附近的弱目标，好于CBF、常规子空间重构法对不等强度目标检测效果。该结果与式(17)分析结果相符合，同样证实了本文方法能对同一频带中的不等强度未知目标实现有效检测，并在同一波束图中清晰显示出对未知目标的检测结果和方位。

4 结 论

依据不同目标辐射信号对各子空间空间谱贡献大小的不同(如图3～图5所示)，本文通过构造合适的加权因子重新配置了各子空间空间谱在最终空间谱中的比例，以削弱噪声与强目标对弱目标干扰，并对各子空间空间谱进行归一化处理，进一步降低强目标子空间对弱目标子空间的干扰，减小不同强度目标子空间空间谱幅值差异，增强弱目标子空间空间谱在最终空间谱的比例。依据分析和数值仿真结果，本文提出一种基于子空间空间谱极值起伏特性加权的未知目标方法。

本文方法利用各子空间空间谱极值起伏特性的不同，对各子空间空间谱进行不等权值加权，在本文数值仿真条件，本文方法使弱目标子空间空间谱在最终空间谱的比例由原先的0.31%变为现在的48.89%，理论推导值为50%；强、弱目标子空间空间谱幅值比由原先的316变为现在的1.046，提升了弱目标子空间空间谱在最终空间谱的比例，降低了强、弱目标子空间空间谱幅值在最终空间谱中的差异，相比CBF、常规子空间重构方法，在无先验信息情况下，对同一频带中的不等强度未知目标在同一波束图中实现了有效检测和显示。另外，实测数据处理结果也进一步验证了：相比CBF、常规子空间重构方法，本文方法改善了CBF和常规子空间重构法对同一频带中不等强度未知目标的检测性能，并在同一波束图中，同时对不等强度未知目标实现有效检测。