多档导线面内动态特性及共振条件分析
2018-09-28刘小会蔡萌琦
刘小会, 胡 友, 严 波, 蔡萌琦
(1.重庆交通大学 土木工程学院,重庆 400074; 2.重庆大学 航空航天学院,重庆 400044;3. 成都大学 建筑与土木工程学院,成都 610106)
高压输电塔线体系作为国家经济建设的生命线工程,它的正常运行保证了国家经济发展。由于舞动、脱冰会导致输电线断线等事故,因此针对架空输电线的非线性动力响应研究具有重要的理论意义和工程实际价值。
导线的动力响应与索振动理论密切相关,Irvine等[1]针对孤立单跨索的模态和频率进行了研究,得到单档导线无量纲固有频率随几何参数变化关系。Rega等[2-4]在Irvine等的基础上详细分析了悬索产生共振的条件,并且根据单跨索的理论模态和频率提出了悬索的非线性振动理论,得到了索振动幅值和固有频率之间的关系,并且发现了很多分岔现象。Luongo等[5-6]提出了风载荷作用下考虑弯曲刚度的弹性曲梁模型,利用摄动法对具有初始挠度的导线进行非线性动力响应分析。Desai等[7]应用索振动理论对单跨覆冰导线控制方程进行Galerkin离散,研究覆冰导线气动稳定性及动力响应 。现有的对覆冰输电线舞动理论分析主要基于单档导线,实际高压输电线路是由多跨导线构成,其中悬垂绝缘子串顺线路方向偏转会导致相邻两档导线相互影响,而有限元分析结果指出多跨导线之间相互影响不容忽略[8-10],仅仅考虑单档导线舞动或将相邻档导线的影响等效为弹簧约束[11-13]是不能满足工程需求。因此,多跨导线模态及频率的研究对于连续档导线非线性动力响应的理论分析具有重要意义。最近王磊[14]采用有限元方法研究了塔线耦合体系的模态及频率, Xie等[15]研究了档距比对两档导线频率的影响,Yi等[16]建立了中部为滑轮约束的三跨索在悬挂重物情况下的自由振动模型,并基于该模型研究了重物质量对振动频率的影响。虽然对多跨索的振动频率取得了一定的研究成果,但是在不同地区实际输电线路的档数、档距比、导线张力等线路结构参数均不相同,因此对于输电线路模态和频率还需进一步的深入研究。
本文获得连续档导线面内振动的固有频率理论公式,利用该公式详细分析了不同档数的连续档导线产生共振的条件;基于模态综合法获得连续档导线的模态函数,详细分析了连续档导线模态的构成,以及能够产生耦合振动的连续档导线模态,为连续档导线非线性动力响应分析奠定了理论基础。
1 两档导线动态特性分析
1.1 两档导线精确模态计算
建立考虑绝缘子串的两档导线力学模型,如图1所示。l1为第一档导线档距;l2为第二档导线档距;H为导线自重作用下静止时的水平张力。Tr1,Tl2分别为AB及BC档导线对绝缘子串向下的拉力;a为绝缘子串长度。在外部载荷影响下导线由虚线位置移动到实线位置(见图1),绝缘子串端部B向左移动到B′点,移动水平距离为Δx。此时AB档导线水平张力变化量为hτ1,BC档导线水平张力变化量为hτ2。将两档导线中的每一档导线视为子结构,任意一档导线面内运动方程均可描述为

图1 两档导线Fig.1 Two-span conductor
(1a)
(1b)
式中:H为导线静止时的水平张力;hτ为导线运动时水平张力的变化量;m为导线单位长度的质量;c为阻尼系数;w为导线面内竖向位移;u为沿导线弦向的水平位移。x为导线弦向坐标(见图1),y为导线静止时竖向的坐标,当小弧垂时可近似采用抛物线公式描述导线静止时构形
(2)
考虑到静态水平张力H为常数,当弧垂较小时可认为ds≈dx,化简并消去高阶小量可得
(3a)
(3b)
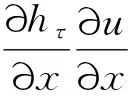
(4)
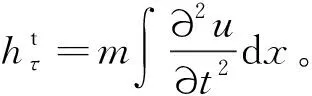
(5)
式中:Le为导线的线长。如果两档导线端部有位移,则根据叠加法得到导线任意一点的位移为
w(x,t)=w(0,t)+[w(l,t)-w(0,t)](x/l)+wt(x,t)
(6a)
u(x,t)=u(0,t)+[u(l,t)-u(0,t)](x/l)+ut(x,t)
(6b)
式中:wt(x,t)和ut(x,t)为非端部运动引起的导线位移。令第一档导线的位移为w1(x,t),u1(x,t);第二档导线的位移为w2(x,t),u2(x,t)。根据两档导线位移的边界条件,代入式(6)可得
u1(x,t)=-Δx(x/l1)+ut1(x,t)
(7a)
u2(x,t)=-Δx(1-x/l2)+ut2(x,t)
(7b)
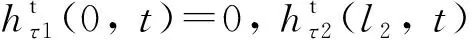
(8a)
(8b)
将式(8)和式(4)代入式(3a)可得
(9a)
(9b)
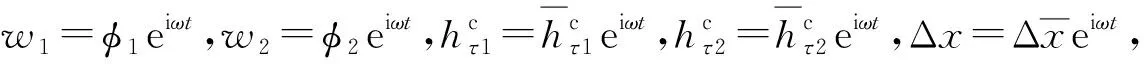
(10a)
(10b)
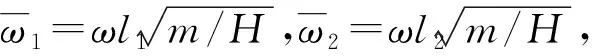
(11a)
(11b)
将边界条件φ1(0)=φ2(0)=0,φ1(l1)=φ2(l2)=0代入式(11),可求解部分系数,再将式(11)代入式(10)可求解所有系数,最终得到式(10)的解为
(12a)
(12b)
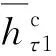
(13a)
(13b)
式中:λ1,λ2,K1和K2分别为
(14a)
(14b)
将式(13)代入式(12)中可得理论模态函数
(15a)
(15b)
式中:C1与C2分别为
(16a)
(16b)
由Irvine等的结论可知孤立档导线的模态函数有两种形式,对称模态与反对称模态,分别表示为
(17)

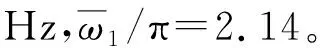
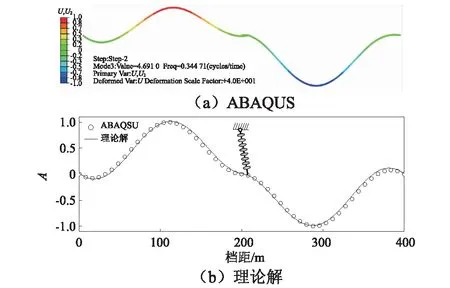
图2 200~200 m导线模态对比Fig.2 Mode contrast of 200-200 m conductors
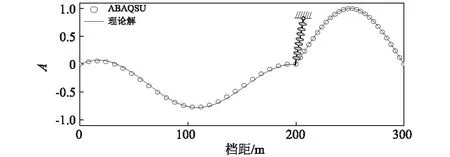
图3 200 ~100 m导线模态对比(a=0.2 m)Fig.3 Mode contrast of 200-100 m conductors(a=0.2 m)

图4 200~100 m导线模态对比(a=0.5 m)Fig.4 Modes contrast of 200-100 m conductors(a=0.5 m)
1.2 两档导线频率精确计算
如需得到两档导线频率的理论计算公式,还需要补充一个方程。针对图1中绝缘子串列力矩平衡方程
hτ1a=(Tl2+Tr1)Δx+hτ2a
(18)
式中:Tr1与Tl2分别为AB档及BC档导线对绝缘子串下端的拉力。如果应用式(8)求解式(18),则求解很困难。为了能够容易得到相对准确的理论解,忽略小量,将式(8)进行简化,最后得到简化后的张力增量为
(19)
将式(19)代入式(18)可得
(20)
(21)
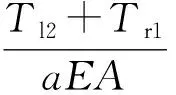
(22)
如果绝缘子串长度趋于零,可认为绝缘子串对导线的约束为固定铰约束,此时两档导线的频率与模态均独立,互不相干。根据式(22)可知,这两个公式可以分别计算两档导线的频率,与Irvine等得到的单档导线的频率计算公式相同。
实际上绝缘子串长度既不为零,也不是无穷大,因此需要对式(20)进行求解。消去式(20)的分母可得
(23)
求解式(23)可得
(24)
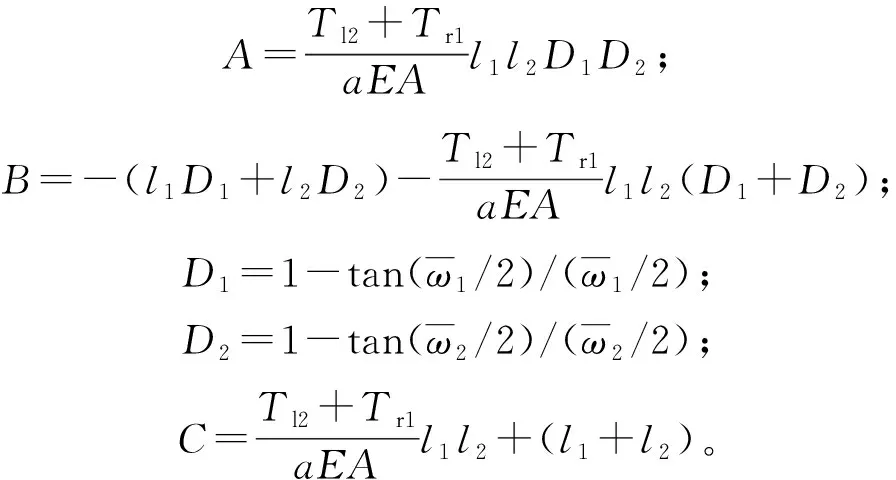

图5 绝缘子串长度对第一阶模态频率的影响Fig.5 Effect of natural frequenciesfor first mode on insulator string length
当绝缘子串长度超过1 m时,绝缘子串长度变化对频率的影响减弱,因此对于绝缘子串长度较长且导线张力较大的高压输电线路,其频率的计算公式可以采用简化式(21)计算,如果线路张力较小且绝缘子串长度较短则需要采用精确式(23)。实际上大部分的高压输电线路绝缘子串长度大于1 m,而且对于500 kV超高压输电线路绝缘子串长度可以达到4~5 m,所以对于高压输电线路可以采用简化公式计算其频率。
1.3 两档导线模态及频率的简化计算

(25)
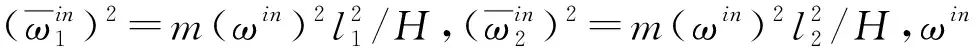
建立档距为100~110 m,绝缘子串长度为2.25 m的220 kV高压输电线路有限元模型,绝缘子长度与实际情况相同,其它材料参数与上例相同。当张力H为4.8 kN (λ1/π=10)时,通过ABAQUS获得的模态ψ11,ψ21和ψ23的形式,如图6中的散点所示。将相应的参数代入式(25)可以得到理论模态,如图6中的实线所示。两者吻合。这说明绝缘子串较长且张力较小时近似式(25)能够较好的描述两档导线的对称模态。

图6 两档导线面内对称模态Fig.6 In-plane symmetrical modes of two spans conductors
通过H为4.8 kN(λ1/π=10)的有限元模型还得到两档导线另外一类反对称模态,如图7中的散点所示。模态ψ22表示第二档导线为两个半波的反对称模态,而第一档导线无模态位移。模态ψ12为第一档导线为两个半波的反对称模态,第二档导线的模态位移也为零,对于反对称模态两档导线之间是独立的,互不影响,这些特点与对称模态不同。究其原因是因为反对称模态不会引起Irvine等提出的导线线性动张力,也不会使的绝缘子串产生顺线路方向的偏转,所以对于反对称模态相邻档之间的导线是独立的。
根据式(15)的特点,去掉其对称部分,只保留反对称部分,两档导线的反对称模态可以表示为
(26)
式中:下标i为模态主要以i跨为主;n为模态的半波个数,式(26)只适合n为偶数情况。当i=j时δij为1,当i≠j时δij为零。i和n取不同值时代入式(26)可得两档导线反对称模态,将相应的参数代入式(26),得到两档导线反对称理论模态,如图7中的实线所示,对比可以看出有限元计算结果和式(26)非常吻合。图7中的三个反对称模态均表明,当其中一档振形有偶数半波时,另外一档的位移为零,这说明两档导线的模态是相互独立的,根据Irvine等的理论可以通过反对称模态式(26)满足边界条件来确定相应的频率,得到的无量纲频率不随几何参数改变,为水平直线。
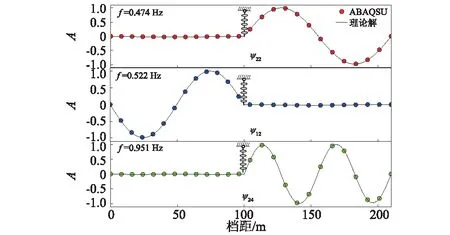
图7 两档面内反对称模态Fig.7 In-plane asymmetric modes of two spans conductors
前文得到了形式复杂的频率理论计算公式,见式(20)。该公式是一个超越方程,仅仅对于两档导线其计算量也非常大,且不宜推广到任意档导线。考虑到实际的高压输电线路绝缘子串长度较长,且张力大,可采用简化式(21)。而采用简化式(21)很容易推广到任意档导线,下面对任意档频率计算进行简单推广。对于任意N档导线,如图8所示。
根据式(19)及两端耐张档的边界条件可知连续档导线的动态张力增加量为

图8 N档导线Fig.8 N span conductor
(27)
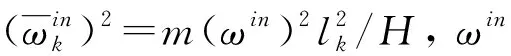
(28)
(29)
如果线路的结构参数是确定的,则式(29)中只有一个未知量ωin,依据式(29)可以计算任意连续档导线对称模态对应的频率,这里对称性与反对称性均针对连续档导线中单档导线的振形而言。

图9中曲线和纵坐标相交λ2/π时为零,式(29)右边为无穷大,可得
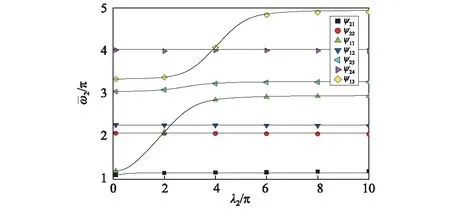
图9 两档导线自振频率Fig.9 Natural frequencies of two spans conductors
(30a)
(30b)

改变导线最低点张力时,通过ABAQUS获得的反对称模态对应的无量纲频率和几何参数变化关系见图9中散点,模态ψ22和ψ12的无量纲频率几乎不随几何参数变化,与孤立档导线的频率变化特征相同(见图9)。考虑到两档导线反对称模态和无量纲频率的特点,可以认为连续档导线出现反对称模态时频率的计算方法和孤立的单档导线相同
(31)
式中:li为对应档的档距;n为模态的半波个数,取偶数值。
2 多档导线面内频率及模态分析
2.1 三档导线面内模态及频率计算
在ABAQUS软件中建立三档导线的有限元模型,档距分别为100 m,130 m和170 m。导线最低点张力为11.9 kN(λ3/π=4),导线和绝缘子串的材料性质与前文相同。通过有限元方法获得的三档导线面内对称模态,如图10(a)中散点所示。导线张力对模态形状有明显影响,如将导线最低点张力改为18.8 kN(λ3/π=2)时,这三种模态的散点图,如图10(b)所示。对比两图可以看出张力变化对前三阶对称模态的形状有显著影响。
依据前文理论将三档导线视为三个子结构,每一个子结构的模态根据前文理论结果获得,推广到三档导线可以得到简化的对称模态理论公式
(32)
将相应的线路参数代入式(32)可以获得三档导线的三个对称低阶模态ψ11,ψ21和ψ31,如图10实线所示。从图10(a)可知,当导线最低点张力为11.9 kN(λ3/π=4)时,采用理论方法获得的第一阶对称模态曲线与有限元结果有明显差别,但是后两阶对称模态基本吻合。当导线最低点张力增大到18.8 kN(λ3/π=2)时,第一个对称模态的理论曲线和有限元结果吻和较好,且其它两个低阶对称模态也较为吻合。
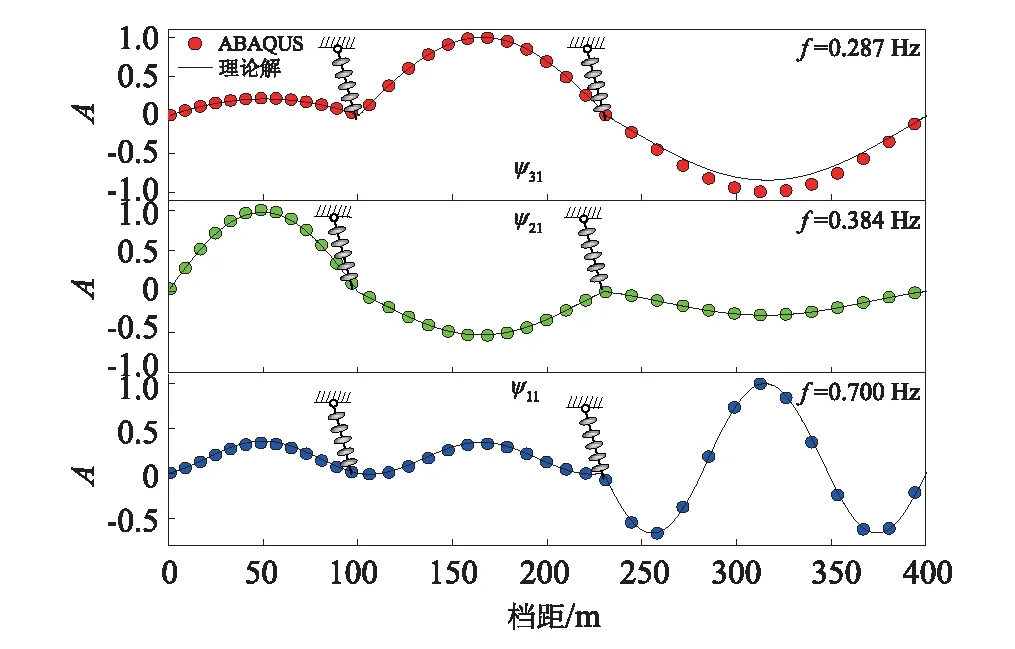
(a) H=11.9 kN(λ3/π=4)
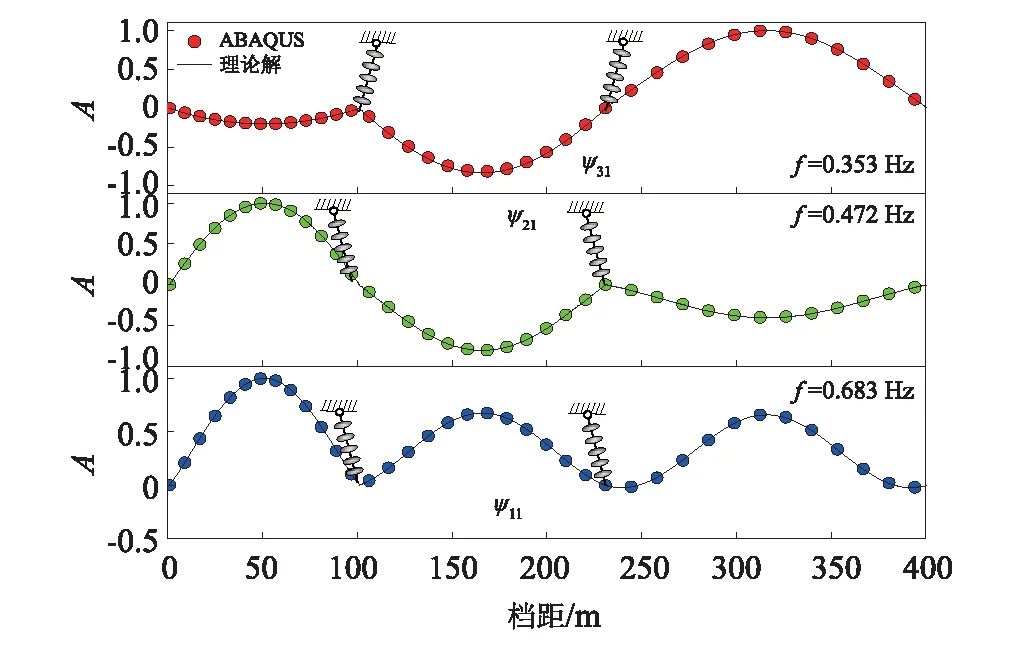
(b) H=18.8 kN(λ3/π=2)图10 三档导线面内对称模态Fig.10 In-plane symmetric modes of three spans conductors
当张力较小时(见图10),采用式(32)描述第一阶对称模态与真实结果有较明显的误差,但是对于高阶对称模态则能够吻合较好。以220 kV高压输电线为例,其常用导线型号为LGJ-300或LGJ-400的钢芯铝绞线,其导线计算拉断力范围约为68~171 kN,如果按照2.5的安全系数,其导线的实际拉力设计值可达27~68 kN,大于18.8 kN(λ3/π=2)。根据图10(b)中的对比情况可知,采用简化式(32)也可以与实际情况吻合较好。考虑到实际线路拉力的设计值较大,所以理论分析高压输电线路模态时可以采用简化式(32)。这里值得一提的是,档距增加时相同的λ/π对应不同的导线张力。例如对于档距为400 m的导线,λ/π为2时对应导线最低点张力为33.3 kN,而λ/π为4时对应导线最低点张力为21.0 kN。
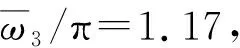

图11 三档导线自振频率Fig.11 Natural frequencies of three spans conductors
2.2 四档导线面内模态及频率分析
建立四档导线有限元模型,档距从左到右依次为100 m,130 m,150 m和170 m,导线的最低点张力为18.8 kN(λ4/π=2),导线和绝缘子串的材料性质和前文相同,绝缘子串的长度仍为2.25 m。通过ABAQUS有限元软件获得的四档导线对称模态如图12中的散点,四档导线的四个低阶对称模态ψ11,ψ21,ψ31和ψ41是由单档导线的对称模态组合而成。将式(32)推广可以获得四档导线的模态函数,将对应参数代入即可得四档导线的理论模态,如图12中的实线所示。对比可以看出理论结果和有限元结果吻合。观察这四个模态还可以看出,档距接近的导线其模态位移也较为接近,如模态ψ41的三档和四档导线模态位移均远大于第一档和第二档。
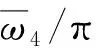
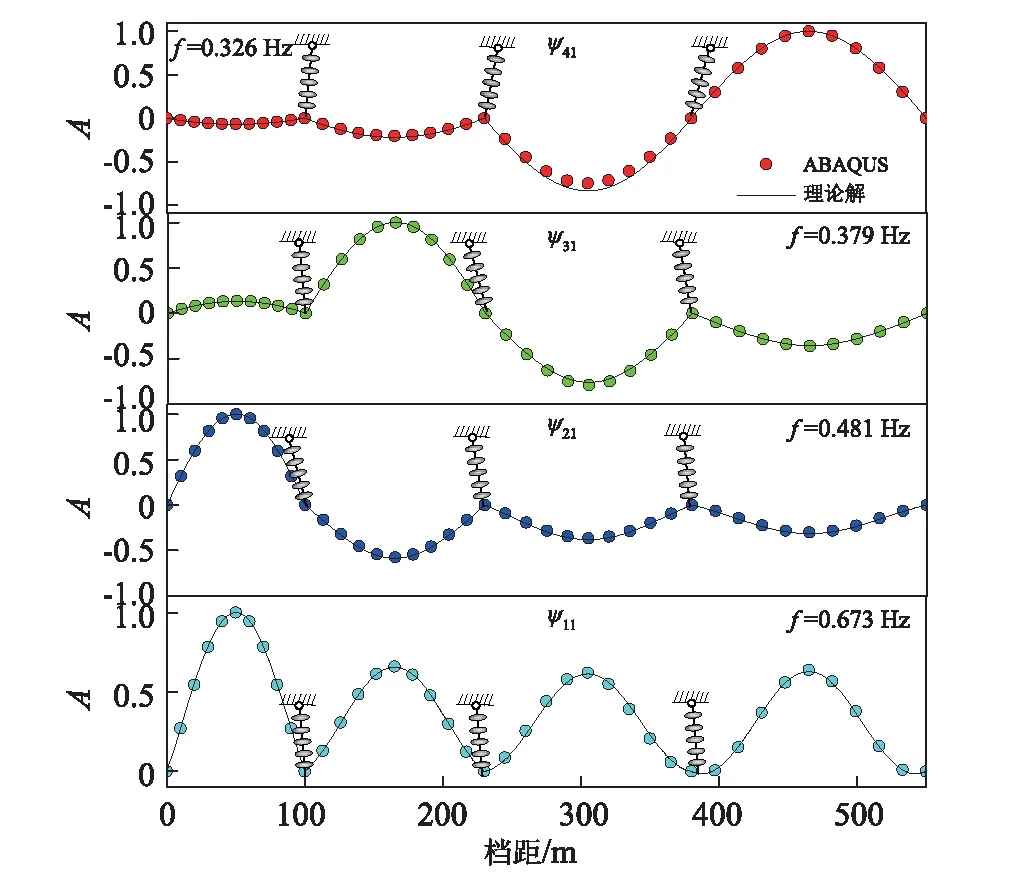
图12 四档导线面内对称模态Fig.12 In-plane symmetric modes of fore spans conductors

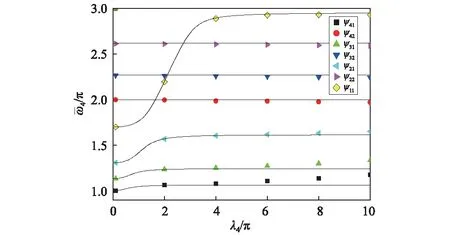
图13 四跨导线面内自振频率Fig.13 Natural frequencies of fore spans conductors
2.3 五档导线面内模态及频率分析
建立五档输电线路的有限元模型,从左到右档距依次为100 m,110 m,130 m,150 m和170 m,导线的最低点张力为18.8 kN(λ5/π=2),绝缘子串长度为2.25 m,导线和绝缘子串的材料性质与前文相同。将相应的参数代入ABAQUS中即可获得其模态,如图14散点所示,该五个模态由单档为半个波的对称模态组合而成。将式(32)推广可以获得五档导线的模态函数,将对应参数代入即可得到五档导线的理论模态,如图14中的实线所示。对比可知理论结果和有限元结果吻合。

图14 五档导线面内对称模态Fig.14 In-plane symmetric modes of five spans conductors

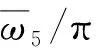

图15 五档导线自振频率Fig.15 Natural frequencies of five spans conductors
2.4 连续档导线模型化简
上文获得的连续档导线对称模态与反对称模态具有正交性,这里对正交性不予证明,仅给出简化运动控制方程的关键结果。现将称模态的模态函数对x求导,当n和k都为奇数时两不同模态的乘积沿导线长度方向积分可得
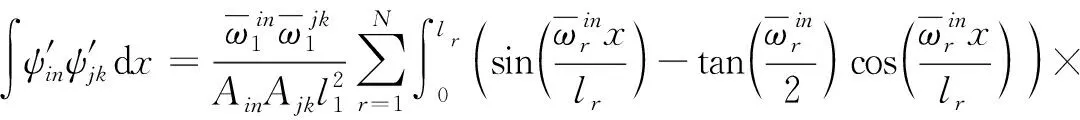
(33)
化简式(33)可得
(34)
将式(29)代入式(34)中,化简可得
(35)
利用模态叠加法求解连续方程需要用到式(35)的积分结果。
对于连续档导线中的每一档导线非线性振动方程均可描述为
(36)
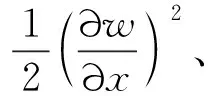
(37)
式中:N为指连续档的档数;φin(x)为单位正交模态,其中φin(x)=Binψin,当n为奇数时Bin可表示为
(38)
将式(37)代入式(36),在等式两边乘以φin(x)并在连续档长度范围内进行积分,可以获得主坐标形式下的非线性常微分方程
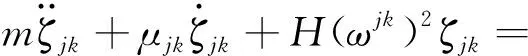
(39)

(40)
(41)
(42)
(43)
式(39)是一个非常有用的方程,该方程将连续档导线视为整体结构,通过这个方程可以分析连续档导线不同档之间、不同模态之间的耦合振动行为。
2.5 三档导线舞动分析
下面对一个简单问题进行分析,说明式(39)的应用价值。如研究考虑邻档导线影响的输电线舞动临界风速,可建立力学模型,如图16所示。只有跨越档2满足舞动条件,两边耐张档不满足舞动条件,即在跨越档2施加风载荷。现有舞动理论(有限元方法除外)一般不考虑相邻档导线的影响或者将相邻档导线等效为弹簧约束。
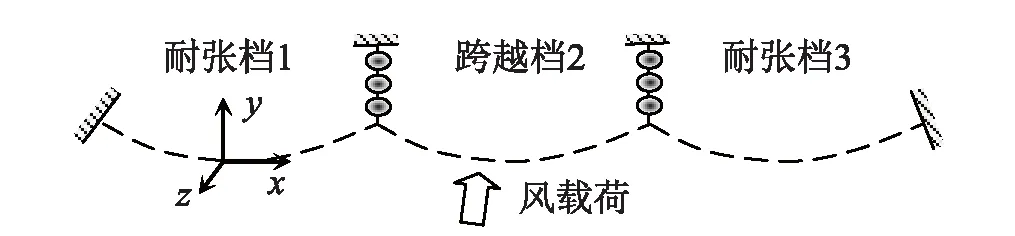
图16 三档覆冰导线模型Fig.16 Iced conductors model of three spans
只研究面内振动时,考虑风荷载影响的导线面内振动方程为
(44)
式中:U为风速;ρ为空气密度;d为裸导线直径;a1,a2均为气动参数。假设舞动激励φin(x)模态,则方程线性化后两边都乘φin(x)并沿长度范围积分可得
(45)
考虑到阻尼c由式(46)确定
(46)
则由式(46)可以确定考虑相邻档导线影响的覆冰导线舞动的临界风速
(47)
从式(47)可知,在相同阻尼比的情况下考虑邻档导线影响时频率ωin减少,降低了临界风速。对比图10所示的三个对称模态,舞动模式分别为ψ11,ψ21和ψ31时有不同的振动形式,而根据式(47)可知,不同的舞动模式可以影响临界风速的大小。
3 结 论
本文将多跨输电线分解为多个子结构即单档导线,结合现有的单跨索振动理论获得多跨输电线振动频率的理论公式,同时依据子结构理论获得了多跨输电线模态的理论公式。对本文获得的理论公式进行分析可以获得以下有意义的结论:
(1)绝缘子串的长度与导线张力对多跨输电线模态及频率有重要影响,当绝缘子串长度及导线张力较小的情况下多跨输电线可能表现出混合模态,不同于孤立档导线。
(2)多跨输电线的模态表明各档导线之间相互影响,可以推断当某档导线振动时会导致其它档导线振动,所以将多跨输电线简化为单档导线可能会导致错误的结论。
(3)多跨输电线产生共振的条件和单档导线产生共振的条件不相同,不能采用单跨索理论分析多档导线的共振,最后利用本文提出的理论模态将连续体振动的偏微分方程转换为常微分方程。
(4)首次给出舞动临界风速的理论计算公式,并从理论上阐述了考虑相邻档导线影响的覆冰输电线舞动临界风速大于孤立档导线,并指出临界风速的大小还与激励的多跨输电线振动模态有关。
通过本文提供的理论方法可以计算出多档导线的振动频率及模态,依据获得的理论公式可以确定导线产生内共振的条件,从获得的模态函数可以对连续系统进行解耦分析,本文所取得的研究成果对于研究多档导线的动力响应具有理论价值。
